U4_2:图论之MST/Prim/Kruskal
文章目录
- 一、最小生成树-MST
- 生成MST策略
- 一些定义
- 思路
- 彩蛋
- 二、普里姆算法(Prim算法)
- 思路
- 算法流程
- 数据存储
- 分析
- 伪代码
- 时间复杂度分析
- 三、克鲁斯卡尔算法(Kruskal算法)
- 分析
- 算法流程
- 并查集-Find-set
- 伪代码
- 时间复杂度分析
一、最小生成树-MST
无向图,无环,所有点连通,边权重和最小
(没有权重标注就默认为1)
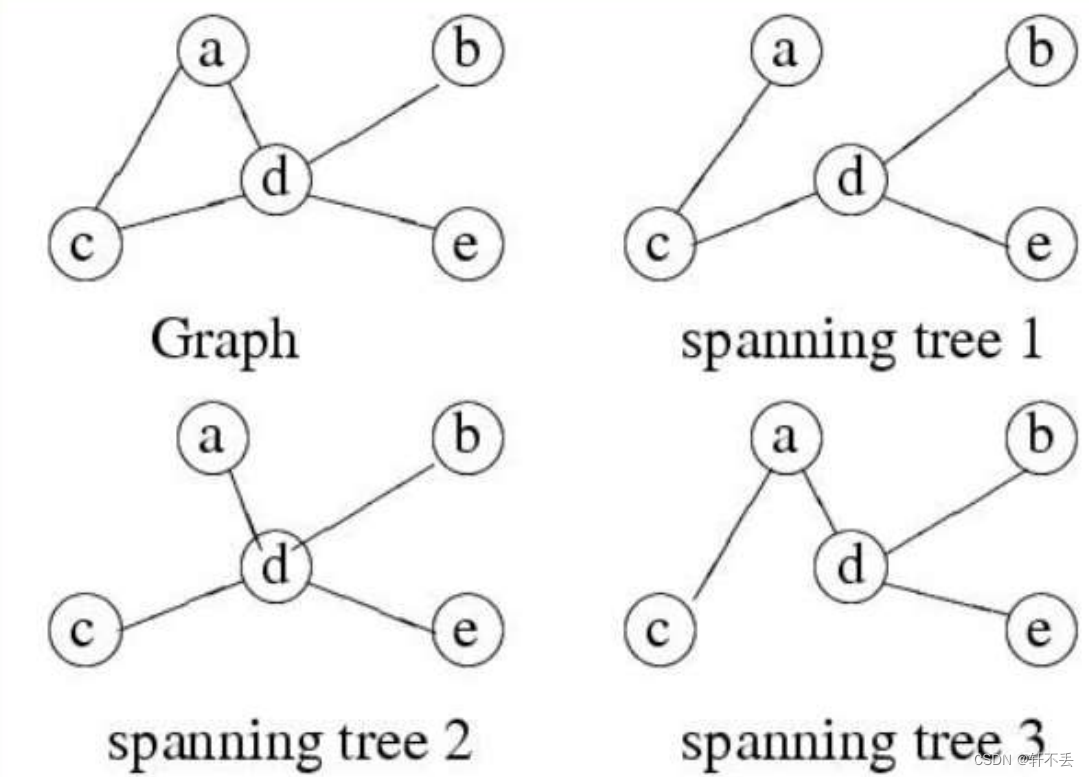
生成MST策略
- 从一个空图开始。
- 尝试一次添加一条边,始终确保所构建的保持无循环。
- 如果在添加了每条边之后,我们确定生成的图是某个最小生成树的子集,我们就完成了。
一些定义
集合 A A A是最小生成树 T T T的子集,当 A U ( u , v ) A\space U(u,v) A U(u,v)也是 M S T MST MST子集时, ( u , v ) (u,v) (u,v)是安全的。
切割 c u t cut cut: ( S , V − S ) (S,V-S) (S,V−S)
a a a c u t cut cut r e s p e c t s respects respects a a a s e t set set A A A o f of of e d g e s edges edges i f if if n o no no e d g e s edges edges i n in in A A A c r o s s e s crosses crosses t h e the the c u t cut cut.
An edge is a light edge crossing a cut if its weight is the minimumof any edge crossing the cut
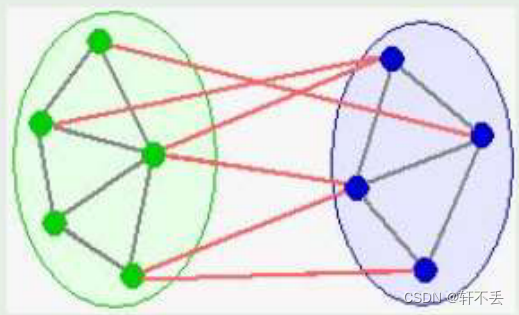
思路
(S, V - S) be any cut of G that respects A
(u, v) be a light edge crossing the cut (S, V - S)Then, edge (u, v) is safe for A.
则 lt means that we can find a safe edge by
- first finding a cut that respects A
- then finding the light edge crossingthat cut
That light edge is a safe edge
彩蛋
本质上下面所要讲的Prim算法和Kruskal算法都是依据这个总思路来的,先分隔cut,然后根据cut找light edge,最后不断生成MST
二、普里姆算法(Prim算法)
思路
- 首先选择任意顶点r作为树的根。
- 当树不包含图中的所有顶点时:找到离开树的最短边并将其添加到树中。
这个思路可以想到,每次的cut就是选入作为顶点的集合 S S S和未选入的顶点 G − S G-S G−S
算法流程
数据存储
区分cut:最初始是空集,所有顶点被标记为白色,选入的顶点标记为黑色
利用优先队列存储
利用优先队列(小顶堆)去寻找 t h e the the l i g h e s t lighest lighest e d g e edge edge(相应函数如下)
3. I n s e r t ( u , k e y ) Insert(u, key) Insert(u,key):用键值key在Q中插入u。
4. u = E x t r a c t − m i n ( ) u = Extract- min() u=Extract−min():提取键值最小的项。
5. D e c r e a s e − K e y ( u , n e w − k e y ) Decrease-Key(u, new-key) Decrease−Key(u,new−key):将u的键值减小为new-key
利用 p r e d [ A ] pred[A] pred[A]去存储每个顶点的存储顺序
分析
t h e the the l i g h e s t lighest lighest e d g e edge edge本质上是在黑白分界点的这些边中寻找,因此每次更新都需要维护这些点( k e y key key)。
初始的时候设为 i n i f i n i t y inifinity inifinity,每次加入新顶点时就找到它的所有边判断是否比现在的key是否更小了,如果更小了就可以更新并且换前驱
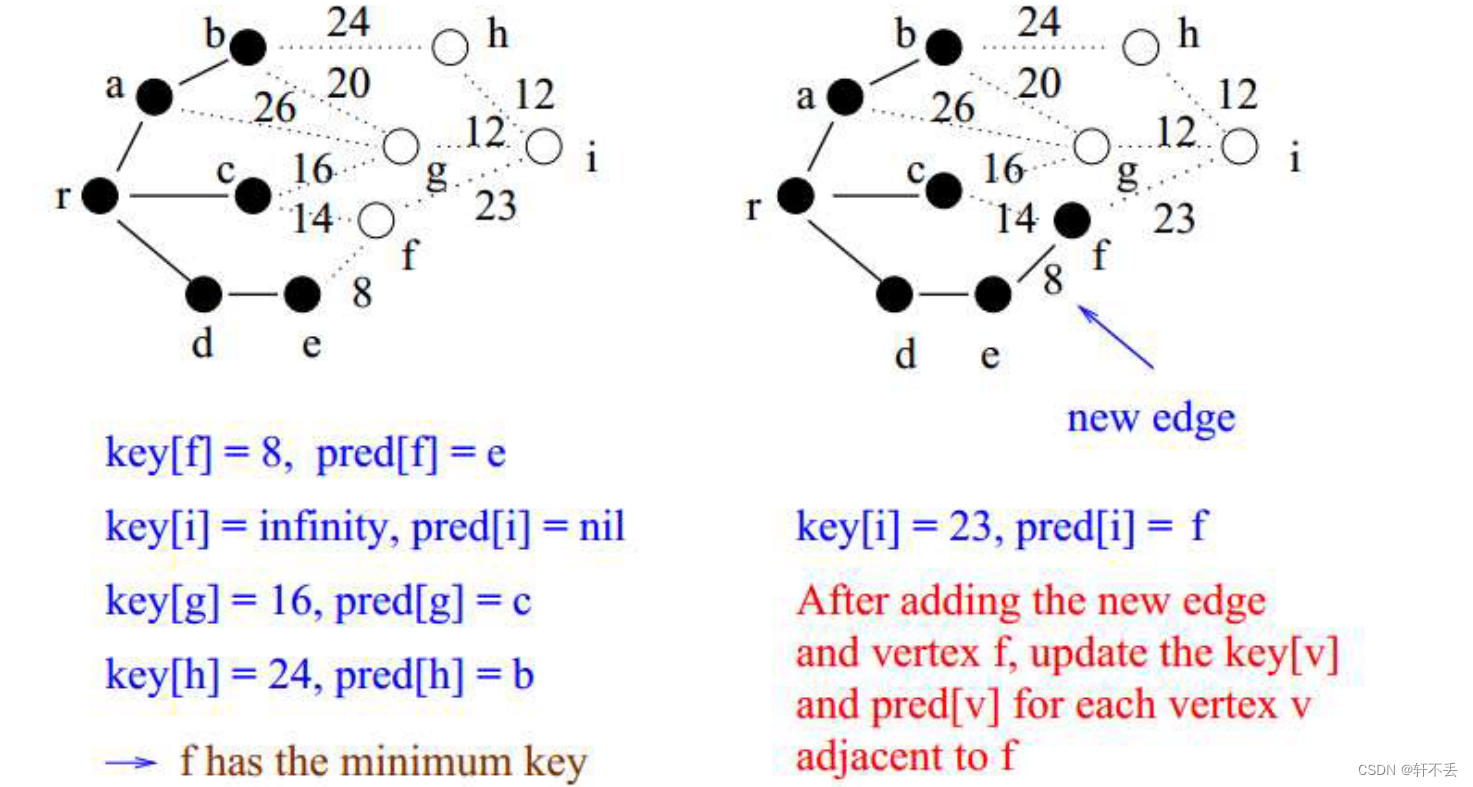
伪代码
for u ∈ V docolor[u] ← white,key[u] ← +∞
end
key[u] ← 0,pred[r] ← null; //最开始的顶点
Q ← new PriQueue(V)
while Q is noempty dou ← Q.Extract-Min(); //the lighest edge for v ∈ adj[u] doif(color[u] ← white && w[u,v] < key[u]) thenkey[u] ← w[u,v]Q.decrease-Key(v,key[u]) pred[v] ← uendendcolor[u] ← black
end
时间复杂度分析
创建优先队列 O ( V l o g V ) O(VlogV) O(VlogV),每次循环 E x t r a c t − M i n Extract-Min Extract−Min为 l o g ( V ) log(V) log(V),总共V个顶点,总时间复杂度为 O ( V l o g V ) O(VlogV) O(VlogV)。每次循环 D e c r e a s e − K e y Decrease-Key Decrease−Key为 O ( l o g V ) O(logV) O(logV),因为循环内每次更新都是针对边来说,所有边都遍历一遍,因此循环内总时间复杂度为 O ( E l o g V ) O(ElogV) O(ElogV),总时间复杂度为 T ( n ) = O ( ( V + E ) l o g V ) = O ( E l o g V ) T(n)=O((V+E)logV)=O(ElogV) T(n)=O((V+E)logV)=O(ElogV)
三、克鲁斯卡尔算法(Kruskal算法)
分析
- 从一个空图开始。
- 尝试一次添加一条边,始终确保所构建的保持无循环。.
- 如果我们在每一步都确定生成的图是某个最小生成树的子集,我们就完成了。
与Prim的算法生长一棵树不同,Kruskal的算法生长一组树(森林)。
最初,这个森林只由顶点组成(没有边)。
在每一步中,添加不产生循环的权重最小的边。
继续直到森林“合并”成一棵树。
本质上,也是继承于一说的主算法:
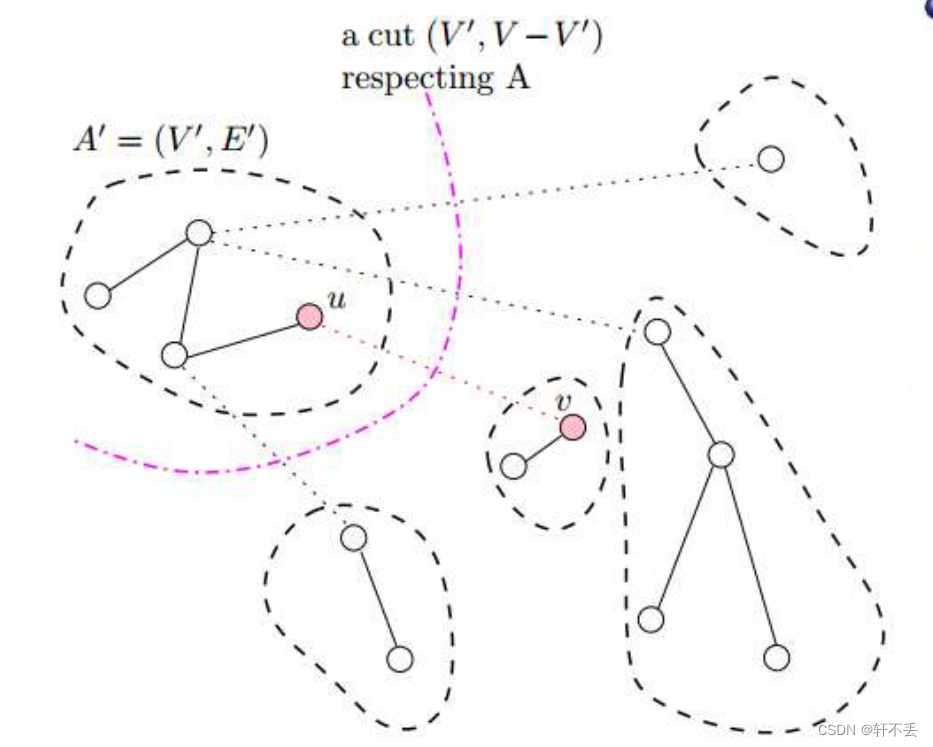
设A为Kruskal算法选择的边集,设(u, v)为下一步要添加的边。这足以说明这一点:
t h e r e there there i s is is a a a c u t cut cut t h a t that that r e s p e c t s respects respects A A A
( u , v ) (u, v) (u,v) i s is is t h e the the l i g h t light light e d g e edge edge c r o s s i n g crossing crossing t h i s this this c u t cut cut
算法流程
- 刚开始 A A A为空集, F F F存入所有边并且从小到大排序,
- 在F中选择一条权值最小的边e,检查将e加到A上是否形成一个循环。
构成循环,则从F移除
不构成循环,则从F添加进A - F为空集时停止操作
现在有个问题,怎么才能不形成环呢,
在框架算法的每一步中, ( V , A ) (V,A) (V,A)都是非循环的,因此它是一个森林,一个顶点延申两条枝干,且枝干之间没有路径,这样就是森林。因此:
如果 u u u和 v v v在同一棵树中,则将边 u , v {u,v} u,v添加到A中创建一个循环。
如果 u u u和 v v v不在同一棵树中,那么将边 u , v {u,v} u,v添加到 A A A中不会创建一个循环。
根据这个性质,如果一条边被选中,它的两个端点若在一个树上,那么再将这条边添加进树时,肯定会形成环,根据这一性质,我们可以维护并查集去判断是否成环
并查集-Find-set
本质上,并查集就是一个个树集合,每个元素都唯一指向它的父亲,根节点父亲就是子集,因此每棵树的唯一标识就是根节点。如果两个元素唯一标识一样,那它们就在一棵树上。
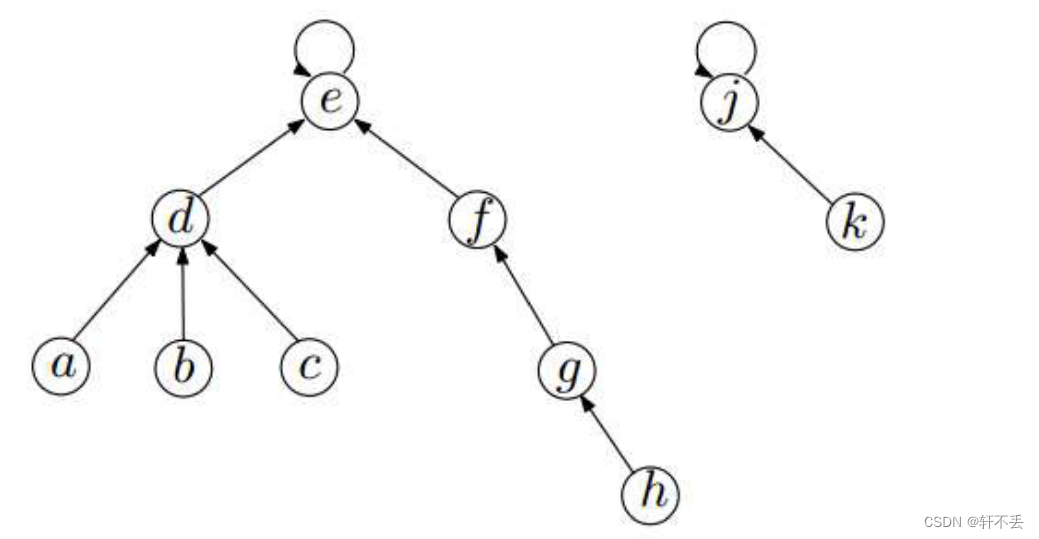
j u d g e judge judge f i n d − s e t ( u ) find-set(u) find−set(u) = = == == f i n d − s e t ( v ) find-set(v) find−set(v),维护 f i n d − s e t find-set find−set过程如下:
- C r e a t e − s e t u ) Create-set u) Create−setu):创建包含单个元素 u u u的集合。 O ( 1 ) O(1) O(1)
x.parent ← x
- F i n d − s e t ( u ) Find-set (u) Find−set(u):查找包含元素u的集合(假设每个集合都有唯一的ID,后面可知是树的根节点)。 O ( l o g n ) O(logn) O(logn)
while x != x.parent dox ← x.parent
end
- U n i o n ( u , v ) Union(u, v) Union(u,v):将分别包含u和v的集合归并为一个公共集合。(当判断完不会形成环后,可以合并). O ( l o g n ) O(logn) O(logn)(找树的根节点费时,其他都是 O ( 1 ) O(1) O(1)时间)
注意当我们将两棵树合并在一起时,我们总是将高树的根作为矮树的父树。不然会很畸形,费时。
如果两棵树有相同的高度,我们选择第一棵树的根指向第二棵树的根。树的高度增加了1(根节点+被合并的子树,因此高度+1)。其他情况下树的高度都是不变的。
a ← Find-Set(x)
b ← Find-Set(y)
if a.height <= b.height thenif a.height is equal to b.height thenb.hright++;enda.parent ← b
end
elseb.parent ← a
end
伪代码
sort E in increasing order by weight w;
A ← {}
for u ∈ V doCreate-Set(u);
end
for ei ∈E do //ei两个端点为ui,viif(find-set(ui)!=find-set(vi)) thenadd {ui,vi} to AUnion(ui,vi)end
end
return
时间复杂度分析
排序用时 O ( E l o g E ) O(ElogE) O(ElogE), c r e a t e − s e t create-set create−set用时 O ( V ) O(V) O(V),循环次数是边的次数 E E E,每次循环 u n i o n union union花费 l o g ( V ) log(V) log(V),总时间复杂度 O ( E l o g V ) O(ElogV) O(ElogV),因此总花费 T ( n ) = O ( E l o g E ) T(n)=O(ElogE) T(n)=O(ElogE)(边比顶点多,取大的)
相关文章:

U4_2:图论之MST/Prim/Kruskal
文章目录 一、最小生成树-MST生成MST策略一些定义 思路彩蛋 二、普里姆算法(Prim算法)思路算法流程数据存储分析 伪代码时间复杂度分析 三、克鲁斯卡尔算法(Kruskal算法)分析算法流程并查集-Find-set 伪代码时间复杂度分析 一、最…...

springboot 注解@JsonInclude
修饰 实体属性or实体类 //枚举值:ALWAYS,NON_NULL,NON_ABSENT,NON_EMPTY,NON_DEFAULT,CUSTOM,USE_DEFAULTS JsonInclude(Include.NON_EMPTY)//将该标记放在属性上,如果该属性为NULL则不参与序列化 //如果放在类上边,那对这个类的全部属性起作用 Inclu…...

Python 中文完整教程目录
Python 教程 Python 是一门易于学习、功能强大的编程语言。它提供了高效的高级数据结构,还能简单有效地面向对象编程。Python 优雅的语法和动态类型以及解释型语言的本质,使它成为多数平台上写脚本和快速开发应用的理想语言。 Python 官网(…...

C/C++---------------LeetCode第35. 搜索插入位置
插入的位置 题目及要求二分查找在main内使用 题目及要求 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: …...

网络安全--基于Kali的网络扫描基础技术
文章目录 1. 标准ICMP扫描1.1使用Ping命令1.1.1格式1.1.2实战 1.2使用Nmap工具1.2.1格式1.2.2实战1.2.2.1主机在线1.2.2.2主机不在线 1.3使用Fping命令1.3.1格式1.3.2实战 2. 时间戳查询扫描2.1格式2.2实战 3. 地址掩码查询扫描3.1格式3.2实战 2. TCP扫描2.1TCP工作机制2.2TCP …...
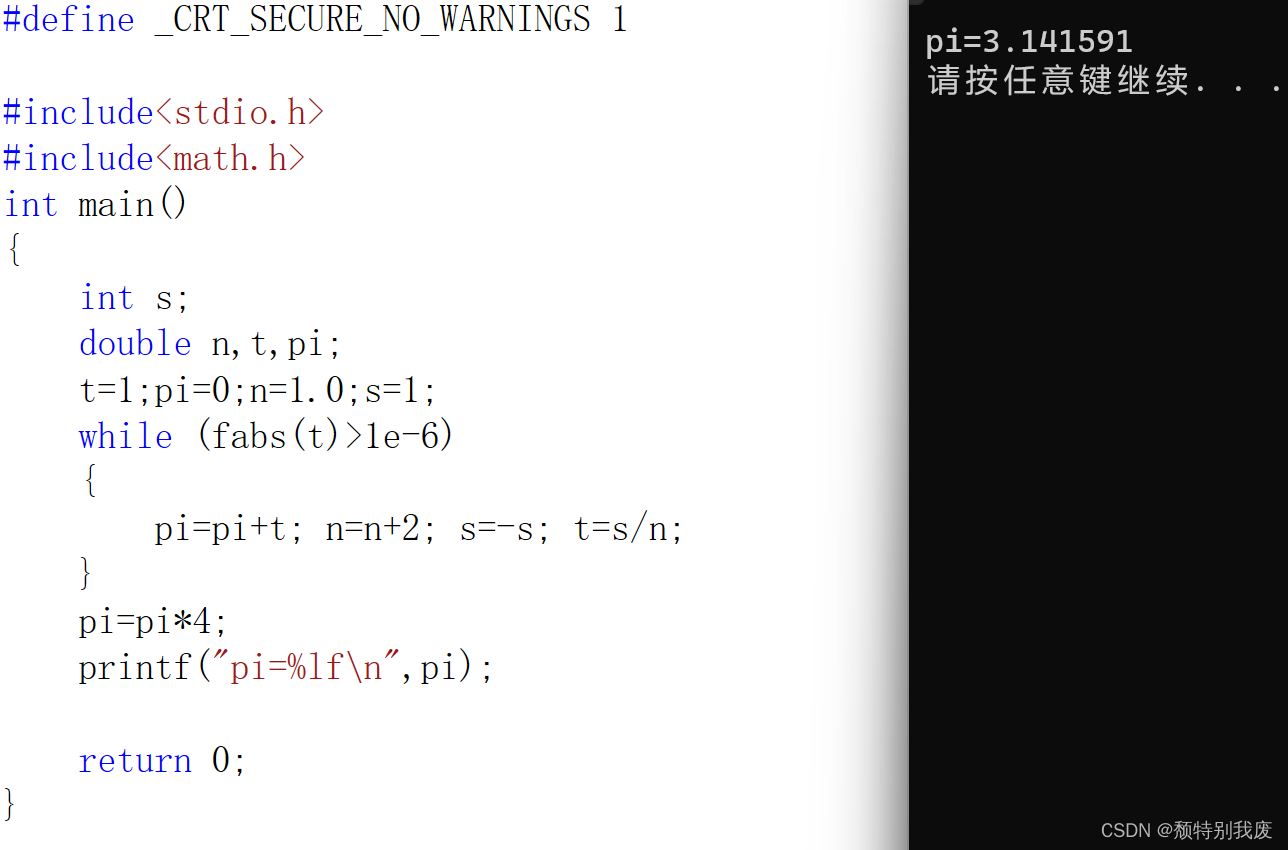
C语言——求π的近似值
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> #include<math.h> int main() {int s;double n,t,pi;t1;pi0;n1.0;s1;while (fabs(t)>1e-6){pipit; nn2; s-s; ts/n;}pipi*4;printf("pi%lf\n",pi);return 0; }这里是求小数点后6位——1e-6&#…...

如何使用ffmpeg转换图片格式
ffmpeg简介与图片格式介绍 windows安装ffmpeg,从如下网站下载release版本 https://www.gyan.dev/ffmpeg/builds/ ffmpeg 6.1版本仍然不支持heic的图片格式,未来可能会支持,具体见该issue: https://trac.ffmpeg.org/ticket/6521 …...

11 动态规划解最后一块石头的重量II
来源:LeetCode第1049题 难度:中等 描述:有一堆石头,用证书数组stones表示,其中stones[i]表示第i块石头的重量,每一回合,从中选出任意两块石头,然后将他们放在一起粉碎,…...
|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II)
LeetCode算法题解(动态规划,股票买卖)|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II
一、LeetCode121. 买卖股票的最佳时机 题目链接:121. 买卖股票的最佳时机 题目描述: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

python实验3 石头剪刀布游戏
实验3:石头剪刀布游戏 一、实验目的二、知识要点图三、实验1. 石头剪刀布2. 实现大侠个人信息 一、实验目的 了解3类基本组合数据类型。理解列表概念并掌握Python中列表的使用。理解字典概念并掌握Python中字典的使用。运用jieba库进行中文分词并进行文本词频统计。…...

米贸搜|如何设置 Facebook 转换 API + 事件重复数据删除
Facebook Pixel 可让您跟踪用户在您网站上的行为、收集再营销受众并创建相似对象。如果 Facebook 像素实现正确,它将向 FB 机器学习算法提供相关信息。 FB ML 将使用像素数据向最有可能转化的人展示您的广告。 几年来,我们可以通过 JavaScript 代码、应…...

python每日一题——11滑动窗口最大值
题目 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。 示例 1: 输入:nums [1,3,-1,-3,5,3,6,7], k 3…...
【C++ 程序设计入门基础】- 第3节-循环结构01
目录 循环结构 一、for 语句 for 循环案例 输入一个整数n,输出1~n的所有整数。 编译运行,查看输出结果 编译调试 for 循环结构语义分析 二、beak 语句 三、continue 语句 案例1: 案例2: 案例3: 循环…...

人工智能原理复习--知识表示(一)
文章目录 上一篇知识概述命题逻辑谓词逻辑谓词逻辑的应用 下一篇 上一篇 人工智能原理复习–绪论 知识概述 知识就是人类认识自然界的精神产物,是人类进行智能活动的基础。 是经过加工的信息,包括事实、信念和启发式规则。 分类: 按作用可…...

网络运维与网络安全 学习笔记2023.11.28
网络运维与网络安全 学习笔记 第二十九天 今日目标 OSPF汇总之域间路由、OSPF汇总之外部路由、OSPF链路认证 OSPF安全认证之区域认证、OSPF虚链路 OSPF汇总指域间路由 项目背景 企业内网运行多区域的OSPF网络,在R1 上存在多个不稳定的链路 R1上的不稳定链路&a…...

Rust开发——数据对象的内存布局
枚举与Sized 数据 一般数据类型的布局是其大小(size)、对齐方式(align)及其字段的相对偏移量。 1. 枚举(Enum)的布局: 枚举类型在内存中的布局通常是由编译器来确定的。不同的编译器可能有不…...

mySQL踩坑记录
1.MYSQL Workbench-8.0.27.1出现"Exception: Current profile has no WMI enabled"错误的解决方法 MYSQL Workbench-8.0.27.1出现“Exception: Current profile has no WMI enabled“错误的解决方法_赛风扥的博客-CSDN博客 C:\Program Files\MySQL\MySQL Workbench …...
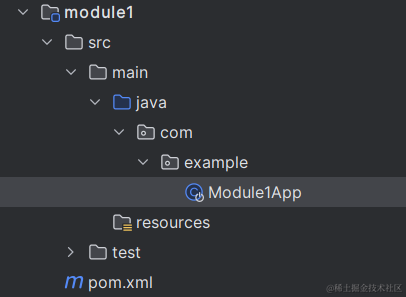
【Java】使用 IDEA 快速生成 SpringBoot 模块
项目目录下新建 module 模块 在 pom.xml 更改为 spring initializr 配置之后的 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchem…...

2023网络安全产业图谱
1. 前言 2023年7月10日,嘶吼安全产业研究院联合国家网络安全产业园区(通州园)正式发布《嘶吼2023网络安全产业图谱》。 嘶吼安全产业研究院根据当前网络安全发展规划与趋势发布《嘶吼2023网络安全产业图谱》调研,旨在进一步了解…...
一则 MongoDB 副本集迁移实操案例
文中详细阐述了通过全量 增量 Oplog 的迁移方式,完成一套副本集 MongoDB 迁移的全过程。 作者:张然,DBA 数据库技术爱好者~ 爱可生开源社区出品,原创内容未经授权不得随意使用,转载请联系小编并注明来源。 本文约 900…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
