算法中的时间复杂度,空间复杂度
一、前言
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别
衡量不同算法之间的优劣主要是通过时间和空间两个维度去考量:
- 时间维度:是指执行当前算法所消耗的时间,我们通常用「时间复杂度」来描述。
- 空间维度:是指执行当前算法需要占用多少内存空间,我们通常用「空间复杂度」来描述
通常会遇到一种情况,时间和空间维度不能够兼顾,需要在两者之间取得一个平衡点是我们需要考虑的
一个算法通常存在最好、平均、最坏三种情况,我们一般关注的是最坏情况
最坏情况是算法运行时间的上界,对于某些算法来说,最坏情况出现的比较频繁,也意味着平均情况和最坏情况一样差
二、时间复杂度
时间复杂度是指执行这个算法所需要的计算工作量,其复杂度反映了程序执行时间「随输入规模增长而增长的量级」,在很大程度上能很好地反映出算法的优劣与否
一个算法花费的时间与算法中语句的「执行次数成正比」,执行次数越多,花费的时间就越多
算法的复杂度通常用大O符号表述,定义为T(n) = O(f(n)),常见的时间复杂度有:O(1)常数型、O(log n)对数型、O(n)线性型、O(nlogn)线性对数型、O(n^2)平方型、O(n^3)立方型、O(n^k)k次方型、O(2^n)指数型,如下图所示:
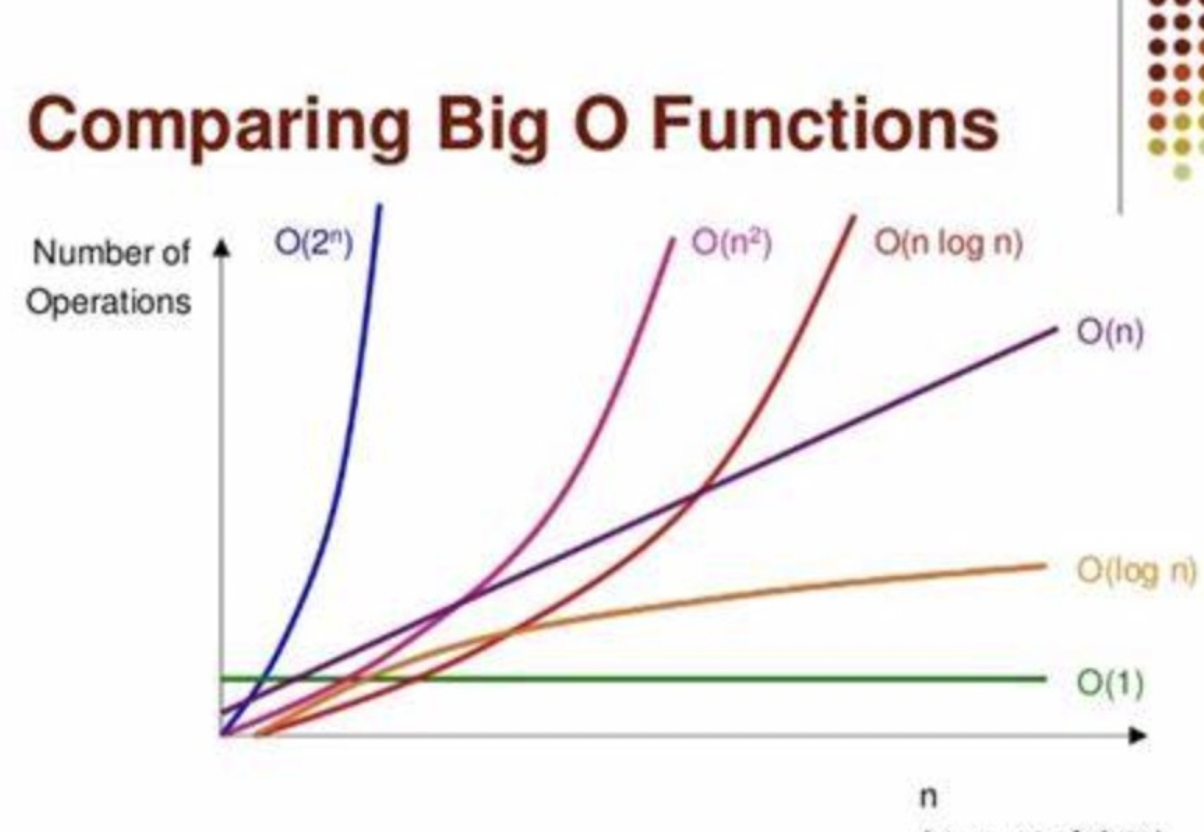
从上述可以看到,随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低,由小到大排序如下:
Ο(1)<Ο(log n)<Ο(n)<Ο(nlog n)<Ο(n2)<Ο(n3)<…<Ο(2^n)<Ο(n!)
注意的是,算法复杂度只是描述算法的增长趋势,并不能说一个算法一定比另外一个算法高效,如果常数项过大的时候也会导致算法的执行时间变长
关于如何计算时间复杂度,可以看看如下简单例子:
function process(n) {let a = 1let b = 2let sum = a + bfor(let i = 0; i < n; i++) {sum += i}return sum
}
该函数算法需要执行的运算次数用输入大小n的函数表示,即 T(n) = 2 + n + 1,那么时间复杂度为O(n + 3),又因为时间复杂度只关注最高数量级,且与之系数也没有关系,因此上述的时间复杂度为O(n)
又比如下面的例子:
function process(n) {let count = 0for(let i = 0; i < n; i++){for(let i = 0; i < n; i++){count += 1}}
}
循环里面嵌套循环,外面的循环执行一次,里面的循环执行n次,因此时间复杂度为 O(n*n*1 + 2) = O(n^2)
对于顺序执行的语句,总的时间复杂度等于其中最大的时间复杂度,如下:
function process(n) {let sum = 0for(let i = 0; i < n; i++) {sum += i}for(let i = 0; i < n; i++){for(let i = 0; i < n; i++){sum += 1}}return sum
}
上述第一部分复杂度为O(n),第二部分复杂度为O(n^2),总复杂度为max(O(n^2), O(n)) = O(n^2)
又如下一个例子:
function process(n) {let i = 1; // ①while (i <= n) {i = i * 2; // ②}
}
循环语句中以2的倍数来逼近n,每次都乘以2。如果用公式表示就是1 * 2 * 2 * 2 … * 2 <=n,也就是说2的x次方小于等于n时会执行循环体,记作2^x <= n,于是得出x<=logn
因此循环在执行logn次之后,便结束,因此时间复杂度为O(logn)
同理,如果一个O(n)循环里面嵌套O(logn)的循环,则时间复杂度为O(nlogn),像O(n^3)无非也就是嵌套了三层O(n)循环
三、空间复杂度
空间复杂度主要指执行算法所需内存的大小,用于对程序运行过程中所需要的临时存储空间的度量
除了需要存储空间、指令、常数、变量和输入数据外,还包括对数据进行操作的工作单元和存储计算所需信息的辅助空间
下面给出空间复杂度为O(1)的示例,如下
let a = 1
let b = 2
let c = 3
上述代码的临时空间不会随着n的变化而变化,因此空间复杂度为O(1)
let arr []
for(i=1; i<=n; ++i){arr.push(i)
}
上述可以看到,随着n的增加,数组的占用的内存空间越大
通常来说,只要算法不涉及到动态分配的空间,以及递归、栈所需的空间,空间复杂度通常为O(1),一个一维数组a[n],空间复杂度O(n),二维数组为O(n^2)
相关文章:

算法中的时间复杂度,空间复杂度
一、前言 算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别 衡量不同算法之间的优劣主要是通过时…...

Python基础:推导式(Comprehensions)详解
1. 推导式概念 Python推导式(comprehensions)是一种简洁而强大的语法,用于从已存在的数据(列表、元组、集合、字典等)中创建新的数据结构。推导式包括: 列表推导式元组推导式字典推导式集合推导式 2. 列表…...
安防监控视频融合平台EasyCVR定制化页面开发
安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。安防视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索…...
Roll-A-Ball 游戏
Roll-A-Ball 游戏 1)学习资料 b站视频教程:https://www.bilibili.com/video/BV18W411671S/文档: * Roll-A-Ball 教程(一), * Roll-A-Ball 教程(二)线上体验roll-a-ball成品 * http://www-personal.umich.e…...
医疗影像数据集—CT、X光、骨折、阿尔茨海默病MRI、肺部、肿瘤疾病等图像数据集
最近收集了一大波关于CT、X光等医疗方面的数据集包含骨折、阿尔茨海默病MRI、肺部疾病等类型的医疗影像数据,废话不多说,给大家逐一介绍!! 1、彩色预处理阿尔茨海默病MRI(磁共振成像)图像数据集 彩色预处理阿尔茨海默病MRI(磁共…...
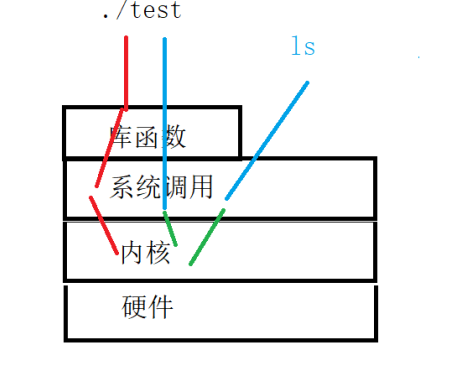
Linux僵死进程及文件操作
1.僵死进程(僵尸进程): 1.僵死进程产生的原因或者条件: 什么是僵死进程? 当子进程先于父进程结束,父进程没有获取子进程的退出码,此时子进程变成僵死进程. 简而言之,就是子进程先结束,并且父进程没有获取它的退出码; 那么僵死进程产生的原因或者条件就是:子进…...

用Python写一个浏览器集群框架
更多Python学习内容:ipengtao.com 在分布式爬虫和大规模数据采集的场景中,使用浏览器集群是一种有效的方式,可以提高数据采集的速度和效率。本文将介绍如何用Python编写一个简单但强大的浏览器集群框架,以应对需要使用多个浏览器实…...

【Github】git安装
我们经常需要对github上的项目进行复现或者使用,git指令可以方便我们更好地实现他们。 Part 0. 准备 配置代理IP 面对问题:关于登陆github网站网速慢、下载git项目网速慢。 解决:无论是windows还是linux系统,都可以找到/etc/ho…...
sql语法大全
1,创建数据库 create database 数据库名字; 2,查看所有的数据库名称 show databases; MySQL服务器已有4个数据库,这些数据库都是MySQL安装时自动创建的。 information_schema 和 performance_schema 数据库分别是 MySQL 服务器的数据字典(…...

小红书API接口测试 | 小红书笔记详情 API 接口测试指南
一、引言 随着互联网的发展,越来越多的应用开始使用API接口来提供服务。而API接口的测试也变得越来越重要。本文将介绍如何使用Python语言进行小红书笔记详情API接口的测试。 二、小红书笔记详情API接口介绍 小红书笔记详情API接口是用于获取指定笔记详细信息的接…...

实验六:Java流式编程与网络程序设计
一、字节输入/输出流实现数据的保存和读取 编程要求 根据提示,在右侧编辑器补充代码。 编写应用程序(SortArray.java),使用字节输入/输出流实现数据的保存和读取。 要求功能如下: 输入1~100之间的整型数据保存到数组…...

金字塔原理
金字塔原理 来自于麦肯锡公司的第一位女性咨询顾问芭芭拉•明托的著作《金字塔原理》。 原理介绍 此原理是一种重点突出、逻辑清晰、主次分明的逻辑思路、表达方式和规范动作。 金字塔的基本结构是:中心思想明确,结论先行,以上统下ÿ…...

VR全景技术助力政务服务大厅数字化,打造全新政务服务体验
引言: 随着科技的飞速发展,虚拟现实(VR)技术逐渐走进人们的视野。VR全景技术作为VR领域的一项重要应用,以其沉浸式、交互式的特点,正逐渐渗透到各行各业。政务服务大厅作为相关部门与民众之间的桥梁&#…...

使用Python实现SVM来解决二分类问题
下面是一个使用Python实现SVM来解决二分类问题的例子: # 导入所需的库 from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split from sklearn.svm import SVC import matplotlib.pyplot as plt# 生成一个二分类数据集 X, …...

合并PDF出现OOM异常
优化方法一:使用PdfSmartCopy类代替PdfCopy类。这个类可以在合并PDF文件时,检测并消除重复的对象,从而减少内存的占用。您可以参考以下代码示例: //创建一个Document对象 Document document new Document();//创建一个PdfSmartC…...

c语言-数据结构-链式二叉树
目录 1、二叉树的概念及结构 2、二叉树的遍历概念 2.1 二叉树的前序遍历 2.2 二叉树的中序遍历 2.3 二叉树的后序遍历 2.4 二叉树的层序遍历 3、创建一颗二叉树 4、递归方法实现二叉树前、中、后遍历 4.1 实现前序遍历 4.2 实现中序遍历 4.3 实现后序遍历 5、…...

DelayQueue介绍
5.1 DelayQueue介绍&应用 DelayQueue就是一个延迟队列,生产者写入一个消息,这个消息还有直接被消费的延迟时间。 需要让消息具有延迟的特性。 DelayQueue也是基于二叉堆结构实现的,甚至本事就是基于PriorityQueue实现的功能。二叉堆结构…...

centos8 redis 6.2.6源码安装+主从哨兵
文章目录 centos8 redis 6.2.6源码安装主从哨兵下载解压编译安装配置配置systemd服务启停及开机启动登录验证主从同步配置哨兵哨兵注册systemd centos8 redis 6.2.6源码安装主从哨兵 单机安装 下载解压 cd /data wget http://download.redis.io/releases/redis-6.2.6.tar.gz…...

机器学习之危险品车辆目标检测
危险品的运输涉及从离开仓库到由车辆运输到目的地的风险。监控事故、车辆运动动态以及车辆通过特定区域的频率对于监督车辆运输危险品的过程至关重要。 在线工具推荐: 三维数字孪生场景工具 - GLTF/GLB在线编辑器 - Three.js AI自动纹理化开发 - YOLO 虚幻合成数…...
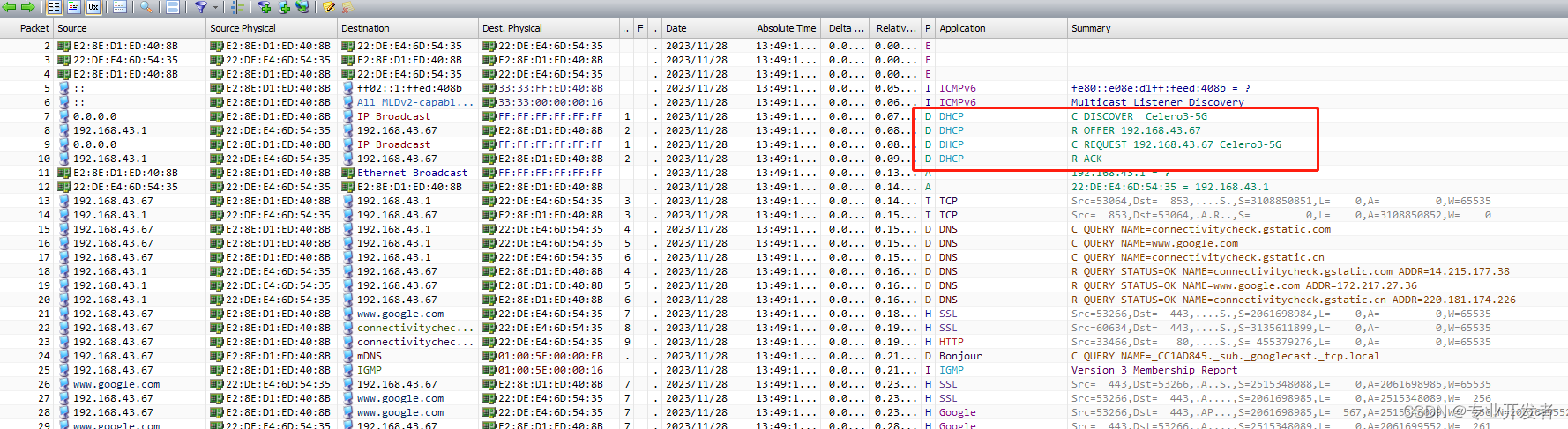
DHCP协议及实验omnipeek抓包工具分析 IPv4协议
一 抓包命令 adb shell tcpdump -i wlan0 -w /data/tcpdump.pcap 抓包后截图如下 二 DHCP是什么 2.1 DHCP定义 DHCP( Dynamic Host Configuration Protocol, 动态主机配置协议)定义: 存在于应用层(OSI) 前身是BOOTP(Bootstrap Protocol)协议 是一个使用UDP(User …...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...
