插入区间[中等]
优质博文:IT-BLOG-CN
一、题目
给你一个无重叠的 ,按照区间起始端点排序的区间列表。在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5]
输出:[[1,5],[6,9]]
示例 2:
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出:[[1,2],[3,10],[12,16]]
解释:这是因为新的区间[4,8]与[3,5],[6,7],[8,10]重叠。
示例 3:
输入:intervals = [], newInterval = [5,7]
输出:[[5,7]]
示例 4:
输入:intervals = [[1,5]], newInterval = [2,3]
输出:[[1,5]]
示例 5:
输入:intervals = [[1,5]], newInterval = [2,7]
输出:[[1,7]]
0 <= intervals.length <= 104
intervals[i].length == 2
0 <= intervals[i][0] <= intervals[i][1] <= 105
intervals根据intervals[i][0]按升序排列
newInterval.length == 2
0 <= newInterval[0] <= newInterval[1] <= 105
二、代码
对于区间S1=[l1,r1]和S2=[l2,r2]],如果它们之间没有重叠(没有交集),说明要么S1在S2的左侧,此时有r1<l2;要么S1在S2的右侧,此时有l1>r2。
如果r1<l2和l1>r2二者均不满足,说明S1和S2必定有交集,它们的交集即为[max(l1,l2),min(r1,r2)]并集即为[min(l1,l2),max(r1,r2)]
模拟: 在给定的区间集合X互不重叠的前提下,当我们需要插入一个新的区间S=[left,right]时,我们只需要:
【1】找出所有与区间S重叠的区间集合X′;
【2】将X′中的所有区间连带上区间S合并成一个大区间;
【3】最终的答案即为不与X′重叠的区间以及合并后的大区间;
这样做的正确性在于,给定的区间集合中任意两个区间都是没有交集的,因此所有需要合并的区间,就是所有与区间S重叠的区间。并且,在给定的区间集合已经按照左端点排序的前提下,所有与区间S重叠的区间在数组intervals中下标范围是连续的,因此我们可以对所有的区间进行一次遍历,就可以找到这个连续的下标范围。
当我们遍历到区间[li,ri]时:
【1】如果ri<left,说明[li,ri]与S不重叠并且在其左侧,我们可以直接将[li,ri]加入答案;
【2】如果li>right,说明[li,ri]与S不重叠并且在其右侧,我们可以直接将[li,ri]加入答案;
【3】如果上面两种情况均不满足,说明[li,ri]与S重叠,我们无需将[li,ri]加入答案。此时,我们需要将S与[li,ri]合并,即将S更新为其与[li,ri]的并集。
那么我们应当在什么时候将区间S加入答案呢?由于我们需要保证答案也是按照左端点排序的,因此当我们遇到第一个 满足li>right的区间时,说明以后遍历到的区间不会与S重叠,并且它们左端点一定会大于S的左端点。此时我们就可以将S加入答案。特别地,如果不存在这样的区间,我们需要在遍历结束后,将S加入答案。
class Solution {public int[][] insert(int[][] intervals, int[] newInterval) {int left = newInterval[0];int right = newInterval[1];boolean placed = false;List<int[]> ansList = new ArrayList<int[]>();for (int[] interval : intervals) {if (interval[0] > right) {// 在插入区间的右侧且无交集if (!placed) {ansList.add(new int[]{left, right});placed = true; }ansList.add(interval);} else if (interval[1] < left) {// 在插入区间的左侧且无交集ansList.add(interval);} else {// 与插入区间有交集,计算它们的并集left = Math.min(left, interval[0]);right = Math.max(right, interval[1]);}}if (!placed) {ansList.add(new int[]{left, right});}int[][] ans = new int[ansList.size()][2];for (int i = 0; i < ansList.size(); ++i) {ans[i] = ansList.get(i);}return ans;}
}
时间复杂度: O(n),其中n是数组intervals的长度,即给定的区间个数。
空间复杂度: O(1)。除了存储返回答案的空间以外,我们只需要额外的常数空间即可。
相关文章:

插入区间[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个无重叠的 ,按照区间起始端点排序的区间列表。在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。 示例 1&#x…...
Android Bitmap 模糊效果实现 (二)
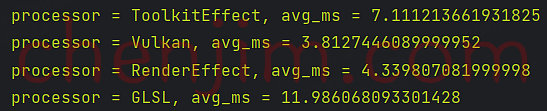
文章目录 Android Bitmap 模糊效果实现 (二)使用 Vukan 模糊使用 RenderEffect 模糊使用 GLSL 模糊RS、Vukan、RenderEffect、GLSL 效率对比 Android Bitmap 模糊效果实现 (二) 本文首发地址 https://blog.csdn.net/CSqingchen/article/details/134656140 最新更新地址 https:/…...

初识Java 18-4 泛型
目录 泛型存在的问题 在泛型中使用基本类型 实现参数化接口 类型转换和警告 无法实现的重载 基类会劫持接口 自限定类型 奇异递归类型 自限定 自限定提供的参数协变性 本笔记参考自: 《On Java 中文版》 泛型存在的问题 接下来讨论的,是在泛型…...

家政保洁预约小程序app开发特点有哪些?
家政预约服务小程序APP开发的特点介绍; 1. 低成本:用户通过手机APP下单,省去了中介费用,降低了雇主的雇佣成本。 2. 高收入:家政服务人员通过手机APP接单,省去了中介费用,从而提高了服务人员的…...

【JavaEE初阶】 HTTP响应报文
文章目录 🌲序言🎍200 OK🍀404 Not Found🎄403 Forbidden🌴405 Method Not Allowed🎋500 Internal Server Error🌳504 Gateway Timeout🌲302 Move temporarily🎍301 Move…...

PTA: 螺旋矩阵
题目 所谓“螺旋矩阵”,是指对任意给定的N,将1到NN的数字从左上角第1个格子开始,按顺时针螺旋方向顺序填入NN的方阵里。本题要求构造这样的螺旋方阵。 格式 输入格式: 输入在一行中给出一个正整数N(<10)。 输出…...
SparkSQL远程调试(IDEA)
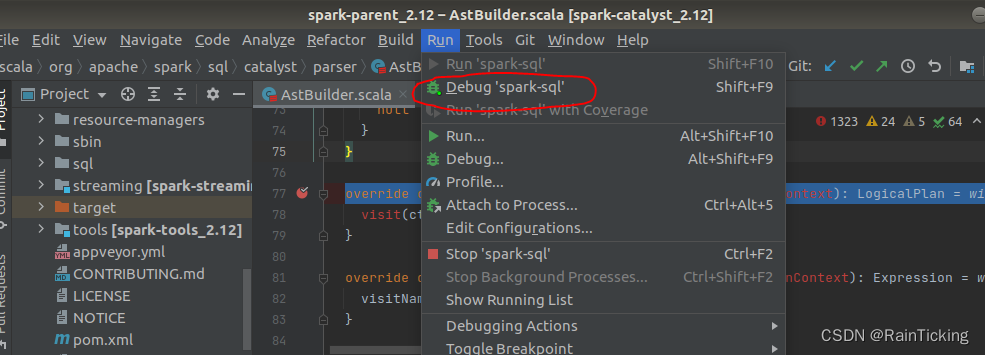
启动Intellij IDEA,打开spark源码项目,配置远程调试 Run->Edit Configuration 启动远程spark-sql spark-sql --verbose --driver-java-options "-Xdebug -Xrunjdwp:transportdt_socket,servery,suspendy,address5005"运行远程调试…...

Vue2 Vue3 响应式实现原理
Vue2 和 Vue3 的响应式实现原理有所不同。 Vue2 响应式实现原理: Vue2 使用 Object.defineProperty() 方法来实现数据劫持,从而实现数据的响应式更新。具体步骤如下: 首先,在初始化阶段,遍历 data 对象的所有属性&a…...

Android Tombstone 与Debuggerd 原理浅谈
一、前言 Android系统类问题主要有stability、performance、power、security。tombstoned是android平台的一个守护进程,它注册成3个socket服务端,客户端封装在crash_dump和debuggerd_client。 crash_dump用于跟踪定位C crash, debuggerd_cli…...

Matlab 三维电力线重建
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 之前曾经讨论过关于悬链线方程的曲线拟合点云最小二乘法拟合曲线,在这篇博客中其实拟合的是悬链线的一种近似形式,但对于大多数情况下已经够用了。方程如下所示: z = A ( x 2 + y 2 ) +...
GoLang Filepath.Walk遍历优化
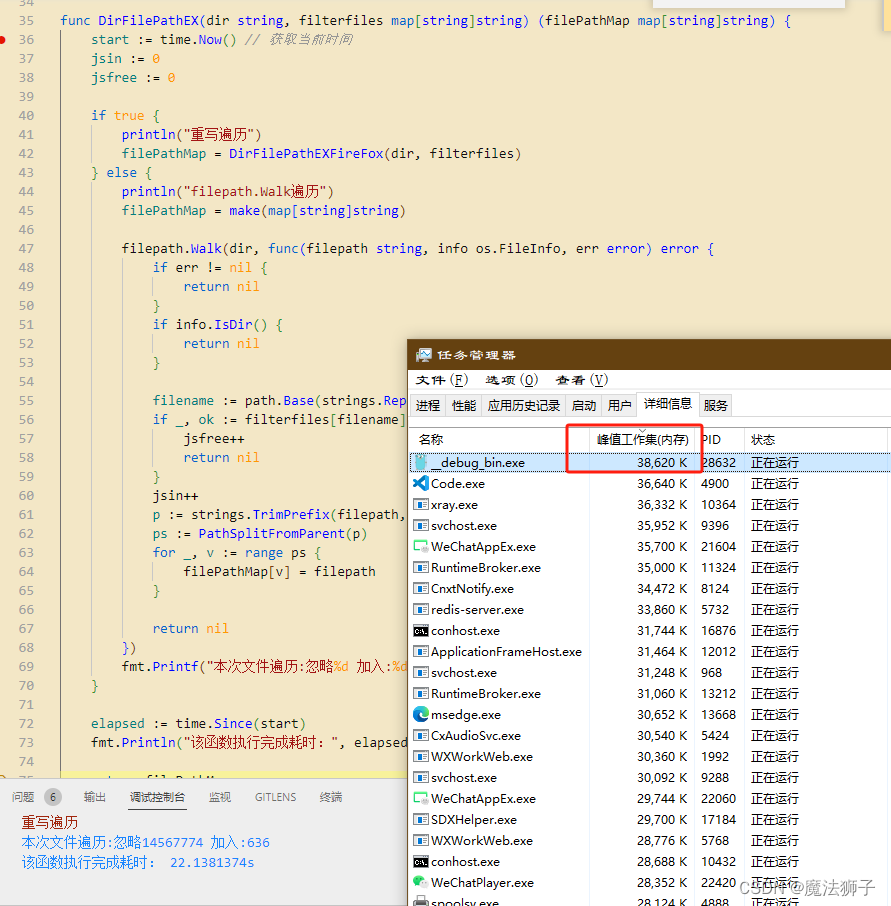
原生标准库在文件量过大时效率和内存均表现不好 1400万文件遍历Filepath.Walk 1400万文件重写直接调用windows api并处理细节 结论 1400万文件遍历时对比 对比条目filepath.walkwindows api并触发黑科技运行时间710秒22秒内存占用480M38M 关键代码 //超级快的文件遍历 fun…...

Java面向对象第7天
精华笔记: 成员内部类:了解,应用率不高 类中套类,外面的称为外部类,里面的称为内部类 内部类只服务于外部类,对外不具备可见性 内部类对象通常在外部类中创建 内部类中可以直接访问外部类的成员(包括私有…...

网络安全如何自学?
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

Flink-时间窗口
在流数据处理应用中,一个很重要、也很常见的操作就是窗口计算。所谓的“窗口”,一 般就是划定的一段时间范围,也就是“时间窗”;对在这范围内的数据进行处理,就是所谓的 窗口计算。所以窗口和时间往往是分不开的。 时…...
软件设计模式原则(三)单一职责原则
单一职责原则(SRP)又称单一功能原则。它规定一个类应该只有一个发生变化的原因。所谓职责是指类变化的原因。如果一个类有多于一个的动机被改变,那么这个类就具有多于一个的职责。而单一职责原则就是指一个类或者模块应该有且只有一个改变的原…...

使用Postman创建Mock Server
这篇文章将教会大家如何利用 Postman,通过 Mock 的方式测试我们的 API。 什么是 Mock Mock 是一项特殊的测试技巧,可以在没有依赖项的情况下进行单元测试。通常情况下,Mock 与其他方法的主要区别就是,用于取代代码依赖项的模拟对…...
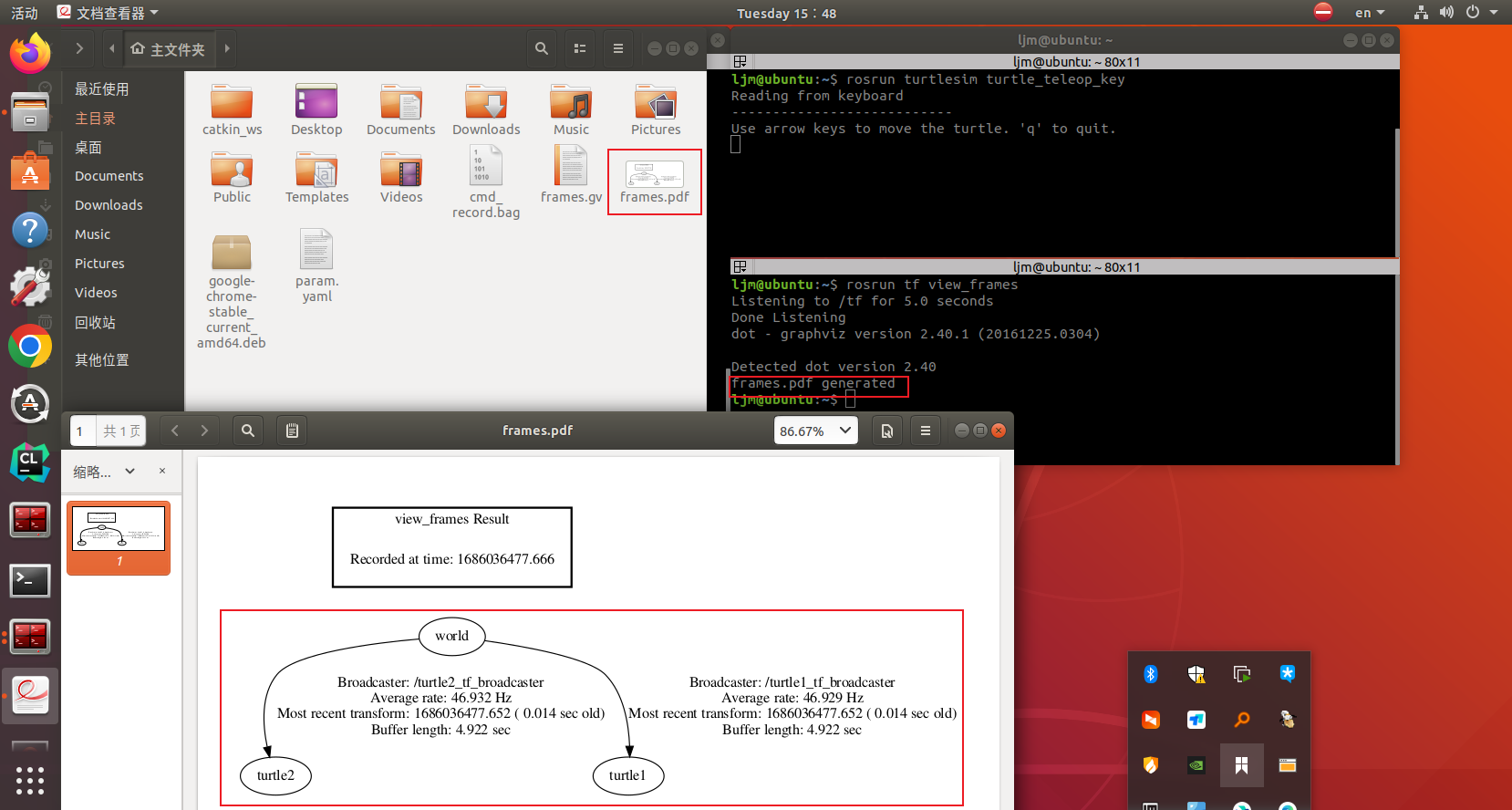
【古月居《ros入门21讲》学习笔记】15_ROS中的坐标系管理系统
目录 说明: 1. 机器人中的坐标变换 tf功能包能干什么? tf坐标变换如何实现 2. 小海龟跟随实验 安装 ros-melodic-turtle-tf 实验命令 运行效果 说明: 1. 本系列学习笔记基于B站:古月居《ROS入门21讲》课程,且使…...

初始linux:文件操作
目录 提示:以下指令均在Xshell 7 中进行 linux的理念 一、echo echo "字符串" 二、输出重定向 > > [文件] echo "字符串" > [文件] echo "字符串" > > [文件] 制作大文件 三、< 输入重定向与ca…...

iOS上传ipa使用可视化工具Transporter
文章目录 前言一、Transporter二、Appuploader三、iTMSTransporter总结 前言 最近为了让非开发人员上传IPA文件,特意找了一些方法,至于以前的ApplicationUploader已经不能用了,下面介绍两个工具可以上传IPA包。 一、Transporter 1、操作简单…...
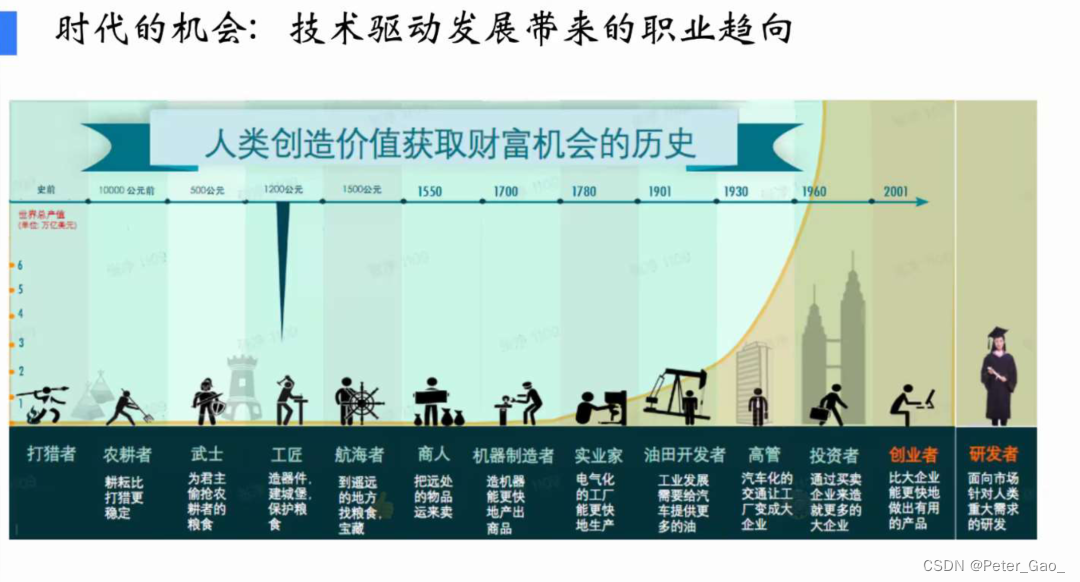
解读《陆奇最新演讲实录—我的大模型世界观》
腾讯科技频道记者张小珺一篇《陆奇最新演讲实录—我的大模型世界观》刷爆朋友圈。文章知识点丰富、字里行间处处流淌着创业方法论和AI应用商机,含金量极高! PS:一家之言、不求苟同。如有不爽之处,欢迎来 找我。 腾讯新闻原文&am…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
