数据结构与算法之递归: LeetCode 46. 全排列 (Typescript版)
全排列
- https://leetcode.cn/problems/permutations/
描述
- 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3
输入:nums = [1]
输出:[[1]]
提示
- 1 <= nums.length <= 6
- -10 <= nums[i] <= 10
- nums 中的所有整数 互不相同
算法实现
1 )回溯1: 基于数组
function permute(nums: number[]): number[][] {const res: number[][] = [];// 回溯函数const backtrack = (path: number[]) => {// 满足当前条件if(path.length === nums.length) {res.push(path);return;}// 遍历for(let i = 0; i < nums.length; i++) {if(path.includes(nums[i])) continue;backtrack(path.concat(nums[i]));}}backtrack([]);return res;
}
- 时间复杂度:O(n*n!)
- 假设输入数组的长度为 n
- 遍历每个元素的时间复杂度为 O(n)
- 对于每个元素,都会进行递归调,假设数组中有 n 个不同的元素
- 那么对于每个元素,都会有 n-1 个可能的选择,然后对于每个选择,又会有 n-2 个可能的选择,以此类推
- 因此,递归的时间复杂度可以表示为 O(n!)。
- 在每一层递归中,都会进行一次包含操作(includes),其时间复杂度为 O(n)。
- 综合考虑,这段代码的时间复杂度为 O(n * n!),其中 n 表示输入数组的长度。
- 需要注意的是,这里的时间复杂度分析基于平均情况。
- 在最坏情况下,全排列的数量是 n!,因此在最坏情况下,时间复杂度为 O(n * n!)
- 注意: n的阶乘公式:
n! = 1*2*3*...*(n-1)*n
- 空间复杂度:O(n)
- 递归,堆栈,不是常量,是线性增长的
- 是递归的层数
2 )回溯2: 基于交换
function permute(nums: number[]): number[][] {const res: number[][] = [];const backtrack = function(start: number) {if (start === nums.length - 1) {res.push([...nums]);return;}for (let i: number = start; i < nums.length; i++) {[nums[i], nums[start]] = [nums[start], nums[i]]; // 交换backtrack(start + 1); // 下一个数[nums[i], nums[start]] = [nums[start], nums[i]]; // 交换撤销}}backtrack(0); // 从 0 开始return res;
};
- 这个问题可以看作有 n 个排列成一行的空格,我们需要从左往右依此填入题目给定的 n 个数,每个数只能使用一次
- 那么很直接的可以想到一种穷举的算法,即从左往右每一个位置都依此尝试填入一个数
- 看能不能填完这 n 个空格,在程序中我们可以用「回溯法」来模拟这个过程
- 时间复杂度:O(n*n!),其中 n 为序列的长度
- 空间复杂度:O(n)
回溯算法、递归和深度优先遍历(DFS)之间存在密切的关系
-
它们通常在算法中一起使用,因为回溯算法通常使用递归来实现,并且常常涉及到深度优先遍历的思想。
-
回溯算法与递归
- 回溯算法是一种渐进式寻找并构建问题解决方案的策略。
- 在回溯算法中,通常通过递归的方式来尝试所有可能的情况。
- 当找到一个可能的解决方案时,它会继续探索下去,如果发现不符合条件,就会回溯到上一个状态,尝试其他可能的情况。
- 因此,回溯算法通常使用递归来实现,因为递归天然地适合于处理这种尝试所有可能情况的问题。
-
回溯算法与深度优先遍历
- 回溯算法通常使用深度优先遍历的思想。
- 在回溯算法中,我们会尝试一条路走到底,直到无法再继续下去,然后回溯到上一个状态,尝试其他的可能性。
- 这与深度优先遍历的思想是一致的,深度优先遍历也是尽可能深地搜索树的分支,直到无法再继续为止
- 然后回溯到上一个节点,继续搜索其他分支
-
因此,回溯算法通常使用递归来实现,并且其思想与深度优先遍历密切相关。
-
在许多情况下,回溯算法可以被视为一种特殊的深度优先遍历。
相关文章:
)
数据结构与算法之递归: LeetCode 46. 全排列 (Typescript版)
全排列 https://leetcode.cn/problems/permutations/ 描述 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,…...
、外连接(左外连接、右外连接、全外连接))
SQL中 JOIN 的两种连接类型:内连接(自然连接、自连接、交叉连接)、外连接(左外连接、右外连接、全外连接)
SQL中 JOIN 的两种连接类型:内连接(自然连接、自连接、交叉连接)、外连接(左外连接、右外连接、全外连接) 1. 自然连接(natural join)(内连接) 学生表 mysql> sele…...

微信小程序记住密码,让登录解放双手
密码是用户最重要的数据,也是系统最需要保护的数据,我们在登录的时候需要用账号密码请求登录接口,如果用户勾选记住密码,那么下一次登录时,我们需要将账号密码回填到输入框,用户可以直接登录系统。我们分别…...

国内划片机行业四大企业之博捷芯:技术驱动,领跑未来
在国内划片机行业中,公司以其卓越的技术实力和持续的创新精神,迅速崭露头角。作为国内划片机行业的四大企业之一,公司以其专业、高品质的划片机设备和解决方案,引领着行业的发展。 公司自创立以来,一直专注于划片机设备…...
后端整合Swagger+Knife4j接口文档
后端整合SwaggerKnife4j接口文档 接口文档介绍 什么是接口文档:写接口信息的文档,条接口包括: 请求参数响应参数 错误码 接口地址接口名称请求类型请求格式备注 为什么需要接口文档 who用?后端提供,前后端都需要使用…...
k8s中批量处理Pod应用的Job和CronJob控制器介绍
目录 一.Job控制器 1.简介 2.Jobs较完整解释 3.示例演示 4.注意:如上例的话,执行“kubectl delete -f myJob.yaml”就可以将job删掉 二.CronJob(简写为cj) 1.简介 2.CronJob较完整解释 3.案例演示 4.如上例的话…...
UE5 范围内随机生成
打开插件 BP_Actor...
杂记 | 使用Docker安装并配置MongoDB以支持事务(单副本,并解决了证书文件错误的问题)
文章目录 00 安装前的准备01 创建Docker Compose文件02 设置证书文件03 启动MongoDB04 初始化副本集和创建用户05 验证安装 00 安装前的准备 在开始之前,确保已经安装了Docker,本文基于Docker Compose进行示范,没有装Docker Compose也可将其…...

css三角,鼠标样式,溢出文字
目录 css三角 鼠标样式 例子:页码模块 溢出文字表示方式 margin负值运用 css三角强化 css三角 css三角中:line-height:0和font-size:0是防止兼容性的问题 jd {position: relative;width: 120px;height: 249px;background-…...
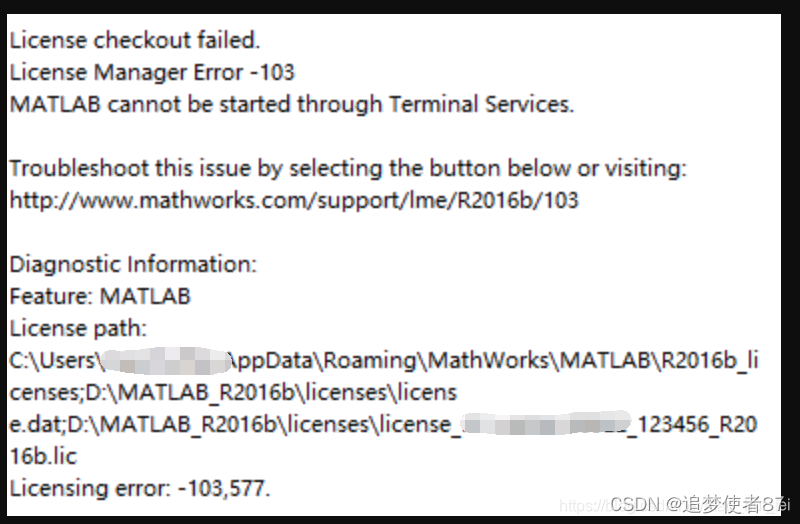
远程桌面访问MATLAB 2018B,提示License Manger Error -103,终极解决方案
通过远程桌面方位Windows Server系统下的MATLAB2018B,报错License Manger Error -103,Crack文件夹下的dll文件已经替换,同时也已经输出了lic文件,但是仍然无法打开。但是在本地桌面安装就没有问题。初步怀疑MATLAB的License使用机…...

Jmeter基础和概念
JMeter 介绍: 一个非常优秀的开源的性能测试工具。 优点:你用着用着就会发现它的重多优点,当然不足点也会呈现出来。 从性能工具的原理划分: Jmeter工具和其他性能工具在原理上完全一致,工具包含4个部分: …...

【Linux 带宽限速】trickle,限制docker 上传速度
限制docker 上传速度 然而,你可以使用第三方工具来实现这个目的。一个常用的工具是 trickle,它可以模拟网络带宽。 首先,你需要安装 trickle。在 Ubuntu 上,可以使用以下命令安装: sudo apt-get install trickle然后…...

MindStudio学习记录三:推理应用开发 acl mindx sdk
1.推理应用流程 1.1.创建工程 1.2.模型转换 1.3代码开发 1.3.1ACL代码 1.3.2MindX SDK开发 可视化模块化设计 中间的图片与处理 是基于AIPP的可视化处理 1.5.编译 交叉编译 1.6.运行与调试 1.7 调优工具 profiling性能分析 2.开发举例 resnet-50 2.1 准备工程 2.2.准备模型…...

【RT-DETR改进】SIoU、GIoU、CIoU、DIoU、AlphaIoU等二十余种损失函数
一、本文介绍 这篇文章介绍了RT-DETR的重大改进,特别是在损失函数方面的创新。它不仅包括了多种IoU损失函数的改进和变体,如SIoU、WIoU、GIoU、DIoU、EIOU、CIoU,还融合了“Alpha”思想,创造了一系列新的损失函数。这些组合形式的…...
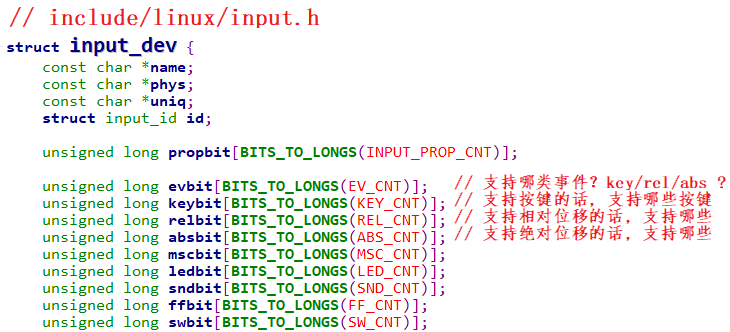
【Linux】EVIOCGBIT
EVIOCGBIT(ev, len) 该怎么理解? 我们可以推断出,它是一个宏,它的前两个参数已经确定了,具体的功能由后两个参数(ev,len)来决定。Linux-4.9.88\include\uapi\linux\input.h #define EVIOCGBIT(ev,len) _IOC(_IOC_READ, E, 0x20 …...
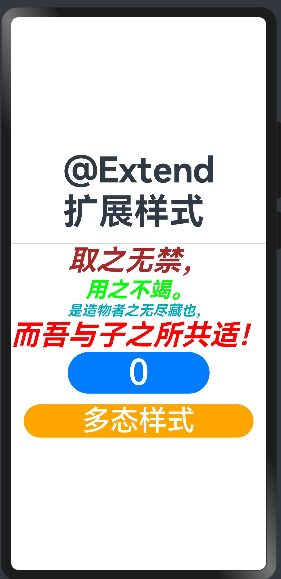
鸿蒙4.0开发笔记之ArkTS装饰器语法基础@Extend扩展组件样式与stateStyles多态样式(十一)
一、Extend扩展组件样式 1、作用 前文提到可以使用Styles用于样式的扩展,在Styles的基础上,ArkTS语法还提供了Extend,⽤于扩展原生组件样式,包括Text、Button等等。 2、定义语法 Extend(UIComponentName) function functionNam…...
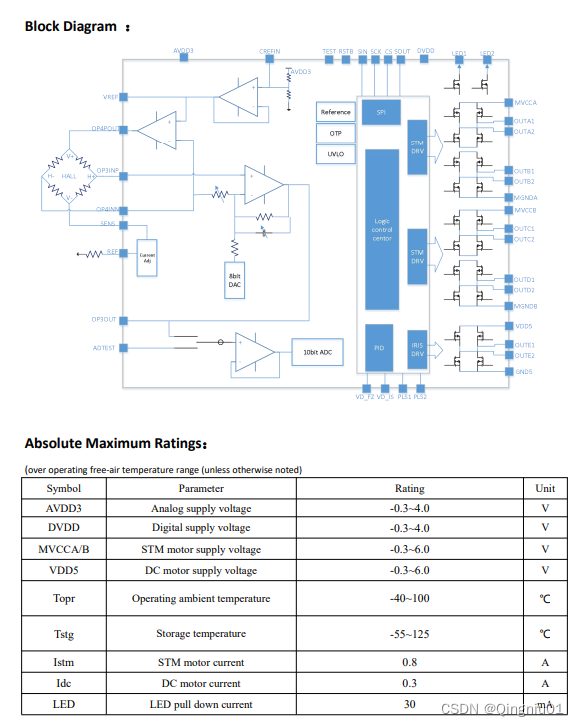
5V摄像机镜头驱动IC GC6208,可用于摄像机,机器人等产品中可替代AN41908
GC6208是一个镜头电机驱动IC摄像机和安全摄像机。该设备集成了一个直流电机驱动器的Iris的PID控制系统,也有两个通道的STM电机驱动器的变焦和对焦控制。 芯片的特点: 内置用于Iris控制器的直流电机驱动器 内置2个STM驱动程序,用于缩放和…...

PHP echo和print 语句
PHP 是通过 print 和 echo 语句来动态输出 HTML 内容,虽然 print 和 echo 语句两者的功能几乎是完全一样,但是还是有一点差别的。 在 PHP 中有两个基本的输出方式: echo 和 print。 本章节中我们会详细讨论两个语句的用法,并在实…...

ThinkPHP6.1 多应用模式的一些事儿
TP安装就不说了,直接从安装完成开始了。 安装多应用模式扩展 think-multi-app composer require topthink/think-multi-app删除 app 目录下的 controller 文件夹(TP 是根据是否有这个文件夹来判断单应用模式还是多应用模式的)。 创建应用 …...
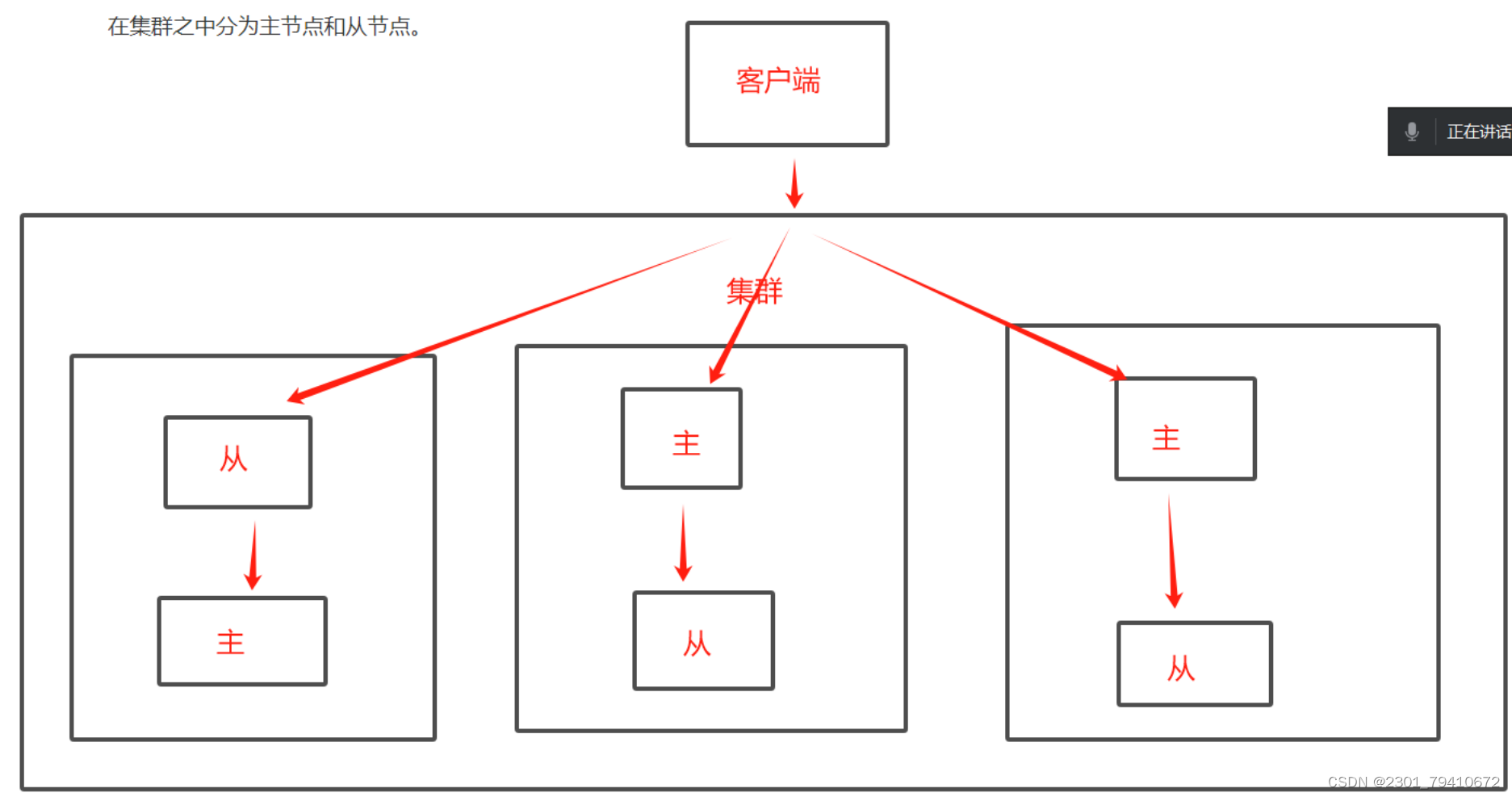
redis-cluster集群模式
Redis-cluster集群 1 Redis3.0引入的分布式存储方案 2集群由多个node节点组成,redis数据分布在节点之中,在集群之中分为主节点和从节点3集群模式当中,主从一一对应,数据写入和读取与主从模式一样,主负责写,从只能读4集群模式自带哨兵模式,可…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
