基于格攻击的密钥恢复方法
本篇博文介绍针对椭圆曲线签名算法的基于格攻击的密钥恢复方法,本研究将这种方法应用于椭圆曲线签名算法。针对椭圆曲线算法的攻击研究一般主要集中于算法的两个运算阶段,即标量乘阶段和组合阶段。对于椭圆曲线签名算法,针对标量乘阶段的攻击目标是恢复标量,即随机数的值。在只能获取随机数一部分比特信息的情况下,结合格基归约的方法仍然可以恢复密钥。这使得我们在攻击带有防护的算法实现时,可以考虑尝试恢复随机数一部分信息,而不是必须恢复完整的数值。这种使用格基归约的攻击方法称作格攻击,需要我们解决的问题就是如何将恢复密钥的问题归约到格上的最短向量问题。
签名算法密钥恢复问题的转化方法
格和隐数问题
给定一个素数 p p p, 记 ⌊ s ⌋ p \lfloor s \rfloor _p ⌊s⌋p 为 s s s 除以 p p p的模数,则隐数问题表述如下:给定若干数量随机选取的整数 t i ∈ F p t_i \in F_p ti∈Fp 和一个固定的未知整数 α \alpha α, 在二进制表示下已知 ⌊ α t i ⌋ p \lfloor \alpha t_i \rfloor _p ⌊αti⌋p的最高 l l l 比特信息,要求恢复 α \alpha α的值,整数 x ∈ F p x \in F_p x∈Fp的最高 l l l 比特信息记为 M S B l , p ( x ) MSB_{l,p}(x) MSBl,p(x).
定义1(格 (LATTICE)),设 R m R^m Rm是 m m m 维欧式空间,给定 n n n 个线性无关向量 b 1 , b 2 , . . . b n ∈ R m b_1,b_2,...b_n \in R^m b1,b2,...bn∈Rm,则由这些向量生成的格 L L L定义为这 n n n格向量的所有整数线性组合组成的集合。
L = { ∑ i = 1 n x i b i ∣ x i ∈ Z } L = \{\sum_{i=1}^{n}x_i b_i | x_i \in Z\} L={i=1∑nxibi∣xi∈Z}
这 n n n 个向量 { b 1 , b 2 , . . . b n ∈ R m } \{b_1,b_2,...b_n \in R^m\} {b1,b2,...bn∈Rm}设为格 L L L的一组基。如果以这 n n n 个列向量构成 m × n m \times n m×n 矩阵 B,则格 L L L同样可定义为矩阵 B B B 生成:
L ( B ) = { B x ∣ x ∈ Z n } = { v ∈ R n ∣ ( v ) = ∑ i = 1 n x i b i ∣ x i ∈ Z L(B) = \{Bx|x\in Z^n\}=\{v\in R^n|(v)=\sum_{i=1}^{n}x_i b_i | x_i \in Z L(B)={Bx∣x∈Zn}={v∈Rn∣(v)=i=1∑nxibi∣xi∈Z
当 m = n m=n m=n时,格 L L L称为满格。
最近向量问题是格中一个基本问题,其定义如下:给定格 L L L和一个目标向量 u ∈ R n u\in R^n u∈Rn 且 u u u不在个 L L L中,找到一个向量 v ∈ L v\in L v∈L,使得 u u u和 v v v之间的欧式距离 ∣ ∣ u − v ∣ ∣ ||u-v|| ∣∣u−v∣∣最小。
考虑隐数问题的一个实例:随机选取 t 1 , . . . t d t_1,...t_d t1,...td,并定义相应的最高 l l l 比特信息 u i = M S B l , p ( ⌊ α t i ⌋ p ) u_i=MSB_{l,p}(\lfloor \alpha t_i \rfloor _p) ui=MSBl,p(⌊αti⌋p).此时,给定 t 1 , . . . t d t_1,...t_d t1,...td, u 1 , . . . u d u_1,...u_d u1,...ud,以及 l l l 和 p p p,我们的目标是获取隐藏数值 α \alpha α。有, u i − ⌊ α t i ⌋ p ≤ p / 2 l + 1 u_i-\lfloor \alpha t_i \rfloor _p \leq p/2^{l+1} ui−⌊αti⌋p≤p/2l+1,这里包含了 d d d个不等式。此时,我们可以将这 d d d个不等式解释成是一个由 u i u_i ui构成的向量与另一个与 α \alpha α有关的向量之间的距离很小。引入一个由如下矩阵生成的格 L ( B ) L(B) L(B).
B = ( p 0 ⋯ 0 0 0 p ⋱ ⋮ ⋮ ⋮ ⋱ ⋱ 0 ⋮ 0 ⋯ 0 p 0 t 1 ⋯ ⋯ t d 1 / 2 l + 1 ) B = \begin{pmatrix} p & 0 & \cdots & 0 & 0 \\ 0 & p & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & p & 0\\ t_1 & \cdots & \cdots & t_d & 1/2^{l+1}\\ \end{pmatrix} B= p0⋮0t10p⋱⋯⋯⋯⋱⋱0⋯0⋮0ptd0⋮⋮01/2l+1
构建一个属于格 L ( B ) L(B) L(B)的行向量 y = ( ⌊ α t 1 ⌋ p , . . . ⌊ α t d ⌋ p , α / 2 l + 1 ) y =(\lfloor \alpha t_1 \rfloor _p ,...\lfloor \alpha t_d \rfloor _p ,\alpha/2^{l+1}) y=(⌊αt1⌋p,...⌊αtd⌋p,α/2l+1),显然,向量 y y y 与另一个属于格 L L L的行向量 u = ( u 1 , . . . u d , 0 ) u = (u_1,...u_d,0) u=(u1,...ud,0)之间的距离很近,即,满足
∣ ∣ y − u ∣ ∣ ∞ < p / 2 l + 1 ||y-u||_\infty < p/2^{l+1} ∣∣y−u∣∣∞<p/2l+1.
向量 y y y 暴露了 α \alpha α的信息,将其称作隐藏向量。
此时,我们向最近向量问题靠拢。
m i n { ∣ ∣ u − w ∣ ∣ ; w ∈ L ( B ) } ≤ d + 1 p / 2 l + 1 min \{||u-w||; w\in L(B)\} \leq \sqrt{d+1}p/2^{l+1} min{∣∣u−w∣∣;w∈L(B)}≤d+1p/2l+1
然后应用上述最近向量问题的描述,我们需要求解一个向量 v ∈ L ( B ) v \in L(B) v∈L(B),使得
∣ ∣ u − v ∣ ∣ ≤ 2 ( d + 1 ) / 4 m i n { ∣ ∣ u − w ∣ ∣ ; w ∈ L ( B ) } ≤ d + 1 2 ( d + 1 ) / 4 p / 2 l + 1 ||u-v||\leq 2^{(d+1)/4} min \{||u-w||; w\in L(B)\} \leq \sqrt{d+1} 2^{(d+1)/4} p/2^{l+1} ∣∣u−v∣∣≤2(d+1)/4min{∣∣u−w∣∣;w∈L(B)}≤d+12(d+1)/4p/2l+1
进而,我们得到格向量 y − v y-v y−v满足如下等式
∣ ∣ y − v ∣ ∣ ∞ ≤ ∣ ∣ y − u ∣ ∣ ∞ + ∣ ∣ u − v ∣ ∣ ≤ p ( 1 + d + 1 2 ( d + 1 ) / 4 ) 2 l + 1 ||y-v||_{\infty} \leq ||y-u||_{\infty}+||u-v||\leq \frac{p(1+\sqrt{d+1}2^{(d+1)/4})}{2^{l+1}} ∣∣y−v∣∣∞≤∣∣y−u∣∣∞+∣∣u−v∣∣≤2l+1p(1+d+12(d+1)/4)
当 l l l已知的最高比特位数和 d d d 不同 t i t_i ti的个数足够大时,向量 y − v y-v y−v很大概率是一个零向量。即我们通过解决最近向量问题得到的结果 v v v,在很大概率下就是我们所需要的隐藏向量 y y y。
SM2签名算法密钥恢复问题的转化
以SM2签名算法为例,把密钥签名私钥的问题归约到隐数问题。假设已知随机数 k k k的最低 l l l比特信息,定义这部分信息为 l s b l ( k ) lsb_l(k) lsbl(k),则 k = 2 l b + l s b l ( k ) k=2^l b + lsb_l(k) k=2lb+lsbl(k),其中 b b b是一个不小于0的整数(随机数)。显然, b < n / 2 l b < n/2^l b<n/2l。将等式带入到公式 s = ( k + r ) ( 1 + d A ) − 1 − r m o d n s = (k+r) (1+d_A)^{-1}-r \mod n s=(k+r)(1+dA)−1−rmodn,得到下式:
b = ( s + r ) 2 − l d A − ( l s b l ( k ) − s ) 2 − l m o d n b = (s+r)2^{-l}d_A-(lsb_l(k)-s)2^{-l} \mod n b=(s+r)2−ldA−(lsbl(k)−s)2−lmodn
定义 t = ⌊ ( s + r ) 2 − l ⌋ n t = \lfloor (s+r)2^{-l}\rfloor_n t=⌊(s+r)2−l⌋n 以及 u = ⌊ ( l s b l ( k ) − s ) 2 − l ⌋ n u= \lfloor(lsb_l(k)-s)2^{-l}\rfloor_n u=⌊(lsbl(k)−s)2−l⌋n,则等式简化为 b = d A t − u m o d n b=d_A t - u \mod n b=dAt−umodn。 ∣ x ∣ n |x|_n ∣x∣n表示将 x x x约减到 [ − n / 2 , n / 2 ) [-n/2,n/2) [−n/2,n/2)范围内,约减的方法是不断将 x x x减去 n n n,直到 x x x小于 n / 2 n/2 n/2。此时,由于 b ≤ n / 2 l b\leq n/2^l b≤n/2l,得到如下不等式。
0 ≤ ⌊ d A t − u ⌋ n ≤ n / 2 l 0 \leq \lfloor d_A t - u \rfloor _n \leq n/2^l 0≤⌊dAt−u⌋n≤n/2l
进而得到
∣ d A t − u − n / 2 l + 1 ∣ n ≤ n / 2 l + 1 | d_A t - u - n/2^{l+1}|_n \leq n/2^{l+1} ∣dAt−u−n/2l+1∣n≤n/2l+1
令 v = 2 l + 1 u + n v=2^{l+1}u+n v=2l+1u+n, 则得到
∣ d A t − v / 2 l + 1 ∣ n ≤ n / 2 l + 1 | d_A t - v/2^{l+1}|_n \leq n/2^{l+1} ∣dAt−v/2l+1∣n≤n/2l+1
根据隐数问题的定义,在这种条件下, v / 2 l + 1 v/2^{l+1} v/2l+1 即表示 ⌊ d A t ⌋ n \lfloor d_A t \rfloor _n ⌊dAt⌋n 的最高 l l l比特信息。现在给定 d d d组签名结果 ( r i , s i ) (r_i, s_i) (ri,si),计算每一组的 ( t i , v i ) (t_i,v_i) (ti,vi)。即,
t i = ⌊ ( s i + r i ) 2 − l ⌋ n t_i = \lfloor (s_i+r_i)2^{-l}\rfloor_n ti=⌊(si+ri)2−l⌋n
v i = 2 l + 1 ⌊ ( l s b l ( k ) − s ) 2 − l ⌋ n + n v_i = 2^{l+1}\lfloor(lsb_l(k)-s)2^{-l}\rfloor_n + n vi=2l+1⌊(lsbl(k)−s)2−l⌋n+n
满足:
∣ d A t i − v i / 2 l + 1 ∣ n ≤ n / 2 l + 1 | d_A t_i - v_i/2^{l+1}|_n \leq n/2^{l+1} ∣dAti−vi/2l+1∣n≤n/2l+1
构建一个 d + 1 d+1 d+1维的格 L ( B ′ ) L(B') L(B′),这个格由如下矩阵 B ′ B' B′生成:
B ′ = ( n 0 ⋯ 0 0 0 n ⋱ ⋮ ⋮ ⋮ ⋱ ⋱ 0 ⋮ 0 ⋯ 0 n 0 t 1 ⋯ ⋯ t d 1 / 2 l + 1 ) B'= \begin{pmatrix} n & 0 & \cdots & 0 & 0 \\ 0 & n & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & \cdots & 0 & n & 0\\ t_1 & \cdots & \cdots & t_d & 1/2^{l+1}\\ \end{pmatrix} B′= n0⋮0t10n⋱⋯⋯⋯⋱⋱0⋯0⋮0ntd0⋮⋮01/2l+1
隐藏向量 y = ( ⌊ d A t 1 ⌋ n , . . . ⌊ d A t d ⌋ n , d A / 2 l + 1 ) y = (\lfloor d_A t_1 \rfloor _n ,...\lfloor d_A t_d \rfloor _n ,d_A/2^{l+1}) y=(⌊dAt1⌋n,...⌊dAtd⌋n,dA/2l+1) 与向量 v = ( v 1 / 2 l + 1 , v 2 / 2 l + 1 , . . . , v d / 2 l + 1 , 0 ) v = (v_1/2^{l+1},v_2/2^{l+1},...,v_d/2^{l+1},0) v=(v1/2l+1,v2/2l+1,...,vd/2l+1,0)之间的距离很接近。因此可按上一节介绍的最近向量问题求解隐藏向量。
与SM2类似,由于随机数 k k k可以表示为 k = 2 l b + l s b l ( k ) k = 2^lb + lsb_l(k) k=2lb+lsbl(k),则有:
b = s − 1 r 2 − l d A − ( l s b l ( k ) − s − 1 z ) 2 − l m o d n b = s^{-1} r 2^{-l}d_A-(lsb_l(k)-s^{-1}z)2^{-l} \mod n b=s−1r2−ldA−(lsbl(k)−s−1z)2−lmodn
令 t = s − 1 r 2 − l t=s^{-1}r2^{-l} t=s−1r2−l以及 u = ( l s b l ( k ) − s − 1 z ) 2 − l u = (lsb_l(k)-s^{-1}z)2^{-l} u=(lsbl(k)−s−1z)2−l,后续推导同SM2类似,不做赘述。
相关文章:

基于格攻击的密钥恢复方法
本篇博文介绍针对椭圆曲线签名算法的基于格攻击的密钥恢复方法,本研究将这种方法应用于椭圆曲线签名算法。针对椭圆曲线算法的攻击研究一般主要集中于算法的两个运算阶段,即标量乘阶段和组合阶段。对于椭圆曲线签名算法,针对标量乘阶段的攻击…...
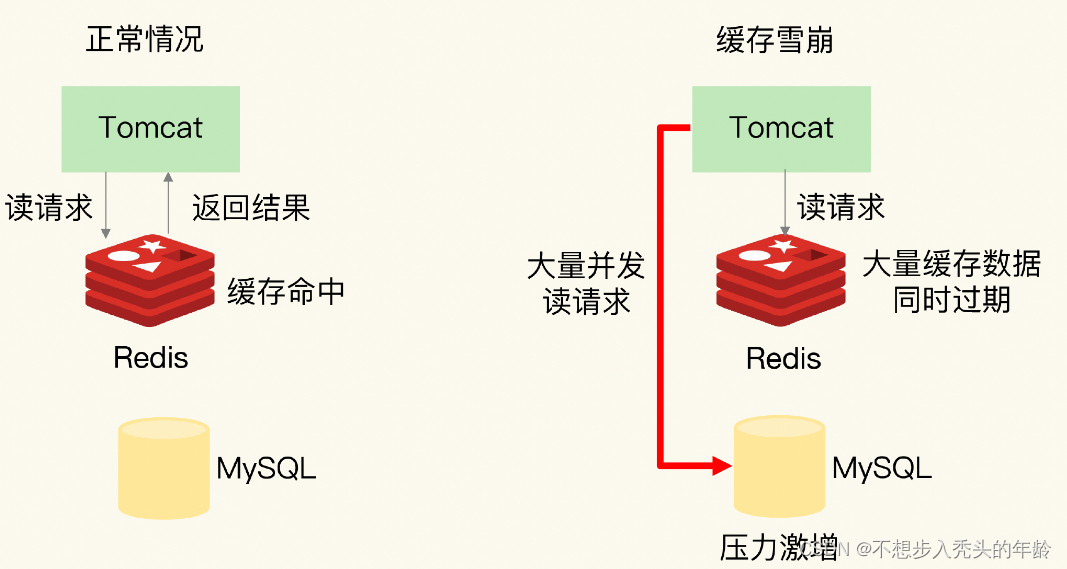
Redis中的缓存穿透、雪崩、击穿(详细)
目录 一、概念 1. 缓存穿透(Cache Penetration) 解决方案: 2. 缓存雪崩(Cache Avalanche) 解决方案: 3. 缓存击穿(Cache Breakdown) 解决方案: 二、三者出现的根本原…...

iframe
iframe学习 1.iframe是什么? a)iframe是html元素,用于在网页中内嵌另一个网页。 b)iframe默认有一个宽高,存在边界。 c)iframe是一个行内块级元素,可以通过display修改。 2.iframe元素属性有哪些? a)src : 指定内联网页的地…...

rust 基本数据类型
Rust 是 静态类型(statically typed)语言,也就是说在编译时就必须知道所有变量的类型,基本类型如下 整型 整数 是一个没有小数部分的数字长度有符号无符号8-biti8u816-biti16u1632-biti32u3264-biti64u64128-biti128u128archisi…...
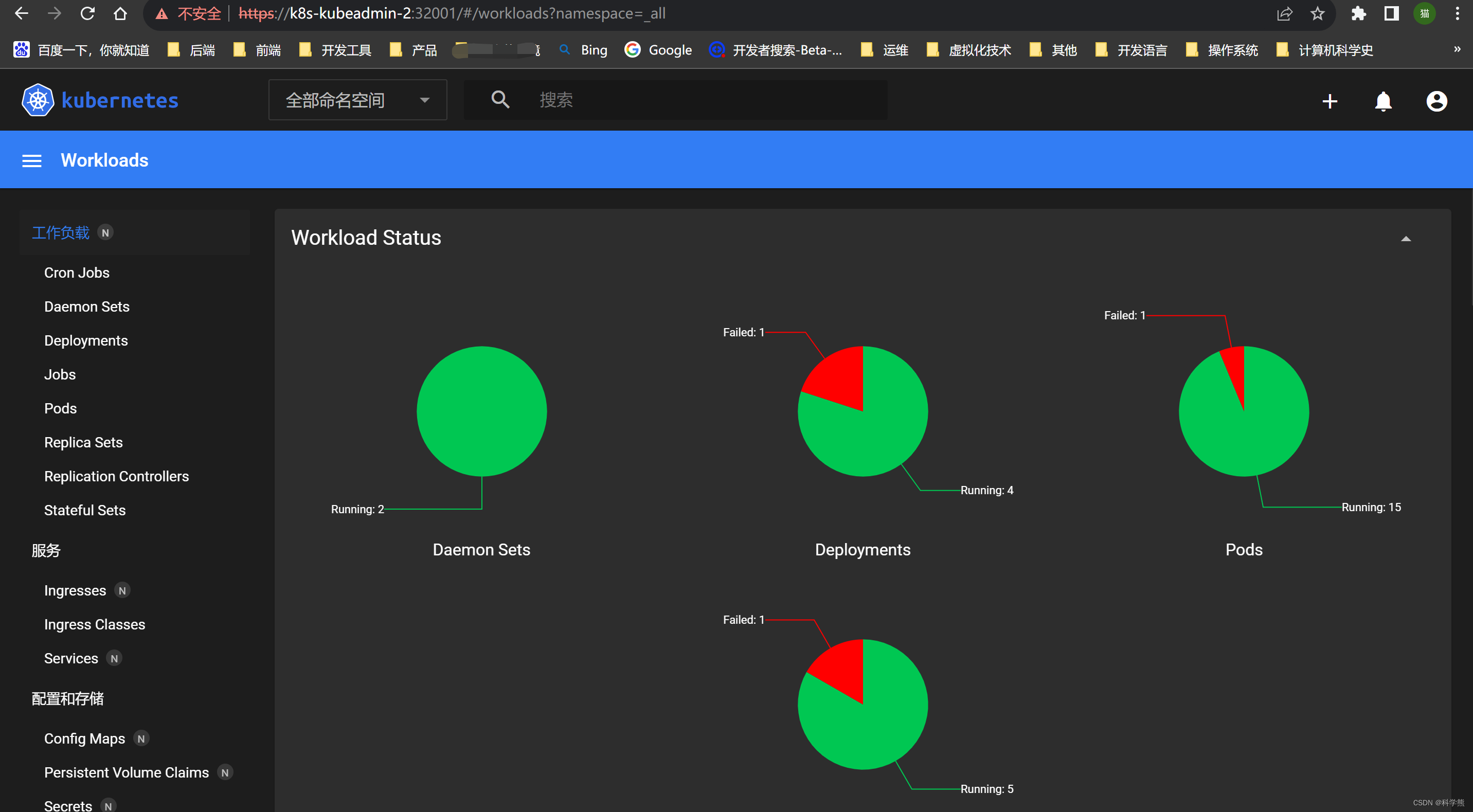
centos7中通过kubeadmin安装k8s集群
k8s部署官方提供了kind、minikube、kubeadmin等多种安装方式。 其中minikube安装在之前的文章中已经介绍过,部署比较简单。下面介绍通过kubeadmin部署k8s集群。 生产中提供了多种高可用方案: k8s官方文档 本文安装的是1.28.0版本。 建议去认真阅读一下…...

普中STM32 单片机资料
普中科技–各型号开发板资料下载链接: ①普中-精灵1开发板: 百度网盘链接:https://pan.baidu.com/s/1Pa8Ep1xmg6uoq17O6Nwyyw?pwd=1234 提取码:1234 ②普中-ESP32开发板: 百度网盘链接:https://pan.baidu.com/s/16VthcbW27oEWp162H3bi6Q?pwd=1234 提取码:1234 一…...

docker报错
安装 docker报错: Docker Desktop requires the Server service to be enabled. 解决方法: 管理员身份打开cmd,输入: services.msc开启 server 服务。 docker启动报错: 打开 docker 界面报错: Docke…...

pytest分布式执行(pytest-xdist)
前言 平常我们手工测试用例非常多时,比如有1千条用例,假设每个用例执行需要1分钟。如果一个测试人员执行需要1000分钟才能执行完,当项目非常紧急的时候,我们会用测试人力成本换取时间成本,这个时候多找个小伙伴把任务…...

spring和springBoot
Spring和Spring Boot小结 Spring和Spring Boot基于IOC AOP理念实现,Spring Boot集成了Spring。Spring框架: Spring框架解决了企业级的开发的复杂性,它是一个容器框架,用于装java对象(Bean),使程…...
laraval6.0 GatewayWorker 交互通信
laravel 6.0 GatewayWorker 通讯 开发前准备下载 GatewayWorker 及操作方式前端demo测试效果项目中安装GatewayClient 开发前准备 GatewayClient 官网:https://www.workerman.net/ 当前使用的是宝塔操作 下载 GatewayWorker 及操作方式 前端demo 测试效果 项目中安…...
循环神经网络RNN
1. 背景 RNN(Recurrent Neural Networks) CNN利用输入中的空间几何结构信息;RNN利用输入数据的序列化特性。 2. SimpleRNN单元 传统多层感知机网络假设所有的输入数据之间相互独立,但这对于序列化数据是不成立的。RNN单元用隐藏状态或记忆引入这种依赖…...

为什么预处理对象会提升处理的性能
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要环绕 “预处理对象会提升处理的性能” 这个问题做出解答以及关于预处理部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获ÿ…...

智能超声波雾化器pcba方案
一、超声波雾化器方案工作原理 超声波雾化器是一款基于电路板的振荡信号被大功率三极管进行能量放大,传递给压电陶瓷片,当压电陶瓷片受电信号的激励,产生高频谐振,并使吸附在微孔膜上的液体结产生超声振荡,将液体的结构…...

Git分支合并导致文件异常
昨天合并分支后,突然出现了项目中全部的文件出现异常。 先说结论:合并导致文件冲突处理异常,Git lfs 异常 解决方式:CMD 中执行 git lfs install git lfs pull。 合并分支后,发现项目中全部的png异常,编译a…...

Linux(11):Linux 账号管理与 ACL 权限设定
Linux 的账号与群组 每个登入的使用者至少都会取得两个 ID,一个是使用者 ID(User ID ,简称UID)、一个是群组ID (Group ID ,简称GID)。 Linux系统上面的用户如果需要登入主机以取得 shell 的环境来工作时,他需要如何进行呢? 首先…...
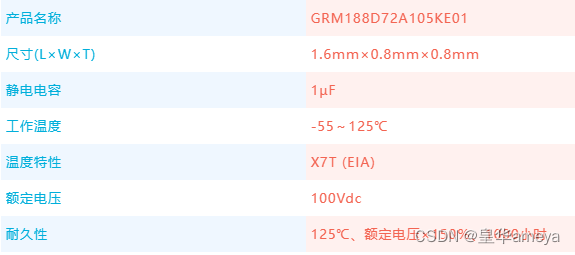
AMEYA360:村田首款1608M尺寸/100V静电容量1µF的MLCC实现商品化
株式会社村田制作所成功开发了用于基站、服务器和数据中心48V线路的多层陶瓷电容器“GRM188D72A105KE01”并已量产。该产品在1608M(1.60.8mm)尺寸、100V的额定电压下可实现1μF的超大静电容量(村田调查数据,截至2023年11月20日)。目前可向村田申请免费样品。 随着5G…...

简易键值对文本解析
除了json,xml,protobuf等成体系的配置文件外,简单的文本格式“key value”的配置文件也在很多开源项目中存在,这种配置文件的好处是简单、易于理解和编辑。 #include <stdio.h> #include <string.h>#define MAX_LINE_LENGTH 1024void Parse…...
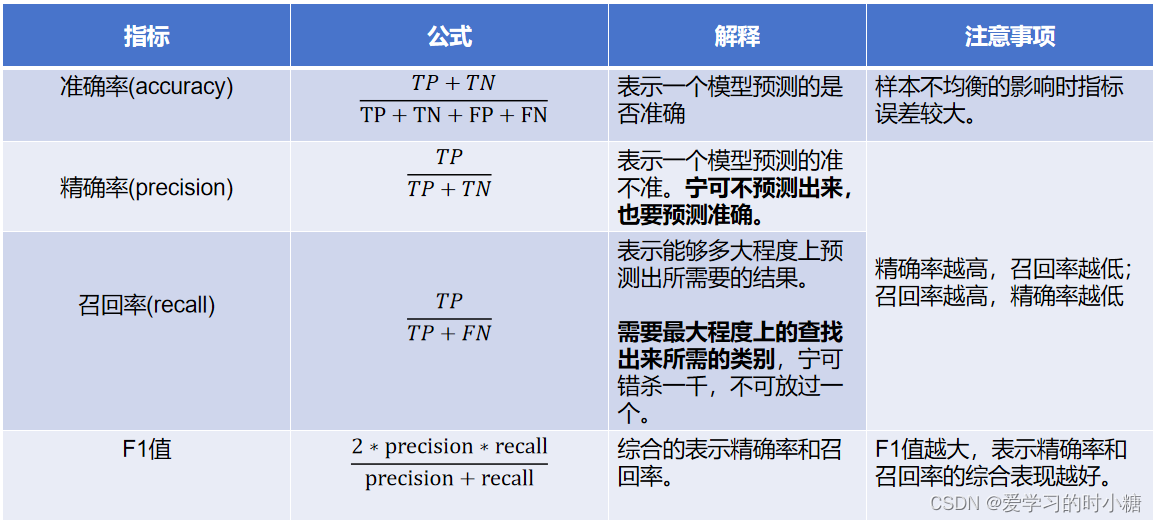
成为AI产品经理——模型评估(混淆矩阵)
一、混淆矩阵 1.混淆矩阵的介绍 混淆矩阵有两个定义positive(正例)和negative(反例)。分别代表模型结果的好和坏。 下图就是一个分类问题的混淆矩阵。横行代表真实的情况,而竖行代表预测的结果。 为了便于理解&…...

Git_git相关指令 高阶
git config pull.rebase false git config pull.rebase false是做什么的_fury_123的博客-CSDN博客 git commit 命令详解_gitcommit_辰风沐阳的博客-CSDN博客...

PC企业微信http协议逆向接口开发,发送大视频文件
产品说明 一、 hook版本:企业微信hook接口是指将企业微信的功能封装成dll,并提供简易的接口给程序调用。通过hook技术,可以在不修改企业微信客户端源代码的情况下,实现对企业微信客户端的功能进行扩展和定制化。企业微信hook接口…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
