智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.哈里斯鹰算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用哈里斯鹰算法进行无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n ) (x_n,y_n) (xn,yn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p ) p(x_p,y_p) p(xp,yp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , r } node_i=\{x_i,y_i,r\} nodei={xi,yi,r},表示以节点 ( x i , y i ) (x_i,y_i) (xi,yi)为圆心,r为监测半径的圆,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n m*n m∗n个像素点,像素点的坐标为 ( x , y ) (x,y) (x,y),目标像素点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2(3)
目标区域内像素点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为像素点 ( x , y ) (x,y) (x,y)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n (5) CoverRatio = \frac{\sum P_{cov}}{m*n}\tag{5} CoverRatio=m∗n∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.哈里斯鹰算法
哈里斯鹰算法原理请参考:https://blog.csdn.net/u011835903/article/details/108528147
该算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY
AreaX = 100;
AreaY = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径哈里斯鹰算法参数如下:
%% 设定优化参数
pop=30; % 种群数量
Max_iteration=80; %设定最大迭代次数
lb = ones(1,2*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N)];
dim = 2*N;%维度为2N,N个坐标点
5.算法结果


从结果来看,覆盖率在优化过程中不断上升,表明哈里斯鹰算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于哈里斯鹰算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.哈里斯鹰算法4.实验参数设定5.算法结果6.参考…...
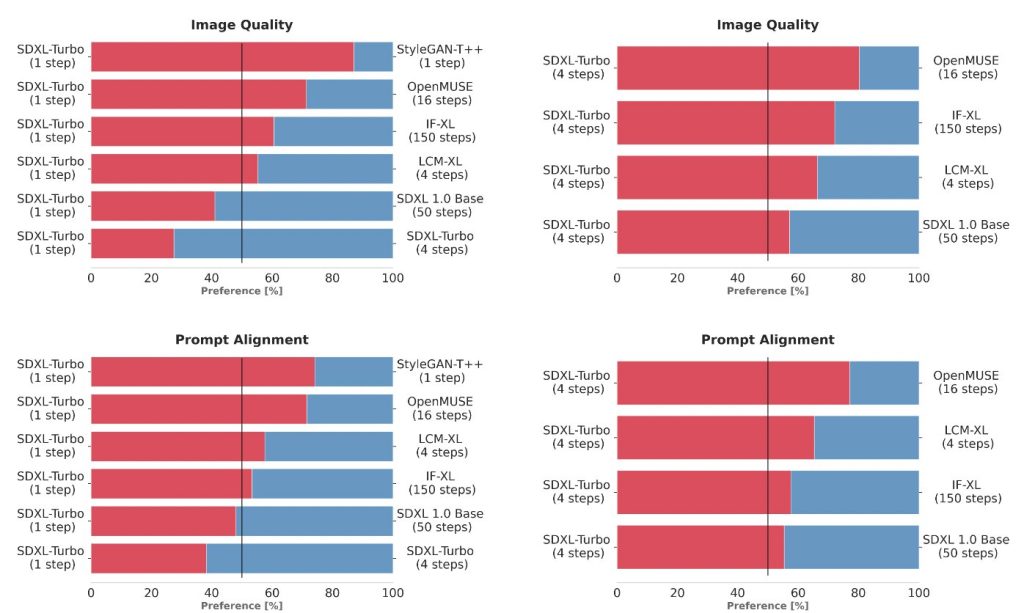
Stability AI 新发布SDXL Turbo:一款实时文本到图像生成模型
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
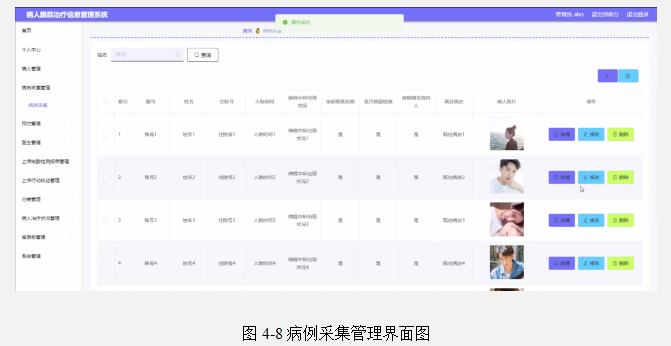
基于Java SSM框架+Vue实现病人跟踪治疗信息系统项目【项目源码+论文说明】
基于java的SSM框架Vue实现病人跟踪治疗信息系统演示 摘要 病人跟踪治疗信息管理系统采用B/S模式,促进了病人跟踪治疗信息管理系统的安全、快捷、高效的发展。传统的管理模式还处于手工处理阶段,管理效率极低,随着病人的不断增多,…...

js一行压缩库
js一行压缩库 压缩 JavaScript 代码通常是为了减小文件大小,提高加载速度。有一些常见的工具和软件可用于这个目的。以下是其中一些: UglifyJS: UglifyJS 是一个流行的 JavaScript 压缩工具,可以通过命令行或作为一个 npm 包来使…...

管理库存和出货的软件
随着时代的信息化越来越成熟,库存和出货的管理使用专门的软件变得越来越普遍。一款优秀的库存和出货管理软件应具备高效性、实时性、安全性和灵活性,以满足企业的日常运营需求。本文将详细介绍一款管理库存和出货的软件及其功能。 一、软件介绍 &#x…...

保护关键信息基础设施网络安全,SSL证书来助力
近年来,随着信息科技的飞速发展和互联网的普及应用,保护关键信息基础设施网络安全变得越来越迫切和重要。而随着《关键信息基础设施安全保护条例》的发布,保护关键信息基础设施也成为运营者必须履行的义务。SSL证书作为保护传输数据安全的重要…...
Python实现学生信息管理系统(详解版)
Python实现学生信息管理系统-详解版 个人简介实验名称:学生信息管理系统系统功能实验步骤详讲添加入住学生信息删除学生的住宿信息修改学生的住宿信息查询学生的住宿信息显示所有学生住宿信息显示所有请假学生的信息 运行截图展示1.主界面2.添加新的入住学生信息3.显…...

企业计算机服务器中了mallox勒索病毒如何解密,mallox勒索病毒文件恢复
随着网络技术的不断发展,网络安全威胁也在不断增加,勒索病毒攻击企业计算机服务器的事件时有发生,并且勒索病毒的加密形式也越来越复杂。近期,云天数据恢复中心陆续接到很多企业的求助,企业的计算机服务器遭到了mallox…...

Linux学习笔记 CenOS6.3 yum No package xxx available
环境CenOS [roothncuc ~]# cat /etc/issue CentOS release 6.2 (Final) Kernel \r on an \m安装gcc的时候提示没有包 [roothncuc ~]# sudo yum install gcc gcc-c libstdc-devel Loaded plugins: refresh-packagekit, security Setting up Install Process No package gcc a…...

【探索Linux】—— 强大的命令行工具 P.18(进程信号 —— 信号捕捉 | 信号处理 | sigaction() )
阅读导航 引言一、信号捕捉1. 内核实现信号捕捉过程2. sigaction() 函数(1)函数原型(2)参数说明(3)返回值(4)函数使用 二、可重入函数与不可重入函数1. 可重入函数条件2. 不可重入函…...
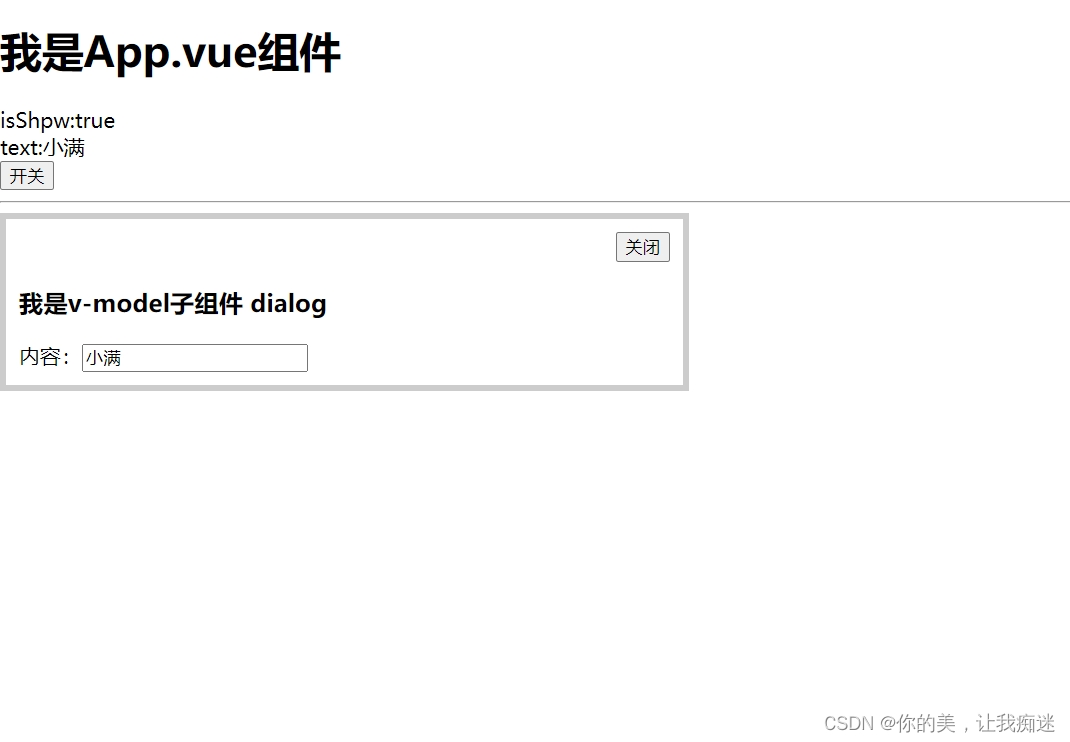
vue3+ts v-model 深度学习
<template><div><h1>我是App.vue组件</h1><div>isShpw:{{ isShow }}</div><div>text:{{ text }}</div><div><button click"isShow !isShow">开关</button></div><hr /><vModeVal…...

网络通信概述
文章目录 IP地址端口号协议三要素作用 五元组协议分层OSI七层模型TCP/IP 五层模型应用层传输层网络层数据链路层物理层 封装和分用发送方 - 封装中间转发接收方 - 分用 一般认为计算机网络就是利用通信线路和通信设备将地理上分散的、具有独立功能的多个计算机系统按不同的形式…...
<avue-crud/>,二级表头,children下字典项的dicUrl失效问题
目录 1.提出问题: 1.1 代码: 1.2 效果图:会发现处在children下的dicUrl失效了 2. 解决思路 3. 解决代码(你要的都在这,看这里) 1.提出问题: 在使用<avue-crud/>组件实现二级表头时&…...

FastApi接收不到Apifox发送的from-data字符串_解决方法
接收不到Apifox发送的from-data字符串_解决方法 问题描述解决方法弯路总结弯路描述纵观全局小结 问题描述 这里写了一个接口,功能是上传文件,接口参数是file文件和一个id字符串 gpt_router.post("/uploadfiles") async def create_upload_fi…...
)
Python高级数据结构——堆(Heap)
Python中的堆(Heap):高级数据结构解析 堆是一种基于树结构的数据结构,具有高效的插入和删除操作。在本文中,我们将深入讲解Python中的堆,包括堆的基本概念、类型、实现方式、应用场景以及使用代码示例演示…...

linux 讨论题合集(个人复习)
常规文件的权限是什么?如何分配或修改这些权限?文件夹(目录)的权限是什么?显示常规文件和文件夹的区别 讨论:①常规的文件权限有四种,r可读、w可写、x可执行、-没有权限;②可以使用c…...

浅析SD-WAN技术如何加强企业网络安全
在这个数字化时代,企业组网的安全性已经成为许多企业所面临的一个重要挑战。特别是随着云计算、移动办公等新型信息技术的普及,企业网络的规模和复杂度不断增加,网络攻击和数据泄露的威胁也日益增加。因此,企业需要采取更加有效的…...

测试相关-面试高频
测试面试相关 面试 测试的具体场景 功能测试 具体的测试工具Jmeter Postman selenium pytest 怎么看待测试的潜力与挑战 软件测试是正在快速发展,充满挑战的领域。尽管现在许多自动化测试软件的出现使得传统手工测试的方式被代替,但自动化测试工具的…...

基于Java web的多功能游戏大厅系统的开发与实现
摘 要 目前,国内游戏市场上的网络游戏有许多种类,游戏在玩法上也越来越雷同,形式越来越单调。这种游戏性系统给玩家带来的成就感虽然是无穷的,但是也有随之而来的疲惫感,尤其是需要花费大量的时间和精力,这…...

【MySQL工具】my2sql-快速解析binlog
目录 安装 my2sql简介 用途 工具优势 限制 账号所需权限 参数解析 场景 场景1 回滚 场景2 生成正向SQL 场景3 DML与事务统计 场景4 解析本地 与binlog2sql性能对比 安装 安装比较简单 直接下载二进制命令即可使用 wget https://git…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
