C++ CryptoPP使用RSA加解密
Crypto++ (CryptoPP) 是一个用于密码学和加密的 C++ 库。它是一个开源项目,提供了大量的密码学算法和功能,包括对称加密、非对称加密、哈希函数、消息认证码 (MAC)、数字签名等。Crypto++ 的目标是提供高性能和可靠的密码学工具,以满足软件开发中对安全性的需求。RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,由三位密码学家Ron Rivest、Adi Shamir和Leonard Adleman于1977年共同提出。RSA算法被广泛应用于信息安全领域,特别是在数字签名和密钥交换等场景中。
以下是RSA加密算法的主要概述:
- 非对称加密: RSA是一种非对称加密算法,使用一对公钥和私钥。公钥用于加密,私钥用于解密。这种非对称性质使得RSA在密钥交换和数字签名方面有着重要的应用。
- 大数分解: RSA的安全性基于大数分解问题的困难性。具体而言,RSA的安全性取决于将两个大质数相乘得到的结果难以分解为这两个质数的乘积。当前的技术水平下,对大数的分解仍然是一项困难的任务,从而确保了RSA的安全性。
- 密钥生成: RSA密钥生成包括选择两个大素数、计算其乘积(模数)和选择与欧拉函数互质的指数。这些步骤最终生成了公钥和私钥。
- 加密过程: 加密者使用接收者的公钥对消息进行加密。RSA的加密过程涉及模数的幂运算,其计算复杂度较高。
- 解密过程: 只有持有私钥的接收者才能解密消息。解密过程涉及模数的私钥指数的幂运算,从而得到原始消息。
- 数字签名: RSA可以用于数字签名,用私钥对消息的哈希值进行签名,而任何人都可以使用相应的公钥验证签名的有效性。这在确保消息完整性和身份验证方面非常有用。
- 密钥交换: RSA也广泛用于密钥交换,例如在安全套接字层(SSL/TLS)协议中。两方可以使用对方的公钥加密会话密钥,而只有持有相应私钥的一方才能解密会话密钥。
- 安全性: RSA的安全性依赖于大数分解问题的难解性。随着计算能力的增强,密钥长度需要不断增加以保持安全性。一般而言,2048比特或3072比特的密钥长度被认为是安全的。
总体而言,RSA是一种强大而灵活的加密算法,广泛用于保护通信的机密性、完整性和身份验证。由于其非对称性质,RSA在密钥交换和数字签名等场景中发挥着重要作用。
关键特点
- 非对称加密: RSA是一种非对称加密算法,使用两个密钥:公钥和私钥。公钥用于加密,私钥用于解密。
- 数学基础: RSA的安全性基于数论的难题,主要是大数因子分解。其原理是利用大质数的乘积很容易计算,但给定乘积却难以分解出其质因数。
- 密钥生成: RSA的密钥生成包括选择两个大质数,计算它们的乘积作为模数,并选择一个与欧拉函数互质的公钥指数。私钥则是根据公钥指数和模数计算得到的。
- 加解密过程:
- 加密:使用接收者的公钥对消息进行加密。
- 解密:只有接收者拥有相应的私钥才能解密消息。
- 数字签名: 除了加密和解密,RSA还可用于数字签名。发送者使用私钥对消息进行签名,接收者使用发送者的公钥来验证签名的真实性和完整性。
- 密钥长度: RSA密钥的长度通常以比特位为单位表示,常见的长度包括1024位、2048位和3072位。较长的密钥长度提供更高的安全性,但也可能导致性能损失。
- 应用领域: RSA广泛应用于数据加密、数字签名、密钥交换等场景。它是许多安全通信协议(如TLS、SSH)和数字证书的基础。
加解密流程
- 密钥生成: 选择两个大质数(p和q),计算它们的乘积N。选择公钥指数e,满足e与(N)的欧拉函数ϕ(N)互质。计算私钥指数d,使得(e * d) mod ϕ(N) = 1。
- 加密与解密过程:

RSA算法的安全性基于大整数因子分解的困难性,因此密钥的长度选择至关重要。随着计算能力的提高,一般建议使用2048位或更长的密钥以确保足够的安全性。
函数API概述
AutoSeededRandomPool 类
用于提供安全的伪随机数生成器。这个类会根据系统的熵源自动初始化,以确保生成的随机数足够安全。在 Crypto++ 库中,伪随机数生成器是通过 RandomNumberGenerator 接口实现的。AutoSeededRandomPool 是 RandomNumberGenerator 接口的一个具体实现。
InvertibleRSAFunction 类。
在 RSA 加密系统中,InvertibleRSAFunction 通常用于存储 RSA 密钥的信息,包括公钥和私钥。这个类通常与 RSA::PublicKey 和 RSA::PrivateKey 一起使用。InvertibleRSAFunction 存储了 RSA 密钥的模数(modulus)和指数(exponent),而 RSA::PublicKey 和 RSA::PrivateKey 则分别包含了公钥和私钥的其他相关信息。
RSA::PrivateKey 类
是 Crypto++ 中用于表示 RSA 私钥的类。RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,它使用一对密钥:公钥和私钥。私钥用于解密或签名,而公钥用于加密或验证签名。
在 Crypto++ 中,RSA::PrivateKey 包含了 RSA 密钥的关键信息,包括模数(Modulus)和私钥指数(Private Exponent)。这些信息是在生成 RSA 密钥对时使用 InvertibleRSAFunction 类生成的。
以下是 RSA::PrivateKey 类的一些关键成员和作用:
- 构造函数:
PrivateKey类的构造函数接受一个InvertibleRSAFunction对象作为参数,用于初始化私钥的关键信息。 - GetModulus() 方法:获取私钥的模数。模数是 RSA 算法中的一个关键参数,用于加密和解密操作。
- GetPrivateExponent() 方法:获取私钥的指数。私钥指数是 RSA 算法中的另一个关键参数,用于解密和签名操作。
私钥是安全性关键的信息,应当妥善保护。在使用 RSA 进行加密、解密、签名或验证时,相应的密钥对(公钥和私钥)必须配套使用。私钥不应该暴露给不信任的方,而公钥则可以公开分享。
RSA::PublicKey 类
是 Crypto++ 中用于表示 RSA 公钥的类。RSA(Rivest-Shamir-Adleman)是一种非对称加密算法,它使用一对密钥:公钥和私钥。公钥用于加密或验证签名,而私钥用于解密或签名。
RSA::PublicKey 包含了 RSA 密钥的关键信息,包括模数(Modulus)和公钥指数(Public Exponent)。这些信息是在生成 RSA 密钥对时使用 InvertibleRSAFunction 类生成的。
以下是 RSA::PublicKey 类的一些关键成员和作用:
- 构造函数:
PublicKey类的构造函数接受一个InvertibleRSAFunction对象作为参数,用于初始化公钥的关键信息。 - GetModulus() 方法:获取公钥的模数。模数是 RSA 算法中的一个关键参数,用于加密和解密操作。
- GetPublicExponent() 方法:获取公钥的指数。公钥指数是 RSA 算法中的另一个关键参数,用于加密和验证签名操作。
公钥是用于加密和验证签名的关键信息,通常可以被分享给其他人或实体。然而,私钥仍然应该被妥善保护,因为私钥用于解密和签名,是安全性关键的信息。
**RSAES_OAEP_SHA_Encryptor **
是 Crypto++ 中用于实现 RSA-OAEP(Optimal Asymmetric Encryption Padding)加密的类。RSA-OAEP 是一种非对称加密方案,广泛用于保护信息的机密性。
以下是 RSAES_OAEP_SHA_Encryptor 类的一些关键概述:
- 功能:
RSAES_OAEP_SHA_Encryptor类实现了基于 RSA-OAEP 方案的加密功能。它通过 RSA 公钥对输入数据进行加密,使用 OAEP 进行填充。 - 构造函数:该类的构造函数接受一个 RSA 公钥作为参数,用于初始化加密器。公钥包含了加密操作所需的关键信息,如模数和指数。
- 加密操作:通过调用
ProcessBlock方法执行加密操作。这个方法接受待加密的数据块和一个随机数生成器作为参数,并返回加密后的数据块。 - 数据填充:RSA-OAEP 使用 Optimal Asymmetric Encryption Padding 进行数据填充。这是一种具有良好安全性属性的填充方案,旨在提供对抗各种攻击,包括选择密文攻击。
- 安全性:RSA-OAEP 是一种安全的加密方案,提供了对抗许多已知攻击的强大保护。然而,它的安全性仍然依赖于正确的实现和使用。
**RSAES_OAEP_SHA_Decryptor **
是 Crypto++ 中用于实现 RSA-OAEP(Optimal Asymmetric Encryption Padding)解密的类。RSA-OAEP 是一种非对称加密方案,广泛用于保护信息的机密性。
以下是 RSAES_OAEP_SHA_Decryptor 类的一些关键概述:
- 功能:
RSAES_OAEP_SHA_Decryptor类实现了基于 RSA-OAEP 方案的解密功能。它通过 RSA 私钥对输入数据进行解密,使用 OAEP 进行填充。 - 构造函数:该类的构造函数接受一个 RSA 私钥作为参数,用于初始化解密器。私钥包含了解密操作所需的关键信息,如模数和指数。
- 解密操作:通过调用
ProcessBlock方法执行解密操作。这个方法接受待解密的数据块和一个随机数生成器作为参数,并返回解密后的数据块。 - 数据填充:RSA-OAEP 使用 Optimal Asymmetric Encryption Padding 进行数据填充。这是一种具有良好安全性属性的填充方案,旨在提供对抗各种攻击,包括选择密文攻击。
- 安全性:RSA-OAEP 是一种安全的解密方案,提供了对抗许多已知攻击的强大保护。然而,它的安全性仍然依赖于正确的实现和使用。
#include <Windows.h>
#include <iostream>#include <rsa.h>
#include <files.h>
#include <osrng.h>
#include <base64.h>
#include <hex.h>
#include <randpool.h>using namespace std;
using namespace CryptoPP;#pragma comment(lib,"cryptlib.lib")// 生成RSA密钥对
void GenerateRSAKeyPair(RSA::PrivateKey& privateKey, RSA::PublicKey& publicKey)
{AutoSeededRandomPool rng;InvertibleRSAFunction parameters;parameters.GenerateRandomWithKeySize(rng, 2048);privateKey = RSA::PrivateKey(parameters);publicKey = RSA::PublicKey(parameters);
}// RSA加密
std::string RSAEncrypt(const RSA::PublicKey& publicKey, const std::string& plainText)
{AutoSeededRandomPool rng;RSAES_OAEP_SHA_Encryptor encryptor(publicKey);std::string cipherText;StringSource(plainText, true,new PK_EncryptorFilter(rng, encryptor,new StringSink(cipherText)));return cipherText;
}// RSA解密
std::string RSADecrypt(const RSA::PrivateKey& privateKey, const std::string& cipherText)
{AutoSeededRandomPool rng;RSAES_OAEP_SHA_Decryptor decryptor(privateKey);std::string recoveredText;StringSource(cipherText, true,new PK_DecryptorFilter(rng, decryptor,new StringSink(recoveredText)));return recoveredText;
}
上述代码中GenerateRSAKeyPair用与临时生成密钥对,RSAEncrypt用于对数据加密,RSADecrypt则用于对数据解密操作,如下所示;
int main(int argc, char* argv[])
{try{RSA::PrivateKey privateKey;RSA::PublicKey publicKey;// 生成RSA密钥对GenerateRSAKeyPair(privateKey, publicKey);// 待加密的文本std::string plainText = "Hello, LyShark !";// RSA加密std::string cipherText = RSAEncrypt(publicKey, plainText);std::cout << "Cipher Text: " << cipherText << std::endl;// RSA解密std::string recoveredText = RSADecrypt(privateKey, cipherText);std::cout << "Recovered Text: " << recoveredText << std::endl;}catch (CryptoPP::Exception& e){std::cerr << "Crypto++ Exception: " << e.what() << std::endl;return 1;}system("pause");return 0;
}
运行效果图如下图所示;

相关文章:

C++ CryptoPP使用RSA加解密
Crypto (CryptoPP) 是一个用于密码学和加密的 C 库。它是一个开源项目,提供了大量的密码学算法和功能,包括对称加密、非对称加密、哈希函数、消息认证码 (MAC)、数字签名等。Crypto 的目标是提供高性能和可靠的密码学工具,以满足软件开发中对…...
从实践角度深入探究数据驱动和关键字驱动测试方法!
数据驱动 数据驱动,指在软件测试领域当中的数据驱动测试(Data-Driven Testing,简称DDT)是⼀种软件测试⽅法,在不同的数据下重复执⾏相同顺序的测试步骤,测试脚本从数据源读取测试数据,⽽不使⽤…...

Unity收费对谁影响最大
Unity的收费政策对以下几类人群影响最大: 游戏开发商:Unity收费政策中最直接的影响对象就是游戏开发商。对于那些使用Unity引擎制作游戏的开发商来说,他们将需要考虑新的许可证费用和服务费用,这可能会对他们的盈利和发展产生影响…...
信号收尾.
sigaction 信号捕捉 它也是信号捕捉,不仅能处理普通信号还能处理实时信号,但我们不管实时信号 我们发现函数名和形参中结构体名一样都是sigaction,这在c/c中允许吗? 不建议,但是可以 signo你要捕捉几号信号 输入型参…...

maven 常用命令解析
目录 maven 是什么 Maven 目录结构 maven 常用命令解析 mvn clean mvn validate mvn compile mvn test mvn package mvn verify mvn install mvn site mvn deploy maven 是什么 Maven 是一个流行的项目管理和构建工具,用于帮助开发人员管理 Java 项目的…...

ESP32-Web-Server编程-JS 基础 1
ESP32-Web-Server编程-JS 基础 1 概述 前述分别在 HTML 基础 和 CSS 基础 中介绍了 HTML、CSS 的基本内容。HTML 定义了网页中包含哪些对象,CSS 定义了对象的显示样式。JavaScript(LiveScript)是一种运行于客户端的解释性脚本语言,使 HTML 页面更具动态…...

代码随想录算法训练营第23天|● 669. 修剪二叉搜索树 ● 108.将有序数组转换为二叉搜索树 ● 538.把二叉搜索树转换为累加树 ● 总结篇
108. 将有序数组转换为二叉搜索树 简单 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 示例 1: …...

UniApp 中的 u-input 属性讲解
在 UniApp 中,u-input 是一个常用的组件,用于接收用户的输入。它具有多种属性,用于控制输入框的样式和行为。下面我将为您讲解一些常用的 u-input 属性。 基本属性 value:表示输入框的初始值,可以使用 v-model 进行双…...
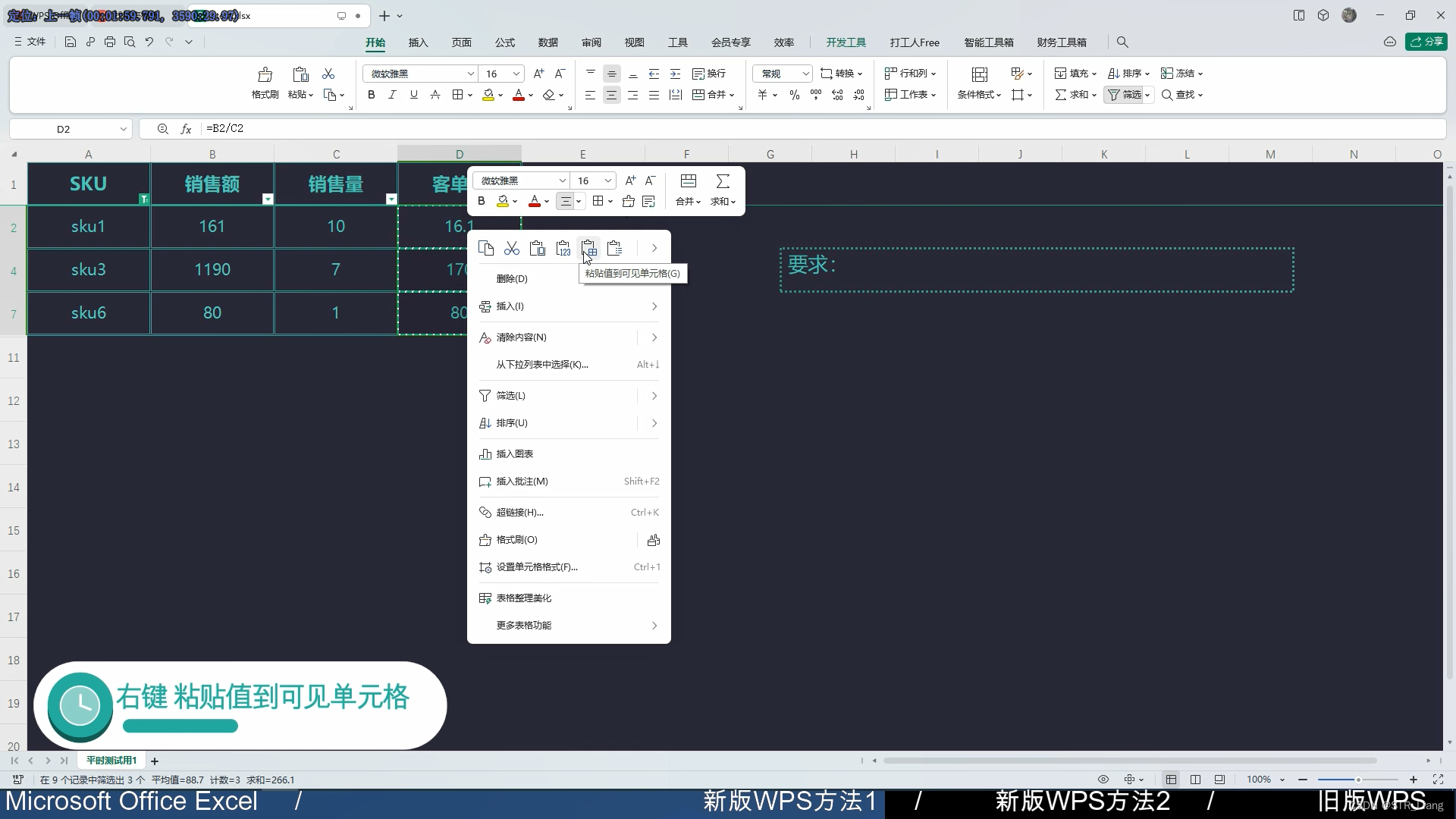
解决方案:新版WPS-右键粘贴值到可见单元格没有了
WPS筛序后复制,并且粘贴到可见单元格 (如果直接粘贴数据会乱掉) 旧版WPS,右键就能出现 但是新版WPS不是在这里(方法1) 新版WPS(方法2) 视频详细教程链接:解决方案&…...

pat模拟题—7-11 两个序列的中位数
一个长度为n(n⩾1)的升序序列S,处在第2n个位置的数称为序列S的中位数(median number),例如,序列S1{10,13,14,16,18,19}的中位数是14。两个序列的中位数是它们所有元素的升序序列的中位数,例如,S2{2,4,8,9,20,21},则S1和S2的中位数是13。现有…...

Java中的i++是原子操作吗?
我们都知道i分为三步进行,分别是1:取到当前i的值,2:,3:将最终结果赋值 因此我们可通过创建两个线程,对同一个变量count,一个线程对count进行递增操作,另一个线程对count进行递减操作。每个线程…...

git commit message 书写规范
在使用 Git 提交时,遵循良好的提交消息规范可以提高代码的可读性和可维护性。以下是一些常见的 Git 提交消息书写规范: 提交消息格式:一个提交消息通常包含三个部分:标题、空行和正文。它们之间使用空行分隔。 复制 <标题>&…...

sql 注入 ctf wiki
部分转载ctf-wiki 判闭合形式: 哪个报错就是哪种 1,1’,1’‘,1’,1’(双引号带括号) 万能密码: admin’ – admin’ # admin’/* ’ or 11– ’ or 11# ’ or 11/* ) or ‘1’1– ) or (‘1’1– 数据库名: SEL…...

Flutter创建TabBar
使用TabBar和TabBarView来创建一个包含"首页"、"分类"和"我的"的TabBar。每个Tab对应一个Tab控件,TabBarView中的每个页面对应一个Widget。 1.Tab使用自定义图标和颜色 一般UI设计的图会带渐变色之类的,应该保持图片的原…...

双流网络论文精读笔记
精读视频:双流网络论文逐段精读【论文精读】_哔哩哔哩_bilibili Two-Stream Convolutional Networks for Action Recognition in Videos 传统的神经网络难以学习到物体的运动信息,双流网络则通过光流将物体运动信息抽取出来再传递给神经网络 给模型提供…...

机器人与3D视觉 Robotics Toolbox Python 一 安装 Robotics Toolbox Python
一 安装python 库 前置条件需要 Python > 3.6,使用pip 安装 pip install roboticstoolbox-python测试安装是否成功 import roboticstoolbox as rtb print(rtb.__version__)输出结果 二 Robotics Toolbox Python样例程序 加载机器人模型 加载由URDF文件定义…...

JS之Object.defineProperty方法
给对象添加属性的方法有许多,这次让我为大家介绍一种给对象添加属性的静态方法吧! 语法:Objcet.defineProperty(对象的名称,“添加的键名”,{value:键值}) const obj {name:"张三",age:18}// 我…...
卷积神经网络(CNN)注意力检测
文章目录 一、前言二、前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)2. 导入数据3. 查看数据 二、数据预处理1.加载数据2. 可视化数据4. 配置数据集 三、调用官方网络模型四、设置动态学习率五、编译六、训练模型七、模型评估1. Accuracy与Loss图2. …...

4. 权限,特权
对数据段特权检查对直接转移的代码段特权检查栈段的检查调用门的检查 权限问题: 由于CPL,DPL 无法完整表达权限的问题. 例如用户程序(CPL3)通过调用门(将调用到内核过程,从低权限到高权限)执行,此时CPL0,此时可以为所欲为.因此加入RPL.此参数由操作系统来保证,CPU仅使用 RPL:…...

云原生系列Go语言篇-泛型Part 2
类型推导和泛型 就像在使用:时支持类型推导一样,在调用泛型函数时Go同样支持类型推导。可在上面对Map、Filter和Reduce调用中看出。有些场景无法进行类型推导(如类型参数仅用作返回值)。这时,必…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
