C/C++ 常用的四种查找算法
在计算机科学中,搜索算法是一种用于在数据集合中查找特定元素的算法。C语言作为一种强大的编程语言,提供了多种搜索算法的实现方式。本文将介绍C语言中的四种常见搜索算法其中包括(线性查找,二分法查找,树结构查找,分块查找),并提供每种算法的简单实现示例。
常见的查找算法主要有以下几种:
- 线性查找(Linear Search):
- 简单直观,适用于无序列表。
- 从列表的一端开始逐个元素比较,直到找到目标元素或遍历完整个列表。
- 二分查找(Binary Search):
- 适用于有序列表。
- 每次将目标值与中间元素比较,可以迅速缩小搜索范围。
- 树结构查找(树的各种形式,如二叉搜索树、AVL树、红黑树等):
- 通过树结构,可以更加高效地进行查找、插入和删除操作。
- 二叉搜索树要求左子树上所有结点的值小于根结点的值,右子树上所有结点的值大于根结点的值。
- 分块查找(Block Search):
- 将数据分成若干块,每一块中的元素无序,但块与块之间有序。
- 先确定目标元素所在的块,再在块内进行线性查找。
这些查找算法各自有适用的场景和优势,选择合适的查找算法取决于数据的特性以及实际应用的需求。
线性查找(Linear Search)
线性搜索,又称为顺序搜索(Sequential Search),是一种简单直观的查找算法。该算法通过顺序遍历数据集,逐一比较每个元素与目标值是否相等,直到找到目标值或遍历完整个数据集。
算法步骤
- 从头到尾遍历数据集: 从数据集的第一个元素开始,依次比较每个元素与目标值是否相等。
- 比较目标值: 对于每个元素,与目标值进行比较。
- 找到目标值: 如果找到了与目标值相等的元素,返回该元素的位置或索引。
- 遍历完整个数据集: 如果遍历完整个数据集仍未找到目标值,返回未找到的标记(通常是一个特殊值,如-1)。
特点
- 适用于小型数据集: 线性搜索适用于小型数据集,对于大型数据集可能效率较低。
- 无序数据: 不依赖数据的排列顺序,适用于无序数据。
- 简单直观: 实现简单,易于理解。
线性搜索是最简单的搜索算法之一,它按顺序遍历数据集合,查找目标元素。以下是一个线性搜索的C语言示例:
#include <stdio.h>int linearSearch(int arr[], int n, int target)
{for (int i = 0; i < n; i++){if (arr[i] == target){return i; // 找到则返回索引}}return -1; // 未找到则返回-1
}int main(int argc, char *argv[])
{int arr[] = {1, 2, 3, 4, 5};int n = sizeof(arr) / sizeof(arr[0]);int target = 3;int result = linearSearch(arr, n, target);if (result != -1){printf("元素在索引 %d 处找到\n", result);} else{printf("未找到元素\n");}return 0;
}
二分查找(Binary Search)
二分搜索(Binary Search)是一种在有序数组中查找目标值的算法。它通过反复将查找范围划分为两半并比较目标值与中间元素的大小,从而缩小搜索范围,直到找到目标值或确定目标值不存在。
算法步骤
- 初始化: 确定搜索范围的起始点
left和终止点right。 - 循环条件: 当
left小于等于right时执行循环。 - 计算中间位置: 计算中间位置
mid,mid = (left + right) / 2。 - 比较目标值: 将目标值与中间元素进行比较。
- 如果目标值等于中间元素,找到目标,返回索引。
- 如果目标值小于中间元素,说明目标值在左半部分,更新
right = mid - 1。 - 如果目标值大于中间元素,说明目标值在右半部分,更新
left = mid + 1。
- 循环结束: 当
left大于right,表示搜索范围为空,未找到目标值。
特点
- 有序数组: 二分搜索要求数组是有序的,以便通过比较中间元素确定目标值在哪一半。
- 高效性: 由于每一步都将搜索范围缩小一半,因此二分搜索的平均时间复杂度为 O(log n)。
- 适用性: 适用于静态数据集或很少变化的数据集,不适用于频繁插入、删除操作的动态数据集。
二分搜索要求数据集合是有序的,以下是一个二分搜索的C语言示例:
#include <stdio.h>int binary_search(int key, int a[], int n)
{int low, high, mid, count = 0, count1 = 0;low = 0;high = n - 1;while (low<high){count++; // 记录查找次数mid = (low + high) / 2; // 求出中间位置if (key<a[mid]) // 当key小于中间值high = mid - 1; // 确定左子表范围else if (key>a[mid]) // 当key大于中间值low = mid + 1; // 确定右子表范围else if (key == a[mid]) // 当key等于中间值证明查找成功{printf("查找元素: %d Array[%d]=%d\n", count, mid, key);count1++; //count1记录查找成功次数break;}}if (count1 == 0)return 0;
}int main(int argc, char *argv[])
{int number = 10, key = 6;int Array[10] = { 1, 5, 6, 7, 9, 3, 4, 6, 0, 2 };binary_search(key, Array, number);return 0;
}
二叉搜索树 (BST)
二叉搜索树(Binary Search Tree,BST)是一种二叉树数据结构,其中每个节点都有一个键值,且满足以下性质:
- 对于树中的每个节点,其左子树中的所有节点的键值都小于该节点的键值。
- 对于树中的每个节点,其右子树中的所有节点的键值都大于该节点的键值。
- 左、右子树也分别为二叉搜索树。
这个性质使得在二叉搜索树中可以高效地进行搜索、插入和删除操作。
特点
- 有序性: 由于BST的定义,其中的元素是有序排列的。对于任意节点,其左子树的值小于该节点,右子树的值大于该节点,因此通过中序遍历BST可以得到有序的元素序列。
- 高效的搜索操作: 由于有序性,可以通过比较键值快速定位目标节点,使搜索操作的平均时间复杂度为 O(log n)。在最坏情况下(树退化为链表),搜索的时间复杂度为 O(n)。
- 高效的插入和删除操作: 插入和删除操作也涉及到比较键值和调整树的结构,平均情况下的时间复杂度为 O(log n)。在最坏情况下,树可能变得不平衡,导致时间复杂度为 O(n),但通过平衡二叉搜索树(如 AVL 树、红黑树等)可以保持树的平衡。
操作
- 搜索(Search): 从根节点开始比较目标值,根据比较结果选择左子树或右子树,直到找到目标节点或达到叶子节点。
- 插入(Insert): 从根节点开始,按照比较结果选择左子树或右子树,直到找到合适的插入位置,插入新节点。
- 删除(Delete): 找到要删除的节点,可能有以下几种情况:
- 若该节点为叶子节点,直接删除。
- 若该节点有一个子节点,用子节点替代该节点。
- 若该节点有两个子节点,找到右子树中的最小节点或左子树中的最大节点,替代该节点,并递归删除被替代的节点。
以下是一个简化的BST的C语言示例:
#include <stdio.h>
#include <stdlib.h>struct Node
{int key;struct Node *left, *right;
};struct Node* newNode(int key)
{struct Node* node = (struct Node*)malloc(sizeof(struct Node));node->key = key;node->left = node->right = NULL;return node;
}struct Node* insert(struct Node* root, int key)
{if (root == NULL)return newNode(key);if (key < root->key)root->left = insert(root->left, key);else if (key > root->key)root->right = insert(root->right, key);return root;
}int main(int argc, char *argv[])
{struct Node* root = NULL;int keys[] = {3, 1, 5, 2, 4};for (int i = 0; i < sizeof(keys) / sizeof(keys[0]); i++){root = insert(root, keys[i]);}// 可以在 'root' 上执行BST操作return 0;
}
分块查找(Block Search)
分块搜索(Block Search)是一种在查找大量数据中的目标值时,将数据分成若干块,然后在块内进行查找的策略。这种方法适用于一些动态更新频繁,但每次更新数据量较小的场景。
算法步骤
- 数据分块: 将大量数据按照一定的规则分成若干块。
- 建立索引表: 对每个块建立索引,记录每块的起始位置、结束位置和关键字(通常是块内最大的关键字)。
- 查找块: 根据目标值的大小确定它可能在哪个块中,找到相应的块。
- 在块内查找: 在确定的块内使用线性查找或其他查找算法寻找目标值。
特点
- 适用于动态数据: 分块搜索适用于数据集动态更新的情况,因为每次更新数据只需更新相应块的索引。
- 索引表: 建立索引表有助于快速定位目标值可能存在的块,提高查找效率。
- 非均匀分块: 可以根据数据的特点进行非均匀分块,以适应不同数据分布情况。
该查找与二分查找类似,都是对半分,分块则可以分为多块,效率更高一些。如下这段C语言代码实现了分块查找算法。分块查找是一种基于块的数据结构的搜索算法,通过将数据集划分为若干块(或称为块),并为每个块建立一个索引。每个索引记录了该块的起始位置、结束位置以及该块内元素的最大值。
#include <stdio.h>struct index //定义块的结构
{int key;int start;int end;
}index_table[4]; //定义结构体数组int block_search(int key, int a[]) //自定义实现分块查找
{int i, j;i = 1;while (i <= 3 && key>index_table[i].key) //确定在哪个块中i++;if (i>3) //大于分得的块数,则返回0return 0;j = index_table[i].start; //j等于块范围的起始值while (j <= index_table[i].end&&a[j] != key) //在确定的块内进行查找j++;if (j>index_table[i].end) //如果大于块范围的结束值,则说明没有要查找的数j = 0;return j;
}int main(int argc, char *argv[])
{int x, y = 0,ref = 0;int key = 8;int Array[16] = { 1, 3, 4, 5, 6, 7, 8, 9, 0, 4, 3, 5, 6, 7, 8, 9 };for (x = 1; x <= 3; x++){index_table[x].start = y + 1; // 确定每个范围的起始行y = y + 1;index_table[x].end = y + 4; // 确定每个块范围的结束值y = y + 4;index_table[x].key = Array[y]; // 确定每个块范围中元素的最大值}ref = block_search(key, Array);if (ref != 0){printf("position is: %d \n", ref);}return 0;
}
相关文章:

C/C++ 常用的四种查找算法
在计算机科学中,搜索算法是一种用于在数据集合中查找特定元素的算法。C语言作为一种强大的编程语言,提供了多种搜索算法的实现方式。本文将介绍C语言中的四种常见搜索算法其中包括(线性查找,二分法查找,树结构查找&…...
Linux | Ubuntu设置 netstat(网络状态)
netstat命令用于显示与IP、TCP、UDP和ICMP协议相关的统计数据,一般用于检验本机各端口的网络连接情况。netstat是在内核中访问网络及相关信息的程序,它能提供TCP连接,TCP和UDP监听,进程内存管理的相关报告。 1.netstat的安装 搜…...
成为AI产品经理——模型构建流程(下)
目录 1.模型训练 2.模型验证 3.模型融合 4.模型部署 上节课我们讲了模型设计、特征工程,这节课我们来讲模型构建剩下的三个部分:模型训练、模型验证和模型融合。 1.模型训练 模型训练就是要不断地训练、验证、调优直至让模型达到最优。 那么怎么达…...

TCP Socket API 讲解,以及回显服务器客户端的实现
文章目录 TCPServerSocket APISocket API TCP 客户端服务器的实现 TCP ServerSocket API ServerSocket 是创建TCP服务端 Socket 的 API。 serverSocket构造方法: 方法签名方法说明ServerSocket(int port)创建一个服务端流套接字Socket,并绑定到指定端…...
2023年掌控安全学院CTF暖冬杯——数据流分析
前言:打工仔一枚,第一波上新的3题misc 做完了 再打ISCTF随便记录一下 PS:环境关了,题目描述忘记了,反正就是找flag。 筛选HTTP数据流 导出数据流慢慢看 ctrl F 搜flag 看到一条 有flag.txt 的数据 导出另存.zip 这里…...
UE4 基础篇十四:自定义插件
文末有视频地址和git地址 一、概念 虚幻里插件都是用C++写的,C++包括.h文件和.cpp文件,.h头文件通常包含函数类型和函数声明,cpp文件包含这些类型和函数的实现, 你为项目编写的所有代码文件都必须位于模块中,模块就是硬盘里的一个文件夹,包含名为“Build.cs”的C#文件…...
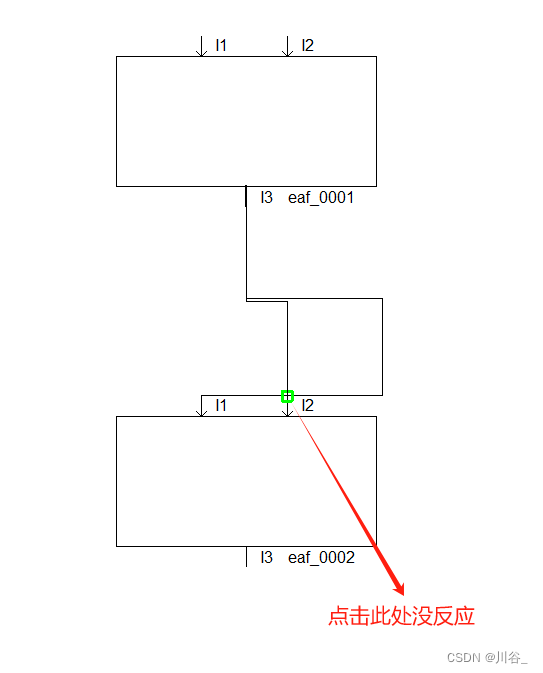
QT QGraphicsItem 图元覆盖导致鼠标点击事件不能传递到被覆盖图元
一、概述 在日常开发中,遇到这样一个问题,线图元和引脚图元重叠,导致点击引脚图元,没有进入引脚图元的鼠标点击事件中。 二、产生原因 如果您的 QGraphicsItem 上有一个图元覆盖了它,可能会导致鼠标事件无法正常触发…...

proto语法学习笔记
proto语法学习笔记 Protocol Buffers(Proto是由谷歌开发的一种数据序列化格式。 Proto 不是一种编程语言,而是一种接口描述语言(IDL),用于定义数据结构和消息格式。 它的设计目标是提供一种简单、高效、可扩展的方法来…...
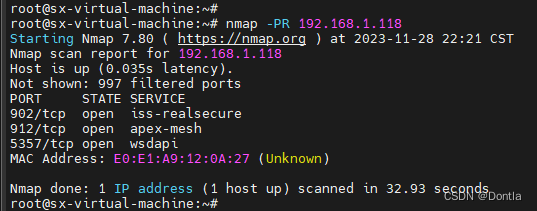
python-nmap库使用教程(Nmap网络扫描器的Python接口)(功能:主机发现、端口扫描、操作系统识别等)
文章目录 Python-nmap库使用教程前置条件引入python-nmap创建Nmap扫描实例执行简单的主机发现(nmap -sn)示例,我有一台主机配置为不响应 ICMP 请求,但使用nmap -sn,仍然能够探测到设备: 端口扫描扫描特定端…...
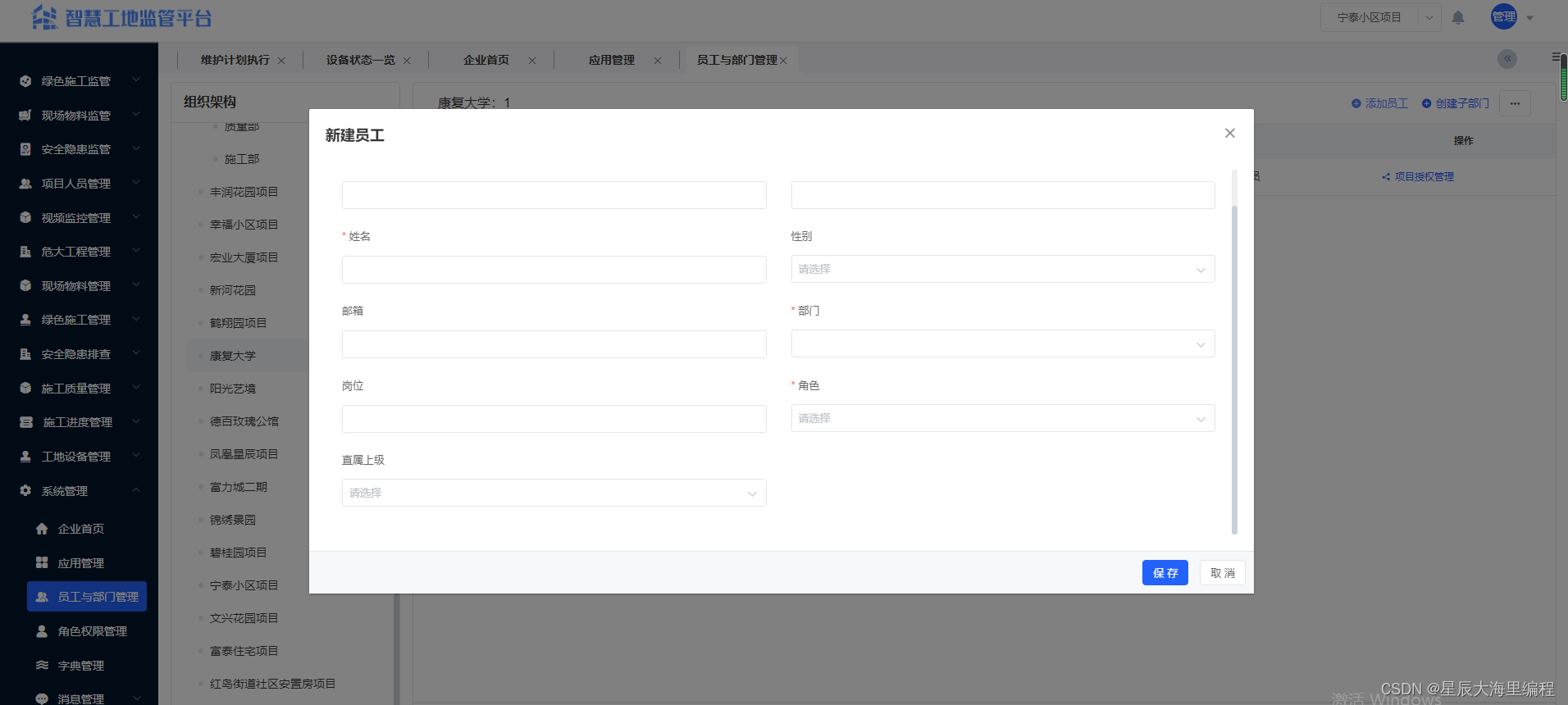
什么是智慧工地?
一、什么是智慧工地? 工地本身不拥有智慧,工地的运作是依赖于人的智慧。工地信息化技术,能够减少对人的依赖,使工地拥有智慧。 智慧工地,就是立足于“智慧城市”和“互联网”,采用云计算、大数据和物联网等…...
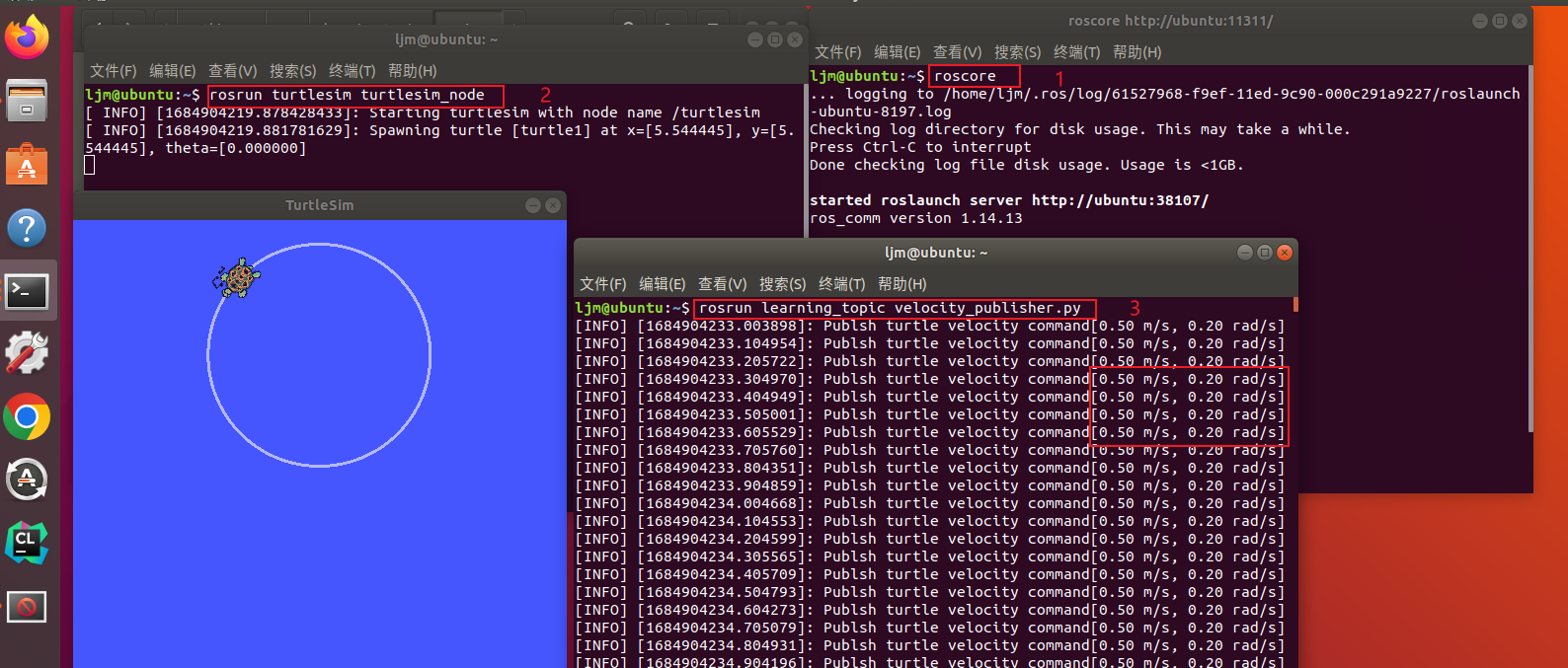
【古月居《ros入门21讲》学习笔记】08_发布者Publisher的编程实现
目录 说明: 1. 话题模型 图示 说明 2. 实现过程(C) 创建功能包 创建发布者代码(C) 配置发布者代码编译规则 编译并运行 编译 运行 3. 实现过程(Python) 创建发布者代码(…...

沿着马可·波罗的足迹,看数字云南
刚入行的时候,有位前辈跟我说过一句话:去现场“要像外国人一样去看”,重新审视那些自己可能早已“熟视无睹”的事物。 前不久,我跟随“看见数字云南——云南数字经济媒体探营活动”,奔赴昆明、大理、西双版纳等地&…...

记录问题-使用@Validated报错Validation failed for argument [0]
类字段 NotNull(message "双坐标不能为空", groups {Insert.class, Update.class})private Integer yAxisType;接口 /*** 添加** return*/RequestMapping(value "/add", method RequestMethod.POST)public Result add(Validated(Insert.class) Request…...

three.js--立方体
作者:baekpcyyy🐟 使用three.js渲染出可以调节大小的立方体 1.搭建开发环境 1.首先新建文件夹用vsc打开项目终端 2.执行npm init -y 创建配置文件夹 3.执行npm i three0.152 安装three.js依赖 4.执行npm I vite -D 安装 Vite 作为开发依赖 5.根…...

App的测试,和传统软件测试有哪些区别?应该增加哪些方面的测试用例?
从上图可知,测试人员所测项目占比中,App测试占比是最高的。 这就意味着学习期间,我们要花最多的精力去学App的各类测试。也意味着我们找工作前,就得知道,App的测试点是什么,App功能我们得会测试࿰…...
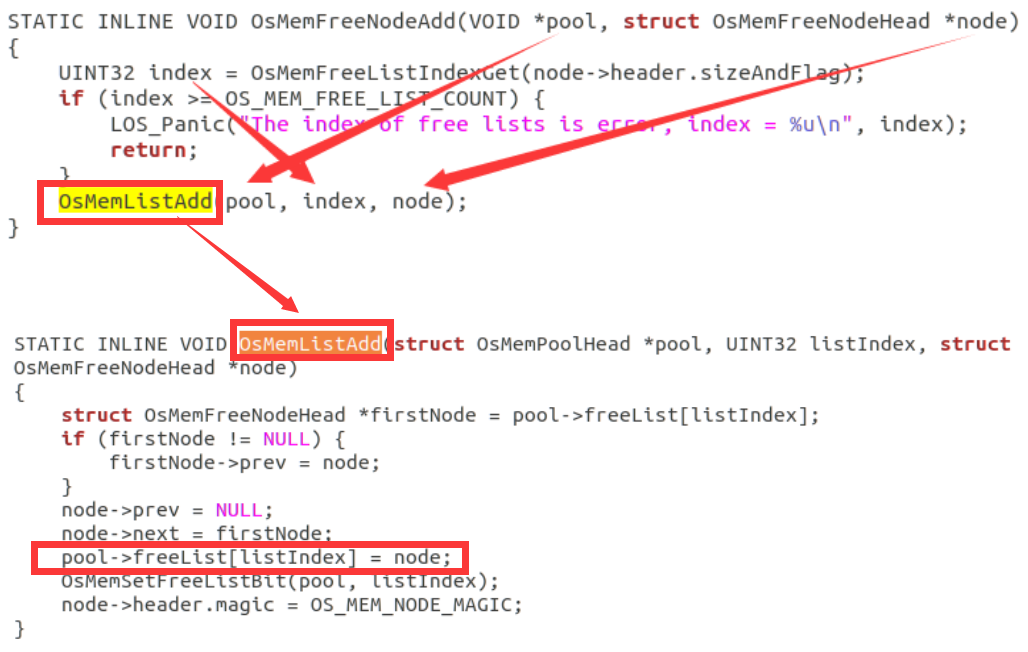
改进LiteOS中物理内存分配算法(详细实验步骤+相关源码解读)
一、实验要求 优化TLSF算法,将Best-fit策略优化为Good-fit策略,进一步降低时间复杂度至O(1)。 优化思路: 1.初始化时预先为每个索引中的内存块挂上若干空闲块,在实际分配时避免分割(split)操作ÿ…...
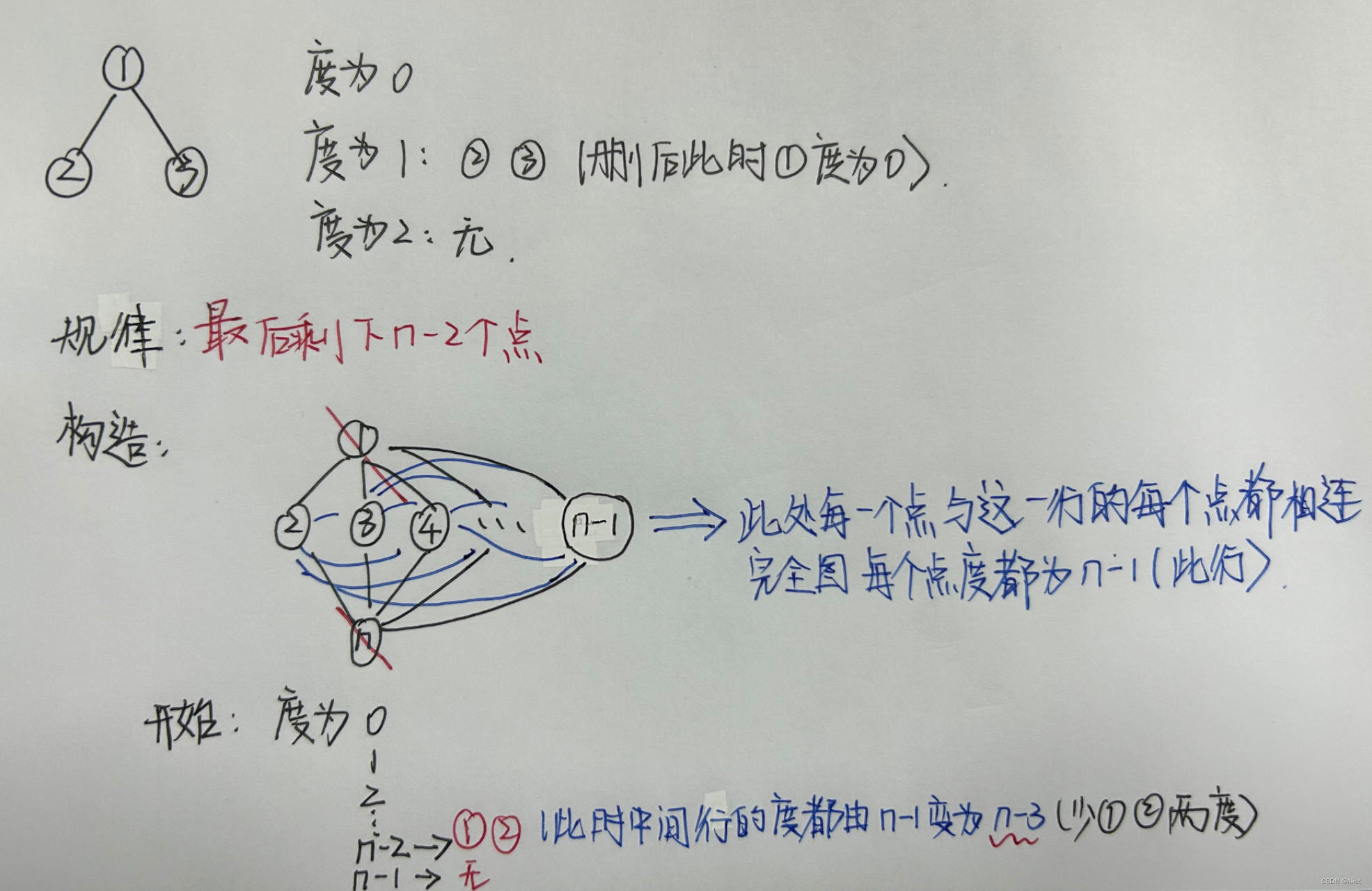
洛谷100题DAY8
36.P1416 攻击火星 此题找出规律即可 #include<bits/stdc.h> using namespace std; int n; int main() {cin >> n;cout << max(0, n - 2);return 0; } 37.P1551 亲戚 并查集模板题目 两个人如果使亲戚就合并建立联系,最后进行查找即可 #incl…...

2. OpenHarmony源码下载
OpenHarmony源码下载(windows, ubuntu) 现在的 OpenHarmony 4.0 源码已经有了,在 https://gitee.com/openharmony 地址中,描述了源码获取的方式。下来先写下 windows 的获取方式,再写 ubuntu 的获取方式。 获取源码前,还需要的准…...

flask app.config 用法
flask app.config flask app.config 是 Flask 应用程序的配置对象。它包含了 Flask 应用程序的所有配置信息,如数据库连接、密钥、调试模式等。 常用的 app.config 配置项如下: DEBUG:调试模式,默认为 False。 SECRET_KEY&…...
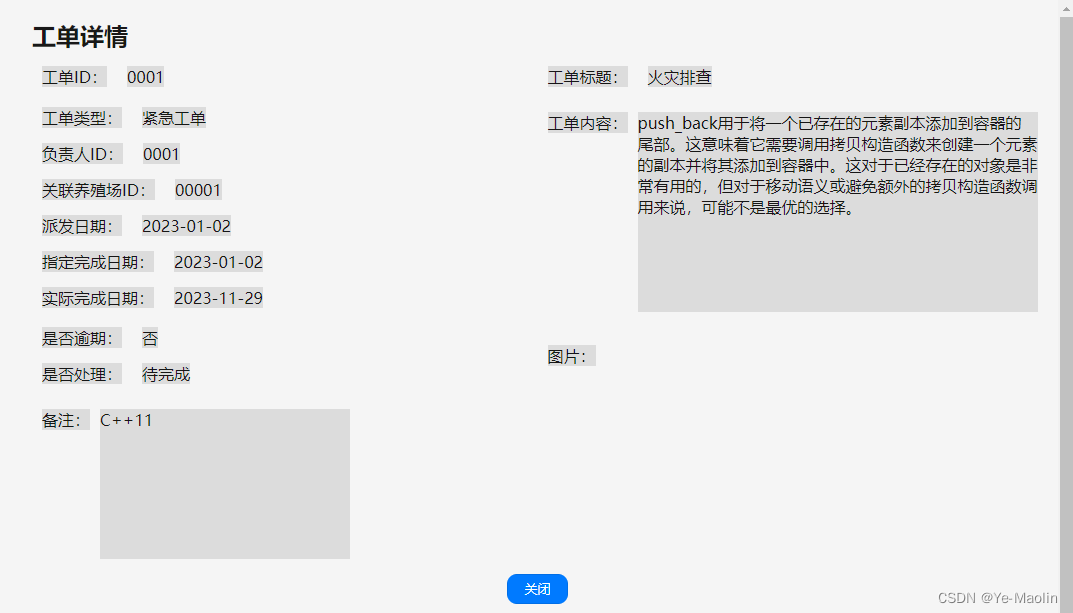
【Vue】【uni-app】实现工单列表项详情页面
这次主要实现的是一个工单详情页面 从工单列表项中点击详情 跳转到工单详情页面,这个详情页面就是这次我们要实现的页面,并可以通过点击这个关闭按钮返回到工单列表页面 首先是在我们原有的工单列表页面的按钮增加一个点击跳转 <button size"m…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
