关注这两点 或能避开一些现货黄金交易的陷阱
在现货黄金投资中,交易机会是处处都有,但是亏损的情况也可能出现。投资者要在陷阱处处的市场中获得稳定盈利,就需要懂得如何规避现货黄金投资的陷阱。下面我们就来介绍两个很常用的避开陷阱的方法。

看交易的活跃度。交易越活跃,市场出现陷阱的概率就越低。衡量活跃度一个很好用的指标是交易量,但是现货黄金投资中统计交易量是不太准确的,所以我们应该采取另外的方法来判断现货黄金的交易是否活跃,这个方法就是看K线。如果K线呈现出方向性的移动,例如是上涨或者下跌,且它们的K线不会太小,影线不会很长,这样就可以判断交易是较活跃的。如果当前金价没有明显的方向,而且盘面上都是小K线,还带有较长的影线,这就是交易不太活跃的时候,投资者应该尽量避免在交易不活跃的时候入场。
等待回撤。做现货黄金一个经典的陷阱就是交易突破。当现货黄金价格经过一段时间的调整后,向上或者向下突破横盘区间,很多投资者在这时候跟着突破方向入场,这就容易踩中陷阱,因为入场之后价格可能反转,至少也要等一波回撤。我们要避开这个陷阱,就不应该在突破发生的时候入场,应该先观察并等待回撤。
综上所述,在交易不活跃的时候别入场,当突破行情发生的时候,别急着跟突破方向入场,这样就能避免一些交易陷阱,希望以上内容对投资者会有所起伏。
相关文章:

关注这两点 或能避开一些现货黄金交易的陷阱
在现货黄金投资中,交易机会是处处都有,但是亏损的情况也可能出现。投资者要在陷阱处处的市场中获得稳定盈利,就需要懂得如何规避现货黄金投资的陷阱。下面我们就来介绍两个很常用的避开陷阱的方法。 看交易的活跃度。交易越活跃,市…...

Python 文件读写
Python 文件读写笔记整理 参数说明 open(path, flag[, encoding][,errors]) path:要打开文件的路径 flag:打开方式 encoding:编码方式 errors:错误处理 Flag打开方式表 模式 描述 r 以只读方式打开文件。文件的指针将会放在文件的开头。这是默认模式。 rb 以二进制格…...

线性分组码的奇偶校验矩阵均匀性分析
回顾信道编解码知识,我们知道信道编码要求编码具有检纠错能力,作为FEC(forward error correction)前向纠错编码的一类,线性分组码表示校验位与信息位的关系能够线性表示。 在这篇文章中,并不是要讨论信道编…...
leetcode算法之链表
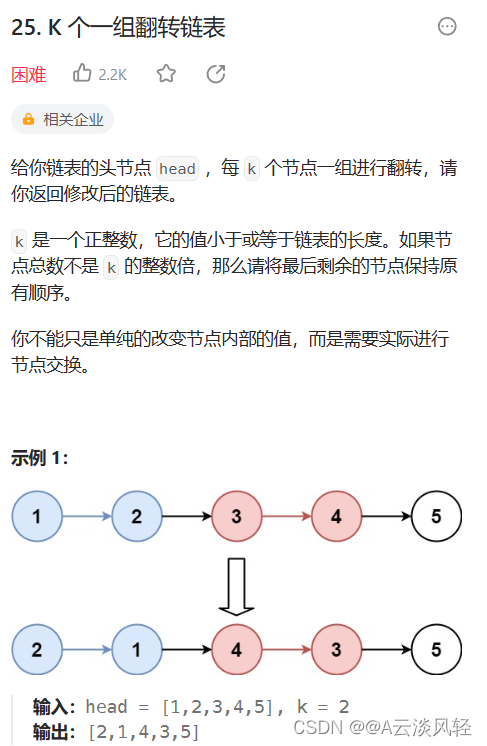
目录 1.两数相加2.两两交换链表中的节点3.重排链表4.合并K个升序链表5.K个一组翻转链表 1.两数相加 两数相加 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(…...

2023.11.27 滴滴P0级故障或为k8s升级造成
滴滴11.27 P0级故障|打车|宕机|网约车|出租车|滴滴出行|系统故障_网易订阅 (163.com) 如何看待滴滴11月27日故障,对日常生产生活有哪些影响? - 知乎 (zhihu.com) 最新消息滴滴P0故障原因,是由于k8s集群升级导致的,后面又进行版本…...
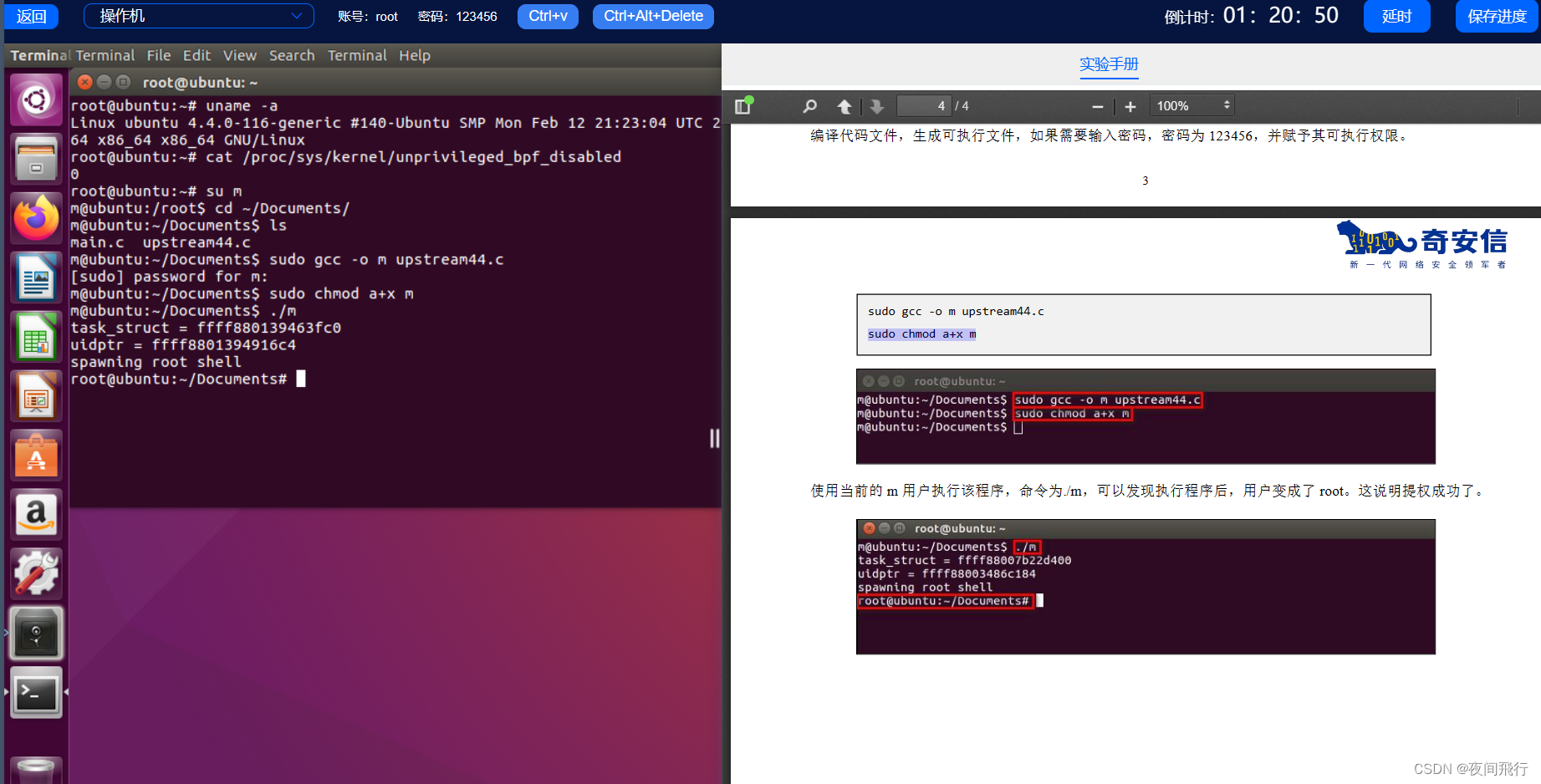
Ubuntu16.04.4系统本地提权实验
目录 1.介绍: 2.实验: 3.总结: 1.介绍: 1.1:eBPF简介:eBPF(extendedBerkeleyPacketFilter)是内核源自于BPF的一套包过滤机制,BPF可以理解成用户与内核之间的一条通道,有非常强大的…...

Vue中使用正则表达式进行文本匹配和处理的方法
1. 正则表达式基础 正则表达式是一种用来匹配字符串的模式。它由普通字符(例如字符 a 到 z)和特殊字符(称为"元字符")组成。以下是一些基本的正则表达式示例: 匹配邮箱的正则表达式: /^[\w-](\…...

php许愿墙代码包括前端和后端部分
以下是一个简单的PHP许愿墙代码示例,包括前端和后端部分: 前端HTML代码(index.html): <!DOCTYPE html> <html> <head><title>许愿墙</title> </head> <body><h1>许…...

PHP 刷新缓存区的问题!
PHP流式输出,在Nginx下可以正常刷新缓存区 , 但是在Apache下会等待循环全部执行完,才会刷新!有怎么解决? header(X-Accel-Buffering: no); // Nginx情况下必须加这一行header(Content-type: text/event-stream);header…...
Android Studio Giraffe-2022.3.1-Patch-3安装注意事项
准备工作: android studio下载地址:https://developer.android.google.cn/studio/releases?hlzh-cn gradle下载地址:https://services.gradle.org/distributions/ 比较稳定的网络环境(比较android studio相关的依赖需要从谷歌那边…...
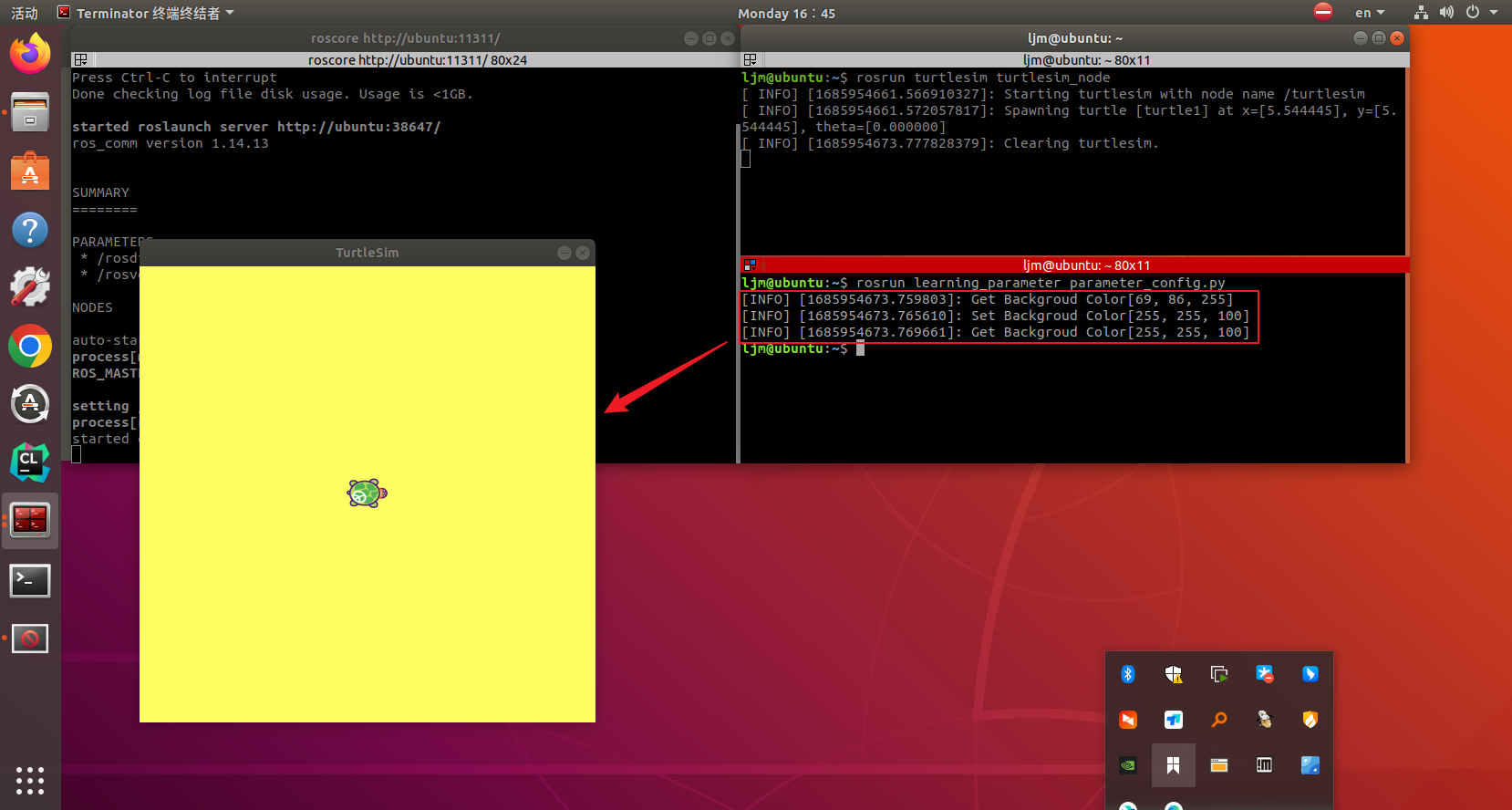
【古月居《ros入门21讲》学习笔记】14_参数的使用与编程方法
目录 说明: 1. 参数模型(全局字典) 2. 实现过程(C) 创建功能包 参数命令行的使用 YAML参数文件 rosparam命令 使用示例 编程方法(C) 配置代码编译规则 编译并运行 编译 运行 3. 实…...

Webpack 懒加载
文章目录 前言懒加载示例后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:webpack 🐱👓博主在前端领域还有很多知识和技术需要掌握,正在不断努力填补技术短板。(如果出现错误,感谢大家指出…...
深度遍历DFS(括号生成,二叉树所有路径)
正整数 n 代表生成括号的对数,请设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()","()(())","()()(…...

Rational Arithmetic
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️宝剑锋从磨砺出,梅花香自苦寒来 ☁️有理数运算 实现对两个有理数的…...
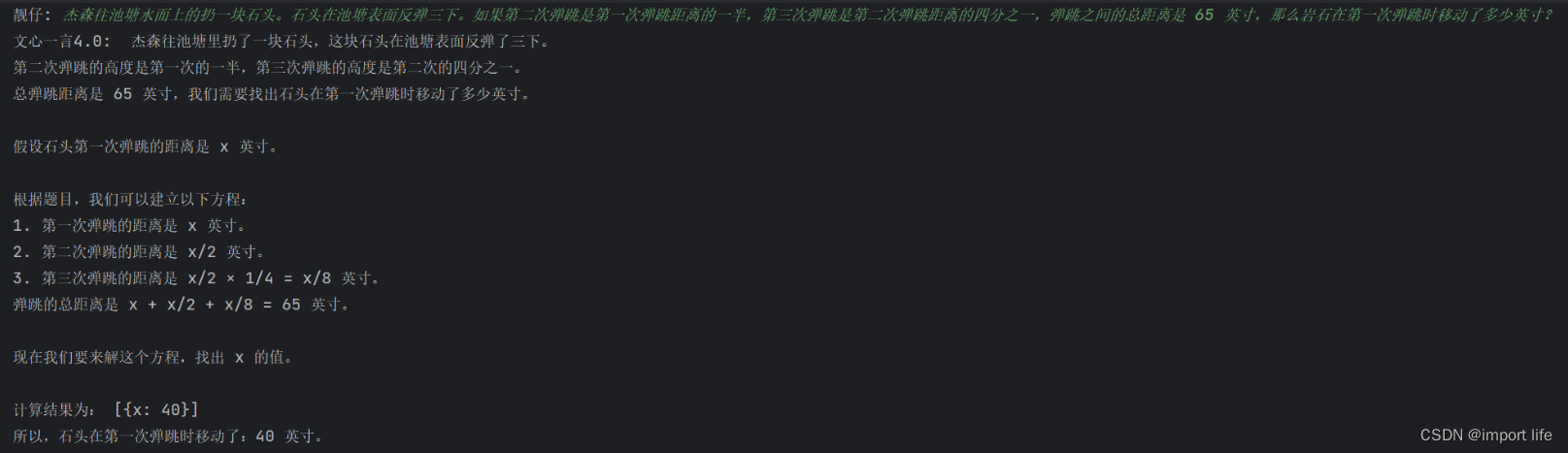
文心一言4.0(ERNIE-Bot-4)申请方法及简单调用代码示例
10月17日过后,估计很多人会看到类似的新闻,如图: 我看到这则新闻也是觉得非常感兴趣,于是本着“百闻不如一见”的实事求是的态度检索如何申请,没想到还真找到了ERNIE-Bot-4(俗称:文心一言4.0&a…...

年终好价节买什么好?这些数码好物闭眼入
大家是不是都没听说过好价节?直截了当地说,这其实就是原先的双十二购物狂欢节,只不过给它起了个新名字。不过,今年毕竟是首次改名,因此淘宝年终好价节的各种优惠,仍然是我们值得期待的!作为年前…...

webpack对项目进行优化
对项目进行优化是提高性能和效率的关键,以下是一些实用的Webpack优化技巧: 代码拆分(Code Splitting):将代码拆分为多个小块,按需加载。通过配置splitChunks插件,可以将公共代码提取到单独的文件…...

Python edge-tts库全部声音模型一览表
下面是edge-tts的声音模型,zh-CN为中文语音模型 Name: af-ZA-AdriNeural Gender: Female Name: af-ZA-WillemNeural Gender: Male Name: am-ET-AmehaNeural Gender: Male Name: am-ET-MekdesNeural Gender: Female Name: ar-AE-FatimaNeural Gender: Female N…...

网络编程相关面试题
目录 1.请解释一下什么是TCP协议的三次握手?2.TCP协议使用什么机制确保数据包的顺序和完整性?3.什么是UDP协议?它与TCP协议有什么不同?4.请解释一下什么是IP地址?为什么需要它?5.请解释一下什么是端口&…...

TCP_NODELAY与TCP通信效率
最近做tcp通信速度测试:主要流程如下所示: //client: while() { send data... recv data... //阻塞 }//server: while() { recv data... send data... } 当每次send数据量较小时,速度极慢!而send数据量较大时速度尚可。两者速度…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
