当前位置： 首页 > news >正文

java基础面试题(二)

news 2026/2/4 20:45:15

java后端面试题大全

  • 3.JVM
    • 3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置?
    • 3.2 java类的加载流程
    • 3.3 java内存溢出什么时候会发生以及解决方法

3.JVM

3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置?

  • 堆
    对象实例、String常量池、基本类型常量池、静态变量
  • 方法区
    类信息、类常量池、运行时常量池
  • 虚拟机栈
    临时变量

3.2 java类的加载流程

java文件到最终运行, 需要经过编译和类加载这两个阶段
编译的过程:把.java文件编译成.class文件
类加载的过程:把.class文件加载到jvm的内存中

  1. 加载
    通过类的全限定名获取类的二进制数据, 这可以通过类加载器完成, 类加载器可以从文件系统、网络、ZIP文件等地方获取类文件的二进制数据
    将获取的二进制数据转换为方法区（或元空间）的运行时数据结构, 这个数据结构存储了类的字段、方法、构造方法等信息，同时也包含了类的常量池，即字面量（如字符串、final常量）和符号引用等。
  2. 验证
    确保被加载的类的正确性. 这个阶段主要包括文件格式验证、元数据验证、字节码验证等，以确保类文件的正确性和安全性。
  3. 准备
    为类的静态变量分配内存并设置初始值, 这里的初始值通常是默认值，比如数值类型的默认值是0，引用类型的默认值是null
  4. 解析
    类、接口、字段和方法的符号引用解析为直接引用
  5. 初始化
    类的初始化方法

3.3 java内存溢出什么时候会发生以及解决方法

一、内存溢出的原因
如果内存泄露的空间足够大，就会导致内存溢出

堆内存中一个对象不再使用时，垃圾回收器却无法从内存中删除他们，导致内存泄露。

二、内存泄露的影响

相关文章：

java基础面试题(二)

java后端面试题大全 3.JVM3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置?3.2 java类的加载流程3.3 java内存溢出什么时候会发生以及解决方法 3.JVM 3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置? 堆 对象实例、String常量池、基…...

编程日记 2023/12/1 7:58:43

php爬虫实现把目标页面变成自己的网站页面

最近又被烦的不行，琐事不断，要是比起懒来一个人比一个人懒，但是懒要转换成动力啊，能让自己真正的偷懒，而不是浪费时间。每天还是需要不断的学习的，才能更好的提高效率，把之前做的简单小功能爬虫…...

编程日记 2023/12/1 7:57:42

[c语言c++]手写你自己的swap交换函数

函数传参有按值传递，指针传递，引用传递，分别看一下三种情况下的交换函数如何书写，应该使用哪种最方便。 当书写一个交换两个值的 swap 函数时，我们可以分别使用按值传参、指针传参和引用传参的方式来实现。下面是示例和…...

编程日记 2023/12/1 7:56:42

技术类知识汇总（二）

在自己日常学习javaweb的过程中，做的一些笔记和总结，汇总如下： Springboot项目的静态资源(html，css，js等前端资源)默认存放目录为：classpath:/static classpath:/public classpath:/resources"三层架…...

编程日记 2023/12/1 7:55:40

简单好用！日常写给 ChatGPT 的几个提示词技巧

ChatGPT 很强，但是有时候又显得很蠢，下面是使用 GPT4 的一个实例： 技巧一：三重冒号 """ 引用内容使用三重冒号 """，让 ChatGPT 清晰引用的内容： 技巧二：角色设定…...

编程日记 2023/12/1 7:52:36

pytorch分布式训练

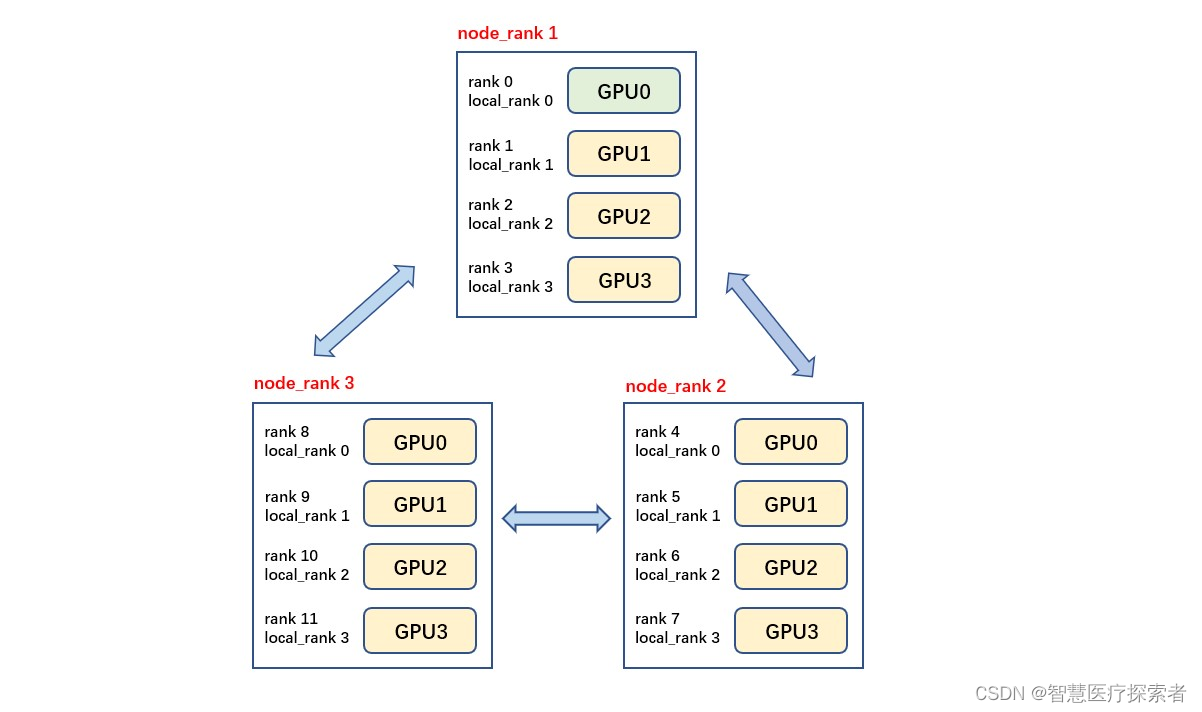
1 基本概念 rank：进程号，在多进程上下文中，我们通常假定rank 0是第一个进程或者主进程，其它进程分别具有1，2，3不同rank号，这样总共具有4个进程 node：物理节点，可以是一个…...

编程日记 2023/12/1 7:51:35

【PyTorch】（三）模型的创建、参数初始化、保存和加载

文章目录 1. 模型的创建1.1. 创建方法1.1.1. 通过使用模型组件1.1.2. 通过继承nn.Module类 1.2. 模型组件1.2.1. 网络层1.2.2. 函数包1.2.3. 容器 1.3. 将模型转移到GPU 2. 模型参数初始化3. 模型的保存与加载3.1. 只保存参数3.2. 保存模型和参数 1. 模型的创建 1.1. 创建方法…...

编程日记 2023/12/1 7:48:29

高效开发之：判断复杂list中的对象属性是否包含某个值

技术使用&#xff1a;使用了Java 8引入的Stream API以及Optional类。这些特性用于简化集合的处理和减少空指针异常。 List<ResourceInfoDto> authData chatBase.getData();String baseName dto.getBaseName();Optional<ResourceInfoDto> authWithResourceCode a…...

编程日记 2023/12/1 7:47:28

MacOS + Android Studio 通过 USB 数据线真机调试

环境&#xff1a;Apple M1 MacOS Sonoma 14.1.1 软件&#xff1a;Android Studio Giraffe | 2022.3.1 Patch 3 设备&#xff1a;小米10 Android 13 一、创建测试项目 安卓 HelloWorld 项目: 安卓 HelloWorld 项目 二、数据线连接手机 1. 手机开启开发者模式 参考&#xff1…...

编程日记 2023/12/1 7:46:26

部署jekins遇到的问题

jdk问题 我用的jdk版本是21的结果版本太新了&#xff0c;启动jekins服务的时候总是报错最后在jekins的安装目录下面的jekinsErr.log查看日志发现是jdk问题最后换了一个17版本的就解决了。 unity和jekins jekins和Git源码管理 jekins和Git联动使用 我想让jekins每次打包的时…...

编程日记 2023/12/1 7:45:25

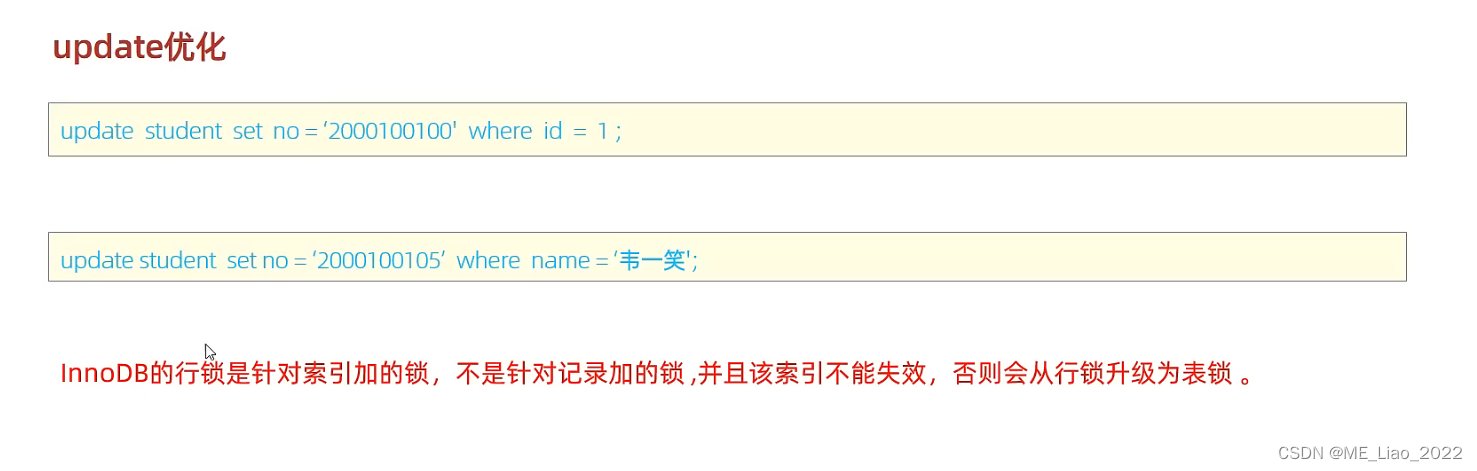
SQLY优化

insert优化 1.批量插入 手动事务提交 主键顺序插入&#xff0c;主键顺序插入性能高于乱序插入 2.大批量插入数据 如果一次性需要插入大批量数据&#xff0c;使用Insert语句插入性能较低&#xff0c;此时可以使用MYSQL数据库提供的load指令进行插入 主键优化 主键设计原则 …...

编程日记 2023/12/1 7:44:21

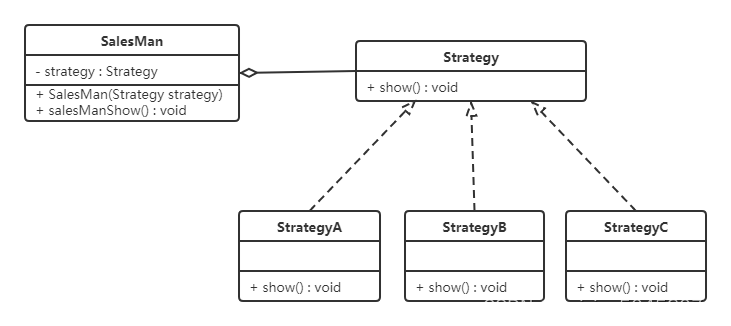
设计模式——行为型模式（一）

行为型模式用于描述程序在运行时复杂的流程控制，即描述多个类或对象之间怎样相互协作共同完成单个对象都无法单独完成的任务，它涉及算法与对象间职责的分配。 行为型模式分为类行为模式和对象行为模式，前者采用继承机制来在类间分派行为，后者采用组合或聚合在对象间分配行…...

编程日记 2023/12/1 7:42:19

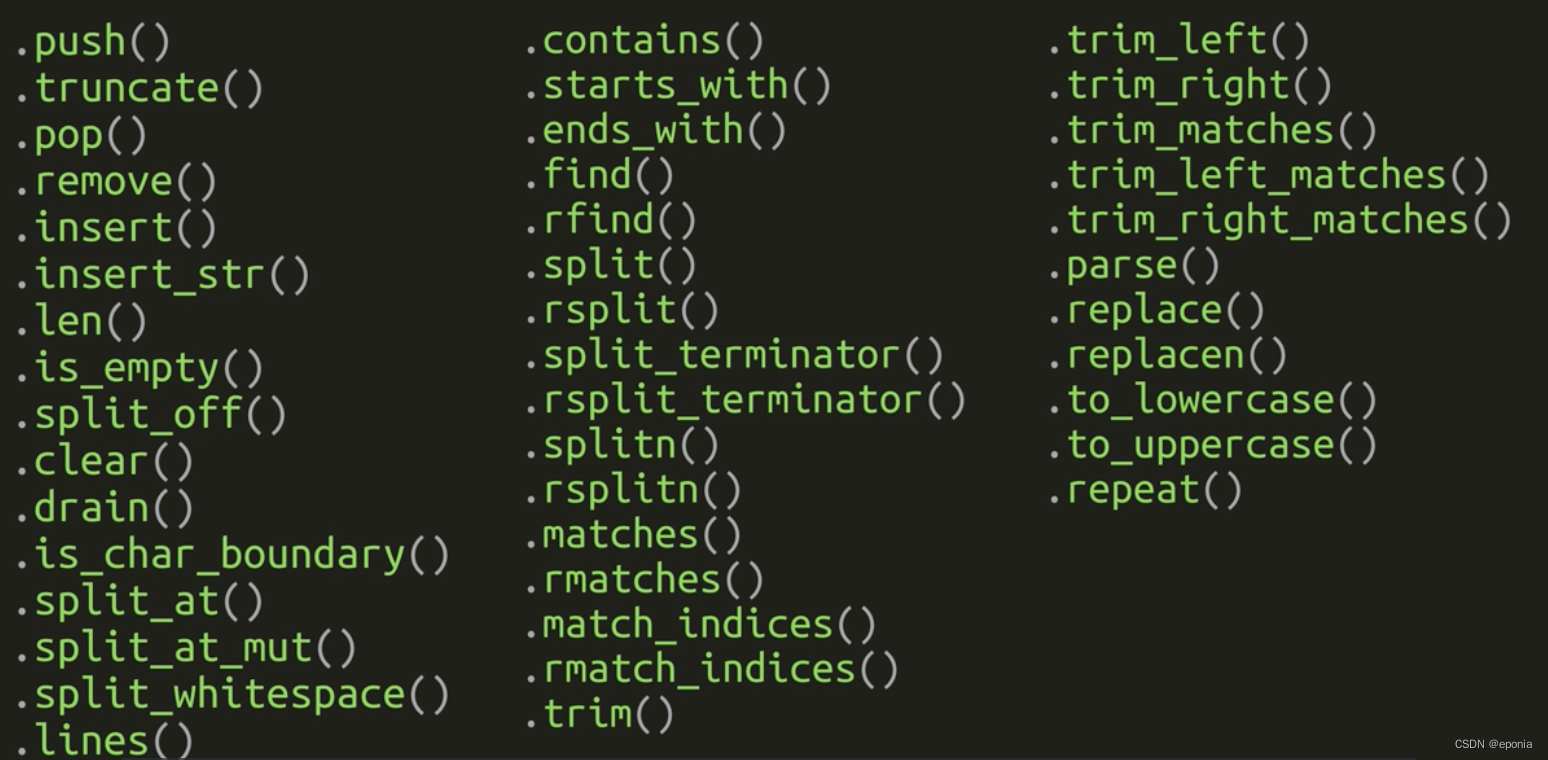
Rust语言入门教程(六) - 字符串类型

在Rust中&#xff0c; 字符串类型其实是一个比较复杂的话题。在Rust的标准库中&#xff0c;至少都提供了6种字符串类型&#xff0c;我们平常使用的最多的是其中的两种。这两种类型互相之间也有所关联&#xff1a; str&#xff1a; 字符串切片String 字符串 其中&#xff0c; 字…...

编程日记 2023/12/1 7:41:17

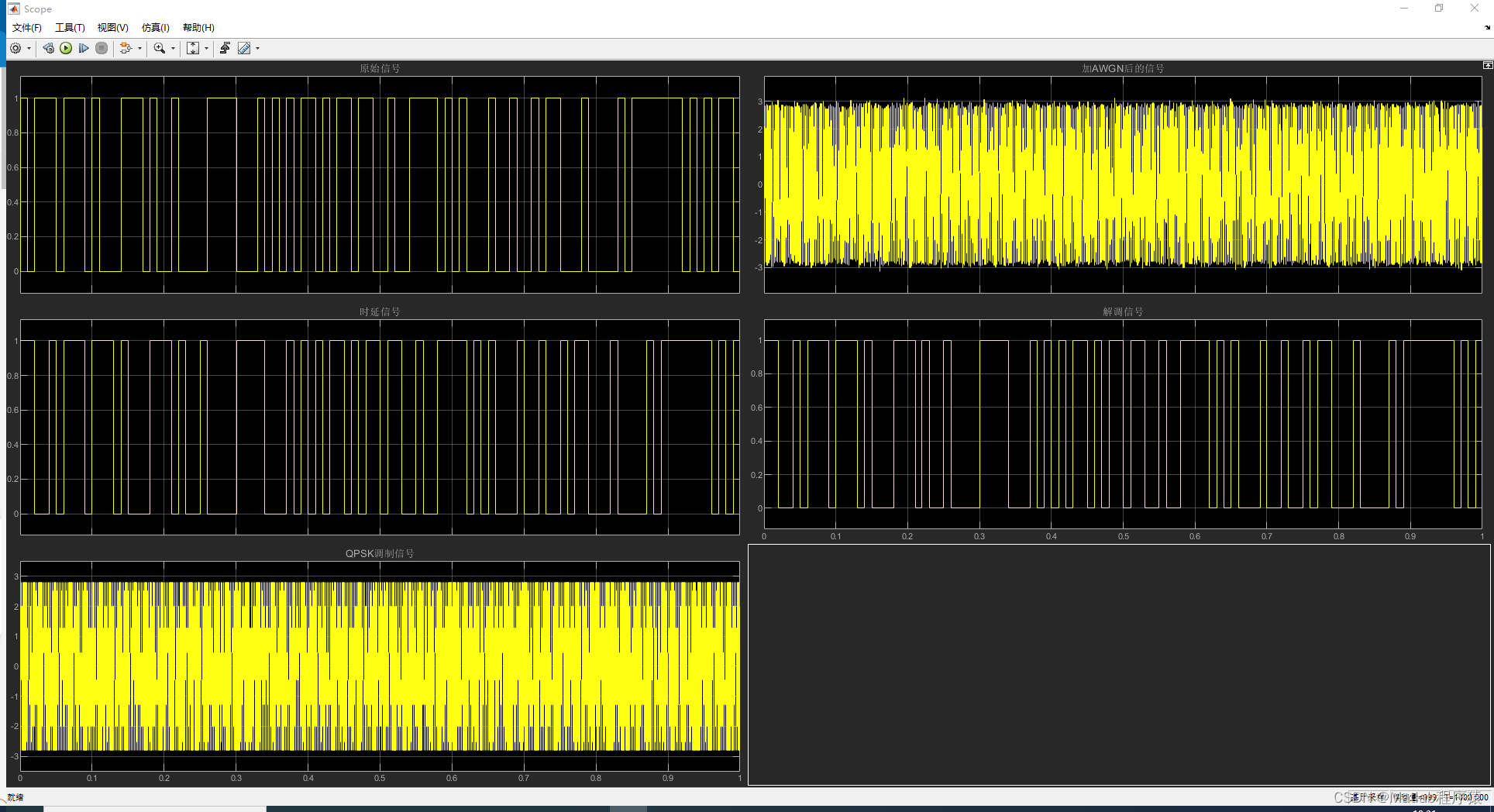
【MATLAB源码-第92期】基于simulink的QPSK调制解调仿真，采用相干解调对比原始信号和解调信号。

操作环境&#xff1a; MATLAB 2022a 1、算法描述 QPSK&#xff0c;有时也称作四位元PSK、四相位PSK、4-PSK&#xff0c;在坐标图上看是圆上四个对称的点。通过四个相位&#xff0c;QPSK可以编码2位元符号。图中采用格雷码来达到最小位元错误率&#xff08;BER&#xff09; —…...

编程日记 2023/12/1 7:40:16

关于C语言控制浮点数输出精度问题

众所周知 C语言在控制一个浮点数输出精度的时候是在%和f之间加上一个.(想要控制的精度) 如&#xff1a;printf("%.2f", num); 问&#xff0c;试问&#xff1a;&#xff08;你就是我的御主吗&#xff1f;&#xff09;如果输出的精度是根据输入的数字变化的怎么办&am…...

编程日记 2023/12/1 7:39:13

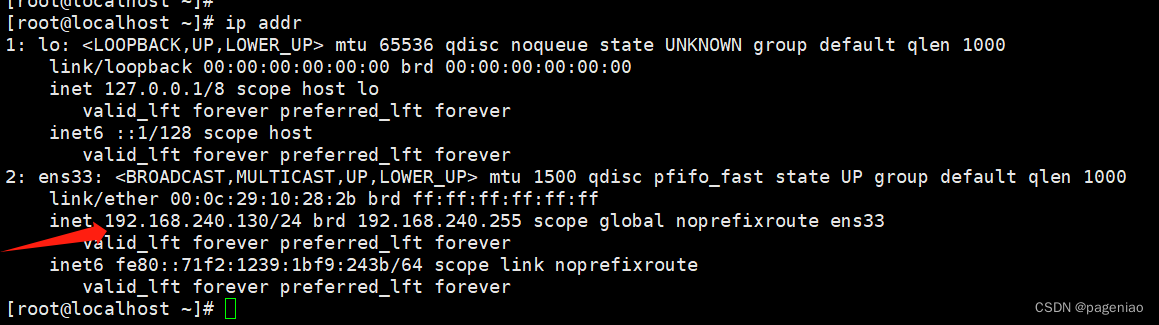
【Linux 静态IP配置】

静态IP配置 1.NAT模式设置2.设置静态ip3.重启网络4.查看ip 1.NAT模式设置 首先设置虚拟机中NAT模式的选项&#xff0c;打开VMware&#xff0c;点击“编辑”下的“虚拟网络编辑器”&#xff0c;设置NAT参数 注意&#xff1a; VMware Network Adapter VMnet8保证是启用状态 …...

编程日记 2023/12/1 7:38:13

【Linux 操作系统配置 SFTP】

Linux 操作系统配置 SFTP sftp采用的是ssh加密隧道&#xff0c;安装性方面较ftp强&#xff0c;而且依赖的是系统自带的ssh服务&#xff0c;不像ftp还需要额外的进行安装基于 ssh 的 sftp 服务相比 ftp 有更好的安全性&#xff08;非明文帐号密码传输&#xff09;和方便的权限管…...

编程日记 2023/12/1 7:37:10

信贷专员简历模板

这份简历内容&#xff0c;以信贷专员招聘需求为背景&#xff0c;我们制作了1份全面、专业且具有参考价值的简历案例&#xff0c;大家可以灵活借鉴。 信贷专员简历在线编辑下载&#xff1a;百度幻主简历 求职意向 求职类型&#xff1a;全职 意向岗位&#xff1a;信贷专员 …...

编程日记 2023/12/1 7:35:06

Python自动化测试面试经典题

相信大家经历过许多面试都会有这样的感受&#xff1a;好不容易通过了 2 -3轮技术面试&#xff0c;但是薪资不够理想&#xff1b;要么被面试的测试专家虐的不要不要的。但每一次的面试也能让自己认识到不足之处&#xff0c;这样才有利于后续拿到理想的offer。 牛鹭学院的学子对…...

编程日记 2023/12/1 7:34:05

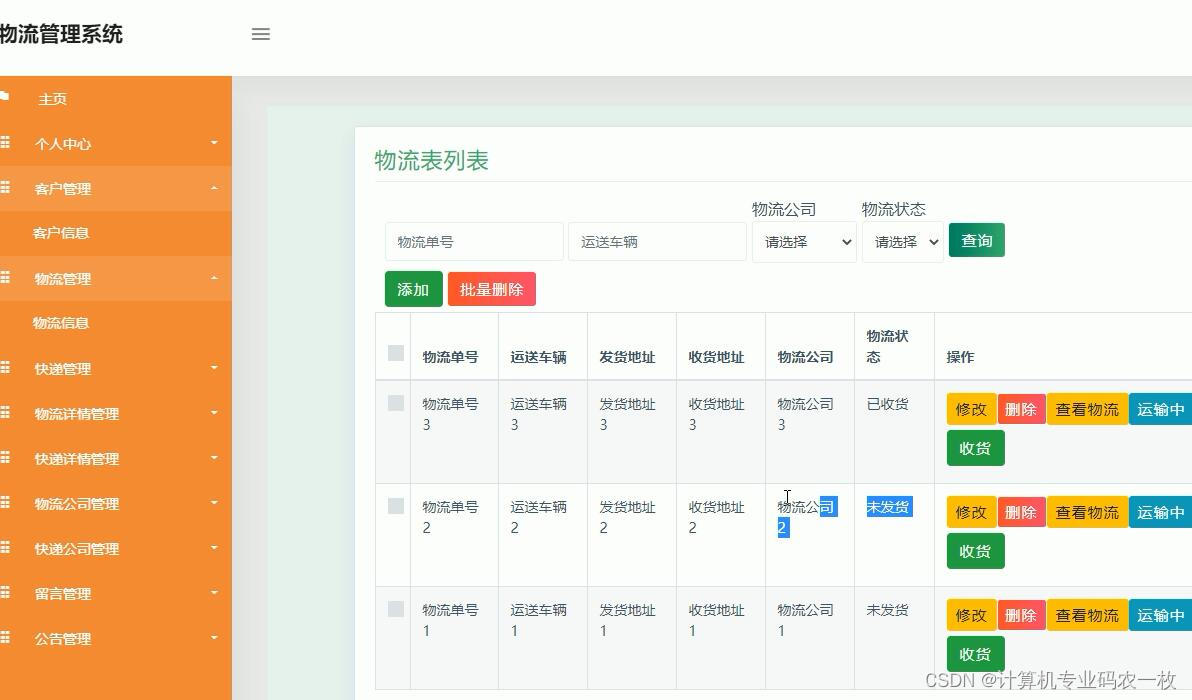
java+springboot物流管理系统设计与实现wl-ssmj+jsp

物流管理系统的开发和综合性的物流信息网站平台的建设。研究的重点是运输管理信息系统&#xff0e;本系统是一套基于运输作业流程的管理系统&#xff0c;该系统以运输任务、货品、商务三大线索设计开发。运输任务是该管理系统的核心&#xff0c;系统通过对运输任务中的接收、调…...

编程日记 2023/12/1 7:32:03

8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂

蛋白质结合剂&#xff08;如抗体、抑制肽&#xff09;在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上&#xff0c;高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术&#xff0c;但这类方法普遍面临资源消耗巨大、研发周期冗长…...

编程新知 2026/1/25 13:18:12

376. Wiggle Subsequence

376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

编程新知 2026/1/26 1:54:23

从零开始打造 OpenSTLinux 6.6 Yocto 系统（基于STM32CubeMX）（九）

设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile&#xff0c;新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

编程新知 2026/1/31 11:35:18

Angular微前端架构：Module Federation + ngx-build-plus (Webpack)

以下是一个完整的 Angular 微前端示例&#xff0c;其中使用的是 Module Federation 和 npx-build-plus 实现了主应用&#xff08;Shell&#xff09;与子应用&#xff08;Remote&#xff09;的集成。 &#x1f6e0;️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

编程新知 2025/12/3 10:52:37

C++.OpenGL （14/64）多光源（Multiple Lights）

多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

编程新知 2025/6/11 3:15:20

快刀集(1): 一刀斩断视频片头广告

一刀流&#xff1a;用一个简单脚本&#xff0c;秒杀视频片头广告&#xff0c;还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农&#xff0c;平时写代码之余看看电影、补补片&#xff0c;是再正常不过的事。 电影嘛&#xff0c;要沉浸&#xff0c;…...

编程新知 2026/1/8 0:40:27

python爬虫——气象数据爬取

一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用&#xff1a; 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests&#xff1a;发送 …...

编程新知 2025/12/16 7:53:39

rknn toolkit2搭建和推理

安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 &#xff0c;不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源&#xff08;最常用&#xff09; conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

编程新知 2026/1/20 9:52:37

篇章二 论坛系统——系统设计

目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

编程新知 2026/2/1 0:38:28

WebRTC调研

WebRTC是什么&#xff0c;为什么&#xff0c;如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

编程新知 2026/2/3 20:21:30