全志XR806基于FreeRTOS下部署竞技机器人先进模糊控制器
前言
- 很荣幸参与到由“极术社区和全志在线联合组织”举办的XR806开发板试用活动。
- 本人热衷于各种的开发板的开发,同时更愿意将其实现到具体项目中。
- 秉承以上原则,发现大家的重心都放在开发中的环境构建过程,缺少了不少实际应用场景的运用,虽然环境搭建确实痛苦。本文主要使用XR806的FreeRTOS到实际的机器人控制应用中,并实现部署模糊控制器。
- 环境搭建本文简要略写,大家可以看社区其它优秀的文章。
- 文章中应用到的无线控制和多维状态机两个重要的开发应用,会在后面的文章中陆续更新。
使用环境
1.本人使用window10+VMware+ubuntu 18.04 这里不多阐述
2.按照官方文档移植XR806的FreeRTOS
项目介绍
基于XR806——FreeRTOS为项目主控,部署先进模糊控制器,实现对于竞技机器人的机构控制和定位控制等。


软硬件框架

控制部署
继电推理
在封装好电机驱动电流环时,实现对电机的控制,相当于建立了一种
继电特性的非线性控制,此时使用继电整定法的Z-N临界比例度法去建立模糊域。
根据以下临界系数表,整定求出模糊域。
| 控制器类型 | KP | Tn | Tv | Ki | Kd |
|---|---|---|---|---|---|
| P | 0.5*Kμ | — | — | — | — |
| PD | 0.8*Kμ | — | 0.12*Tμ | — | KP*Tn |
| PI | 0.45*Kμ | 0.85*Tμ | — | KP/Tn | — |
| PID | 0.6*Kμ | 0.5*Tμ | 0.12*Tμ | KP/ Tn | KP*Tn |
模糊推理
模糊推理的核心就是计算出E和EC的隶属度。同时把E和EC分为多种子集情况:负最大NB,负中NM,负小NS,零ZO,正小PS,正中PM,正大PB等七种情况。然后计算E/EC种子集的隶属度。
清晰化
进行模糊推理后,可以根据计算的隶属度,建立模糊规则表,实现对输出值的清晰化。对应到应用层的输出函数,实现控制输出。
例图:

FOC控制

仿真效果


代码实现
以下提供部分代码:
自动整定
void PID_AutoTune_Task(void)
{if(pid.AutoRegurating_Status != START) return;/*定义临界Tc*/float Tc = 0.0;static int start_cnt; //记录最大值出现的时间static int end_cnt; //记录周期结束时的时间值 static uint16_t cool_cnt = 0; static uint16_t heat_cnt = 0;// pid.Autotune_Cnt ++; //计数if((pid.Pv_position == UP) && (pid.Pv < pid.Sv)) {cool_cnt ++;if(cool_cnt >= 3) //连续三次都越过,则说明真的越过了{pid.Pv_position = DOWN; //标记当前在下方了pid.Zero_Across_Cnt ++; //标记穿越一次cool_cnt = 0;}}else if((pid.Pv_position == DOWN)&&(pid.Pv > pid.Sv))//刚才在下方,现在在上方{heat_cnt++;if(heat_cnt >= 3) //连续三次都越过,则说明真的越过了{pid.Pv_position = UP; //标记当前在下方了pid.Zero_Across_Cnt ++; //标记穿越一次heat_cnt = 0;} }/*****************开始计算强行振荡的周期****************************/ if((pid.Zero_Across_Cnt == 2)&&(start_cnt == 0)){start_cnt = pid.Autotune_Cnt;printf("start_time = %d\r\n", start_cnt);}else if((pid.Zero_Across_Cnt == 4)&&(end_cnt == 0)){end_cnt = pid.Autotune_Cnt;printf("start_time = %d\r\n", end_cnt);}if(pid.Zero_Across_Cnt == 4){ /*计算一个震荡周期的时间*/if(start_cnt > end_cnt)Tc = (start_cnt-end_cnt)/2; elseTc = (end_cnt-start_cnt)/2; /*计算Kp,Ti和Td*/pid.Kp = 0.6*pid.Kp;pid.Ti = Tc*0.5; pid.Td = Tc*0.12; /*PID参数整定完成,将各项数据清0*/heat_cnt = 0;cool_cnt = 0; pid.Autotune_Cnt = 0;start_cnt = 0;end_cnt = 0; pid.SEk = 0;pid.Zero_Across_Cnt = 0; pid.AutoRegurating_EN = OFF;pid.AutoRegurating_Status = OVER; //开始运行使用新的参数后的PID算法pid.Sv = pid.BKSv; }
}
模糊控制
/*模糊规则表*/
int KpRule[7][7]= { /*NB, NM, NS, ZO, PS, PM, PB -EC*/{1, 1, 1, 1, 1, 1, 1}, //NB 0~-10{0, 0, 0, 1, 2, 3, 4}, //NM 0~10{0, 0, 0, 1, 2, 3, 4}, //NS 10~20 {0, 0, 1, 1, 2, 3, 4}, //20~30{1, 1, 1, 1, 2, 3, 4}, //30~40{1, 1, 1, 1, 2, 3, 4}, //40 ~50{6, 6, 6, 6, 6, 6, 6}, //50~60
};
static float fuzzy_kp(float err, float errchange)
{ volatile float Kp_calcu; volatile uint8_t num,pe,pec; volatile float eFuzzy[2]={0.0,0.0}; //隶属于误差E的隶属程度 volatile float ecFuzzy[2]={0.0,0.0}; //隶属于误差变化率EC的隶属程度 float KpFuzzy[7]={0.0,0.0,0.0,0.0,0.0,0.0,0.0}; //隶属于Kp的隶属程度 /*****误差E隶属函数描述*****/ if(err<eRule[0]) { eFuzzy[0] =1.0; pe = 0; } else if(eRule[0]<=err && err<eRule[1]) { eFuzzy[0] = (eRule[1]-err)/(eRule[1]-eRule[0]); pe = 0; } else if(eRule[1]<=err && err<eRule[2]) { eFuzzy[0] = (eRule[2] -err)/(eRule[2]-eRule[1]); pe = 1; } else if(eRule[2]<=err && err<eRule[3]) { eFuzzy[0] = (eRule[3] -err)/(eRule[3]-eRule[2]); pe = 2; } else if(eRule[3]<=err && err<eRule[4]) { eFuzzy[0] = (eRule[4]-err)/(eRule[4]-eRule[3]); pe = 3; } else if(eRule[4]<=err && err<eRule[5]) { eFuzzy[0] = (eRule[5]-err)/(eRule[5]-eRule[4]); pe = 4; } else if(eRule[5]<=err && err<eRule[6]) { eFuzzy[0] = (eRule[6]-err)/(eRule[6]-eRule[5]); pe = 5; } else { eFuzzy[0] = 0.0; pe = 6; } eFuzzy[1] =1.0 - eFuzzy[0]; /*****误差变化率EC隶属函数描述*****/ if(errchange<ecRule[0]) { ecFuzzy[0] =1.0; pec = 0; } else if(ecRule[0]<=errchange && errchange<ecRule[1]) { ecFuzzy[0] = (ecRule[1] - errchange)/(ecRule[1]-ecRule[0]); pec = 0 ; } else if(ecRule[1]<=errchange && errchange<ecRule[2]) { ecFuzzy[0] = (ecRule[2] - errchange)/(ecRule[2]-ecRule[1]); pec = 1; } else if(ecRule[2]<=errchange && errchange<ecRule[3]) { ecFuzzy[0] = (ecRule[3] - errchange)/(ecRule[3]-ecRule[2]); pec = 2 ; } else if(ecRule[3]<=errchange && errchange<ecRule[4]) { ecFuzzy[0] = (ecRule[4]-errchange)/(ecRule[4]-ecRule[3]); pec=3; } else if(ecRule[4]<=errchange && errchange<ecRule[5]) { ecFuzzy[0] = (ecRule[5]-errchange)/(ecRule[5]-ecRule[4]); pec=4; } else if(ecRule[5]<=errchange && errchange<ecRule[6]) { ecFuzzy[0] = (ecRule[6]-errchange)/(ecRule[6]-ecRule[5]); pec=5; } else { ecFuzzy[0] =0.0; pec = 5; } ecFuzzy[1] = 1.0 - ecFuzzy[0]; /*********查询模糊规则表*********/ num = KpRule[pe][pec]; KpFuzzy[num] += (eFuzzy[0]*ecFuzzy[0]); num = KpRule[pe][pec+1]; KpFuzzy[num] += (eFuzzy[0]*ecFuzzy[1]); num =KpRule[pe+1][pec]; KpFuzzy[num] += (eFuzzy[1]*ecFuzzy[0]); num = KpRule[pe+1][pec+1]; KpFuzzy[num] += (eFuzzy[1]*ecFuzzy[1]); /*********加权平均法解模糊*********/ Kp_calcu = KpFuzzy[0]*kpRule[0] +KpFuzzy[1]*kpRule[1]+ \KpFuzzy[2]*kpRule[2] +KpFuzzy[3]*kpRule[3]+ \KpFuzzy[4]*kpRule[4] +KpFuzzy[5]*kpRule[5]+ \+KpFuzzy[6]*kpRule[6]; printf(" %f,%f,%d,%d,kp = %f\r\n", err, errchange, pe, pec, Kp_calcu);return(Kp_calcu);
}
实物展示
无刷电机控制
https://www.bilibili.com/video/BV1FN4y1C7fY/?aid=874778769&cid=1302701130&page=null
整体定位控制
https://www.bilibili.com/video/BV1NN411t7Fy/?aid=492262076&cid=1302702003&page=null
以上,就是本文分享的全部内容了,感谢各位
相关文章:

全志XR806基于FreeRTOS下部署竞技机器人先进模糊控制器
前言 很荣幸参与到由“极术社区和全志在线联合组织”举办的XR806开发板试用活动。本人热衷于各种的开发板的开发,同时更愿意将其实现到具体项目中。秉承以上原则,发现大家的重心都放在开发中的环境构建过程,缺少了不少实际应用场景的运用&am…...

python动态加载内容抓取问题的解决实例
问题背景 在网页抓取过程中,动态加载的内容通常无法通过传统的爬虫工具直接获取,这给爬虫程序的编写带来了一定的技术挑战。腾讯新闻(https://news.qq.com/)作为一个典型的动态网页,展现了这一挑战。 问题分析 动态…...

系列二十三、将一个第三方的类配置成bean的方式
一、将一个第三方的类配置成bean的方式 1.1、概述 日常的JavaEE开发中,难免不会遇到需要使用第三方的类的情况,比如:MyBatisPlus、RedisTemplate、DruidDataSource...,这些外部组件是不同的组织或个人提供的,我们为什…...
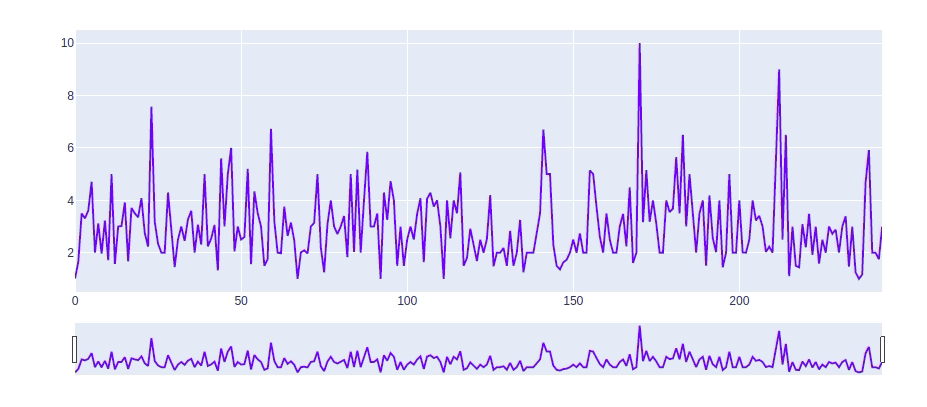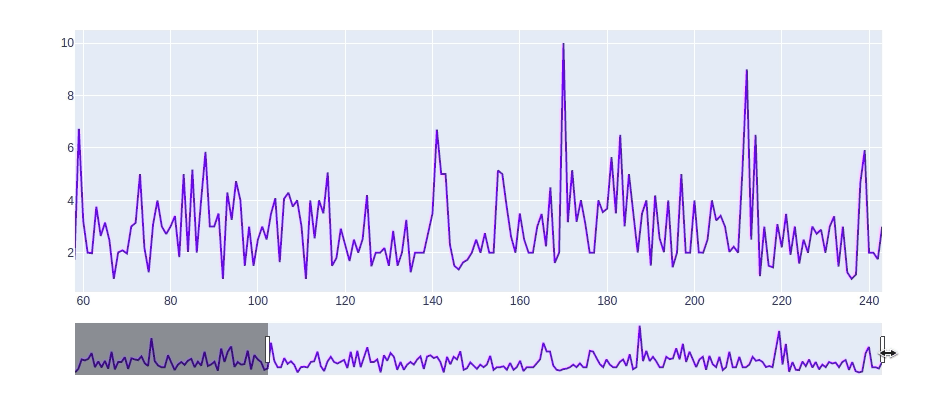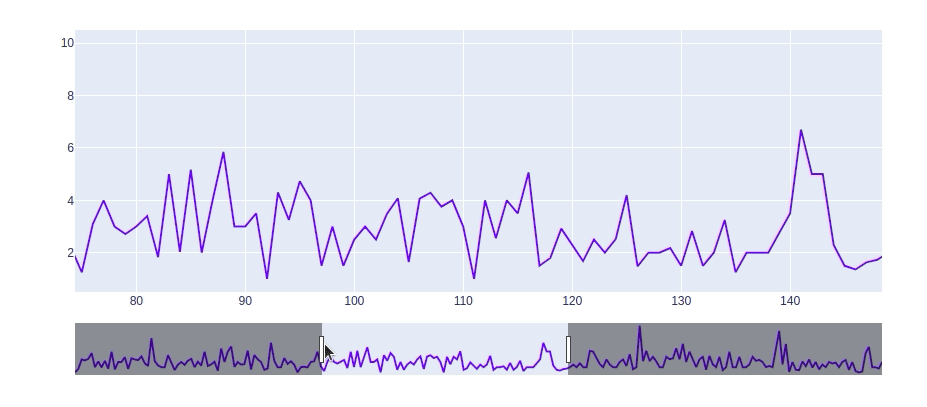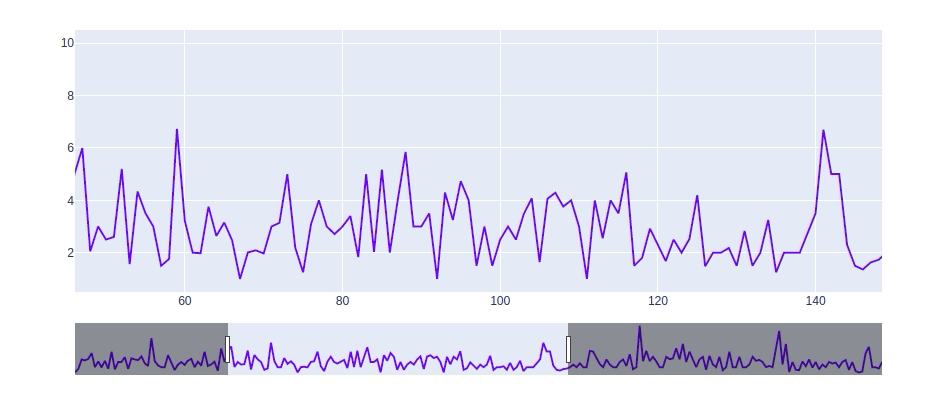
【长文干货】Python可视化教程
文章目录 数据介绍Matplotlib散点图折线图柱形图直方图 Seaborn散点图折线图柱形图直方图 Bokeh散点图折线条形图交互式 Plotly基本组合优化:定制化下拉菜单 总结 数据介绍 在这个小费数据集中,我们记录了20世纪90年代初期餐厅顾客在两个半月内给出的小…...
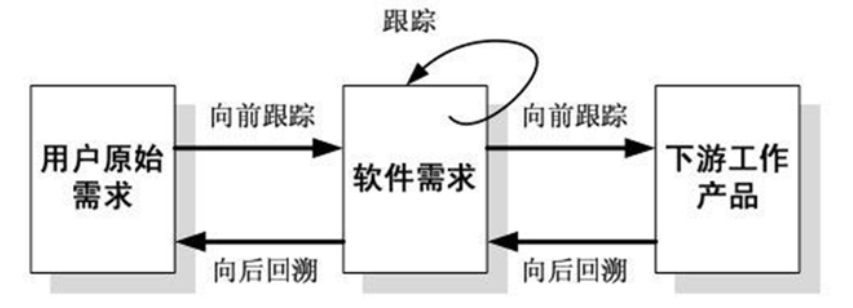
软件工程--需求工程--学习笔记(超详细)
软件需求工程是软件开发周期的第一个阶段,也是关系到软件开发成败最关键阶段,本章讲解需求的基础知识和需求工程的关键活动。这些知识对于结构化方法、面向对象方法、面向服务方法等都是适用的 本文参考教材:沈备军老师的《软件工程原理》 目…...

TemplateHit中提取query和hit比对上序列索引的映射字典
template_hits(Sequence[TemplateHit]数据格式)来自结构数据库搜索结果 python运行hhsearch二进制命令的包装器类 映射索引计算:TemplateHit 中含有 indices_query,需要换算成在原始query序列中的index,hit 中indices_hit 需要减去最小index…...
富必达API:一站式无代码开发集成电商平台、CRM和营销系统
一站式无代码开发的连接解决方案 电子商务、客户服务系统以及其它商业应用,是现代企业运营的重要部分。然而,将这些系统进行有效的整合往往需要复杂的API开发,这对很多企业来说是一个巨大的挑战。富必达API以其一站式的无代码开发解决方案&a…...

聊聊接口最大并发处理数
文章目录 前言并发和并行并发(Concurrency)并行(Parallelism)思考一下 前言 生活在 2023 年的互联网时代下,又是在国内互联网越发内卷的背景下,相信大家面试找工作、网上学习查资料时都了解过互联网系统设…...

6.如何利用LIO-SAM生成可用于机器人/无人机导航的二维/三维栅格地图--以octomap为例
目录 1 octomap的安装 2 二维导航节点的建立及栅格地图的构建 3 三维栅格地图的建立 1 octomap的安装 这里采用命令安装: sudo apt install ros-melodic-octomap-msgs ros-melodic-octomap-ros ros-melodic-octomap-rviz-plugins ros-melodic-octomap-server 这样…...
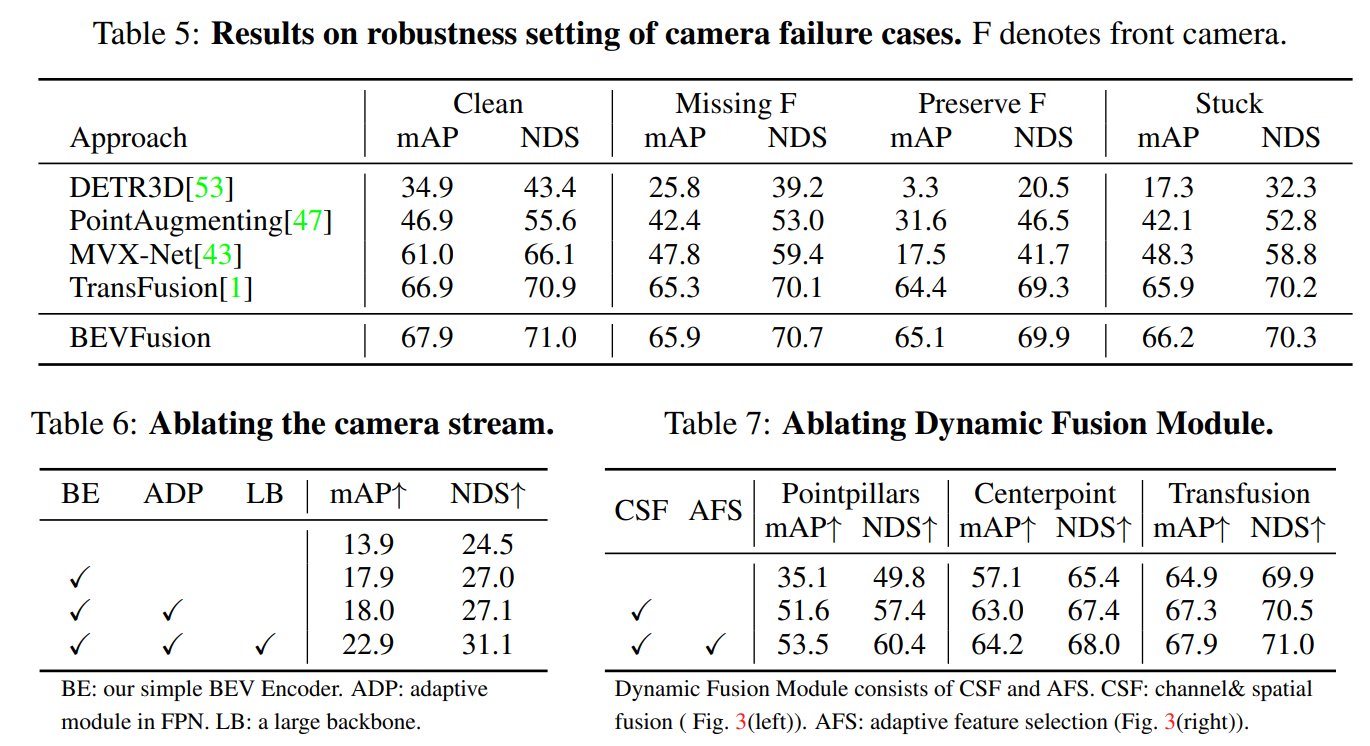
【多传感器融合】BEVFusion: 激光雷达和视觉融合框架 NeurIPS 2022
前言 BEVFusion其实有两篇, 【1】BEVFusion: A Simple and Robust LiDAR-Camera Fusion Framework. NeurIPS 2022 | 北大&阿里提出 【2】BEVFusion: Multi-Task Multi-Sensor Fusion with Unified Bird’s-Eye View Representation 2022 | MIT提出 本文先分…...
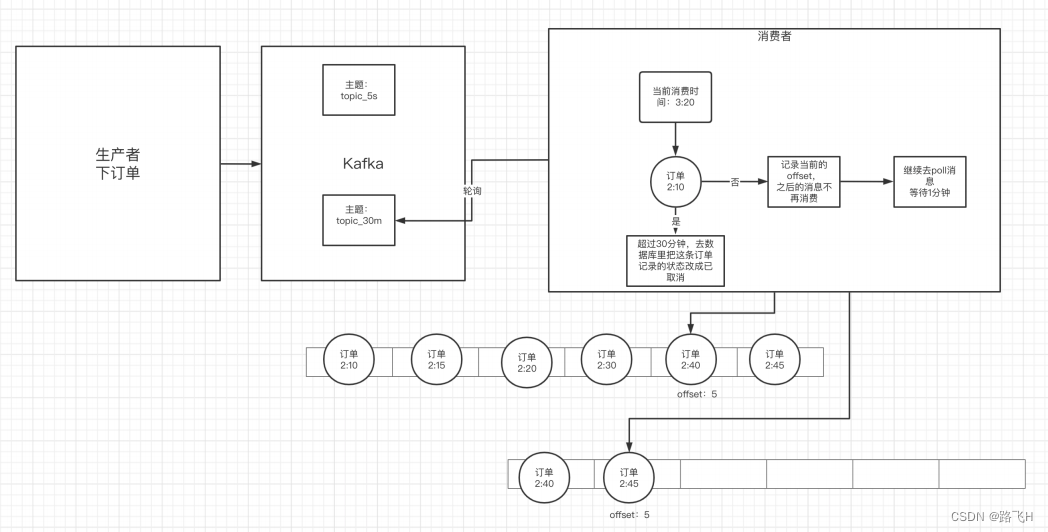
kafka中的常见问题处理
文章目录 1. 如何防⽌消息丢失2. 如何防⽌重复消费3. 如何做到消息的顺序消费4. 如何解决消息积压问题4.1 消息积压问题的出现4.2 消息积压的解决⽅案 5. 实现延时队列的效果5.1 应用场景5.2 具体方案 1. 如何防⽌消息丢失 ⽣产者:1)使⽤同步发送 2&…...
——@Styles装饰器:定义组件重用样式)
HarmonyOS(八)——@Styles装饰器:定义组件重用样式
前言 在前面我们介绍过Builder装饰器和BuilderParam装饰器。今天我们继续介绍另外一个装饰器——Styles装饰器:定义组件重用样式。 如果每个组件的样式都需要单独设置,在开发过程中会出现大量代码在进行重复样式设置,虽然可以复制粘贴&…...

手写VUE后台管理系统5 - 整合状态管理组件pinia
整合状态管理组件 安装整合创建实例挂载使用 pinia 是一个拥有组合式 API 的 Vue 状态管理库。 pinia 官方文档:https://pinia.vuejs.org/zh/introduction.html 安装 yarn add pinia整合 所有与状态相关的文件都放置于项目 src/store 目录下,方便管理 在…...
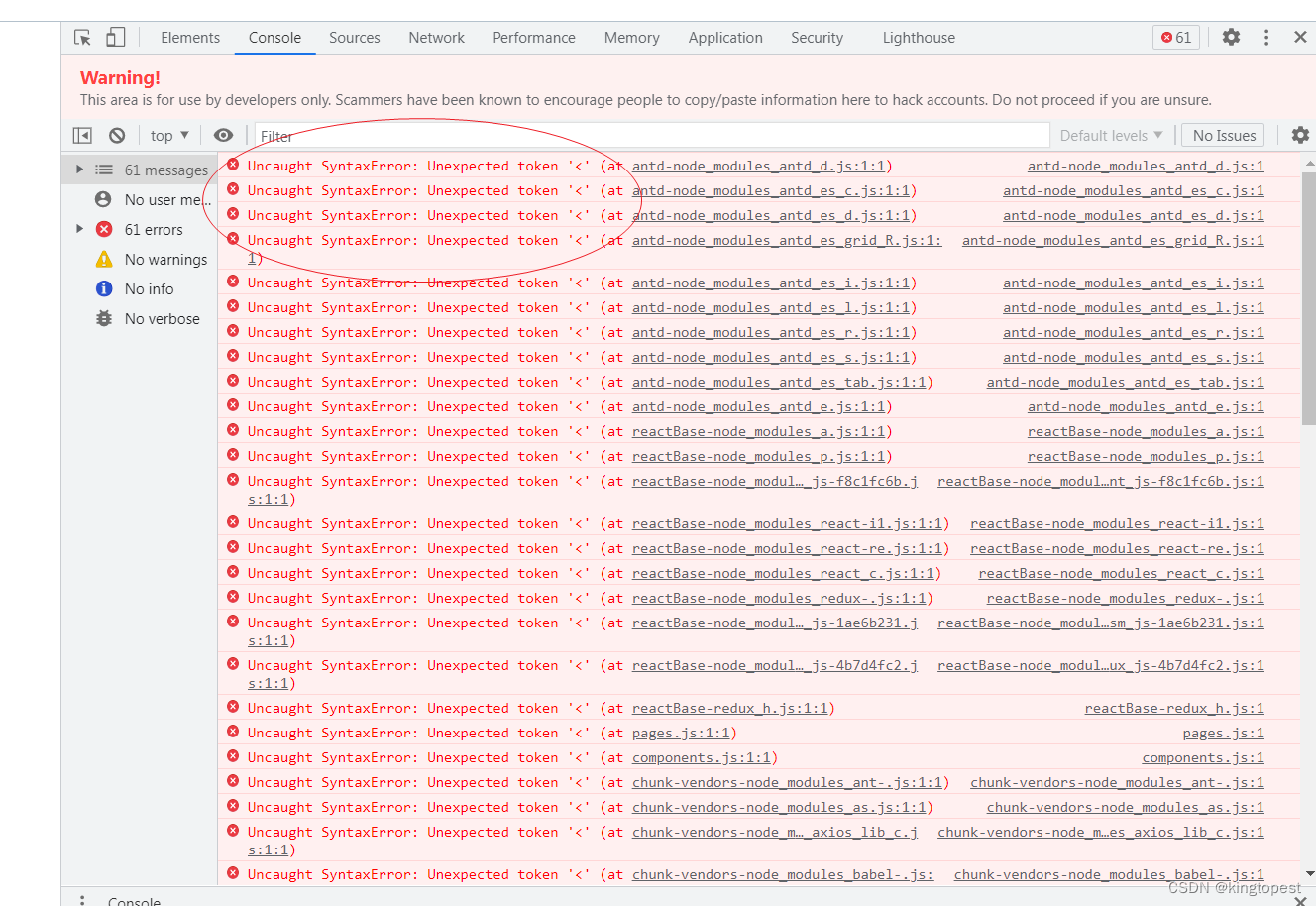
解决webpack打包生成gz格式css/js文件没法在nginx使用的问题--全网唯一正确
本文绝对是全网解决这个问题唯一正确的文章,没有之一! 很多人都说开启nginx gzip压缩,这些人完全是胡说八道!你们到底懂不懂叫gzip压缩啊?! 不信你就试试,如果css/js只有gz文件,ng…...
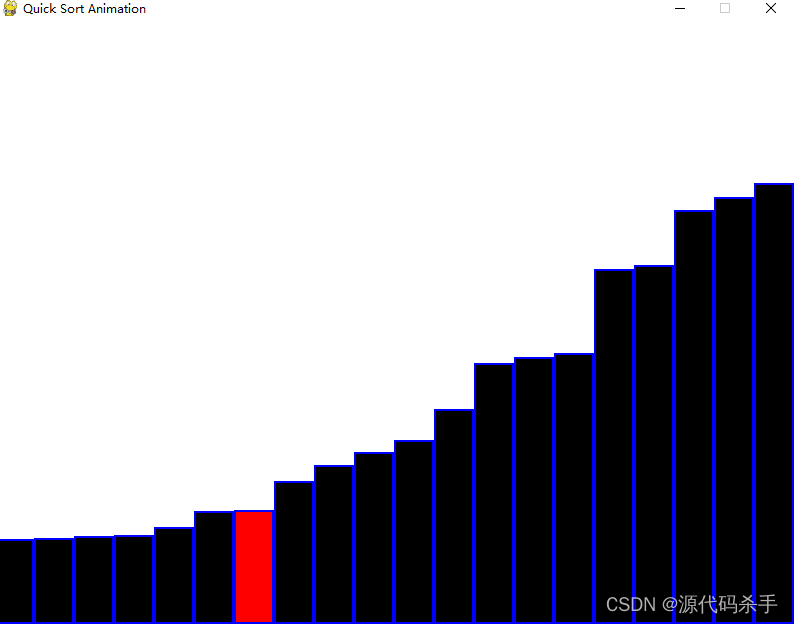
传统算法: Pygame 实现快速排序
使用 Pygame 模块实现了快速排序的动画演示。首先,它生成一个包含随机整数的数组,并通过 Pygame 在屏幕上绘制这个数组的条形图。接着,通过快速排序算法对数组进行排序,动画效果可视化每一步的排序过程。在排序的过程中,程序选择一个基准元素(pivot),将数组分成两部分,…...

HarmonyOS入门开发(三) 持久化存储Preferences
接入鸿蒙几天以来,发现各种和Android不一样的地方,今天来看一下Preferences存储 在Android中比如有ShardPreferences、Mmkv这些持久化存储方式,开发起来很方便,读取速度也很快,在鸿蒙里面也提供了对应的持久化存储方案…...
类和对象——(3)再识对象
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 你说那里有你的梦想,…...
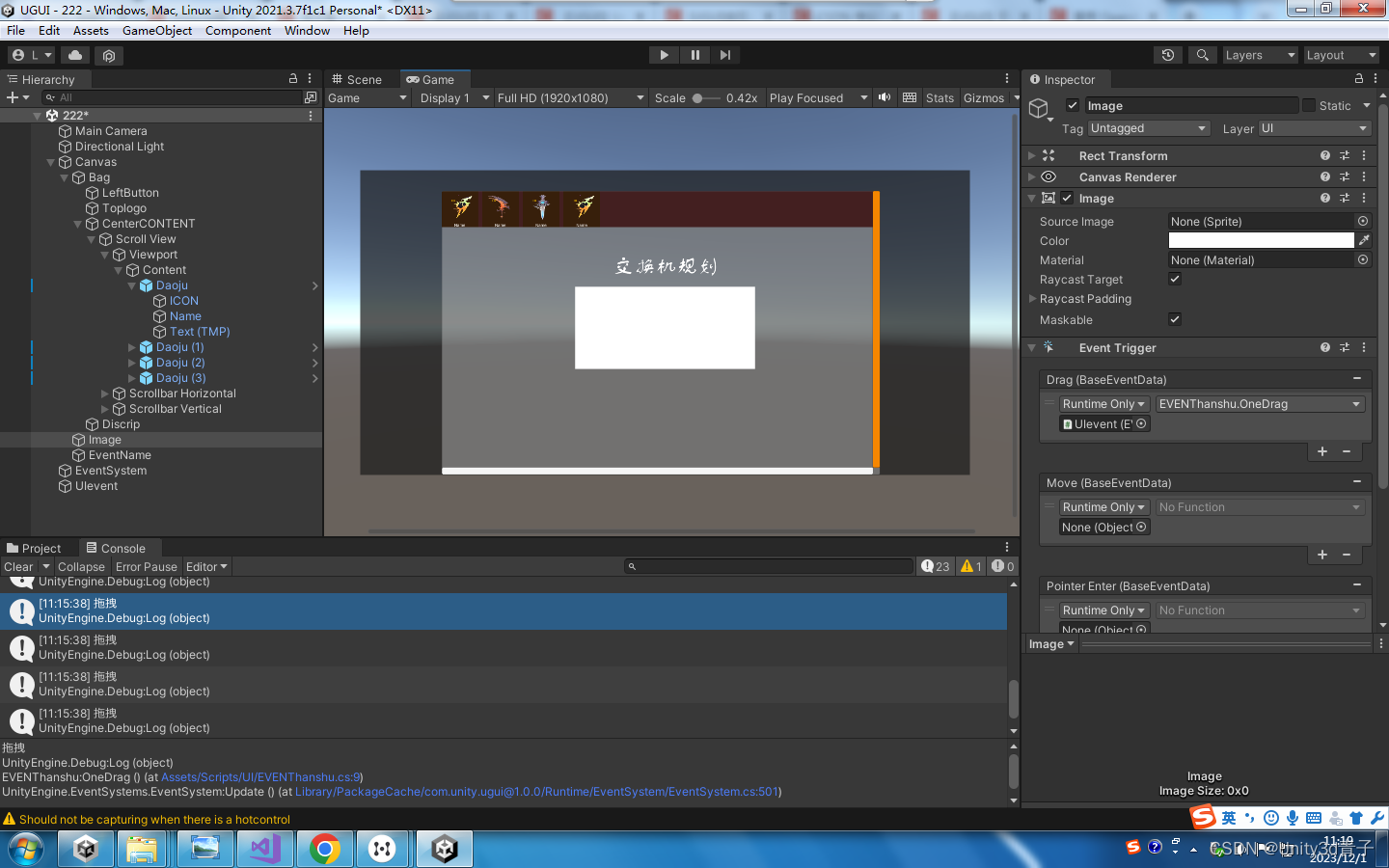
【UGUI】实现背包的常用操作
1. 添加物品 首先,你需要一个包含物品信息的类,比如 InventoryItem: using UnityEngine;[CreateAssetMenu(fileName "NewInventoryItem", menuName "Inventory/Item")] public class InventoryItem : ScriptableObje…...
单机zk安装与zk四字命令
一、下载 Apache ZooKeeper可以在 Linux 系统中使用 wget 命令直接下载,官网地址 Apache ZooKeeper 二、解压 tar -zxvf apache-zookeeper-3.8.3-bin.tar.gz 进去解压的目录中, 进入到 zk 解压目录的 conf 目录,复制 zoo_sample.cfg 文件&a…...

matlab导入excel数据两种常见的方法
在MATLAB中导入Excel数据,你可以使用几种不同的方法。下面是两种常见的方法: 方法一:使用readtable函数 readtable函数允许你导入Excel文件中的数据,并将其存储为表格。 % 指定文件路径 filename C:\your\path\to\file.xlsx;%…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

Linux操作系统共享Windows操作系统的文件
目录 一、共享文件 二、挂载 一、共享文件 点击虚拟机选项-设置 点击选项,设置文件夹共享为总是启用,点击添加,可添加需要共享的文件夹 查询是否共享成功 ls /mnt/hgfs 如果显示Download(这是我共享的文件夹)&…...
