手写VUE后台管理系统5 - 整合状态管理组件pinia
整合状态管理组件
- 安装
- 整合
- 创建实例
- 挂载
- 使用

pinia 是一个拥有组合式 API 的 Vue 状态管理库。
pinia 官方文档:https://pinia.vuejs.org/zh/introduction.html
安装
yarn add pinia
整合
所有与状态相关的文件都放置于项目
src/store目录下,方便管理
在 src 下创建目录 store,目录设计如下:
- index.ts:创建 pinia 实例
- modules:状态管理目录,所以的状态文件统一放置于该目录下
创建实例
创建 index.ts 文件,内容如下
import { createPinia } from 'pinia'const store = createPinia()export default store
挂载
在 main.ts 文件中进行挂载
import { createApp } from 'vue'
import App from './App.vue'
import store from '@/store'const app = createApp(App)
app.use(store)
app.mount('#app')
使用
定义Store
pinia 通过 defineStore 函数进行定义,第一个参数是名称,名称必须保持唯一,第二个参数有两种实现方法:Option 对象及 Setup 函数,接下来将分别介绍这两种方式如何实现定义。
- Option Store
简单的理解:state 用于定义状态对象,getters 相当于 computed 计算属性,actions 相当于方法
import { defineStore } from 'pinia'export const useCounterStore = defineStore('counter', {state: () => ({ count: 0 }),getters: {double: (state) => state.count * 2,},actions: {increment() {this.count++},},
})
- Setup Store
setup 函数更像 vue 的组合式函数,在函数中可以定义响应式属性、方法等,最后返回一个需要暴露出去的属性和方法的对象。
- ref 定义状态对象,对应 Option 模式的 state
- computed 定义计算属性,对应 Option 模式的 getters
- function 定义方法,对应 Option 模式的 actions
import { defineStore } from 'pinia'export const useCounterStore = defineStore('counter', () => {const count = ref(0)function increment() {count.value++}return { count, increment }
})
使用Store
状态对象及计算属性需要使用 storeToRefs 方法进行提取,以保持及响应性,而方法则可以直接调用
const counterStore = useCounterStore()
const { count } = storeToRefs(counterStore)
counterStore.increment()
相关文章:

手写VUE后台管理系统5 - 整合状态管理组件pinia
整合状态管理组件 安装整合创建实例挂载使用 pinia 是一个拥有组合式 API 的 Vue 状态管理库。 pinia 官方文档:https://pinia.vuejs.org/zh/introduction.html 安装 yarn add pinia整合 所有与状态相关的文件都放置于项目 src/store 目录下,方便管理 在…...
解决webpack打包生成gz格式css/js文件没法在nginx使用的问题--全网唯一正确
本文绝对是全网解决这个问题唯一正确的文章,没有之一! 很多人都说开启nginx gzip压缩,这些人完全是胡说八道!你们到底懂不懂叫gzip压缩啊?! 不信你就试试,如果css/js只有gz文件,ng…...
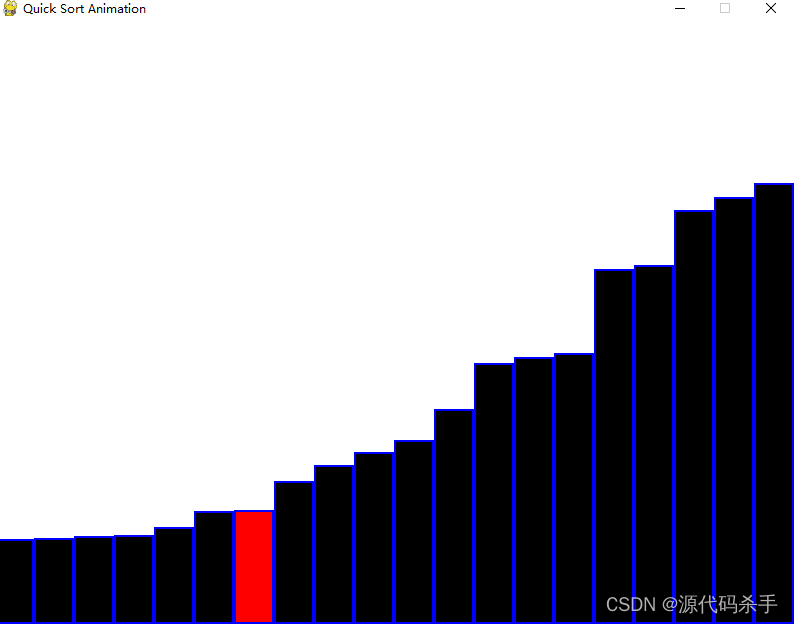
传统算法: Pygame 实现快速排序
使用 Pygame 模块实现了快速排序的动画演示。首先,它生成一个包含随机整数的数组,并通过 Pygame 在屏幕上绘制这个数组的条形图。接着,通过快速排序算法对数组进行排序,动画效果可视化每一步的排序过程。在排序的过程中,程序选择一个基准元素(pivot),将数组分成两部分,…...

HarmonyOS入门开发(三) 持久化存储Preferences
接入鸿蒙几天以来,发现各种和Android不一样的地方,今天来看一下Preferences存储 在Android中比如有ShardPreferences、Mmkv这些持久化存储方式,开发起来很方便,读取速度也很快,在鸿蒙里面也提供了对应的持久化存储方案…...
类和对象——(3)再识对象
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 你说那里有你的梦想,…...
【UGUI】实现背包的常用操作
1. 添加物品 首先,你需要一个包含物品信息的类,比如 InventoryItem: using UnityEngine;[CreateAssetMenu(fileName "NewInventoryItem", menuName "Inventory/Item")] public class InventoryItem : ScriptableObje…...
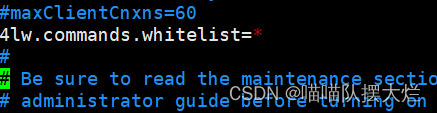
单机zk安装与zk四字命令
一、下载 Apache ZooKeeper可以在 Linux 系统中使用 wget 命令直接下载,官网地址 Apache ZooKeeper 二、解压 tar -zxvf apache-zookeeper-3.8.3-bin.tar.gz 进去解压的目录中, 进入到 zk 解压目录的 conf 目录,复制 zoo_sample.cfg 文件&a…...

matlab导入excel数据两种常见的方法
在MATLAB中导入Excel数据,你可以使用几种不同的方法。下面是两种常见的方法: 方法一:使用readtable函数 readtable函数允许你导入Excel文件中的数据,并将其存储为表格。 % 指定文件路径 filename C:\your\path\to\file.xlsx;%…...
华为全屋智能5.0,无为而“智”
在赖特西塔里埃森混凝土墙的中心壁龛里,一块铜牌上刻着一些英文,意思是“建筑的意义不是屋顶和墙,而是人们生活于其中的空间”。 这句话,取自老子《道德经》中的“凿户牖以为室,当其无,有室之用”。 《理想…...
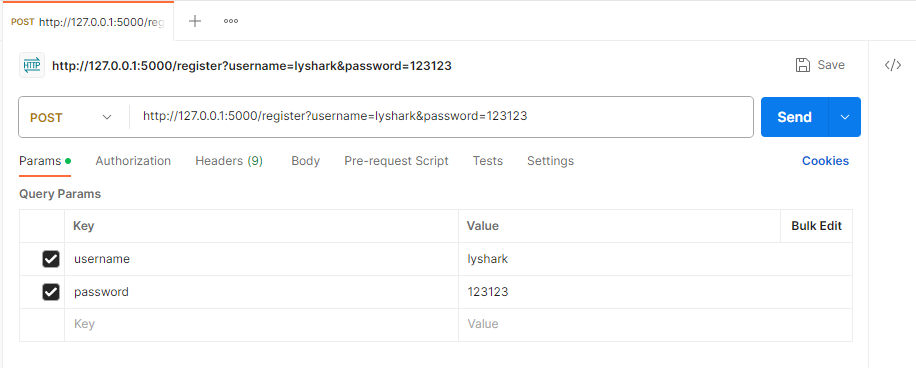
Flask 实现Token认证机制
在Flask框架中,实现Token认证机制并不是一件复杂的事情。除了使用官方提供的flask_httpauth模块或者第三方模块flask-jwt,我们还可以考虑自己实现一个简易版的Token认证工具。自定义Token认证机制的本质是生成一个令牌(Token)&…...
MATLAB 和 Simulink 官方文档下载地址
MATLAB 官方文档中文版下载网址: https://ww2.mathworks.cn/help/pdf_doc/matlab/index.html 如图: MATLAB 官方文档英文版下载网址: https://ww2.mathworks.cn/help/pdf_doc/matlab/index.html?langen 如图: Simulink 官…...

【Element】el-switch开关 点击弹窗确认框时状态先改变----点击弹窗取消框失效
一、背景 需求:在列表中添加定期出账的开关按钮,点击开关时,原来的状态不改变,弹出弹窗;点击弹窗取消按钮:状态不改变,点击弹窗确定按钮:状态改变,并调取列表数据刷新页…...

Java 中最常用的设计模式之一,工厂模式模式的写法,
文章目录 工厂模式1、简单工厂模式2、工厂模式3、抽象工厂4、总结 工厂模式 工厂模式是 Java 中最常用的设计模式之一,工厂模式模式的写法有好几种,这里主要介绍三种:简单工厂模式、工厂模式、抽象工厂模式 1、简单工厂模式 这里以制造cof…...
HTML的学习
知己知彼百战不殆 打算学习一下javascript 所以先从基础的html语言开始 其实就是头部 和身体 头部控制整个 html的语言 title等 <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"width…...

JS设计模式 — 行为委托
回顾一下原型,发现[[Prototype]]机制就是指对象中的一个内部链接引用另一个对象,这个机制的本质就是对象之间的关联关系 1、面相委托的设计 Task {setID: function(ID) { this.id ID; },outputID: function() { console.log( this.id ); } }; // 让 …...

Microsoft Expression Web - 网页布局
在本章中,我们将介绍网页的基本布局。在创建我们的网页布局之前,我们需要考虑我们的内容,然后设计我们希望如何呈现该内容,因为它是在我们的网站上可见的内容。 由我们如何呈现我们的内容,以便我们的观众找到我们的网…...

Java SpringBoot Controller常见写法
文章目录 环境Controller调用脚本运行结果总结 环境 系统: windows 11 工具: java, idea, git bash Controller 接口常见有以下几种方式 其中: Tobj 调用脚本 我的是windows 系统,使用 git bash 窗口运行, 用 cmd 或者 power shell 会有问题 curl …...
-模拟SPI驱动)
【驱动】SPI驱动分析(五)-模拟SPI驱动
简介 模拟SPI驱动是一种软件实现的SPI总线驱动。在没有硬件SPI控制器的系统中,通过软件模拟实现SPI总线的功能。它允许在不修改硬件的情况下,通过GPIO(通用输入/输出)引脚模拟SPI总线的通信,从而与SPI设备进行数据交换…...
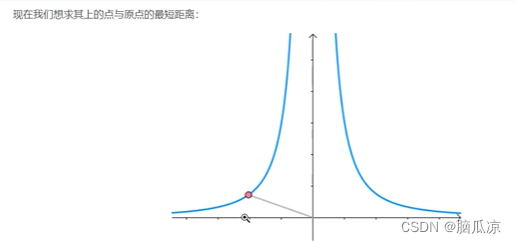
人工智能_机器学习056_拉格朗日乘子法原理推导_公式由来详解_原理详解---人工智能工作笔记0096
https://blog.csdn.net/Soft_Po/article/details/118332454 这里有老师的一篇文章介绍拉格朗日乘子法的原理推导 结合老师的这篇文章我们来看一下详细的推导过程 可以看到上一节我们说,一个有条件的,函数,可以转换为一个,无条件的函数, 根据拉格朗日乘子法,可以创建出一个等…...
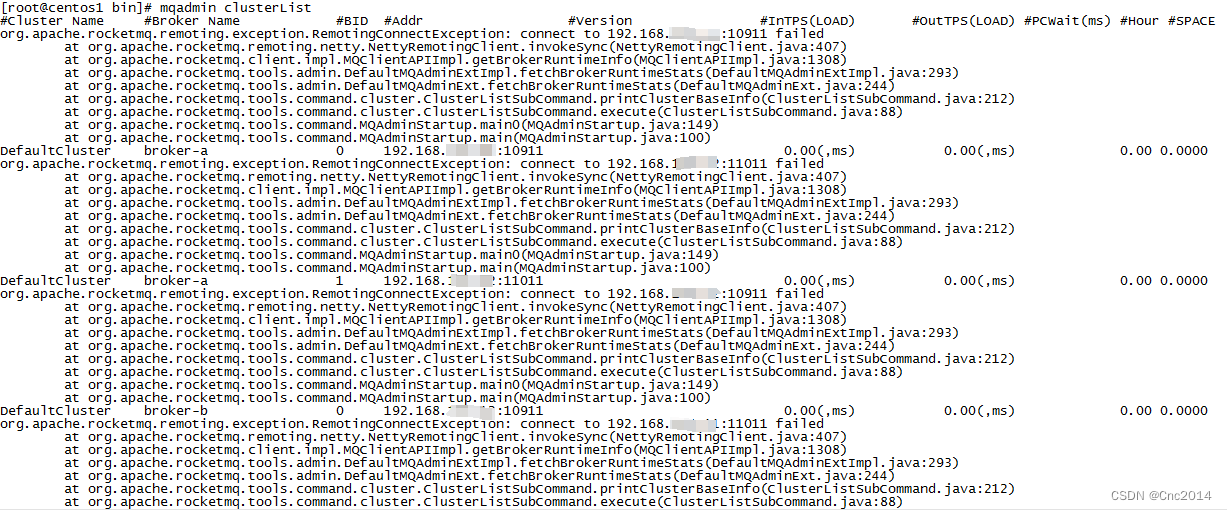
记RocketMQ本地开发环境搭建始末
前言 最近工作中涉及到了RocketMQ的应用,为方便开发决定本地搭建一套RocketMQ的使用环境。 果然实践是个好东西... VMware虚拟环境搭建 这个网上有很多教程,只会比我写的详细有条理,这里就不在赘述了。 虚拟机搭建好之后每次重启电脑都无…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...
