scala可变参数列表使用
在Scala中,可以使用可变参数列表(varargs)来定义一个函数,以接受可变数量的参数。示例如下:
def printArgs(args: String*): Unit = {args.foreach(println)
}// 使用可变参数列表
printArgs("Hello", "World", "Scala")// 也可以传递零个参数
printArgs()
除了支持传入多个参数外,还可以支持传入一个数组转换,如下:
val stringArray: Array[String] = Array("One", "Two", "Three")printArgs(stringArray: _*)_* 语法可以将一个数组的元素作为可变参数传递给函数
相关文章:

scala可变参数列表使用
在Scala中,可以使用可变参数列表(varargs)来定义一个函数,以接受可变数量的参数。示例如下: def printArgs(args: String*): Unit {args.foreach(println) }// 使用可变参数列表 printArgs("Hello", "…...

经验分享:JMeter控制RPS
一、前言 RPS (Request Per Second)一般用来衡量服务端的吞吐量,相比于并发模式,更适合用来摸底服务端的性能。我们可以通过使用 JMeter 的常数吞吐量定时器来限制每个线程的RPS。对于RPS,我们可以把他理解为我们的TPS,我们就…...

JavaScript中的for循环你用对了吗?
🌈个人主页:前端青山 🔥系列专栏:JavaScript篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来JavaScript篇专栏内容:JavaScript-for循环 目录 循环结构 循环思想(三要素) 实现…...
WordPress(10)解决中文连接问题
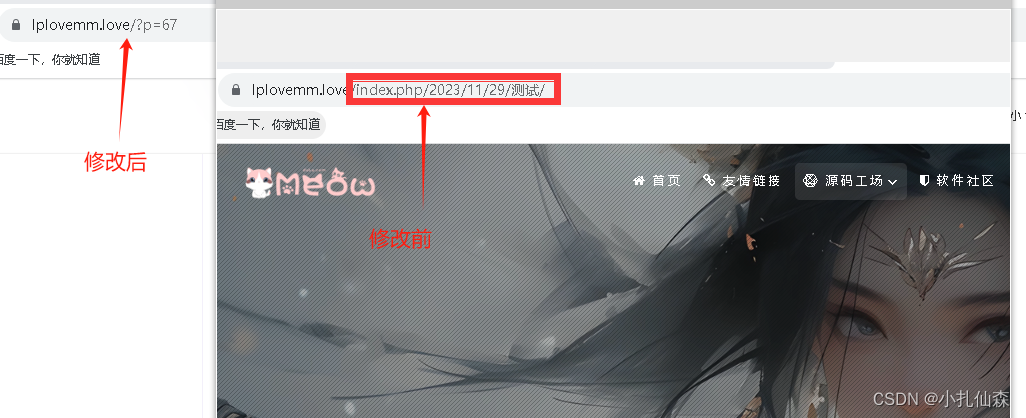
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、修改的前后二、自定义结构讲明三、修改方法前言 提示:这里可以添加本文要记录的大概内容: 1.中文连接如:http://www.lplovemm.love/2023/11/12/测试 2.这种连接在提交sitemap收录的时…...

2023年小美赛认证杯国际赛A题解题思路+数据分享版+部分代码
小美赛作为一个与美赛高度相似的比赛,通常作为很多队伍的美赛练手赛,本次也将尝试帮助大家对A题进行求解,希望能够对大家有所帮助。真实的选题人数评估预计明天进行公布 难度 B>DC>A 选题 A>B>D>C 问题A(MCM&am…...

删除list中除最后一个之外所有的数据
1.你可以新建一个list List<Integer> listnew ArrayList<>();int i0;while (i<100){list.add(i);}List<Integer> subList list.subList(list.size()-1, list.size());System.out.println("原list大小--"list.size());System.out.println("…...
北京筑龙助力中粮集团采购供应链改革加速跑
11月6日,在第六届中国国际进口博览会(简称“进博会”)上,中粮集团与来自全球的供应商签约进口农产品,金额超百亿美元,签约额、进口量、进口来源地覆盖范围均创历史新高。 这只是中粮集团落实集中采购&…...
)
SpringBoot学习笔记-实现微服务:匹配系统(中)
笔记内容转载自 AcWing 的 SpringBoot 框架课讲义,课程链接:AcWing SpringBoot 框架课。 CONTENTS 1. 同步玩家位置1.1 游戏信息的记录1.2 实现多线程同步移动 2. 同步碰撞检测3. 实现游戏结束界面4. 持久化游戏状态4.1 创建数据库表4.2 保存游戏对局信息…...
[Python实现])
【复杂网络建模】——基于代理的社会网络建模(Agent-Based Modeling,ABM)[Python实现]
目录 一、复杂网络建模方法 二、基于代理的社会网络建模实现及Python实现代码 一、复杂网络建模方法 复杂网络是一种由大量相互连接的元素(节点或顶点)组成的网络结构,这些连接通常是非常复杂和动态的。这些网络可以在各种领域中发现,包括社交网络、生物学系统、信息技术…...
)
RSA实现中弱密钥漏洞分析(Analyzing Weak Key Vulnerabilities in RSA Implementation)
点我完整下载:《RSA实现中弱密钥漏洞分析》本科毕业论文一万字.doc RSA实现中弱密钥漏洞分析 "Analyzing Weak Key Vulnerabilities in RSA Implementation" 目录 目录 2 摘要 3 关键词 4 第一章 引言 4 1.1 研究背景 4 1.2 研究目的 5 1.3 研究意义 6 第…...
| 图与网络分析(最大流问题,最小费用最大流问题))
【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析 最大流问题 最大流问题的数学规划模型为: max v f 12 f 13 { f 12 f 13 − f 57 − f 67 0 f 13 f 23 f 34 f 35 . . . 0 ≤ f i j ≤ c i j \max vf_{12}f_{13}\\ \begin{cases} f_{12}f_{13}-f_{57}-f_{67}0 \\ f_{13}f_{23}f_{34}f…...

C语言之结构体详解
C语言之结构体详解 文章目录 C语言之结构体详解1. 结构体类型的声明2. 结构体变量的创建和初始化3. 结构体的特殊声明4. 结构体的自引用结构体的自引用匿名结构体的自引用 5. 结构体内存对齐5.1 练习一5.2 练习三 6. 为什么存在内存对⻬? 1. 结构体类型的声明 struct tag {me…...

学习canvas
Canvas是一个基于像素的渲染引擎,它使用JavaScript API在画布上绘制图像。以下是它的一些优点和缺点: 优点: Canvas的渲染速度快,适合处理大量图像和高度动态的图像。 可以直接操作像素,从而能够创建出高质量、流畅的…...

浏览器的渲染原理
以下内容来源于渡一前端大师课,仅作个人学习记录。 渲染的第一步是 解析HTML 解析过程中遇到CSS解析CSS,遇到JS执行JS。为了提高解析效率,浏览器在开始解析之前,会启动一个预解析的线程,率先下载HTML中的外部CSS文件和…...

从 JSON 转 Java 实体的多种方法详解
将 JSON 数据转换为 Java 对象是现代应用程序开发中常见的任务。在 Java 中,有多种方法可以实现这一目标。本文将详细介绍几种常见的方法,以及它们的优缺点。 1. 手动映射(Manual Mapping) 手动映射是最基础的方法之一ÿ…...
数据库的多表查询(MYSQL)表表联立
根据以上三张表格,对三张表格进行不同的联立,查询并显示符合条件的内容。 1. 查出至少有一个员工的部门。显示部门编号、部门名称、部门位置、部门人数。 mysql> SELECT d.deptno AS 部门编号, d.dname as 部门名称, d.loc as 部门位置, COUNT(e.emp…...
)
P8650 [蓝桥杯 2017 省 A] 正则问题(dfs )
多重括号,利用回溯来对上一层括号中的内容进行反馈 实现: 若为 x 长度加一 若为 ( 进入递归计算 (计算相当于子表达式) 若为 ) 结束当前递归 若为 | …...

【ESP32】手势识别实现笔记:红外温度阵列 | 双三次插值 | 神经网络 | TensorFlow | ESP-DL
目录 一、开发环境搭建与新建工程模板1.1、开发环境搭建与卸载1.2、新建工程目录1.3、自定义组件 二、驱动移植与应用开发2.1、I2C驱动移植与AMG8833应用开发2.2、SPI驱动移植与LCD应用开发2.3、绘制温度云图2.4、启用PSRAM(可选)2.5、画面动静和距离检测…...
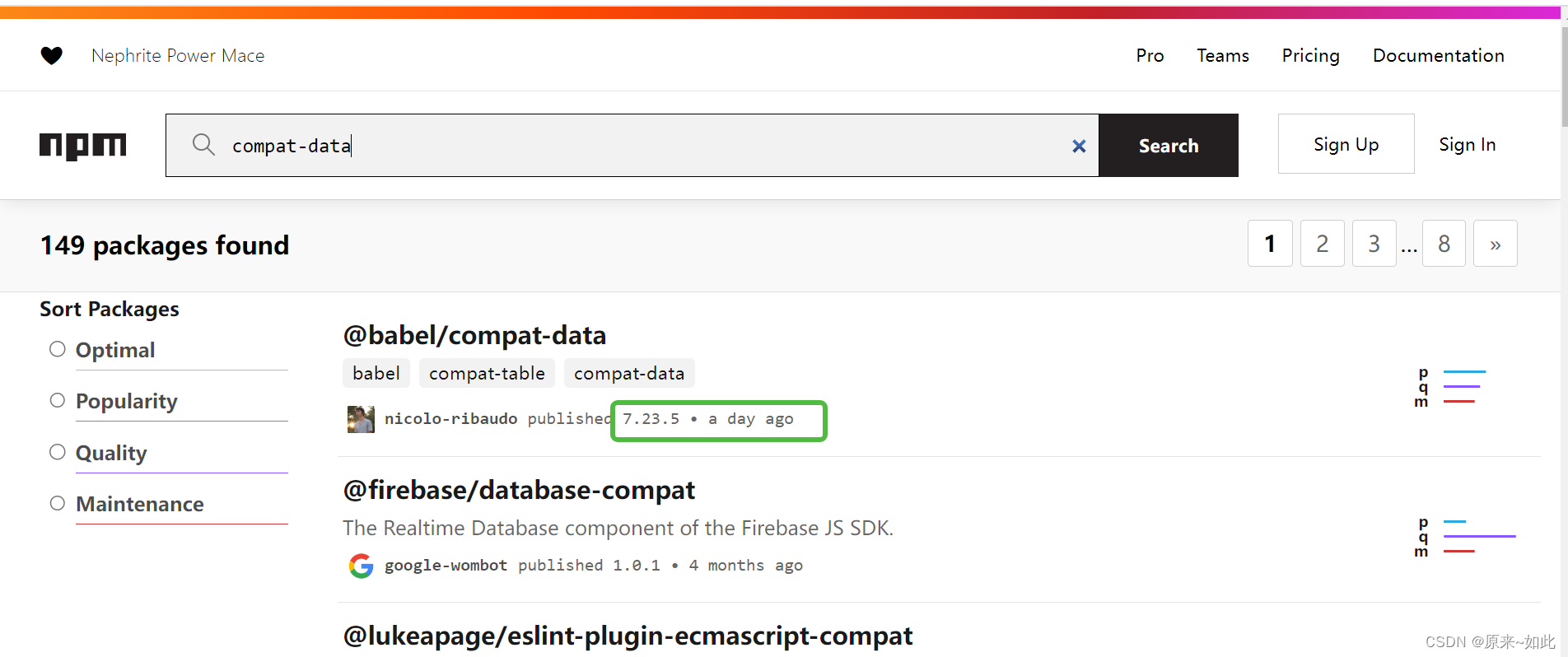
No matching version found for @babel/compat-data@^7.23.5 处理
npm ERR! notarget No matching version found for babel/compat-data^7.23.5 处理 报错信息 npm WARN ERESOLVE overriding peer dependency npm ERR! code ETARGET npm ERR! notarget No matching version found for babel/compat-data^7.23.5. npm ERR! notarget In most …...

手持机|三防智能手机_4寸/5寸/6寸安卓系统三防手机PDA手持终端方案
随着科技的不断发展,三防手持机作为一种多功能设备,正逐渐在各行业得到广泛应用。这款手持机采用高性能处理器,支持高精度北斗定位和工业本安防爆功能,并具备IP67级防水防尘性能和1.5米防跌落能力。因此,它在仓储管理、…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
