【数据结构】二叉排序树(c风格、结合c++引用)
目录
1 基本概念
结构体定义
各种接口
2 二叉排序树的构建和中序遍历
递归版单次插入
非递归版单次插入
3 二叉排序树的查找
非递归版本
递归版本
4 二叉排序树的删除(难点)
1 基本概念
普通二叉排序树是一种简单的数据结构,节点的值根据特定顺序(通常是升序或降序)排列。然而,如果普通二叉排序树不平衡,即左、右子树的高度相差很大时,查询效率可能会降低。因此引出了avl树、红黑树等一系列高阶数据结构。
基本性质:
- 若它的左子树不空,则左子树上所有结点的值均小于它根结点的值。
- 若它的右子树不空,则右子树上所有结点的值均大于它根结点的值。
- 它的左、右子树均为为⼆叉排序树。
- 二叉排序树的查找时间复杂度为树的高度,即为O(以2为底N的对数) ,下面全写成O(logN)
- 二叉排序树的中序遍历输出是一个递增的数列。
结构体定义
typedef struct BSTreeNode
{int val;struct BSTreeNode* left;struct BSTreeNode* right;
}BSTNode,*BiTree;各种接口

关于用到C++中的引用:
BSTNode是结构体struct BSTreeNode的别名,BiTree是结构体struct BSTreeNode指针。
在链表中,首次插入时需要修改头节点,由于头节点的定义也是一个指针,所以要修改一个一级指针,必须传入二级指针或者一级指针的引用,二叉树也是一样,首次插入需要修改根节点的指向,所以这里用引用,当然也可以用二级指针,严蔚敏老师编写的数据结构中也经常用到C++的引用。
而再次或多次进行插入时,我们用cur去遍历链表或二叉树,其实是修改链表和二叉树的一个个结构体,这时我们只需要结构体指针,其实就只需要一级指针即可。
因此,我们直接用二级指针或一级指针的引用,就能解决所有的问题。
2 二叉排序树的构建和中序遍历
构建原则:
①根节点为空,先构建根节点。
②插入节点的值小于根节点的值,去根节点的左子树寻找插入位置。
③插入节点的值大于根节点的值,去根节点的右子树寻找插入位置。
void Create(BiTree& root,int* a,int n)
{for (int i = 0; i < n; ++i){BST_InsertR(root, a[i]);//BST_Insert(root, a[i]);}
}遍历数组O(N),数组每个元素插入O(logN),因此构建的时间复杂度是O(NlogN)。
递归版单次插入
int BST_InsertR(BiTree& root, int x)
{//进行插入if (root == nullptr)//空树或者走到空{BSTNode* newnode = (BiTree)malloc(sizeof(BSTNode));if (newnode == nullptr){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = newnode->right = nullptr;root = newnode;return 1;//插入成功}if (root->val == x)return -1;//插入失败,节点元素值不能相同if (root->val > x)//x小于根节点的值,就去左子树插入return BST_InsertR(root->left, x);if (root->val < x)//x大于于根节点的值,就去右子树插入return BST_InsertR(root->right, x);
}非递归版单次插入
⭕定义两个指针,cur和prev,prev指向cur的根节点,cur最后走到空,对prev的左右指针进行操作,比对prev->val和x,如果val<x,就让prev->right指向新节点,反之。
int BST_Insert(BiTree& root, int x)
{//二叉排序树左孩子的值比根的值要小,右孩子的值比根的值要大BSTNode* newnode = (BiTree)malloc(sizeof(BSTNode));if (newnode == nullptr){perror("malloc fail");exit(-1);}newnode->val = x;newnode->left = newnode->right = nullptr;//第一次进来root为空if (root == nullptr){root = newnode;return 0;}//第二次开始往后遍历BSTNode* cur = root;BSTNode* prev = nullptr;while (cur)//让cur走到空{prev = cur;if (cur->val < x){cur = cur->right;}else if (cur->val > x){cur = cur->left;}else{return -1;//插入失败,不能有元素相等的情况}}if (prev->val < x){prev->right = newnode;}if (prev->val > x){prev->left = newnode;}return 0;//插入成功
}假设我们用这个数组去构建一棵树:
结果是这样的:

中序遍历:
void InOrder(BiTree root)
{if (root == nullptr)//空树或走到空return;InOrder(root->left);//左子树printf("%d ", root->val);//根InOrder(root->right);//右子树
}输出的结果一定是一个递增序列,因此二叉排序树的中序遍历才有意义。
3 二叉排序树的查找
查找原则:
①所查找的值比当前节点的值要小,就去左子树找
②所查找的值比当前节点的值要大,就去右子树找
③查找成功,返回结构体指针BSTNode*/BiTree
二叉排序树的最大查找次数,就是树的深度,类似于折半查找,每查一次排除一半的树。
因此二叉排序树的查找时间复杂度为O(logN) 。
非递归版本
BSTNode* BinarySearch(BiTree root,int x)
{BSTNode* cur = root;while (cur){if (cur->val < x){cur = cur->right;}else if (cur->val > x){cur = cur->left;}else{return cur;}}return nullptr;
}递归版本
BSTNode* BinarySearchR(BiTree root, int x)
{if (root == nullptr)//空树或者找到空了还没找到return nullptr;if (x == root->val)return root;if (x > root->val)//大于就去右子树找return BinarySearchR(root->right, x);if(x < root->val)//小于就去左子树找return BinarySearchR(root->left, x);
}4 二叉排序树的删除(难点)
删除原则:
①删除节点的右子树为空,左子树不为空,把左子树顶上来。
②删除节点的左子树为空,右子树不为空,把右子树顶上来。
③删除节点的左右子树都不为空,要么在左子树中找最大的数据和根的数据交换,要么在右子树中找最小的数据和根的数据交换。
void DeleteNode(BiTree& root, int x)
{if (root == nullptr)//找不到或者根为空,直接返回{return;}//先找后删除,递归if (x < root->val){DeleteNode(root->left, x);}if (x > root->val){DeleteNode(root->right, x);}//找到了,执行删除if (root->val == x){if (root->left == nullptr)//左子树为空,把右子树顶上去{BiTree tmp = root;root = root->right;free(tmp);}else if (root->right == nullptr)//右子树为空,把左子树顶上去{BiTree tmp = root;root = root->left;free(tmp);}else//左右子树均不为空,要么在左子树中找最大的数据和根的数据交换,要么在右子树中找最小的数据和根的数据交换//采用前者即可,左子树的最大数据就是左子树的最右结点{BiTree left = root->left;while (left->right){left = left->right;}root->val = left->val;//free(left);//不能这么做,万一这个结点有左子树怎么办?//只能重新在T的左子树找这个结点,复用递归删除这个结点DeleteNode(root->left, left->val);}}
}图解何为“顶上来”
由于函数传参用到引用,因此root就是上一层函数root->left或者root->right的别名:

定义指针tmp去指向root形参,root形参用root(1)表示一下:
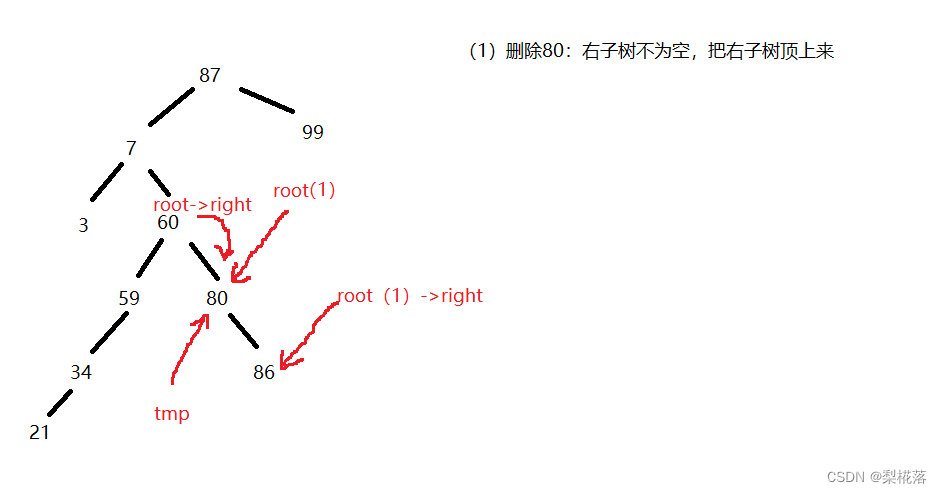
这时我们想让root->right变为root(1)->right,而root(1)就是root->right的别名,因此我们直接让root(1)=root(1)->right,然后去free(tmp),用代码表示就是这样:

同理,右子树为空,把左子树顶上去:

当左右子树都不为空时,要么去左子树中找最大的数据去替换删除节点,要么去右子树中找最小的数据去替换删除节点。
而左子树中的最大数据位于左子树的最右深处节点,右子树中的最小数据位于右子树的最左深处节点。
什么是“替换”:把要删除的根节点的值与左子树最右节点的值交换,然后“删除”掉左子树最右节点;或者把要删除的根节点的值与右子树最左节点的值交换,然后“删除”掉右子树最左节点。

何为删除?真的是直接free掉吗?
 删除59,那它的左子树咋办?直接free就坑了!
删除59,那它的左子树咋办?直接free就坑了!
复用函数去递归删除59,让59的左子树顶上去:
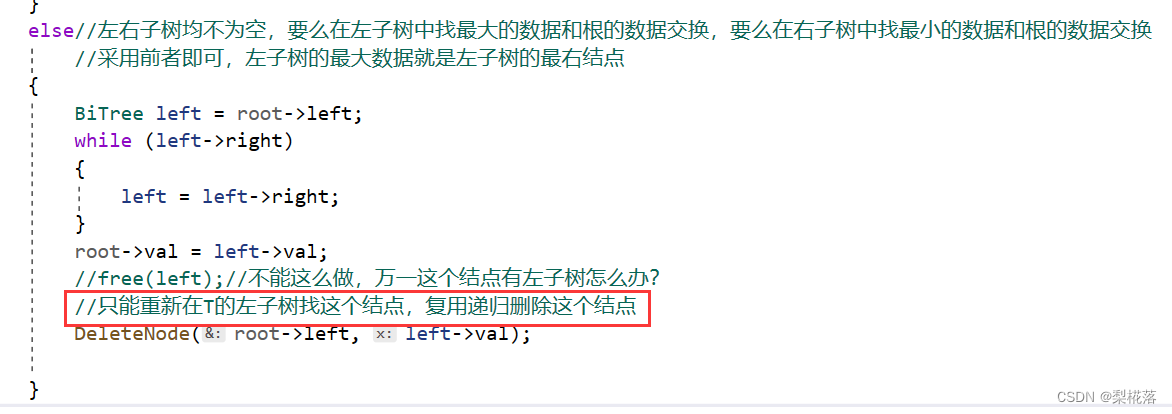
相关文章:

【数据结构】二叉排序树(c风格、结合c++引用)
目录 1 基本概念 结构体定义 各种接口 2 二叉排序树的构建和中序遍历 递归版单次插入 非递归版单次插入 3 二叉排序树的查找 非递归版本 递归版本 4 二叉排序树的删除(难点) 1 基本概念 普通二叉排序树是一种简单的数据结构,节点的值…...
SpringCloudSleuth+Zipkin 整合及关键包汇总
背景 整合了一下 SpringCloudSleuth Zipkin,本来是很简单的东西,但是最终导出依赖包时没注意,导致目标服务始终没有被纳入 Zipkin 的链路追踪中,本文记录这个过程及关键依赖包。 部署zipkin 官网下载最新的 zipkin 可执行包&a…...

腾讯面试笔试题2023.11.30
给定一个由整数组成的非空数组所表示的非负整数如[1,2,3],在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外,这个整数不会以零开头。 (要求只能操作数组,不…...

cesium 融合视频
0 如果是文件,那相当的简单 和untiy 一样,可以添加材质后,将image 直接给材质赋值上,其中abcd 是四个点,这四个点要经过计算 <video id"video" style"display:none" controls loop autoplay&…...
微信小程序踩坑记录
一、引言 作者在开发微信小程序《目的地到了》的过程中遇到过许多问题,这里讲讲一些技术和经验问题。 基本目录机构: 二、问题 1、定位使用 获取定位一定要在app.json里面申明,不然是没办法获取定位信息的 "requiredPrivateInfos"…...

H5 uniapp 接入wx sdk
uniapp因为要兼容小程序等,会重写wx对象,导致引入的jweixin-1.6.0.js中对象不生效。 综合网络资料,有两种解决方案: 一,通过npm工具引入 npm install jweixin-module --save 实际上是借用了wx的另一个对象jWeixin …...

ubuntu离线安装包
方便快捷方式 查看依赖 apt-cache depends 包名(gcc或language-pack-zh-hans)下载deb及其依赖包 # 下载.deb包到指定目录 cd /var/cache/apt/archives apt-get download $(apt-cache depends --recurse --no-recommends --no-suggests --no-conflicts --no-breaks --no-repl…...
电脑如何录音?适合初学者的详细教程
“电脑怎么录音呀?参加了一个学校举办的短视频大赛,视频拍摄都很顺利,音乐却出了问题,朋友说可以用电脑录制一段音乐应付一下,可是我不会操作,有哪位大佬教教我!” 声音是一种强大的媒介&#…...
)
从零开始的C++(二十)
哈希: 用于unorder_map和unorder_set,其本身是一种思想,即通过一个值利用某种算法去映射到另一个值上。利用哈希思想具体实现的是哈希表。 哈希通常函数:插入和查找 1.插入:用某种算法算出插入值对应的插入下标。 …...
shell编程系列(8)-使用sed处理文本
文章目录 引言sed用法详解在文本中定位打印文本替换文本删除文本新增文本 结语 引言 在日常工作学习中我们都会遇到要编辑文本的场景,例如我们要用vim或者nano等命令去编辑代码,处理文本文件等,这些命令的特点都是需要我们进行交互式的实时处…...

NDK是什么?有什么用?需要掌握什么技术栈?
文章目录 NDK使用NDK的优点使用NDK需要掌握的知识C/C的编译原理C/C基本语法和编写能力原生共享库:原生静态库:Java 原生接口 (JNI):应用二进制接口 (ABI): CMakeLLDB参考 NDK NDK(Native Development Kit,…...

《代码长寿经:程序员养生指南》
嘿,代码海洋的航行者们!你们是否有过熬夜加班后,头发渐渐稀疏、眼镜度数直线上升,还不小心多了几斤“编码赘肉”的经历?程序员这个行业,似乎人均亚健康,有人戏称程序员的职业发展路径是…...
)
统计素数并求和(Python)
题目描述 统计素数并求和 本题要求统计给定整数 M M M 和 N N N 区间内素数的个数并对它们求和。 输入格式: 输入在一行中给出两个正整数 M M M 和 N ( 1 ≤ M ≤ N ≤ 500 ) N(1≤M≤N≤500) N(1≤M≤N≤500)。 输出格式: 在一行中顺序输出 M M M 和 N N N 区间内…...
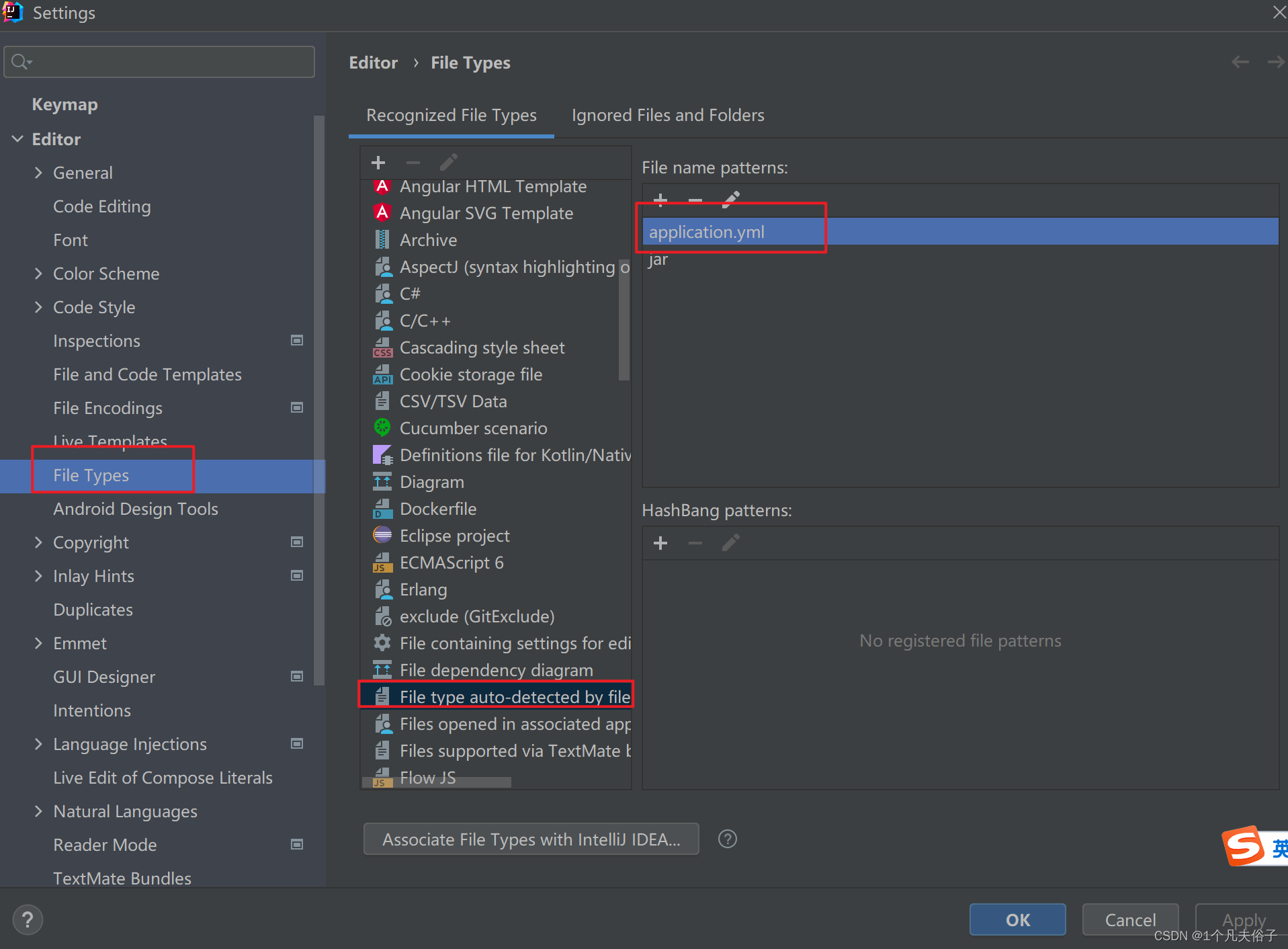
新建的springboot项目中application.xml没有绿色小叶子(不可用)
经常有朋友会遇到新建了一个springboot项目,发现为啥我创建的application.xml配置文件不是绿色的??? 下面教大家如何解决,这也是博主在做测试的时候遇到的: 将当前位置application.xml删掉,重新…...
powershell获取微软o365 21v日志
0x00 背景 o365 21v为o365的大陆版本,主要给国内用户使用。微软提供了powershell工具和接口获取云上日志。微软o365国内的代理目前是世纪互联。本文介绍如何用powershell和配置证书拉取云上日志。 0x01 实践 第一步,ip权限开通: 由世纪互联…...
整体迁移SVN仓库到新的windows服务器
一、背景 公司原有的SVN服务器年代比较久远经常出现重启情况,需要把SVN仓库重新迁移到新的服务器上,在网上也搜到过拷贝Repositories文件直接在新服务器覆盖的迁移方案,但考虑到原有的操作系统和现有的操作系统版本不一致,SVN版本…...

D365 CRM Power Platform 后端开发概览
博主十年前写的后端技术文章大部分都out-of-date啦,有些东西还能在PP系统中继续沿用,大部分东西都变成old fashion了。 博主后续争取多找些时间,将之前的后端开发文档都翻新一遍,争取与时俱进,让它们还能继续使用下个…...

【Java 并发编程】进程线程、lock、设计模式、线程池...
博主:_LJaXi Or 東方幻想郷 专栏: Java | 从入门到入坟 Java 并发编程 并发编程多线程的入门类和接口线程组和线程优先级线程的状态及主要转化方法线程间的通信重排序和 happens-beforevolatilesynchronized 与锁CAS 与原子操作AQS计划任务Stream 并行计…...
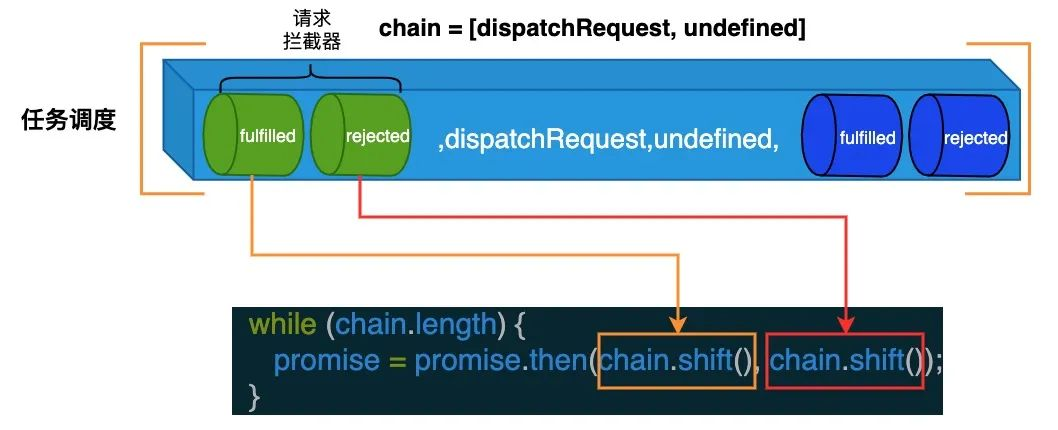
【axios】拦截器:axios.interceptors.request.use|axios.interceptors.response.use
文章目录 概述设置拦截器Axios 拦截器的实现任务注册任务编排任务调度 来源 概述 axios有请求拦截器(request)、响应拦截器(response)、axios自定义回调处理(这里就是我们常用的地方,会将成功和失败的回调…...

webrtc兼容android4.x的一次探索
背景是我们有一个四年前的应用,该应用TargetVersion设定为16,这个应用四年前用了m70版本的webrtc。最近我升级到webrtc-m110,发现各种崩溃,把崩溃修好之后,发现黑屏了。为了处理黑屏,故有本文。 黑屏问题表…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
