深度学习笔记:神经网络权重确定初始值方法
神经网络权重不可为相同的值,比如都为0,因为如果这样网络正向传播输出和反向传播结果对于各权重都完全一样,导致设置多个权重和设一个权重毫无区别。我们需要使用随机数作为网络权重
实验程序
在以下实验中,我们使用5层神经网络,每层神经元个数100,使用sigmoid作为激活函数,向网络传入1000个正态分布随机数,测试使用不同的随机数对网络权重的影响。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):return 1 / (1 + np.exp(-x))def ReLU(x):return np.maximum(0, x)def tanh(x):return np.tanh(x)input_data = np.random.randn(1000, 100) # 1000个数据
node_num = 100 # 各隐藏层的节点(神经元)数
hidden_layer_size = 5 # 隐藏层有5层
activations = {} # 激活值的结果保存在这里x = input_datafor i in range(hidden_layer_size):if i != 0:x = activations[i-1]# 改变初始值进行实验!w = np.random.randn(node_num, node_num) * 1# w = np.random.randn(node_num, node_num) * 0.01# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)a = np.dot(x, w)# 将激活函数的种类也改变,来进行实验!z = sigmoid(a)# z = ReLU(a)# z = tanh(a)activations[i] = z# 绘制直方图
for i, a in activations.items():plt.subplot(1, len(activations), i+1)plt.title(str(i+1) + "-layer")if i != 0: plt.yticks([], [])# plt.xlim(0.1, 1)# plt.ylim(0, 7000)plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
1 标准差为1随机正态

在这一情况下,权重值主要集中于0和1.由于sigmoid在接近0和1时导数趋于0,这一数据分别会导致反向传播中梯度逐渐减小,这一现象称为梯度消失
2 标准差为0.01随机正态

这时神经网络权重集中在0.5附近,此时不会出现梯度消失,但是由于值集中在同一区间,多个神经网络会输出几乎相同的值,使得神经网络表现能力受限(如开头所说)
3 使用Xavier初始值
Xavier初始值为保证各层权重值具有足够广度设计。其推导出的最优初始值为每一层初始权重值是1/√N,其中N为上一层权重个数
使用sigmoid激活函数和Xavier初始值结果:

可以看到此时权重初始值的值域明显大于了之前的取值。Xavier初始值是基于激活函数为线性函数的假设推导出的。sigmoid函数关于(0, 0.5)对称,其在原点附近还不是完美的线性。而tanh函数关于原点对称,在原点附近可以基本近似于直线,其使用Xavier应该会产生更理想的参数值
使用tanh激活函数和Xavier初始值:

ReLU函数的权重设置
ReLU函数有自己独特的默认权重设置,称为He初始值,其公式为2/√N标准差的随机数,N为上一次神经元个数。

在该分布中,各层广度分布基本相同,这使得即使层数加深,也不容易出现梯度消失问题
使用mnist数据集对不同初始化权重方法进行测试:
该程序使用0.01随机正态,Xavier + sigmoid,He + ReLU进行2000轮反向传播,并绘制总损失关于迭代次数图象
# coding: utf-8
import os
import syssys.path.append("D:\AI learning source code") # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],output_size=10, weight_init_std=weight_type)train_loss[key] = []# 2:开始训练==========
for i in range(max_iterations):batch_mask = np.random.choice(train_size, batch_size)x_batch = x_train[batch_mask]t_batch = t_train[batch_mask]for key in weight_init_types.keys():grads = networks[key].gradient(x_batch, t_batch)optimizer.update(networks[key].params, grads)loss = networks[key].loss(x_batch, t_batch)train_loss[key].append(loss)if i % 100 == 0:print("===========" + "iteration:" + str(i) + "===========")for key in weight_init_types.keys():loss = networks[key].loss(x_batch, t_batch)print(key + ":" + str(loss))# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()

在该图象中可以看到,0.01随机正态由于梯度丢失问题,权重更新速率极慢,在2000次迭代中总损失基本没有变化。Xavier和He都正常进行了反向传播得到了更准确的网络参数,其中He似乎学习速率更快一些
相关文章:

深度学习笔记:神经网络权重确定初始值方法
神经网络权重不可为相同的值,比如都为0,因为如果这样网络正向传播输出和反向传播结果对于各权重都完全一样,导致设置多个权重和设一个权重毫无区别。我们需要使用随机数作为网络权重 实验程序 在以下实验中,我们使用5层神经网络…...

关于 python 的异常使用说明 (python 的文件和异常)
文章目录异常1. 处理异常 ZeroDivisionError 异常2. 使用 try-except 代码块3. 使用异常避免崩溃4. else 代码块5. 处理 FileNotFoundError 异常6. 分析文本7. 失败时一声不吭异常 pyhong 使用被异常成为异常的特殊对象来管理程序执行期间发生的错误。 每当发生让 python 不知所…...
Spark RDD持久化
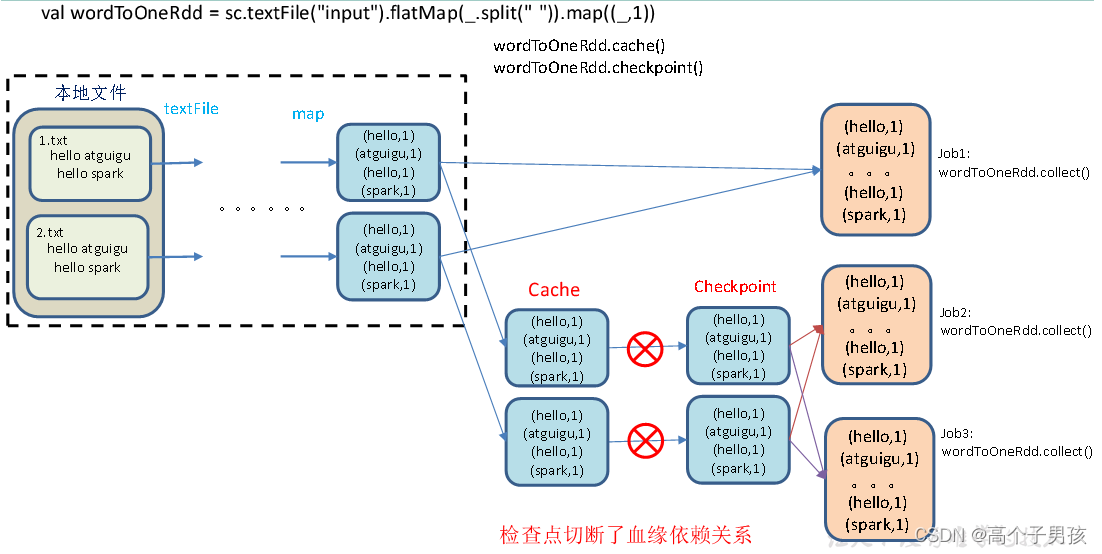
RDD Cache缓存 RDD通过Cache或者Persist方法将前面的计算结果缓存,默认情况下会把数据以序列化的形式缓存在JVM的堆内存中。但是并不是这两个方法被调用时立即缓存,而是触发后面的action时,该RDD将会被缓存在计算节点的内存中,并供…...

【Linux】Linux系统安装Python3和pip3
1.说明 一般来说Linux会自带Python环境,可能是Python3或者Python2,可能有pip也可能没有pip,所以有时候需要自己安装指定的Python版本。Linux系统下的安装方式都大同小异,基本上都是下载安装包然后编译一下,再创建好软…...

用java进行base64加密
首先定义一组密钥,加密和解密使用同一组密钥private final String key "hahahahahaha";也可以随机生成密钥/*** 生成随机密钥* param keySize 密钥大小推荐128 256* return* throws NoSuchAlgorithmException*/public static String generateSecret(int keySize) th…...
torch函数合集
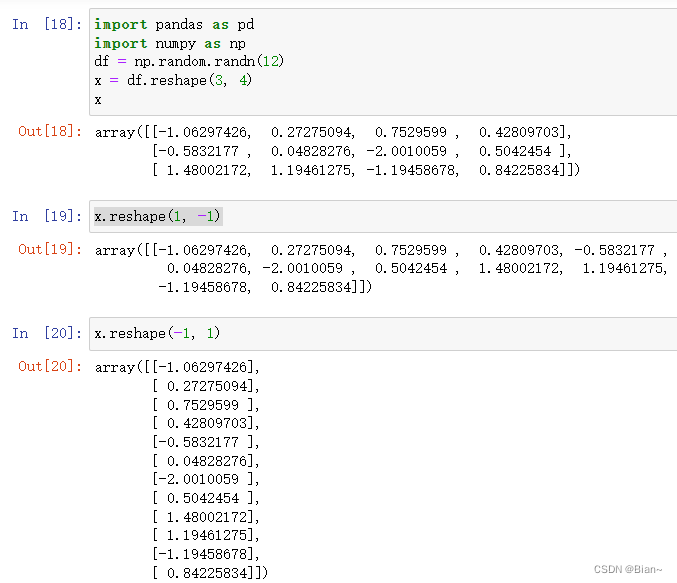
torch.tensor() 原型:torch.tensor(data, dtypeNone, deviceNone, requires_gradFalse) 功能:其中data可以是:list,tuple,NumPy,ndarray等其他类型,torch.tensor会从data中的数据部分做拷贝(而不是直接引用),根据原始数据类型生成相应类型的torch.Tenso…...

AcWing算法提高课-3.1.2信使
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 战争时期,前线有 nnn 个哨所,每个哨所可能会与其他若干个哨所之间有通信联系。 信使负责在哨所之间传递信息,当然,…...

Paddle OCR Win 11下的安装和简单使用教程
Paddle OCR Win 11下的安装和简单使用教程 对于中文的识别,可以考虑直接使用Paddle OCR,识别准确率和部署都相对比较方便。 环境搭建 目前PaddlePaddle 发布到v2.4,先下载paddlepaddle,再下载paddleocr。根据自己设备操作系统进…...

杂谈:数组index问题和对象key问题
面试题一: var arr [1, 2, 3, 4] 问:arr[1] ?; arr[1] ?答:arr[1] 2; arr[1] 2 这里可以再分为两个问题: 1、数组赋值 var arr [1, 2, 3, 4]arr[1] 10; // 数字场景 arr[10] 1; // 字符串场景 arr[a] 1; // 字符串…...
三天Golang快速入门—Slice切片
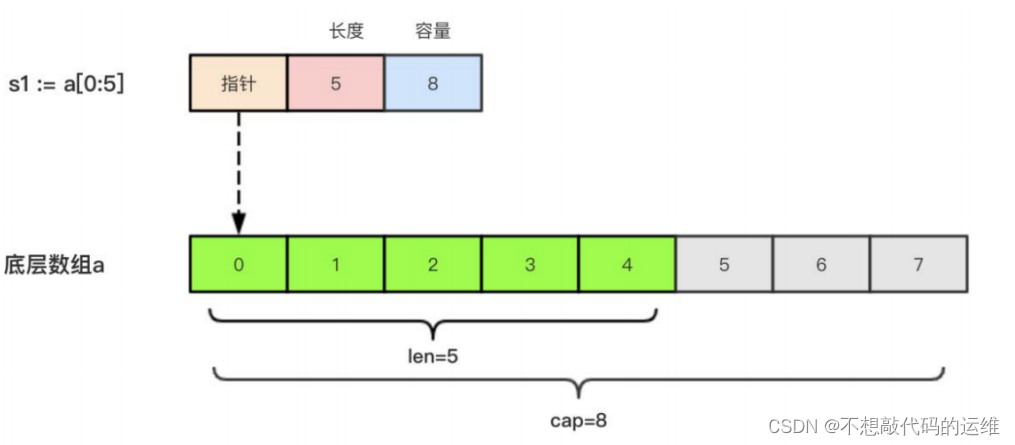
三天Golang快速入门—Slice切片Slice切片切片原理切片遍历append函数操作切片append添加append追加多个切片中删除元素切片合并string和slice的联系Slice切片 切片原理 由三个部分构成,指针、长度、容量指针:指向slice第一个元素对应的数组元素的地址长…...
腾讯会议演示者视图/演讲者视图
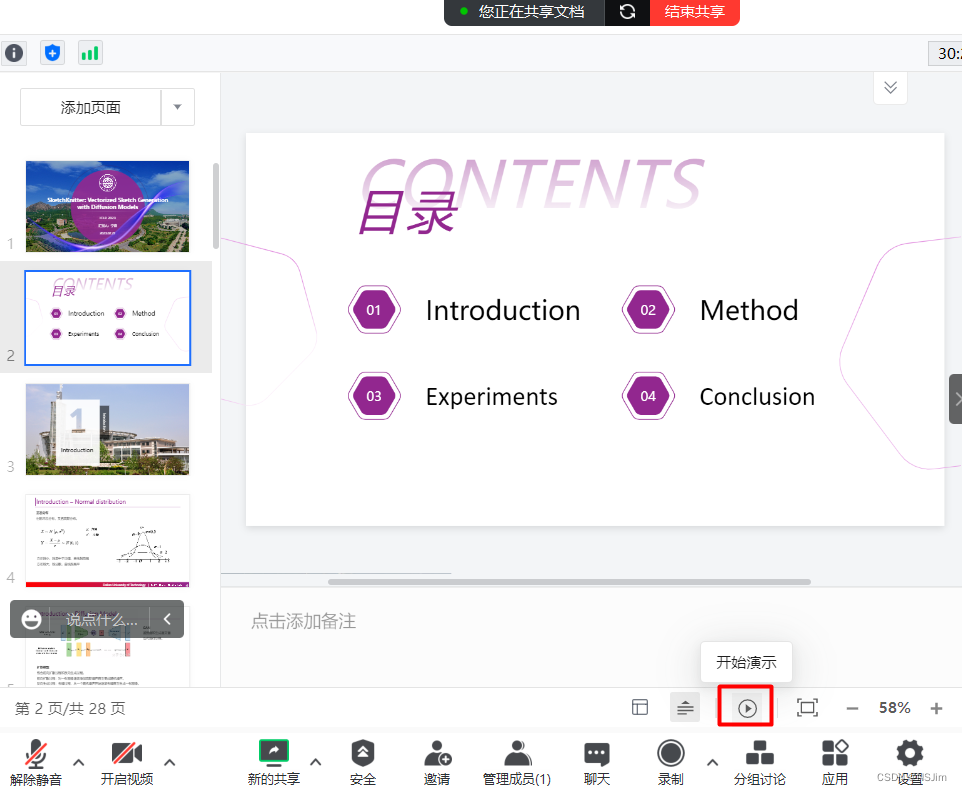
前言 使用腾讯会议共享PPT时,腾讯会议支持共享用户使用演示者视图/演讲者视图,而会议其他成员可以看到正常的放映视图。下面以Win10系统和Office为例,介绍使用步骤。值得一提的是,该方法同时适用于单显示屏和多显示屏。 腾讯会议…...
【C++】类与对象(一)
文章目录1、面向过程和面向对象初步认识2、类的引入3、类的定义4、类的访问限定符5、类的作用域6、类的实例化7、计算类对象的大小8、this指针9、 C语言和C实现Stack的对比1、面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题…...

JavaScript基本语法
本文提到的绝大多数语法都是与Java不同的语法,相同的就不会赘述了.JavaScript的三种引入方式内部js<body><script>alert(hello);</script> </body>行内js<body><div onclick"alert(hello)">这是一个div 点击一下试试</div>…...

OpenCV4.x图像处理实例-道路车辆检测(基于背景消减法)
通过背景消减进行道路车辆检测 文章目录 通过背景消减进行道路车辆检测1、车辆检测思路介绍2、BackgroundSubtractorMOG23、车辆检测实现在本文中,将介绍如何使用简单但有效的背景-前景减法方法执行车辆检测等任务。本文将使用 OpenCV 中使用背景-前景减法和轮廓检测,以及如何…...
pwnlab通关流程
pwnlab通关 关于文件包含,环境变量劫持的一个靶场 信息收集 靶机ip:192.168.112.133 开放端口 根据开放的端口信息决定从80web端口入手 目录信息 在images和upload路径存在目录遍历,config.php被渲染无法查看,upload.php需…...

面向过程与面向对象的区别与联系
目录 什么是面向过程 什么是面向对象 区别 各自的优缺点 什么是面向过程 面向过程是一种以事件为中心的编程思想,编程的时候把解决问题的步骤分析出来,然后用函数把这些步骤实现,在一步一步的具体步骤中再按顺序调用函数。 什么是面向对…...
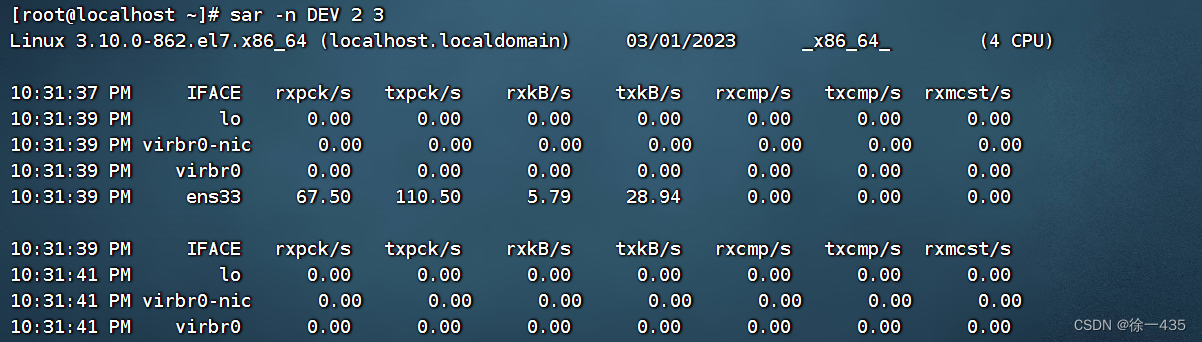
主机状态(查看资源占用情况、查看网络占用情况)
1. 查看资源占用情况 【1】可以通过top命令查看cpu、内存的使用情况,类似windows的任务管理器 默认5s刷新一次 语法:top 可 Ctrl c 退出 2.磁盘信息监控 【1】使用df命令,查看磁盘信息占用情况 语法:df [ -h ] 以更加人性化…...
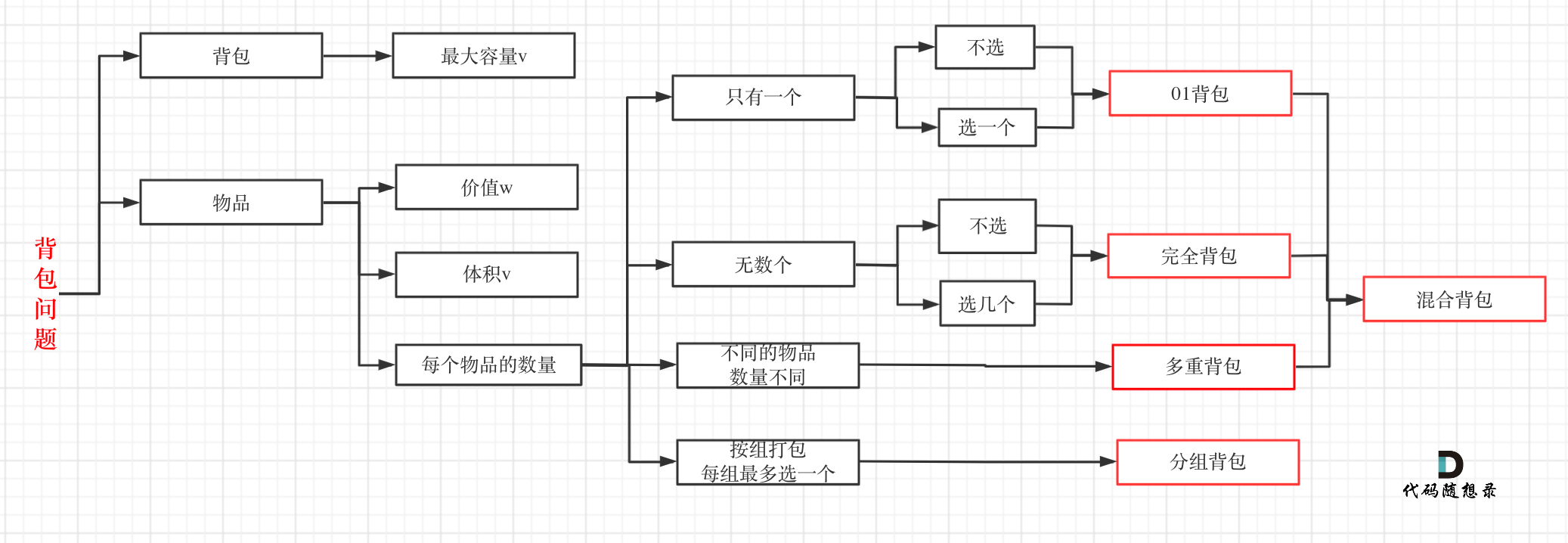
代码随想录算法训练营第四十一天 | 01背包问题-二维数组滚动数组,416. 分割等和子集
一、参考资料01背包问题 二维 https://programmercarl.com/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.html 视频讲解:https://www.bilibili.com/video/BV1cg411g7Y6 01背包问题 一维 https://programmercarl.com/%E8%83%8C%E5…...

VMware NSX 4.1 发布 - 网络安全虚拟化平台
请访问原文链接:VMware NSX 4 - 网络安全虚拟化平台,查看最新版。原创作品,转载请保留出处。 作者主页:www.sysin.org VMware NSX 提供了一个敏捷式软件定义基础架构,用来构建云原生应用程序环境。NSX 专注于为具有异…...

计算理论 复杂度预备知识
文章目录计算理论 复杂度预备知识符号递归表达式求解通项公式主方法Akra-Bazzi 定理计算理论 复杂度预备知识 符号 f(n)o(g(n))f(n)o(g(n))f(n)o(g(n)) :∃c\exists c∃c ,当 nnn 足够大时, f(n)<cg(n)f(n)\lt cg(n)f(n)<cg(n) &#…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...
