【隐私计算】VOLE (Vector Oblivious Linear Evaluation)学习笔记
近年来,VOLE(向量不经意线性评估)被用于构造各种高效安全多方计算协议,具有较低的通信复杂度。最近的CipherGPT则是基于VOLE对线性层进行计算。
1 VOLE总体设计
VOLE的功能如下,VOLE发送 Δ \Delta Δ和 b b b给sender,发送 a a a和 c c c给receiver,并且 c , a , b c, a, b c,a,b满足线性关系: c = Δ ⋅ a + b c=\Delta\cdot a + b c=Δ⋅a+b。

现在主流的VOLE是基于LPN (Learning with Parity Noise)假设/问题来构造的。
2 基于LPN假设的VOLE构造
2.1 前置知识
1 LPN假设
LPN是一个重要的抗量子计算的困难问题。事实上,解决LPN问题等价于解决编码理论中的随机线性码纠错问题(Decoding a random linear code problem)。LPN的表述为:
- 随机生成矩阵 A A A
- 随机生成秘密(行)向量 s s s
- 随机生成错误(行)向量 e e e,满足 H W ( e ) = r ⋅ n HW(e)=r\cdot n HW(e)=r⋅n,其中,参数 r r r是噪声比率
- 计算向量 b = s ⋅ A + e b=s\cdot A+e b=s⋅A+e
则有 ( A , b ) ≈ c ( A ′ , b ′ ) (A, b)\approx _c(A^\prime, b^\prime) (A,b)≈c(A′,b′),其中, ( A ′ , b ′ ) (A^\prime, b^\prime) (A′,b′)是随机生成的。解决LPN问题即使是解决如下问题:给定 A , b A, b A,b,求解 s , e s, e s,e的值。
在密码实践中,为了保证具体的LPN参数设定是困难的,通常选取较大的 k k k,较大的 n n n以及较小的 r r r。
2 函数秘密分享(Functional Secret Sharing, FSS)
FSS它允许计算 P 0 , P 1 P_0, P_1 P0,P1合作计算某个函数 f f f在某个点上的估值 f ( x ) f(x) f(x)。计算完成后, P 0 P_0 P0得到一份share为 f 0 ( x ) f_0(x) f0(x), P 1 P_1 P1得到另一份share为 f 1 ( x ) f_1(x) f1(x),满足 f ( x ) = f 0 ( x ) + f 1 ( x ) f(x)=f_0(x)+f_1(x) f(x)=f0(x)+f1(x),其中, f 0 ( x ) , f 1 ( x ) f_0(x), f_1(x) f0(x),f1(x)是伪随机的。
FSS形式化定义如下:
给定函数 f f f,FSS定义了一对算法 ( G e n , E v a l ) (Gen, Eval) (Gen,Eval):
- F S S . G e n ( 1 λ , f ) FSS.Gen(1^\lambda, f) FSS.Gen(1λ,f):给定安全参数 λ \lambda λ和函数 f f f,生成一对密钥 ( K 0 , K 1 ) (K_0, K_1) (K0,K1)
- F S S . E v a l ( b , K b , x ) FSS.Eval(b, K_b, x) FSS.Eval(b,Kb,x):给定参与方索引 b ∈ { 0 , 1 } b\in \{0, 1\} b∈{0,1},密钥 K b K_b Kb和函数输入 x x x,输出 f b ∈ G f_b\in \mathbb G fb∈G( G \mathbb G G表示群)
由此可见,在FSS过程中,涉及到AES对称加密。
3 VOLE生成器
VOLE定义了两个算法,即 V O L E = ( S e t u p , E x p a n d ) VOLE=(Setup, Expand) VOLE=(Setup,Expand):
- S e t u p ( 1 λ , F , n , x ) Setup(1^\lambda, \mathbb F, n, x) Setup(1λ,F,n,x):输出一对种子 ( s e e d 0 , s e e d 1 ) (seed_0, seed_1) (seed0,seed1),其中, s e e d 1 seed_1 seed1包含输入 x x x
- E x p a n d ( σ , s e e d σ ) Expand(\sigma, seed_\sigma) Expand(σ,seedσ):如 σ = 0 \sigma=0 σ=0,输出 ( u , v ) (u, v) (u,v);如 σ = 1 \sigma=1 σ=1,输出 w w w
于是VOLE满足以下正确性:
( u , v ) ← E x p a n d ( 0 , s e e d 0 ) , w ← E x p a n d ( 1 , s e e d 1 ) (u, v)\leftarrow Expand(0, seed_0), w\leftarrow Expand(1, seed_1) (u,v)←Expand(0,seed0),w←Expand(1,seed1),满足 w = u ⋅ x + v w=u\cdot x+v w=u⋅x+v。
2.2 VOLE的构造方法
现在介绍如何定义Setup和Expand算法,直觉就是在Setup中分配给 P 0 , P 1 P_0, P_1 P0,P1的种子 s e e d 0 , s e e d 1 seed_0, seed_1 seed0,seed1就具有某种线性关系,同时在Expand时仍保持这种线性关系。
尝试1
Setup构造如下:
s e e d 0 ← ( a , b ) ∈ R F k × F k , s e e d 1 ← ( c = a ⋅ x + b , x ) ∈ F k × F seed_0\leftarrow(a, b)\in _R\mathbb F^k\times \mathbb F^k, seed_1\leftarrow (c=a\cdot x+b, x)\in \mathbb F^k\times \mathbb F seed0←(a,b)∈RFk×Fk,seed1←(c=a⋅x+b,x)∈Fk×F
其中 ( a , b ) (a, b) (a,b)是随机生成的,因此 c c c也是随机的。
Expand构造如下:
随机生成一个矩阵 C ∈ F k × n ( k < n ) C\in \mathbb F^{k\times n}(k<n) C∈Fk×n(k<n),并将 C C C作为公开参数发布出去,然后计算:
E x p a n d ( 0 , s e e d 0 ) = ( a ⋅ C , b ⋅ C ) , E x p a n d ( 1 , s e e d 1 ) = c ⋅ C Expand(0, seed_0)=(a\cdot C, b\cdot C), Expand(1, seed_1)=c\cdot C Expand(0,seed0)=(a⋅C,b⋅C),Expand(1,seed1)=c⋅C
由此可见,Expand保持了 a , b , c a, b, c a,b,c的线性关系,并把种子的长度从 k k k扩展到了 n n n。
尝试2
但是上面的构造方式并非伪随机【这里我不是很理解】,借助LPN假设来解决这个问题,Expand构造如下:
E x p a n d ( 0 , s e e d 0 ) = ( a ⋅ C + μ , b ⋅ C − ν b ) , E x p a n d ( 1 , s e e d 1 ) = c ⋅ C + ν c Expand(0, seed_0)=(a\cdot C+\mu, b\cdot C-\nu_b), Expand(1, seed_1)=c\cdot C+\nu_c Expand(0,seed0)=(a⋅C+μ,b⋅C−νb),Expand(1,seed1)=c⋅C+νc
根据LPN可知Expand算法的输出是伪随机的【具体原因?】,但是线性关系难以满足,因为这里 ν c ≠ μ ⋅ x − ν b \nu_c \neq \mu\cdot x-\nu_b νc=μ⋅x−νb,但是如果可以限制 ν c = μ ⋅ x − ν b \nu_c = \mu\cdot x-\nu_b νc=μ⋅x−νb也就是 ν b + ν c = μ ⋅ x \nu_b+\nu_c = \mu\cdot x νb+νc=μ⋅x,线性关系就维持住了。幸运的事,依靠FSS可以生成伪随机 ν b , ν c \nu_b, \nu_c νb,νc满足这个关系。
正式构造
假设LPN假设中公开参数为 F , k , n , t = r n , C ∈ F k × n \mathbb F, k, n, t=rn, C\in \mathbb F^{k\times n} F,k,n,t=rn,C∈Fk×n,则VOLE生成器 G G G可以定义为:
S e t u p ( 1 λ , x ) Setup(1^\lambda, x) Setup(1λ,x):
- 随机生成 ( a , b ) ∈ F k × F k (a, b)\in \mathbb F^k \times \mathbb F^k (a,b)∈Fk×Fk,随机生成 μ ∈ F n \mu\in \mathbb F^n μ∈Fn,满足 H W ( μ ) = t HW(\mu)=t HW(μ)=t
- 计算 c = a ⋅ x + b c=a\cdot x + b c=a⋅x+b
- ( K 0 , K 1 ) ← F S S . G e n ( 1 λ , f ) (K_0, K_1)\leftarrow FSS.Gen(1^\lambda, f) (K0,K1)←FSS.Gen(1λ,f),满足 F S S . E v a l ( 0 , K 0 ) + F S S . E v a l ( 1 , K 1 ) = x ⋅ μ FSS.Eval(0, K_0)+FSS.Eval(1, K_1)=x\cdot \mu FSS.Eval(0,K0)+FSS.Eval(1,K1)=x⋅μ
- s e e d 0 ← ( K 0 , μ , a , b ) , s e e d 1 ← ( K 1 , x , c ) seed_0\leftarrow (K_0, \mu, a, b), seed_1\leftarrow (K_1, x, c) seed0←(K0,μ,a,b),seed1←(K1,x,c)
- 输出 s e e d 0 , s e e d 1 seed_0, seed_1 seed0,seed1
E x p a n d ( σ , s e e d σ ) Expand(\sigma, seed_\sigma) Expand(σ,seedσ):
- 若 σ = 0 \sigma=0 σ=0, s e e d 0 = ( K 0 , μ , a , b ) seed_0=(K_0, \mu, a, b) seed0=(K0,μ,a,b),计算 ν 0 ← F S S . E v a l ( 0 , K 0 ) \nu_0\leftarrow FSS.Eval(0, K_0) ν0←FSS.Eval(0,K0),输出 ( u , v ) ← ( a ⋅ C + μ , b ⋅ C − ν 0 ) (u, v)\leftarrow (a\cdot C+\mu, b\cdot C-\nu_0) (u,v)←(a⋅C+μ,b⋅C−ν0)。即,尝试2中的 E x p a n d ( 0 , s e e d 0 ) = ( a ⋅ C + μ , b ⋅ C − ν 0 ) Expand(0, seed_0)=(a\cdot C+\mu, b\cdot C-\nu_0) Expand(0,seed0)=(a⋅C+μ,b⋅C−ν0)
- 若 σ = 1 \sigma=1 σ=1, s e e d 1 = ( K 1 , x , c ) seed_1=(K_1, x, c) seed1=(K1,x,c),计算 ν 1 ← F S S . E v a l ( 1 , K 1 ) \nu_1\leftarrow FSS.Eval(1, K_1) ν1←FSS.Eval(1,K1),输出 w ← c ⋅ C + ν 1 w\leftarrow c\cdot C+\nu_1 w←c⋅C+ν1。即,尝试2中的 E x p a n d ( 1 , s e e d 1 ) = c ⋅ C + ν 1 Expand(1, seed_1)=c\cdot C+\nu_1 Expand(1,seed1)=c⋅C+ν1
值得注意的是, ν 0 , ν 1 \nu_0, \nu_1 ν0,ν1的生成基于FSS,在Setup中满足 F S S . E v a l ( 0 , K 0 ) + F S S . E v a l ( 1 , K 1 ) = x ⋅ μ FSS.Eval(0, K_0)+FSS.Eval(1, K_1)=x\cdot \mu FSS.Eval(0,K0)+FSS.Eval(1,K1)=x⋅μ,因此很容易得到: ν 0 + ν 1 = x ⋅ μ \nu_0+\nu_1=x\cdot \mu ν0+ν1=x⋅μ,故现在的构造方法符合LPN伪随机性,并且满足线性关系。
3 VOLE在MPC乘法中的应用
在MPC中,安全加法很容易进行,只需在本地做加法即可。而乘法则是困难的,需要双方进行通信实现。
现在考虑乘法 z = x y z=xy z=xy,其中, x x x在 P 0 P_0 P0方, y y y在 P 1 P_1 P1方,双方需要联合计算乘法结果。在算术秘密分享机制下,双方将自己的输入进行拆分,因此计算如下:
x y = ( ⟨ x ⟩ 0 + ⟨ x ⟩ 1 ) ( ⟨ y ⟩ 0 + ⟨ y ⟩ 1 ) = ⟨ x ⟩ 0 ⟨ y ⟩ 0 + ⟨ x ⟩ 1 ⟨ y ⟩ 1 + ⟨ x ⟩ 0 ⟨ y ⟩ 1 + ⟨ x ⟩ 1 ⟨ y ⟩ 0 xy = (\langle x\rangle_0+\langle x\rangle_1)(\langle y\rangle_0+\langle y\rangle_1)=\langle x\rangle_0\langle y\rangle_0+\langle x\rangle_1\langle y\rangle_1+\langle x\rangle_0\langle y\rangle_1+\langle x\rangle_1\langle y\rangle_0 xy=(⟨x⟩0+⟨x⟩1)(⟨y⟩0+⟨y⟩1)=⟨x⟩0⟨y⟩0+⟨x⟩1⟨y⟩1+⟨x⟩0⟨y⟩1+⟨x⟩1⟨y⟩0
其中,前两项均可以在本地计算,而后两项(交叉项,CrossTerm)是MPC计算的重难点。
以 ⟨ x ⟩ 0 ⟨ y ⟩ 1 \langle x\rangle_0\langle y\rangle_1 ⟨x⟩0⟨y⟩1为例,借助VOLE,让 P 0 P_0 P0计算出 v v v【即上面Expand中的 v = b ⋅ C − ν 0 v=b\cdot C-\nu_0 v=b⋅C−ν0】, 让 P 1 P_1 P1计算出 w w w【即上面Expand中的 w = c ⋅ C + ν 1 w=c\cdot C+\nu_1 w=c⋅C+ν1】,满足 ⟨ x ⟩ 0 ⟨ y ⟩ 1 = w − v \langle x\rangle_0\langle y\rangle_1=w-v ⟨x⟩0⟨y⟩1=w−v【 w − v = ν 0 + ν 1 + c ⋅ C − b ⋅ C = u ⋅ x + c ⋅ C − b ⋅ C w-v=\nu_0+\nu_1+c\cdot C-b\cdot C=u\cdot x+c\cdot C-b\cdot C w−v=ν0+ν1+c⋅C−b⋅C=u⋅x+c⋅C−b⋅C,其中 C C C公开, b ⋅ C , c ⋅ C b\cdot C, c\cdot C b⋅C,c⋅C分别在两方计算出来,是明文了,因此 w − v w-v w−v的结果也可算】,即可解决交叉项的计算问题。
4 基于VOLE生成器构造VOLE
VOLE生成器本质是一种伪随机数生成器,生成的两串伪随机数恰好是线性相关的。
预计算生成随机种子
- 可信第三方(TTP)随机生成 r x ∈ F r_x\in \mathbb F rx∈F
- 调用VOLE生成器 G G G,计算 ( s e e d 0 , s e e d 1 ) ← S e t u p ( 1 λ , r ) (seed_0, seed_1)\leftarrow Setup(1^\lambda, r) (seed0,seed1)←Setup(1λ,r)
- 将 s e e d 0 seed_0 seed0发给 P 0 P_0 P0,将 ( r x , s e e d 1 ) (r_x, seed_1) (rx,seed1)发给 P 1 P_1 P1
预计算生成 ( r u , r v , r w ) (r_u, r_v, r_w) (ru,rv,rw)
- P 0 P_0 P0计算 ( r u , r v ) ← E x p a n d ( 0 , s e e d 0 ) (r_u, r_v)\leftarrow Expand(0, seed_0) (ru,rv)←Expand(0,seed0)
- P 1 P_1 P1计算 r w ← E x p a n d ( 1 , s e e d 1 ) r_w\leftarrow Expand(1, seed_1) rw←Expand(1,seed1)
在线计算
现在 P 0 P_0 P0拥有 ( u , v ) (u, v) (u,v), P 1 P_1 P1拥有 x x x【于是,我们又回到了最开头那幅图】

- P 1 P_1 P1计算 m x ← x − r x m_x\leftarrow x-r_x mx←x−rx,并将 m x m_x mx发给 P 0 P_0 P0
- P 0 P_0 P0计算 m u ← u − r u , m v ← m x r u + v − r v m_u\leftarrow u-r_u, m_v\leftarrow m_xr_u+v-r_v mu←u−ru,mv←mxru+v−rv,并发给 P 1 P_1 P1
- P 1 P_1 P1计算 w ← m u x + m v + r w w\leftarrow m_ux+m_v+r_w w←mux+mv+rw
正确性
预计算阶段得到的随机向量满足 r w = r u ⋅ r x + r v r_w=r_u\cdot r_x+r_v rw=ru⋅rx+rv,于是 P 1 P_1 P1方:
w = m u x + m v + r w = ( u − r u ) x + ( m x r u + v − r v ) + ( r u ⋅ r x + r v ) = ( u − r u ) x + ( ( x − r x ) r u + v − r v ) + ( r u ⋅ r x + r v ) = u x − r u x + r u x − r u r x + v − r v + r u r x + r v = u x + v w=m_ux+m_v+r_w\\~~~~=(u-r_u)x+(m_xr_u+v-r_v)+(r_u\cdot r_x+r_v)\\~~~~=(u-r_u)x+((x-r_x)r_u+v-r_v)+(r_u\cdot r_x+r_v)\\~~~~=ux-r_ux+r_ux-r_ur_x+v-r_v+r_ur_x+r_v\\~~~~=ux+v w=mux+mv+rw =(u−ru)x+(mxru+v−rv)+(ru⋅rx+rv) =(u−ru)x+((x−rx)ru+v−rv)+(ru⋅rx+rv) =ux−rux+rux−rurx+v−rv+rurx+rv =ux+v
这个形式和图中的 c = Δ ⋅ a + b c=\Delta\cdot a+b c=Δ⋅a+b完全一致。由此可见,至此我们已经成功构造出VOLE的线性表达式。
CipherGPT中的乘法计算【简化清晰版】
假设Client拥有 x x x,Server拥有 y y y,现在要计算 z = x y z=xy z=xy(为了更清晰的表达,这里的推导暂不区分矩阵和向量,重在梳理算法流程)。
此时 y y y是Server端模型参数,因此推理时提前已知,于是可以通过VOLE生成器在预处理阶段构造VOLE关系: w = u ⋅ y + v w = u\cdot y+v w=u⋅y+v,其中,Client拥有 ( u , v ) (u, v) (u,v),Server拥有 ( y , w ) (y, w) (y,w)。
那么重点来了,如何在在线阶段实现 z = x y z=xy z=xy的计算?
- Client计算 x s = x − u x_s=x-u xs=x−u,并将 x s x_s xs发送给Server
- Server计算 x s ⋅ y = ( x − u ) ⋅ y = x ⋅ y − u ⋅ y x_s\cdot y=(x-u)\cdot y=x\cdot y-u\cdot y xs⋅y=(x−u)⋅y=x⋅y−u⋅y
- 于是,我们知道 x ⋅ y = ( x s + u ) ⋅ y = x s ⋅ y + u ⋅ y = x s ⋅ y + w − v x\cdot y=(x_s+u)\cdot y=x_s\cdot y+u\cdot y=x_s\cdot y+w-v x⋅y=(xs+u)⋅y=xs⋅y+u⋅y=xs⋅y+w−v
- 很容易发现,将 x s ⋅ y + w x_s\cdot y+w xs⋅y+w分配给Server,将 − v -v −v分配给Client,即可实现乘法计算
参考资料
基于LPN假设构造VOLE
相关文章:

【隐私计算】VOLE (Vector Oblivious Linear Evaluation)学习笔记
近年来,VOLE(向量不经意线性评估)被用于构造各种高效安全多方计算协议,具有较低的通信复杂度。最近的CipherGPT则是基于VOLE对线性层进行计算。 1 VOLE总体设计 VOLE的功能如下,VOLE发送 Δ \Delta Δ和 b b b给send…...
国产linux单用户模式破解无密码登陆 (麒麟系统用户登录密码遗忘解决办法)
笔者手里有一批国产linu系统,目前开始用在日常的工作生产环境中,我这个老程序猿勉为其难的充当运维的或网管的角色。 国产linux系统常见的为麒麟Linux,统信UOS等,基本都是基于debian再开发的linux。 问题描述: 因为…...

GPT市场将取代插件商店 openAI已经关闭plugins申请,全部集成到GPTs(Actions)来连接现实世界,可以与物理世界互动了。
Actions使用了plugins的许多核心思想,也增加了新的特性。 ChatGPT的"Actions"与"Plugins"是OpenAI在GPT模型中引入的两种不同的功能扩展机制。这两种机制的目的是增强模型的功能,使其能够处理更多样化的任务和请求。下面是对两者的比…...

PHP定义的变量 常量 静态变量等储存在内存什么位置?
在 PHP 中,变量、常量和静态变量都存储在内存中。它们的存储位置和生命周期有所不同。 变量:PHP 中的变量是动态类型的,它们的值和类型可以随时改变。当 PHP 脚本执行时,会在内存中分配一块空间来存储变量的值,这个空…...
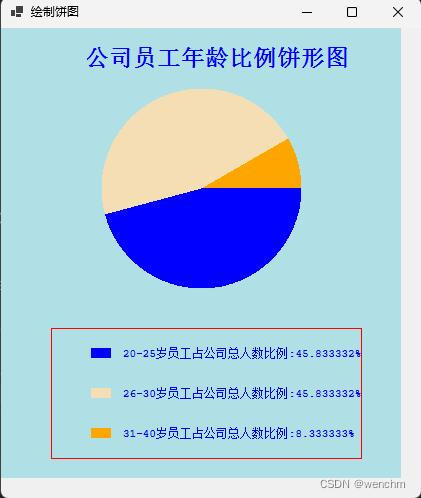
C#中GDI+绘图应用(柱形图、折线图和饼形图)
目录 一、柱形图 1.示例源码 2.生成效果 二、折线图 1.示例源码 2.生成效果 三、饼形图 1.示例源码 2.生成效果 GDI绘制的一些常用的图形,其中包括柱形图、折线图和饼形图。 一、柱形图 柱形图也称为条形图,是程序开发中比较常用的一种图表技术…...

连锁零售企业如何提高异地组网的稳定性?
随着数字化时代的到来,连锁零售企业面临着日益复杂和多样化的网络挑战。连锁零售企业是在不同地理位置拥有分支机构和零售店,可能同城或异地,需要确保各个地点之间的网络连接稳定和可靠。但由于不同地区的网络基础设施差异、网络延迟和带宽限…...

如何靠掌握自己的大数据打破信息流的壁垒?
在当今数字化时代,打造自己的私域流量已经成为商家乃至获取竞争优势的关键手段之一。通过掌握自己的大数据,可以更好地了解用户需求和市场趋势,优化产品和服务,从而打破信息流的壁垒。本文将就如何通过打造自己的私域流量并掌握大…...
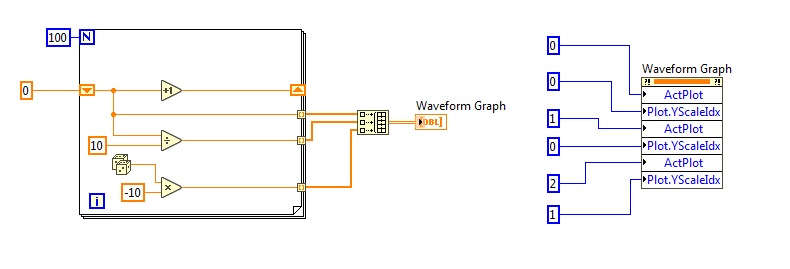
LabVIEW绘制带有多个不同标尺的波形图
LabVIEW绘制带有多个不同标尺的波形图 通过在同一波形图上使用多个轴,可以使用不同的标尺绘制数据。请按照以下步骤操作。 将波形图或图表控件放在前面板上。 1. 右键点击您要创建多个标尺的轴,然后选择复制标尺。例如,如果要为一个…...

Oracle行转列,列转行使用实例
-----1.行转换为列 select a.fworkcenter as 车间,F1||-数量 as 类型, fspec as 规格 ,ftype as 前缀 , to_char(fdate,YYYY-MM-dd) as 日期, (case when a.fcode in (900,901) then to_char(fcount,fm90.990) else cast(fcount as varchar(20)) end) 值 , …...

056-第三代软件开发-软件打包
第三代软件开发-软件打包 文章目录 第三代软件开发-软件打包项目介绍软件打包1 下载 linuxdepoyqt 工具2 安装 linuxdepoyqt3 qmake配置4 打包程序 总结 关键字: Qt、 Qml、 linuxdeployqt、 Ubuntu、 AppImage 项目介绍 欢迎来到我们的 QML & C 项目&…...

C++相关闲碎记录(2)
1、误用shared_ptr int* p new int; shared_ptr<int> sp1(p); shared_ptr<int> sp2(p); //error // 通过原始指针两次创建shared_ptr是错误的shared_ptr<int> sp1(new int); shared_ptr<int> sp2(sp1); //ok 如果对C相关闲碎记录(1)中记录的shar…...

如何快速搭建一个大模型?简单的UI实现
🔥博客主页:真的睡不醒 🚀系列专栏:深度学习环境搭建、环境配置问题解决、自然语言处理、语音信号处理、项目开发 💘每日语录:相信自己,一路风景一路歌,人生之美,正在于…...

国家开放大学 平时作业 测试题 训练
试卷代号:1340 古代小说戏曲专题 参考试题(开卷) 一、选择(每题1分,共10分) 1.下列作品中属于唐传奇的是( )。 A.《公孙九娘》 B.《观音作别》 C《碾玉观音》 …...
)
后端防止重复提交相同数据处理方式(Redis)
使用AOP注解处理接口幂等性,默认禁止同一用户在上次提交未果后10秒内又重复提交 在原先的sameUrlData的注解上进行了copy新建优化,使用redis去setnx的参数视项目使用点而调整,不一定是每个项目都适合这种取参形式。 源码如下: package com…...

最小栈[中等]
优质博文:IT-BLOG-CN 一、题目 设计一个支持push,pop,top操作,并能在常数时间内检索到最小元素的栈。 实现MinStack类: MinStack()初始化堆栈对象。 void push(int val)将元素val推入堆栈。 void pop()删除堆栈顶部的元素。 in…...
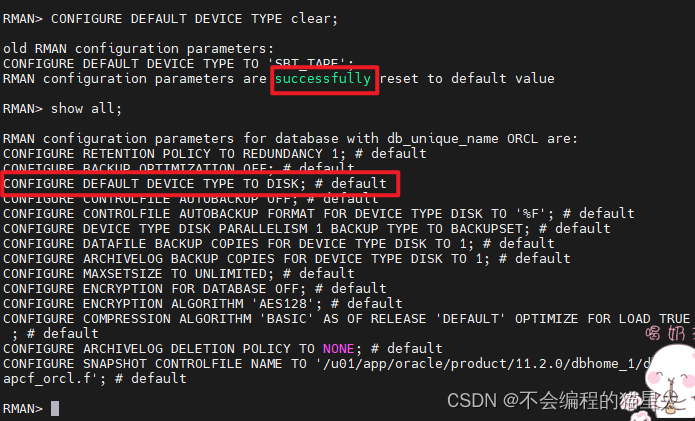
Oracle(2-9) Oracle Recovery Manager Overview and Configuration
文章目录 一、基础知识1、User Backup VS RMAN2、Restoring &Recovering DB 还原&恢复数据库3、Recovery Manager Features 管理恢复功能4、RMAN Components RMAN组件5、Repository1: Control File 存储库1:控制文件6、Channel Allocation 通道道分配7、Media Manageme…...
滑动验证码
先上图 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>滑动验证码</title><style>* {margin: 0;padding: 0;}.box {position: relative;width: 375px;margin: 100px a…...

数据爬取+可视化实战_告白气球_词云展示----酷狗音乐
一、前言 歌词上做文本分析,数据存储在网页上,需要爬取数据下来,词云展示在工作中也变得日益重要,接下来将数据爬虫与可视化结合起来,做个词云展示案例。 二、代码 # -*- coding:utf-8 -*- # 酷狗音乐 通过获取每首歌…...

rkmedia_vi_get_frame_test.c 代码解析
使用示例: 录像: rkmedia_vi_get_frame_test -a /etc/iqfiles/ -I 1 -o 1080.nv12 然后用yuvplayer.exe可以播放。 录像10帧: rkmedia_vi_get_frame_test -a /etc/iqfiles/ -I 1 -o 1080.nv12 -c 10 解析代码: #include <as…...

探究Kafka原理-3.生产者消费者API原理解析
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
