【算法刷题】Day9
文章目录
- 611. 有效三角形的个数
- 题干:
- 题解:
- 代码:
- LCR 179. 查找总价格为目标值的两个商品
- 题干:
- 题解:
- 代码:
- 1137. 第 N 个泰波那契数
- 题干:
- 原理:
- 1、状态表示(dp表里面的值所表示的含义)
- 2、状态转移方程(dp[i] 等于什么)
- 3、引初始化 (保证填表的时候不越界)
- 4、填文顺表 (为了填写当前状态的时候,所需的状态已经计算过了)
- 5、返回值 (题目要求 + 状态表示)
- 代码:
- 空间优化:
611. 有效三角形的个数

原题链接
题干:
首先看题干,非负整数数组,三元组数
所以,我们可知,这个数组最少有三个元素,这样才能组成三元组
在解题之前,我们补充一点:
给我们三个数,怎么判断是不是能不能构成三角形呢?
我们一般的判断都是任意两边之和大于第三边,但是如果在时间复杂度的位置上考虑,比三次太麻烦
这个时候,我们想,如果让这个数组是有序的,对比的这三个边是有序的,那么两个较短的边相加,大于第三边,是不是就可以说明前面两条边任意一条和后面的相加,都大于其余一条边呢?
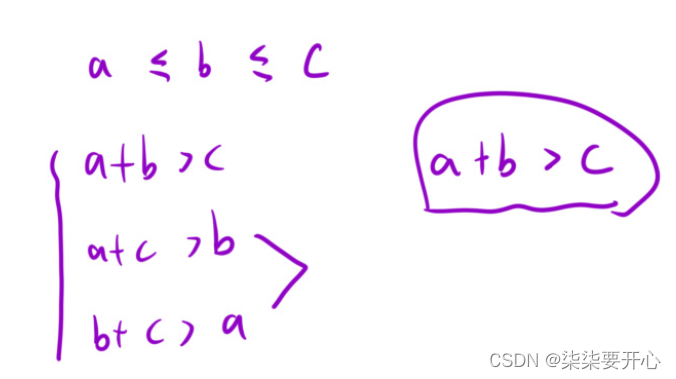
很明显,这样是可以的,所以我们的算法就进一步进行了优化
题解:
1、暴力枚举 O(N)
暴力算法就是写三个 for 循环嵌套,在最里面的一层 for 循环判断三个数是否能组成三角形
这个算法虽然可以算出,但是由于时间复杂度太高,会导致超时
2、利用单调性,使用双指针算法解决问题
(0)排序
(1)先固定最大的数
(2)在最大的数的左区间,使用双指正,快速统计出符合要求的三元组个数
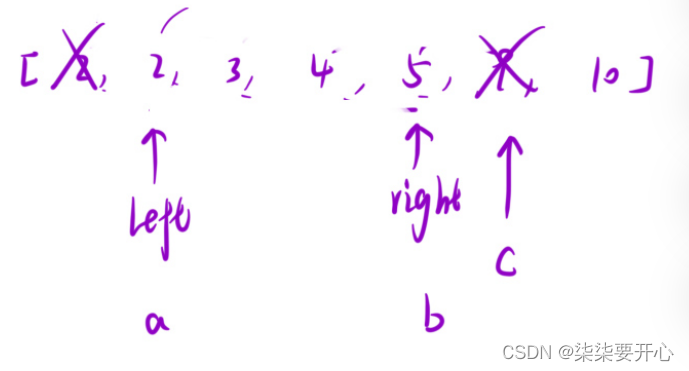
我们先看这个数组,我们先把最后一个数字固定,定义 left 和 right,
让left + right,如果大于 最后一个数字,那么left 右边的所有数字和 right 相加都大于,所以中间的统计下来,right –
如果小于,那么left++,再次判断
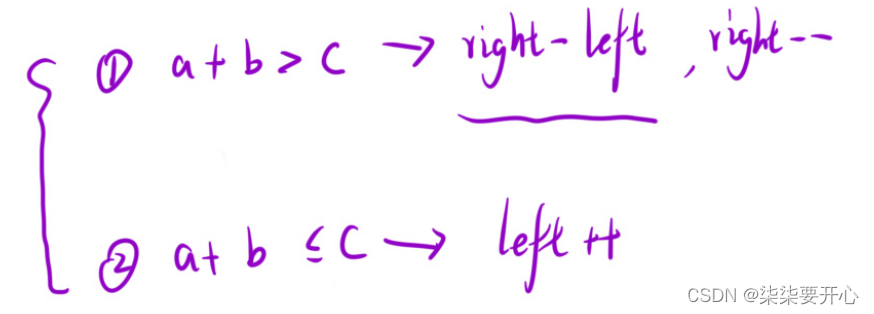
代码:
class Solution {public int triangleNumber(int[] nums) {//1.优化:排序Arrays.sort(nums);//2.利用双指针解决问题int ret = 0;int n = nums.length;for (int i = n - 1; i >= 2; i--) {//先固定最大的数//利用双指针快速统计处符合要求的三元组的个数int left = 0;int right = i-1;while (left < right) {if (nums[left] + nums[right] > nums[i]) {ret += right - left;right--;}else {left++;}}}return ret;}
}
LCR 179. 查找总价格为目标值的两个商品

原题链接
题干:
先看题干,升序数组,两个数相加等于 target
很好,这道题非常简单
题解:
1、暴力枚举 O(N2)
运用暴力枚举可以直接用两个 for 循环嵌套,然后再循环内部相加判断是不是和 target 相等
这个方法虽然很简单,但是时间复杂度过高,会超出时间
2、利用单调性,使用双指针解决问题
这个时候,我们依然使用我们非常熟悉的单调性和双指针
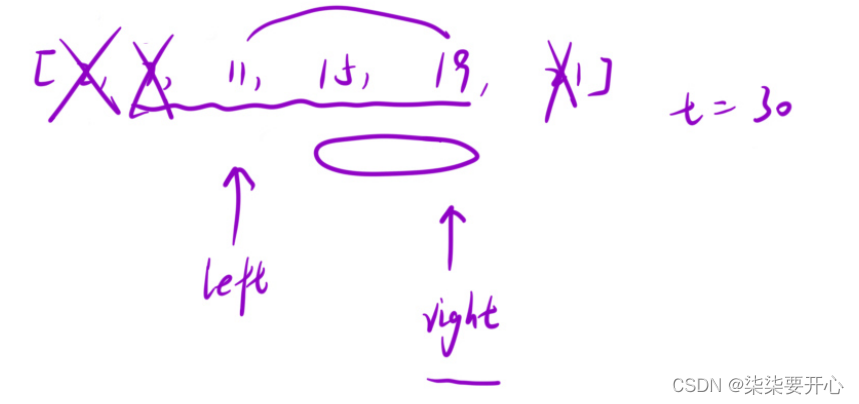
先判断left 和 right 相加
如果 大于 t ,right–
如果 小于 t ,left++
如果相等,直接返回
代码:
public int[] twoSum(int[] price, int target) {int left = 0;int right = price.length-1;while (left < right) {int sum = price[left] + price[right];if (sum > target) {right--;}else if (sum < target) {left++;}else {return new int[]{price[left],price[right]};}}return new int[]{0};}
1137. 第 N 个泰波那契数

原题链接
题干:
由题干可知
T0 = 0
T1 = 1
T2 = 1
Tn+3 = Tn + Tn+1 + Tn+2
可以变形为:Tn = Tn-3 + Tn-2 + Tn-1
原理:
1、状态表示(dp表里面的值所表示的含义)
由于我们在写动态规划问题的时候,需要用到dp表
dp表是怎么来的呢?
- 题目要求:本题 dp[i] 表示 第 i 个泰波那契数的值
- 经验 + 题目要求
- 分析问题的过程中,发现的重复子问题
2、状态转移方程(dp[i] 等于什么)
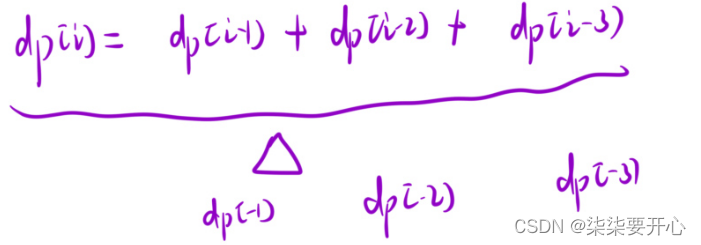
3、引初始化 (保证填表的时候不越界)

4、填文顺表 (为了填写当前状态的时候,所需的状态已经计算过了)
从左向右
5、返回值 (题目要求 + 状态表示)
dp [n]
代码:
public int tribonacci(int n) {//1.创建 dp 表//2.初始化//3.填表//4.返回值//先处理边界if(n == 0) {return 0;}if(n == 1 || n == 2) {return 1;}int[] dp = new int[n+1];dp[0] = 0;dp[1] = dp[2] = 1;for(int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];}return dp[n];}
空间优化:
这里我们用到的空间优化的方式是滚动数组
在解题的过程中发现,我们求 dp[i] 都是前三个数求和,不需要用到再往前的数
这个时候我们就可以拿三个数来存放,并且用后面的值改变前面的值
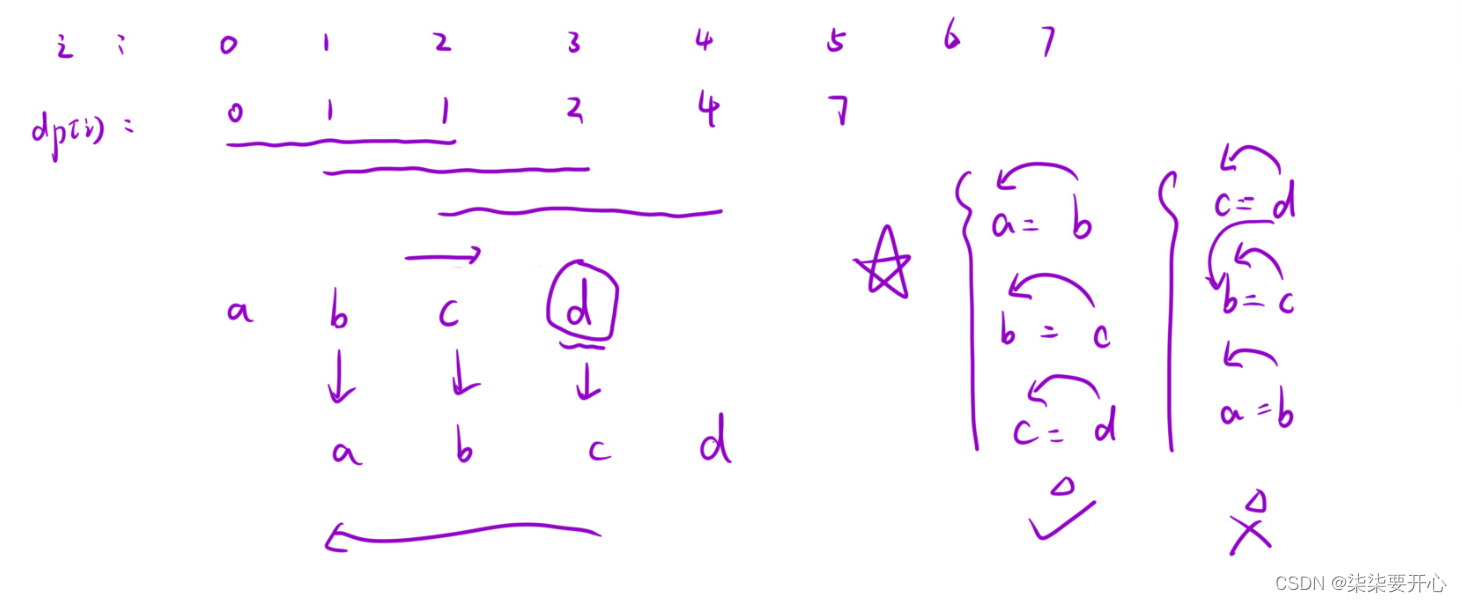
这个顺序是无法改变的,因为第二种方法,会把前面的值覆盖掉,导致出错
public int tribonacci(int n) {//空间优化//先处理边界if(n == 0) {return 0;}if(n == 1 || n == 2) {return 1;}int a = 0;int b = 1;int c = 1;int d = 0;for(int i = 3; i <= n; i++) {d = a + b + c;//滚动操作a = b;b = c;c = d;}return d;}
相关文章:

【算法刷题】Day9
文章目录 611. 有效三角形的个数题干:题解:代码: LCR 179. 查找总价格为目标值的两个商品题干:题解:代码: 1137. 第 N 个泰波那契数题干:原理:1、状态表示(dp表里面的值所…...

LangChain的函数,工具和代理(三):LangChain中轻松实现OpenAI函数调用
在我之前写的两篇博客中:OpenAI的函数调用,LangChain的表达式语言(LCEL)中介绍了如何利用openai的api来实现函数调用功能,以及在langchain中如何实现openai的函数调用功能,在这两篇博客中,我们都需要手动去创建一个结构比较复杂的函数描述变量…...

WiFi概念介绍
WiFi概念介绍 1. 什么是WLAN2. 什么是Wi-Fi3. Wi-Fi联盟4. WLAN定义范围5. WiFi协议体系6. 协议架构7. WiFi技术的发展7.1 IEEE802.117.2 802.11标准和补充 8. 术语 1. 什么是WLAN Wireless Local Area Network,采用802.11无线技术进行互连的一组计算机和相关设备。…...
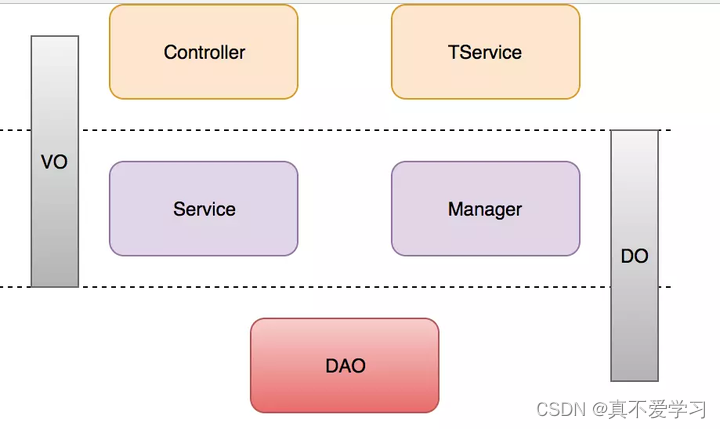
如何优雅的进行业务分层
1.什么是应用分层 说起应用分层,大部分人都会认为这个不是很简单嘛 就controller,service, mapper三层。 看起来简单,很多人其实并没有把他们职责划分开,在很多代码中,controller做的逻辑比service还多,service往往当…...

C++的std命名空间
总以为自己懂了,可是仔细想想,多问自己几个问题,发现好像又不是很清楚 命名空间(Namespace)是C中一种用于解决命名冲突问题的机制,它能够将全局作用域划分为若干个不同的区域,每个区域内可以有…...

unity学习笔记
一、射线检测 如何让鼠标点击某个位置,游戏角色就能移动到该位置? 实现的原理分析:我们能看见游戏的东西就是摄像机拍摄到的东西,所以摄像机的镜平面就是当前能看到的了。 那接下来我们可以让摄像机发射一条射线,鼠标…...

使用SpringBoot和ZXing实现二维码生成与解析
一、ZXing简介 ZXing是一个开源的,用Java实现的多种格式的1D/2D条码图像处理库。它包含了用于解析多种格式的1D/2D条形码的工具类,目标是能够对QR编码,Data Matrix, UPC的1D条形码进行解码。在二维码编制上,ZXing巧妙地利用构成计…...
C++模板—函数模板、类模板
目录 一、函数模板 1、概念 2、格式 3、实例化 4、模板参数的匹配 二、类模板 1、定义格式 2、实例化 交换两个变量的值,针对不同类型,我们可以使用函数重载实现。 void Swap(double& left, double& right) {double tmp left;left ri…...

Monkey
一、Monkey的概念 “猴子测试”是指没有测试经验的人甚至对计算机根本不了解的人(就像猴子一样)不需要知道程序的任何用户交互方面的知识,如果给他一个程序,他就会针对他看到的界面进行操作,其操作是无目的的、乱点乱按…...
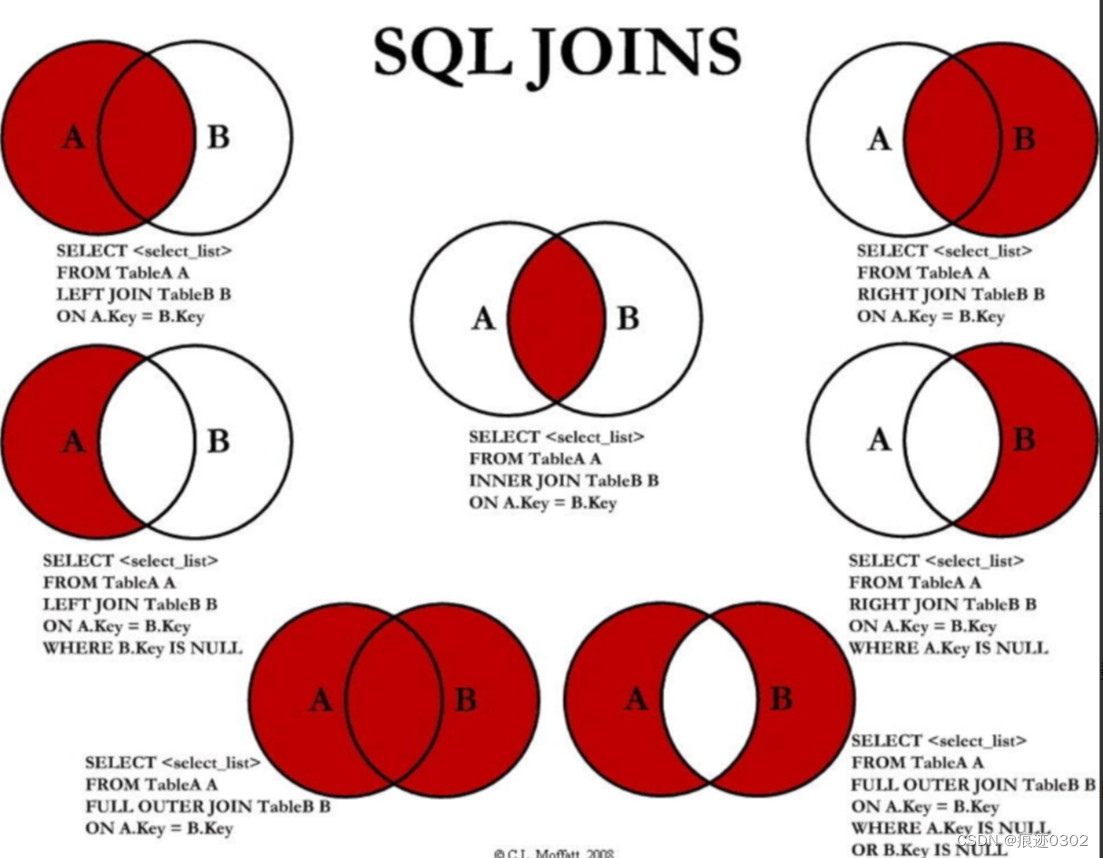
SQL中left join、right join、inner join等的区别
一张图可以简洁明了的理解出left join、right join、join、inner join的区别: 1、left join 就是“左连接”,表1左连接表2,以左为主,表示以表1为主,关联上表2的数据,查出来的结果显示左边的所有数据&#…...

算法学习—排序
排序算法 一、选择排序 1.算法简介 选择排序是一个简单直观的排序方法,它的工作原理很简单,首先从未排序序列中找到最大的元素,放到已排序序列的末尾,重复上述步骤,直到所有元素排序完毕。 2.算法描述 1ÿ…...

在Pycharm中创建项目新环境,安装Pytorch
在python项目中,很多项目使用的各类包的版本是不一致的。所以我们可以对每个项目有专属于它的环境。所以这个文章就是教你如何创建新环境。 一、创建新环境 首先我们需要去官网下载conda。然后在Pycharm下面添加conda的可执行文件。 用conda创建新环境。 二、…...

linux里source、sh、bash、./有什么区别
1、source source a.sh 在当前shell内去读取、执行a.sh,而a.sh不需要有"执行权限" source命令可以简写为"." . a.sh 注意:中间是有空格的。 2、sh/bash sh a.sh bash a.sh 都是打开一个subshell去读取、执行a.sh,而a.…...
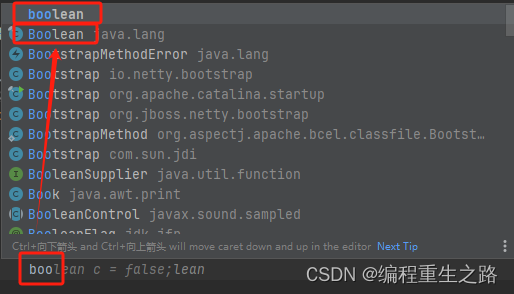
IDEA编译器技巧-提示词忽略大小写
IDEA编译器技巧-提示词忽略大小写 写代码时,每次创建对象都要按住 Shift 字母 做大写开头, 废手, 下面通过编译器配置解放Shift 键 setting -> Editor -> General -> Code Completion -> Match case 把这个√去掉, 创建对象就不需要再按住 Shift 键 示例: 1.…...
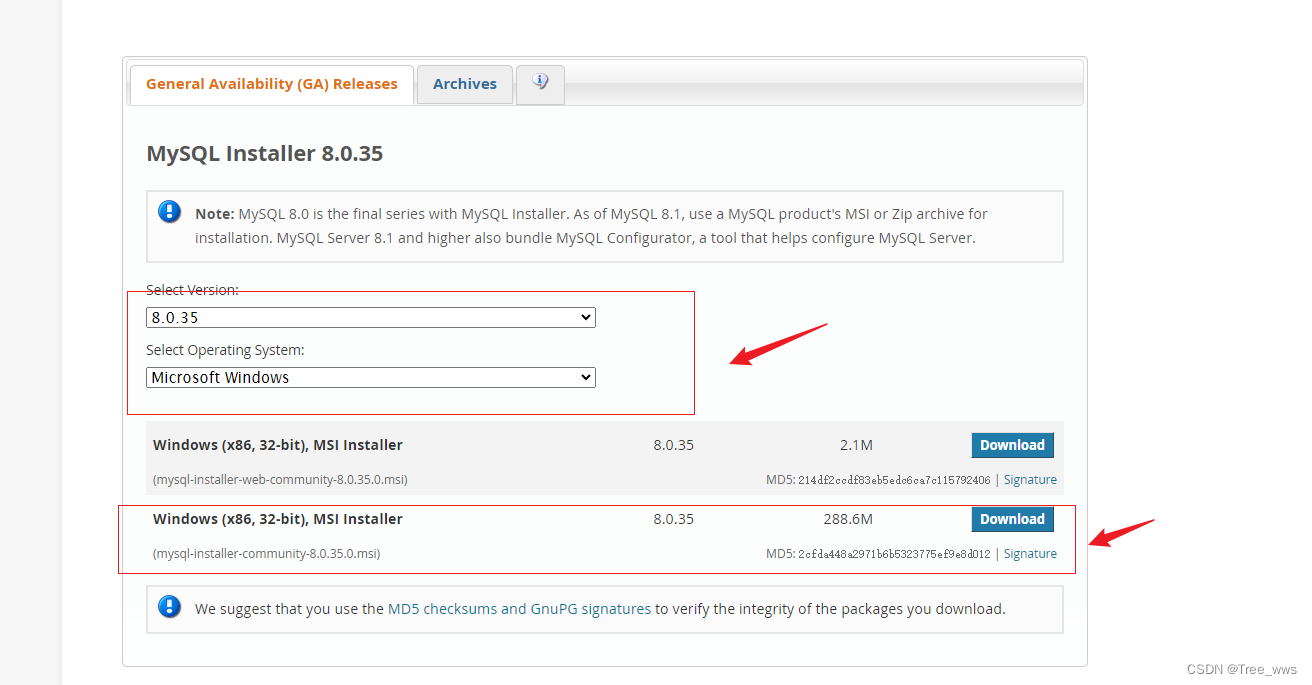
【MySQL】MySQL安装 环境初始化
MySQL安装 MYSQL官网 安装完成后,傻瓜下一步即可 配置一下环境变量即可 (1) 初始化MySQL, 管理员身份运行 mysqld --initialize-insecure(2) 注册 mysqld mysqld -install# 如果记录以前的版本执行下面指令 mysqld -remove(3) 启动MySQL服务 // 启动mysql服务 net start …...

C# IList 与List区别二叉树的层序遍历
IList 接口: IList 是一个接口,定义了一种有序集合的通用 API。继承自 ICollection 接口和IEnumerable<T>,是所有泛型列表的基接,口它提供了对列表中元素的基本操作,如添加、删除、索引访问等。IList 不是一个具…...
助力android面试2024【面试题合集】
转眼间,2023年快过完了。今年作为口罩开放的第一年大家的日子都过的十分艰难,那么想必找工作也不好找,在我们android开发这一行业非常的卷,在各行各业中尤为突出。android虽然不好过,但不能不吃饭吧。卷归卷但是还得干…...

【动态规划】LeetCode-62.不同路径
🎈算法那些事专栏说明:这是一个记录刷题日常的专栏,每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目,在这立下Flag🚩 🏠个人主页:Jammingpro 📕专栏链接&…...
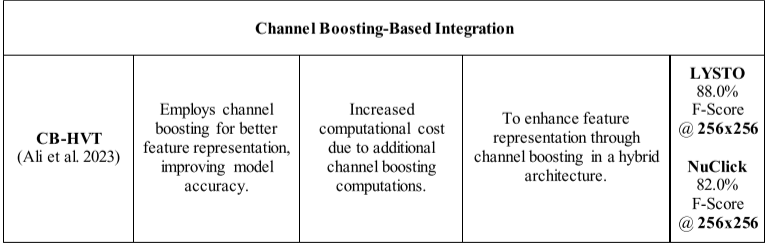
对 Vision Transformers 及其基于 CNN-Transformer 的变体的综述
A survey of the Vision Transformers and its CNN-Transformer based Variants 摘要1、介绍2、vit的基本概念2.1 patch嵌入2.2 位置嵌入2.2.1 绝对位置嵌入(APE)2.2.2 相对位置嵌入(RPE)2.2.3卷积位置嵌入(CPE) 2.3 注意力机制2.3.1多头自我注意(MSA) 2.4 Transformer层2.4.1 …...
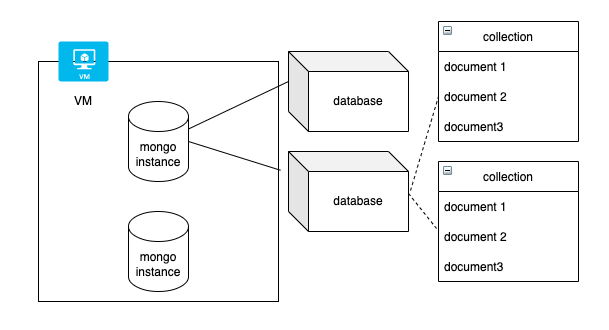
MongoDB简介
数据库,顾名思义,是保存数据的地方。中华文化博大精深,短短3个文字,就定义了一个强大的数据管理和读写方式出来。数据库,管理的对象是数据。称为库,表示数据在库中有组织,相互之间有微妙的关系。…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
