算法学习—排序
排序算法
一、选择排序
1.算法简介
选择排序是一个简单直观的排序方法,它的工作原理很简单,首先从未排序序列中找到最大的元素,放到已排序序列的末尾,重复上述步骤,直到所有元素排序完毕。
2.算法描述
1)假设未排序序列的第一个是最大值,记下该元素的位置,从前往后比较
2)若某个元素比该元素大,覆盖之前的位置
3)重复第二个步骤,直到找到未排序的末尾
4)将未排序元素的第一个元素和最大元素交换位置
5)重复前面几个步骤,直到所有元素都已经排序。
3.算法分析
选择排序的交换操作次数最好情况已经有序为0次,最坏情况逆序n-1次,因此交换操作次数位于0(n-1)次之间;比较操作次数(n-1+…+2+1+0)为n(n-1)/2次;交换元素赋值操作为3次,逆序需要n-1趟交换,因此,赋值操作位于03(n-1)次之间。由于需要交换位置,所以肯定是不稳定的。
时间复杂度均为o(n^2) 空间复杂度为o(1) 不稳定
4.代码实现
//选择排序
function selsetSort(arr){var len = arr.length;for(var i=0;i<len-1;i++){for(var j=i+1;j<len;j++){if(arr[i] > arr[j]){//寻找最小值var temp = arr[i];arr[i] = arr[j];arr[j] = temp;}}}return arr;
}
二、冒泡排序
1.算法简介
列表每两个相邻的数进行比较,如果前面的数比后面的数大,则交换这两个数,一轮排序完成后,则无序区减少一个数,有序区增加一个数。
2.算法描述
1)快速排序的特点就是随机设置一个基准点,比如是数组的第一个元素,然后数组的其他元素就跟这个基准线进行对比,比基准线大的放在左边,比基准线小的放在右边
2)再设置一个基准线,再这样小的放左边,大的放右边,递归。
3.算法分析
平均时间复杂度O(nn) 、最好情况O(n)、最差情况O(nn)
空间复杂度O(1) 稳定
4.代码实现
function sort(arr){let len = arr.length;for (let i = 0; i < len - 1 ; i++) {// 用来标记在一轮冒泡过程中有无交换过let flag = false;for (let j = 0; j < len - i; j++) {if(arr[j] > arr[j+1]){// 交换两个数let temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;flag = true;}}// 如果在一轮冒泡过程中没有交换过,说明此时的列表已经是排序好的了,直接结束循环if(!flag){return;}} }
let arr = [2,3,1,4,8,7,9,6];
this.sort(arr;
console.log(arr);
三、插入排序
1.算法简介
所谓插入排序,就是把最小的(或者最大的),一次次插入到最前面,从而达到排序的效果
2.算法描述
刚开始将整个数组看作一个无序区,每一轮拿无序区的第一数与有序区的数从后往前依次进行比较,遇到更大的数则交换,每一轮排序完成后,有序区增加一个数,无序区减少一个数。
3.算法分析
时间复杂度是O(n*n) 空间复杂度为o(1) 稳定
4.代码实现
function sort(arr){let len = arr.length;for (let i = 1; i < len; i++) {for (let j = i - 1; j >= 0 ; j--) {if(arr[j] > arr[j+1]){let temp = arr[j+1]arr[j+1] = arr[j]arr[j] = temp} } }
},
四、快速排序
1.算法简介
采用“分治”的思想,对于一组数据,选择一个基准元素(base),通常选择第一个或最后一个元素,通过第一轮扫描,比base小的元素都在base左边,比base大的元素都在base右边,再有同样的方法递归排序这两部分,直到序列中所有数据均有序为止。快速排序算法的性能比冒泡、选择排序都要好,和归并排序一样,是一个可以用于实战的算法。
2.算法描述
1)快速排序的特点就是随机设置一个基准点,比如是数组的第一个元素,然后数组的其他元素就跟这个基准线进行对比,比基准线大的放在左边,比基准线小的放在右边
2)再设置一个基准线,再这样小的放左边,大的放右边,递归。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为o(logn) 不稳定
4.代码实现
function sort(arr,l,r){if(l < r){let i = l;let j = r;let mid = arr[l];while(i < j){while(arr[j] > mid && i < j){j--;}arr[i] = arr[j];while(arr[i] < mid && i < j){i++;}arr[j] = arr[i];}arr[i] = midthis.test(arr,l,i-1)this.test(arr,i+1,j)return arr}else{return}}, // 测试数据
let arr = [2,3,1,4,8,7,9,6];
let res = this.sort(arr,0,7);
console.log(res);
五、归并排序
1.算法简介
使用分而治之的概念对给定的元素列表进行排序。它将问题分解为较小的子问题,直到它们变得足够简单以至可以直接解决为止。
2.算法描述
1)将给定的列表分为两半(如果列表中的元素数为奇数,则使其大致相等)。
2)以相同的方式继续划分子数组,直到只剩下单个元素数组。
3)从单个元素数组开始,合并子数组,以便对每个合并的子数组进行排序。
4)重复第 3 步单元,直到最后得到一个排好序的数组。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为O(n) 稳定
4.代码实现
function sort(arr){if(arr && arr.length > 1){const mid = Math.floor(arr.length/2)const left = arr.slice(0,mid)const right = arr.slice(mid);return this.merge(this.sort(left), this.sort(right))}return arr
},
function merge(leftList, rightList){const newList = [];const leftLength = leftList && leftList.length;const rightLength = rightList && rightList.length;let i = 0;let j = 0;while (i < leftLength && j < rightLength) {if (leftList[i] < rightList[j]) {newList.push(leftList[i++]);} else {newList.push(rightList[j++]);}}while (i < leftLength) {newList.push(leftList[i++]);}while (j < rightLength) {newList.push(rightList[j++]);}return newList;
},
六、堆排序
1.算法简介
堆是一种特殊的完全二叉树,堆分为大根堆和小根堆,满足任一节点都比其孩子节点大的一个完全二叉树就是大根堆,满足任一节点都比其孩子节点小的一个完全二叉树就是小根堆。
2.算法描述
首先构造一个大根堆(此时整个堆是无序区),然后将堆顶的元素取出放到有序区(也就是数组的最后),然后将堆的最后一个元素(也就是无序区的最后一个元素)放到堆顶,堆就少了一个元素,此时通过一次向下调整重新使堆有序,调整后的堆顶就是整个数组的第二大元素,然后重复之前的操作依次将元素放到有序区,直到堆变空,便可得到排序好的数组。
3.算法分析
时间复杂度是O(nlogn) 空间复杂度为O(1) 不稳定
4.代码实现
function sort(list) {if (list && list.length > 1) {const len = list.length;// 首先构造大根堆,从最后一个不是叶子节点的节点开始遍历,从后往前依次进行向下调整for (let i = Math.floor((len-2)/2); i>=0; i--) {sift(list, i, len-1);}// 然后将堆的第一元素与有序区的第一个元素进行交换,此时有序区增加一个,无序区减少一个,再进行一次堆的向下调整,然后重复上述操作,最终使整个数组有序for(let i = len-1; i>=0; i--){const m = list[0];list[0] = list[i];list[i] = m;sift(list, 0, i-1);} }
}/**
* 堆的向下调整
* 先从根节点开始,如果孩子节点比父节点大,则将该孩子节点赋值给父节点
* 然后指针指向下一层,重复上面的操作,直到找到孩子节点没有比父节点大的节点,终止循环
* 最后将原始的根节点赋值给当前父节点
*/
function sift(li, low, high) {const tmp = li[low]; // 缓存根节点let i = low; // 当前的父节点,最开始指向根节点let j = i*2+1; // 当前的孩子节点,最开始指向根节点的左孩子节点while (j <= high) {// 如果有右孩子节点且比左孩子节点大,则j指向右孩子节点if (j+1 <= high && li[j+1] > li[j]) {j++;}if (li[j] > tmp) {li[i] = li[j]; // 将较大的孩子节点赋值给父节点i = j; // i指向下一层j = i*2 +1;} else {break; // 如果当前子节点没有比原始根节点大,结束循环}}li[i] = tmp; // 最后将原始的根节点赋值给当前父节点
}
总结

相关文章:

算法学习—排序
排序算法 一、选择排序 1.算法简介 选择排序是一个简单直观的排序方法,它的工作原理很简单,首先从未排序序列中找到最大的元素,放到已排序序列的末尾,重复上述步骤,直到所有元素排序完毕。 2.算法描述 1ÿ…...

在Pycharm中创建项目新环境,安装Pytorch
在python项目中,很多项目使用的各类包的版本是不一致的。所以我们可以对每个项目有专属于它的环境。所以这个文章就是教你如何创建新环境。 一、创建新环境 首先我们需要去官网下载conda。然后在Pycharm下面添加conda的可执行文件。 用conda创建新环境。 二、…...

linux里source、sh、bash、./有什么区别
1、source source a.sh 在当前shell内去读取、执行a.sh,而a.sh不需要有"执行权限" source命令可以简写为"." . a.sh 注意:中间是有空格的。 2、sh/bash sh a.sh bash a.sh 都是打开一个subshell去读取、执行a.sh,而a.…...
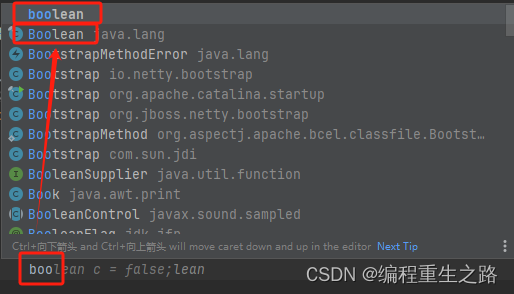
IDEA编译器技巧-提示词忽略大小写
IDEA编译器技巧-提示词忽略大小写 写代码时,每次创建对象都要按住 Shift 字母 做大写开头, 废手, 下面通过编译器配置解放Shift 键 setting -> Editor -> General -> Code Completion -> Match case 把这个√去掉, 创建对象就不需要再按住 Shift 键 示例: 1.…...
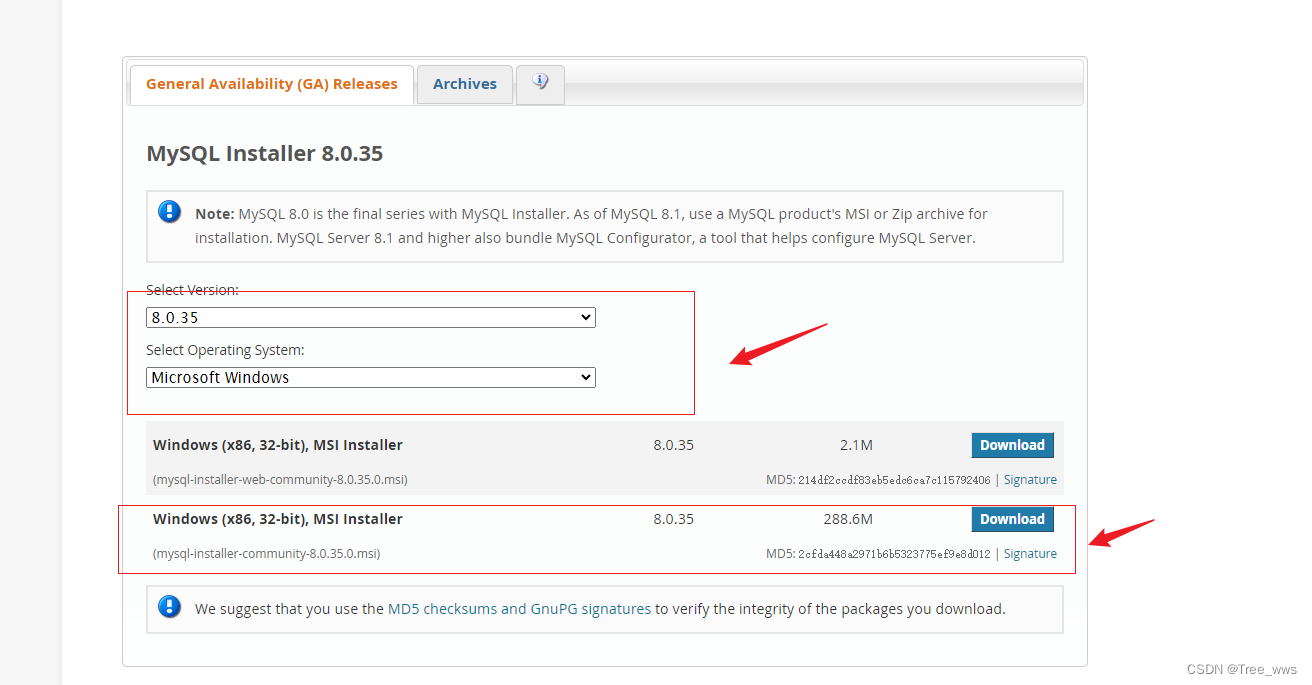
【MySQL】MySQL安装 环境初始化
MySQL安装 MYSQL官网 安装完成后,傻瓜下一步即可 配置一下环境变量即可 (1) 初始化MySQL, 管理员身份运行 mysqld --initialize-insecure(2) 注册 mysqld mysqld -install# 如果记录以前的版本执行下面指令 mysqld -remove(3) 启动MySQL服务 // 启动mysql服务 net start …...

C# IList 与List区别二叉树的层序遍历
IList 接口: IList 是一个接口,定义了一种有序集合的通用 API。继承自 ICollection 接口和IEnumerable<T>,是所有泛型列表的基接,口它提供了对列表中元素的基本操作,如添加、删除、索引访问等。IList 不是一个具…...
助力android面试2024【面试题合集】
转眼间,2023年快过完了。今年作为口罩开放的第一年大家的日子都过的十分艰难,那么想必找工作也不好找,在我们android开发这一行业非常的卷,在各行各业中尤为突出。android虽然不好过,但不能不吃饭吧。卷归卷但是还得干…...

【动态规划】LeetCode-62.不同路径
🎈算法那些事专栏说明:这是一个记录刷题日常的专栏,每个文章标题前都会写明这道题使用的算法。专栏每日计划至少更新1道题目,在这立下Flag🚩 🏠个人主页:Jammingpro 📕专栏链接&…...
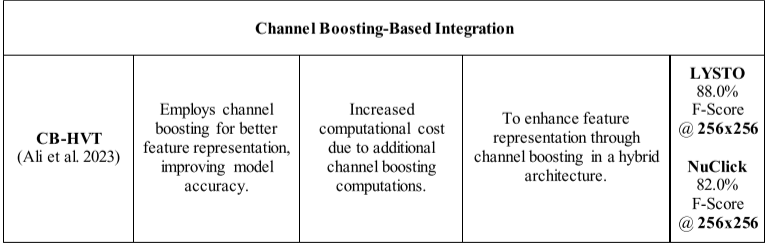
对 Vision Transformers 及其基于 CNN-Transformer 的变体的综述
A survey of the Vision Transformers and its CNN-Transformer based Variants 摘要1、介绍2、vit的基本概念2.1 patch嵌入2.2 位置嵌入2.2.1 绝对位置嵌入(APE)2.2.2 相对位置嵌入(RPE)2.2.3卷积位置嵌入(CPE) 2.3 注意力机制2.3.1多头自我注意(MSA) 2.4 Transformer层2.4.1 …...
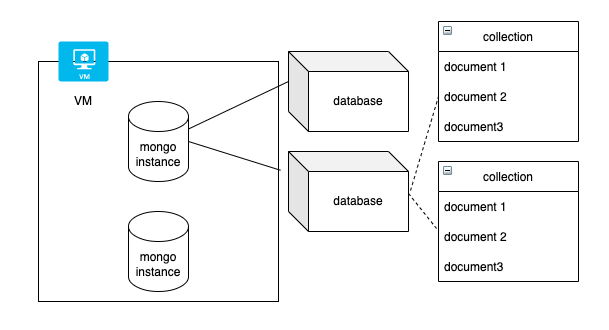
MongoDB简介
数据库,顾名思义,是保存数据的地方。中华文化博大精深,短短3个文字,就定义了一个强大的数据管理和读写方式出来。数据库,管理的对象是数据。称为库,表示数据在库中有组织,相互之间有微妙的关系。…...

尚硅谷hadoop3.x课程部分资料文件下载,jdk,hadoopjar包
jdk文件百度云下载: 链接:https://pan.baidu.com/s/1MCiGRzOZY8rAFpRJwA3tdw 提取码:kphl hadoop的jar包: 最新版官网链接: Index of /dist/hadoop/core/stable (apache.org) 百度云下载,3.3.3版…...

vue el-radio-group多选封装及使用
基于Element UI库的Vue组件,实现了一个单选/多选框组合的效果,可以根据 type 属性的不同值来切换单选框(默认)和按钮式单选框/多选框。 创建组件index.vue (src/common-ui/radioGroup/index.vue) <template><el-radio-g…...
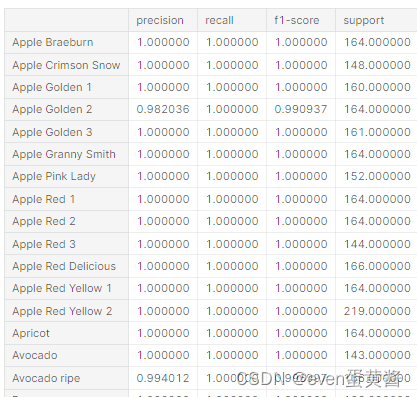
Kaggle-水果图像分类银奖项目 pytorch Densenet GoogleNet ResNet101 VGG19
一些原理文章 卷积神经网络基础(卷积,池化,激活,全连接) - 知乎 PyTorch 入门与实践(六)卷积神经网络进阶(DenseNet)_pytorch conv1x1_Skr.B的博客-CSDN博客GoogLeNet网…...
TPLink-Wr702N 通过OpenWrt系统打造打印服务器实现无线打印
最近淘到了一个TPLink-Wr702N路由器,而且里面已经刷机为OpenWrt系统了,刚好家里有一台老的USB打印机,就想这通过路由器将打印机改为无线打印机,一番折腾后,居然成功了,这里记录下实现过程,为后面…...

[UGUI]实现从一个道具栏拖拽一个UI道具到另一个道具栏
在Unity游戏开发中,实现UI道具的拖拽功能是一项常见的需求。本文将详细介绍如何使用Unity的UGUI系统和事件系统,实现从一个道具栏拖拽一个UI道具到另一个道具栏的功能。 一、准备工作 首先,你需要在Unity中创建两个道具栏和一些UI道具。道具…...

微服务--08--Seata XA模式 AT模式
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 分布式事务Seata 1.XA模式1.1.两阶段提交1.2.Seata的XA模型1.3.优缺点 AT模式2.1.Seata的AT模型2.2.流程梳理2.3.AT与XA的区别 分布式事务 > 事务–01—CAP理论…...

Doris 数据导入一:Broker Load 方式
1.Doris导入数据的方式总结 导入(Load)功能就是将用户的原始数据导入到 Doris 中。导入成功后,用户即可通过 Mysql 客户端查询数据。为适配不同的数据导入需求,Doris 系统提供了6种不同的导入方式。每种导入方式支持不同的数据源,存在不同的使用方式(异步,同步)。 所有…...

docker踩坑记录:docker容器创建doris容器间无法通讯问题
背景: 开发大数据平台,使用doris作为数据仓储,使用docker做集群部署,先进行开发环境搭建,环境为BE1;FE1,原来使用官方例子,但是官方例子是创建了一个bridge使用172.20.80.0/24通讯,…...

springboot+java校园自助洗衣机预约系统的分析与设计ssm+jsp
洗衣服是每个人都必须做的事情,而洗衣机更成为了人们常见的电器,但是单个洗衣机价格不菲,如果每人都买,就会造成资源的冗余。所有就出现了公用设备,随着时代的发展,很多公用都开始向着无人看守的自助模式经…...

TCP简介及特性
1. TCP协议简介 TCP是Transmission Control Protocol的简称,中文名是传输控制协议。它是一种面向连接的、可靠的、基于IP的传输层协议。两个TCP应用之间在传输数据的之前必须建立一个TCP连接,TCP采用数据流的形式在网络中传输数据。TCP为了保证报文传输的…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
