蓝桥杯-本质上升序列
没有白走的路,每一步都算数🎈🎈🎈
题目描述:
小蓝特别喜欢单调递增的事物
在一个字符串中如果取出若干个字符,按照在原来字符串中的顺序排列在一起,组成的新的字符串如果是单调递增的,那么则称这个字符串为一为一个单调递增子序列。但是对于lanqiao字符串,
单调子序列可以有l,a,n,q,i,o;
ao,io,q,nq,no,ai,aq,an,aio,ano,anq;
lo,ln,lq,lnq
但是,第一个‘a’能够和‘o’组成一个单调递增子序列,倒数第一个‘a’也能和‘o’组成一个子序列,我们称这样的序列本质上是相同的。求问总共有多少本质不同的单调上升子序列
输入描述:
输入一个字符串s,字符串总共有4行,每行50个字母,总共有200个字母。试求这个字符串的本质上升序列总共有多少?
样例输入输出:
样例输入:
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
算法设计:
从后往前找,一个字符一个字符累加。遇到不相同的并且后面字母比前面大的就累加,遇到相同的则需要减去相同的字符串。
import os
import sys
s = "tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl"
dp = [0]*200
n = len(s)
cnt = 0
for i in range(n-1,-1,-1):dp[i] = 1for j in range(i+1,n):if s[i]<s[j]:dp[i]+=dp[j]elif s[i]==s[j]:dp[i]-=dp[j]cnt+=dp[i]
print(cnt)每日一句
摘自《平凡的世界》:
人生啊,是这样不可预测,没有永恒的痛苦,也没有永恒的幸福,生活像流水一般,有时是那么平展,有时又是那么曲折。
相关文章:

蓝桥杯-本质上升序列
没有白走的路,每一步都算数🎈🎈🎈 题目描述: 小蓝特别喜欢单调递增的事物 在一个字符串中如果取出若干个字符,按照在原来字符串中的顺序排列在一起,组成的新的字符串如果是单调递增的…...

synchronized锁重入验证
文章目录synchronized锁重入验证1. 可重入锁2. synchronized锁重入2.1 本类同步方法内部调用本类其它同步方法2.2 子类同步方法内部调用父类的同步方法2.3 A类的同步方法内部调用B类的同步方法3. synchronized修饰方法写法synchronized锁重入验证 1. 可重入锁 可重入锁&#…...

超简单的计数排序!!
假设给定混乱数据为:3,0,1,3,6,5,4,2,1,9。 下面我们将通过使用计数排序的思想来完成对上面数据的排序。(先不谈负数) 计数排序 该排序的思路和它的名字一样…...

发现新大陆——原来软件开发根本不需要会编码(看我10分钟应用上线)
目录 一、前言 二、官网基础功能及搭建 三、体验过程 01、连接数据源 02、设计表单 03、流程设计 04、图表呈现 05、组织架构设置 五、效率评价 六、小结 一、前言 众所周知,每家公司在发展过程中都需要构建大量的内部系统, 如运营使用的用户…...

【Leedcode】栈和队列必备的面试题(第二期)
【Leedcode】栈和队列必备的面试题(第二期) 文章目录【Leedcode】栈和队列必备的面试题(第二期)一、题目(用两个队列实现栈)二、思路图解1.定义两个队列2.初始化两个队列3.往两个队列中放入数据4.两个队列出…...
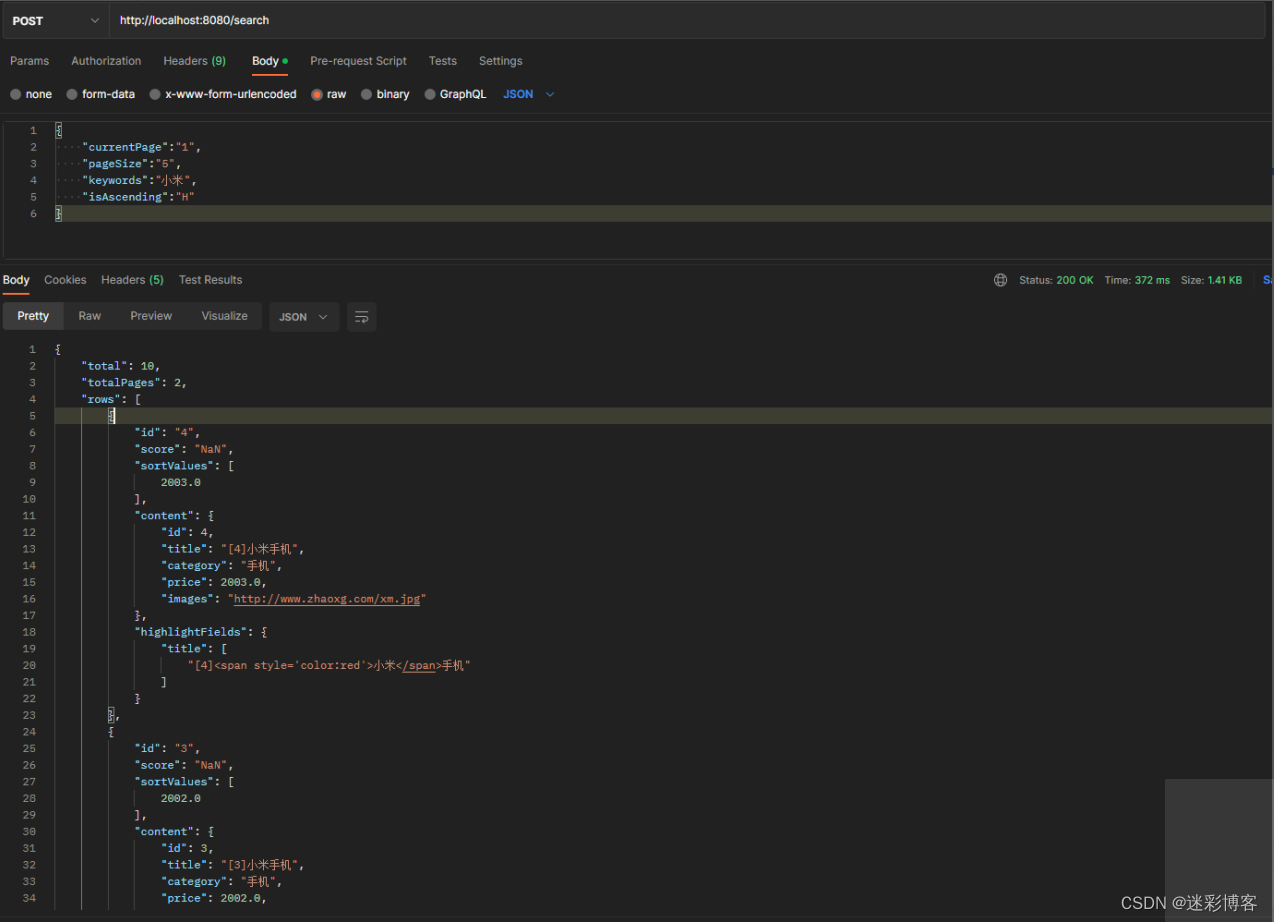
Elasticsearch实战之(商品搜索API实现)
Elasticsearch实战之(商品搜索API实现) 1、案例介绍 某医药电商H5商城基于Elasticsearch实现商品搜索 2、案例分析 2.1、数据来源 商品库 - 平台运营维护商品库 - 供应商维护 2.2、数据同步 2.2.1、同步双写 写入 MySQL,直接也同步往…...
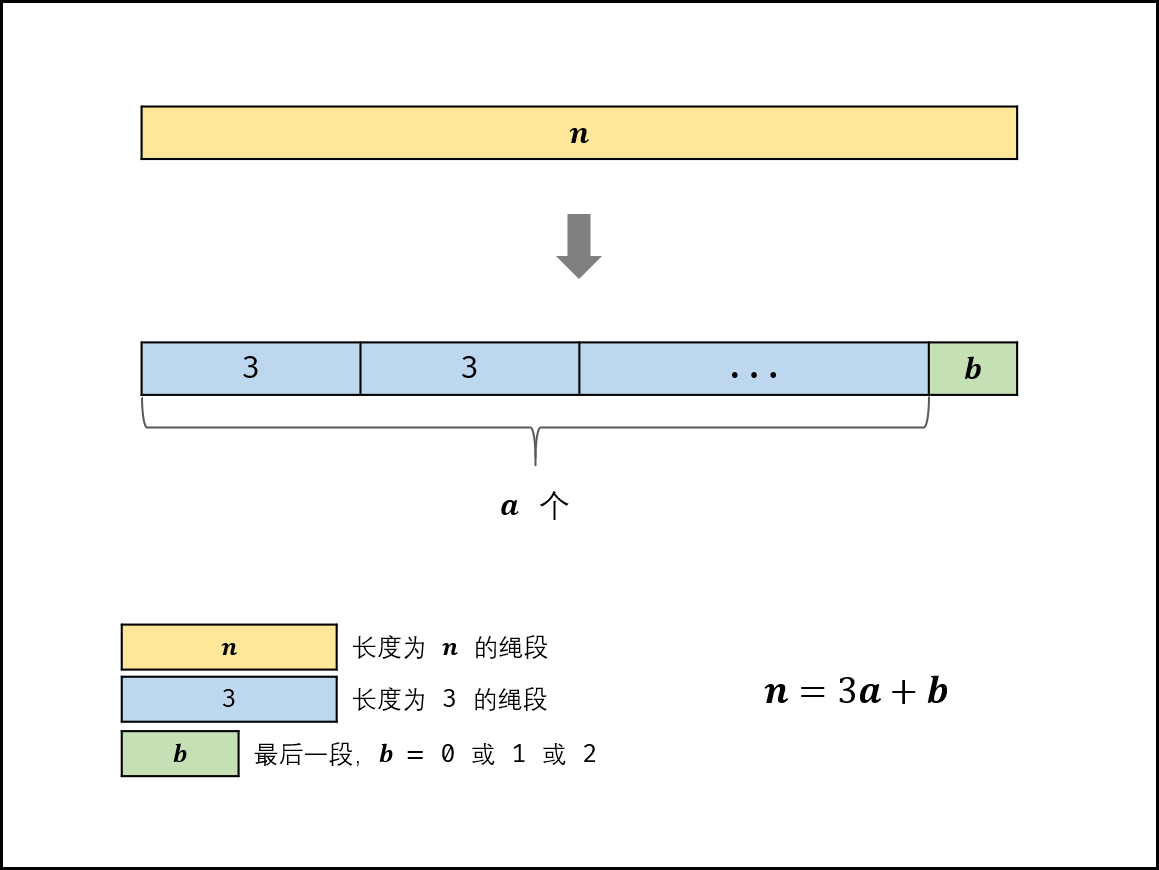
剑指 Offer 14-剪绳子
摘要 剑指 Offer 14- I. 剪绳子 剑指 Offer 14- II. 剪绳子 II 343. 整数拆分 一、动态规划解析 这道题给定一个大于1的正整数n,要求将n 拆分成至少两个正整数的和,并使这些正整数的乘积最大化,返回最大乘积。令x是拆分出的第…...
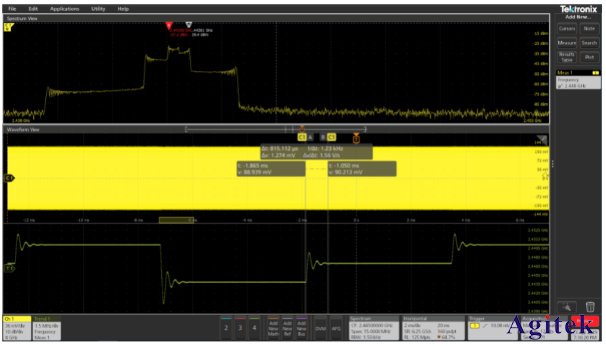
泰克示波器|MSO64示波器的应用
泰克新一代示波器MSO64为实例来讲解时频域信号分析技术。MSO64采用全新TEK049平台,不仅实现了4通道同时打开时25GS/s的高采样率,而且实现了12-bit高垂直分辨率。同时,由于采用了新型低噪声前端放大ASIC—TEK061,大大降低了噪声水平…...
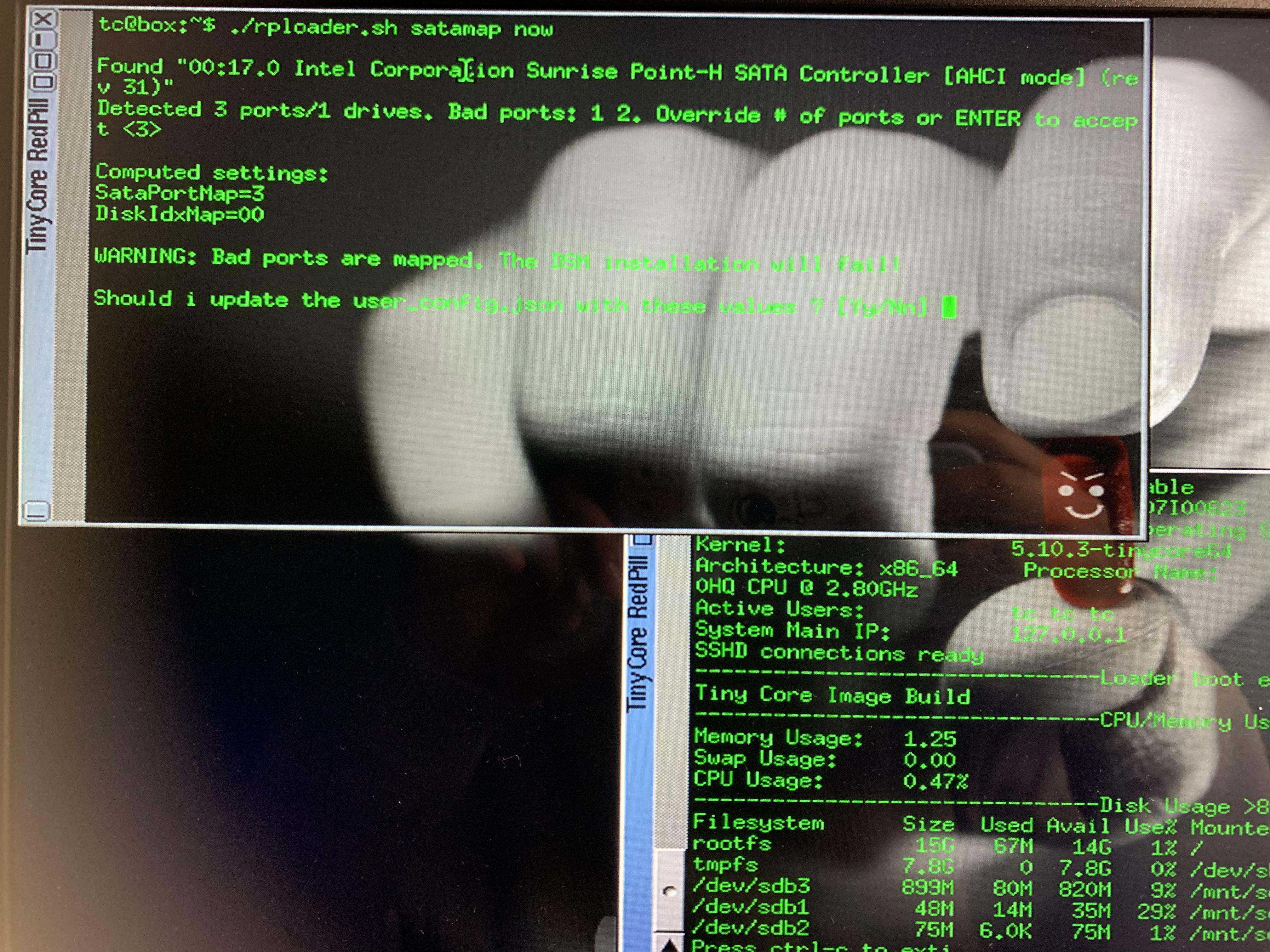
1.4 黑群晖安装:SataPortMap和DiskIdxMap两种获取方式
tinycore及安装工具下载:工具:链接:https://pan.baidu.com/s/1CMLl6waOuW-Ys2gKZx7Jgg?pwdchct提取码:chcttinycore:链接:https://pan.baidu.com/s/19lchzLj-WDXPQu2cEcskBg?pwddcw2 提取码:d…...
JVM虚拟机概述(2)
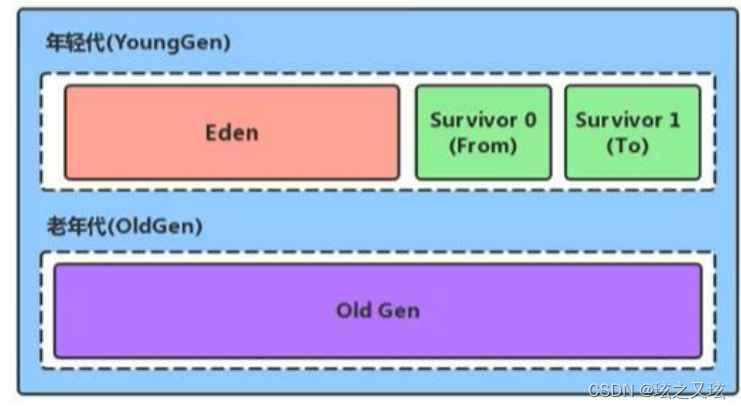
3.JVM 运行时数据区 3.1.1 程序计数器(Program Counter Register) 是一块很小的内存空间,用来记录每个线程运行的指令位置,是线程私有的,每个线程都拥有一个程序计数器,生命周期与线程一致,是运行时数据区中唯一一个不…...

Intel CSME 简述
SME 算是 Intel X86 PC 上最神秘的部分了,本文根据 us-19-Hasarfaty-Behind-The-Scenes-Of-Intel-Security-And-Manageability-Engine 一文写成。讲述内容无法证伪,各位随便听听即可,了解这些能够帮助BIOS 工程师更好的理解一些操作的实现。文章基于 Intel 第八代第九代CPU(…...

复位理论基础
先收集资料,了解当前常用的基础理论和实现方式 复位 初始化微控制器内部电路 将所有寄存器恢复成默认值确认MCU的工作模式禁止全局中断关闭外设将IO设置为高阻输入状态等待时钟趋于稳定从固定地址取得复位向量并开始执行 造成复位的原因 有多种引起复位的因素&…...
Python基础知识——列表
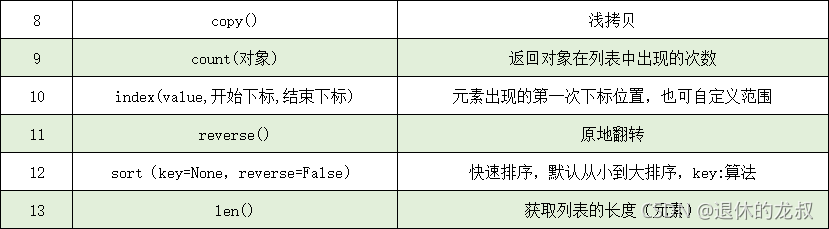
列表 列表是可以存放任何数据,包括整型,浮点型,字符串,布尔型等等,是常用的数据类型之一。 1.列表的创建 列表也是一个可迭代对象 1. 普通形式l [1,2,3,4,5] ---整型列表l ["a","b","c&…...

如何使用工时表管理项目和非项目的资源?
对新机会做出反应的能力是企业竞争优势的关键。项目不断涌现,企业需要了解具体的可用性以及是否有资源来接受新事物。更进一步来说,企业需要知道员工将时间花在哪里。 使用 8Manage工时表解决方案,你将始终拥有做出正确业务决策所需的全面知…...

项目经理如何做好质量保证与标准维持?非技术项目经理如何做好质量管控?
项目经理如何做好质量保证与标准维持?非技术项目经理如何做好质量管控?01.质量保障需要重视哪些执行层面的细节02.非技术出身项目经理如何做好质量保障工作03.质量管理除了PDCA,还有哪些推荐的方法04.质量保证与标准维持,作为常态…...

[文件操作] File 类的用法和 InputStream, OutputStream 的用法
能吃是不是件幸福的事呢 文章目录前言1. 文件的相关定义2. 文件类型3. Java对文件系统的操作3.1 对文件的基础操作3.2 读文件3.3 写文件前言 从这章开始,我们就开始学文件操作相关的知识了~ 1. 文件的相关定义 1.文件的定义可以从狭义和广义两个方面解释. 狭义: 指硬盘上的文…...
索莫菲模型的一些理解 Smomerfeld Model
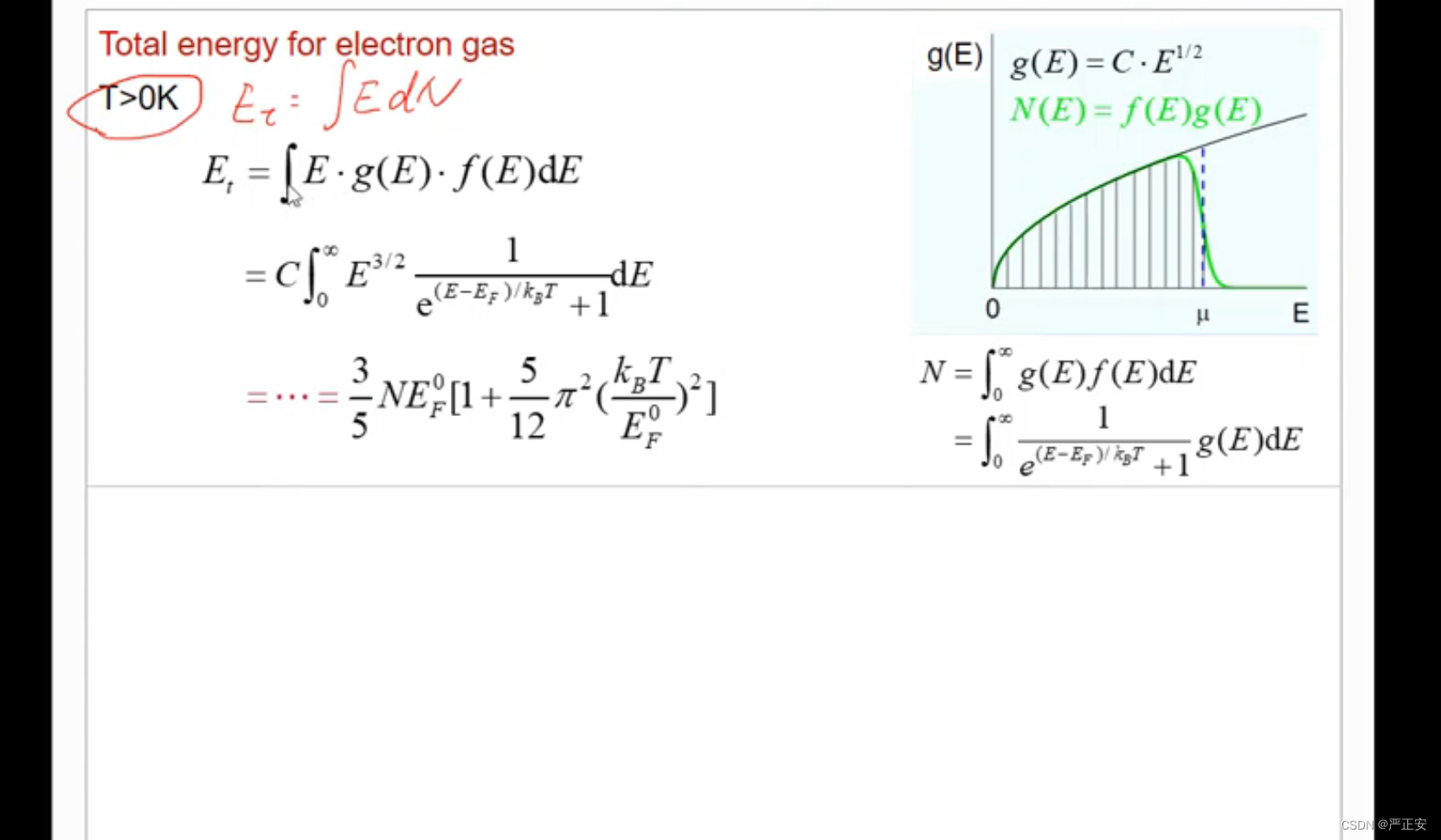
如何解释传统热容算出来的数值与量子模型下的区别? 因为只有费米能附近的电子才能够进行移动,这个是问题的差别所在 我们下面就来介绍如何求费米能(费米能的计算) 既然费米能附近的电子很重要,那么附近的电子有多少很…...
SAP ERP系统MM模块常用增强之四:采购申请输入字段的校验检查
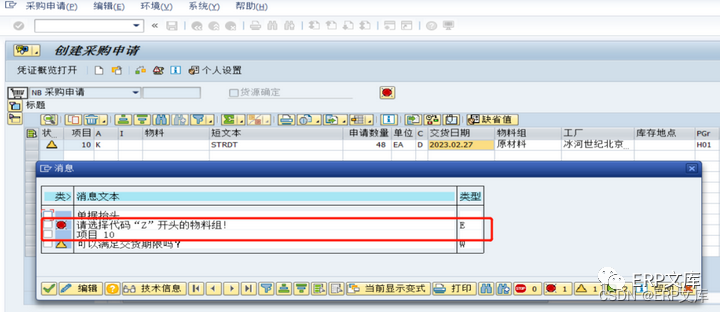
在SAP/ERP项目的实施中采购管理模块(MM)的创建和修改采购申请一般都会有输入字段校验检查的需求,来防止业务人员录入错误或少录入数据,这方面需求部分是可以通过配置实现,比如一些字段是否必输,是否显示等&…...
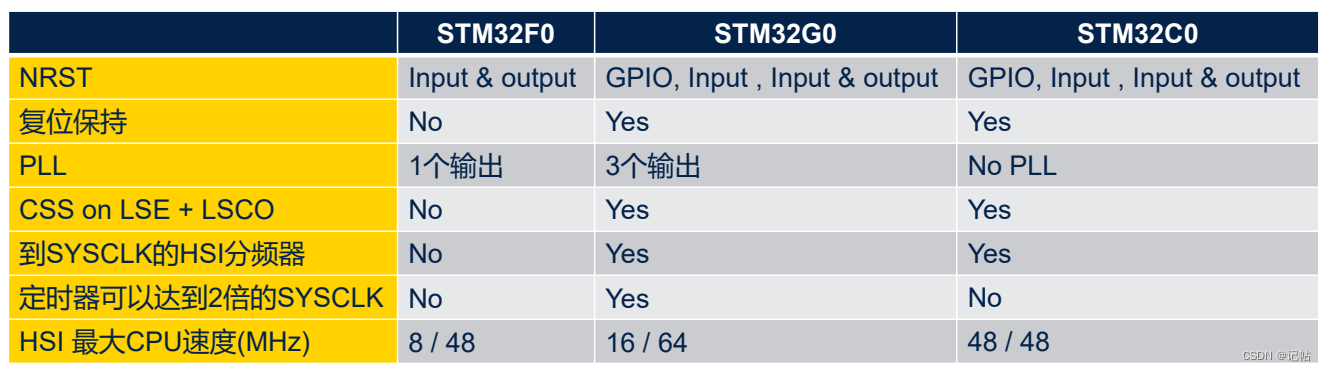
STM32C0介绍(1)----概述
概述 STM32C0系列微控制器是意法半导体公司推出的一款低功耗、高性能的微控制器产品。它们被设计用于需要小型、低功耗和高度可集成的应用程序,如传感器、消费品、电池供电设备、家庭自动化和安全等应用。该系列的微控制器采用ARM Cortex-M0内核,具有丰…...
引导程序开发之一)
windows无盘启动技术开发之传统BIOS(Legacy BIOS)引导程序开发之一
by fanxiushu 2023-03-01 转载或引用请注明原始作者。这个话题可能有点老,UEFI BIOS 已经大量存在,而Legacy BIOS最终会被取代。但是也是作为无盘启动技术里不可或缺的,毕竟还有许多老型号的电脑存在,而且为了兼容性,有…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
