TOP-K问题和向上调整算法和向下调整算法的时间复杂度问题的分析
TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
举个例子:
有十亿个整形数据,我们的内存时4G,也就是102410241024*8个字节的空间,十亿个整形数据需要的是40亿个字节的空间,就占了内存的一半空间,这是不可行的
最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素,将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素
下面我们进行代码的实现:
首先我们生成1000个随机数,范围再十万以内,放入一个数组中:
srand(time(0));
int* a = (int*)malloc(sizeof(int) * 1000);
if (a == NULL)
{perror("malloc");return 0;
}
for (size_t i = 0; i < 1000; i++)
{a[i] = rand() % 100000;
}
然后我们随机将数组中的任意k个元素改为超过十万的数字,方便验证:
a[7] = 100000 + 1;
a[49] = 100000 + 2;
a[123] = 100000 + 3;
a[456] = 100000 + 4;
a[789] = 100000 + 5;
我们还要用到向下调整算法,以便于建堆:
void swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
void AdjustDown(int* a, int n, int parent)
{int child = (parent * 2) + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent=child;child = parent * 2 + 1;}else{break;}}
}
最后我们将a数组中的前k个元素插入到top_k函数的数组里,然后进行一次向下调整算法,将其调整为大堆,然后再用剩下的n-k个元素与堆顶元素进行比较,如果比他大进替换进堆,然后进行向下调整
void top_k(int* a, int n, int k)
{int i = 0;int* top = (int*)malloc(sizeof(int) * k);if (top == NULL){perror("malloc");return;}for (i = 0; i < k; i++){top[i] = a[i];}for (i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(top, k, i);}for (i = k; i < 1000; i++){if (a[i] > top[0]){top[0] = a[i];AdjustDown(top, k, 0);}}
完整代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<assert.h>
void swap(int* p1, int* p2)
{int temp = *p1;*p1 = *p2;*p2 = temp;
}
void AdjustDown(int* a, int n, int parent)
{int child = (parent * 2) + 1;while (child < n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){swap(&a[child], &a[parent]);parent=child;child = parent * 2 + 1;}else{break;}}
}
void top_k(int* a, int n, int k)
{int i = 0;int* top = (int*)malloc(sizeof(int) * k);if (top == NULL){perror("malloc");return;}for (i = 0; i < k; i++){top[i] = a[i];}for (i = (k - 1 - 1) / 2; i >= 0; i--){AdjustDown(top, k, i);}for (i = k; i < 1000; i++){if (a[i] > top[0]){top[0] = a[i];AdjustDown(top, k, 0);}}for (i = 0; i < k; i++){printf("%d ", top[i]);}free(top);
}
int main()
{srand(time(0));int* a = (int*)malloc(sizeof(int) * 1000);if (a == NULL){perror("malloc");return 0;}for (size_t i = 0; i < 1000; i++){a[i] = rand() % 100000;}a[7] = 100000 + 1;a[49] = 100000 + 2;a[123] = 100000 + 3;a[456] = 100000 + 4;a[789] = 100000 + 5;int k = 5;top_k(a, 1000, k);
}
向上调整算法和向下调整算法的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):

我们令高度为h,节点个数n就等于2^(h)-1个
那么在向上调整算法中:
最坏情况下,最后一层的节点需要向上移动h-1次,依次类推,就得到总次数的表达式,然后再用错位相减法和n和h的关系就能求出时间复杂度f(n)了
在向下调整算法中:
最坏情况下,倒数第二层节点向下只移动一次,第一层最多移动h-1次
总结下来我们就会发现,向上调整算法中是多节点乘多层数的关系,而向下调整算法则是多节点乘少层数的关系,我们进行比较就会发现其实向下调整算法的效率更高,所以在平常的排序和建堆中我们 最常用的还是向下调整算法
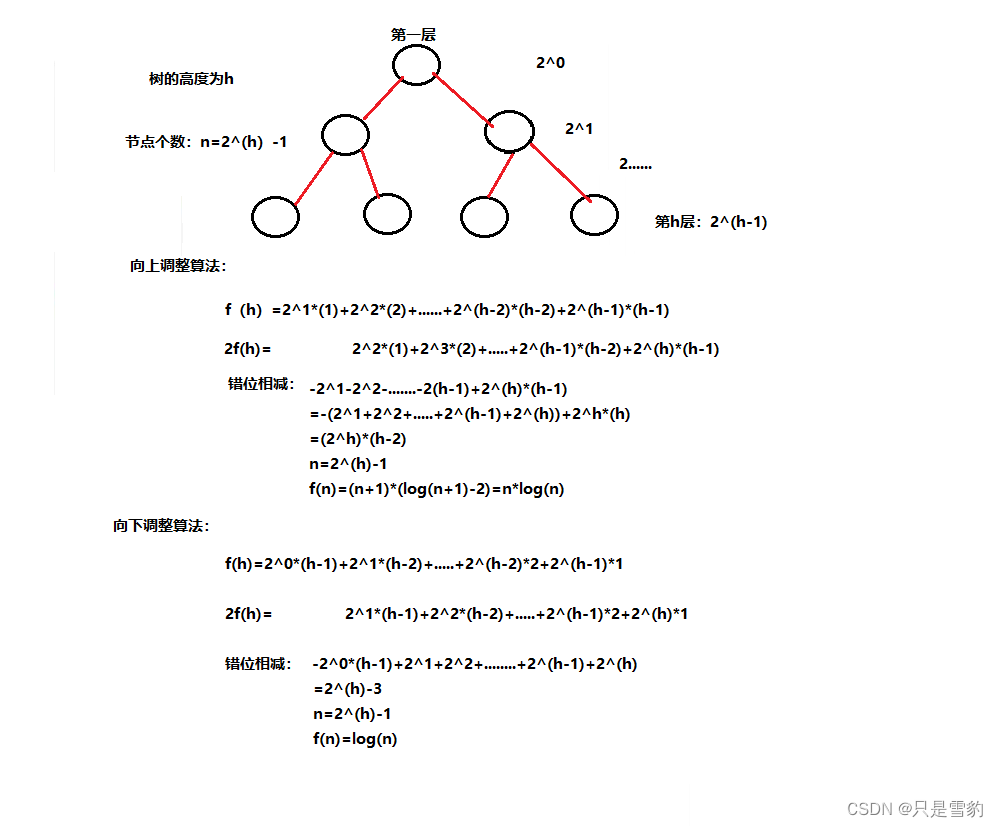
向上调整算法的时间复杂度为:
n*log(n)
向下调整算法的时间复杂度为:
log(n)
因此,向下调整算法的效率是远大于向上调整算法的!
好了,今天的分享到这里就结束了,谢谢大家的支持!
相关文章:

TOP-K问题和向上调整算法和向下调整算法的时间复杂度问题的分析
TOP-K问题 TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等 对于Top-K问题,能想到的最简单直接的方式就是排序,但是…...

3、服务器性能剖析
性能优化简介 **我们将性能定义为完成某件任务所需要的时间度量,换句话说,性能即响应时间,这是一个非常重要的原则。**我们通过任务和时间而不是资源来测量性能。数据库服务器的目的是执行sql语句,所以他关注的任务是查询或者语句…...

xxl-job 分布式任务调度框架
文章目录 分布式任务调度XXL-Job 简介XXL-Job 环境搭建XXL-Job (源码说明)配置部署调度中心docker安装 Bean模式任务(方法形式)-入门案例任务详解任务详解-执行器任务详解-基础配置任务详解-调度配置任务详解-基础配置任务详解-阻塞处理策略任务详解-路由策略 路由策略路由策略…...

软件使用-stm32入门
这节主要是介绍大家使用两个软件。这两个软件也是比较常用的,里面也有很多有意思的功能,可以给大家介绍一下。 1. FlyMcu 软件 这个软件可以通过串口给 STM32 下载程序,如果你没有 STLINK,就可以用这个软件通过串口下载程序。 …...
使用MAT分析内存泄漏(mac)
前言 今天主要简单分享下Eclipse的Memory Analyzer在mac下的使用。 一、Mat(简称)干什么的? 就是分析java内存泄漏的工具。 二、使用步骤 1.下载 mac版的现在也分芯片,别下错了。我这里是M2芯片的,下载的Arch64的。 …...
【Vue】Linux 运行 npm run serve 报错 vue-cli-service: Permission denied
问题描述 在Linux系统上运行npm run serve命令时,控制台报错: sudo npm run serve project50.1.0 serve vue-cli-service serve sh: 1: vue-cli-service: Permission denied错误截图如下: 原因分析 该错误是由于vue-cli-service文件权限不…...
LeetCode的几道题
一、捡石头 292 思路就是: 谁面对4块石头的时候,谁就输(因为每次就是1-3块石头,如果剩下4块石头,你怎么拿,我都能把剩下的拿走,所以你就要想尽办法让对面面对4块石头的倍数, 比如有…...

NLP/Natural Language Processing
一、NLP是什么 自然语言处理( Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向,也就是人们常说的「自然语言处理」,就是研究如何让计算机读懂人类语言,即将人的自然语言转换为计算机可以阅读的指令。它研…...
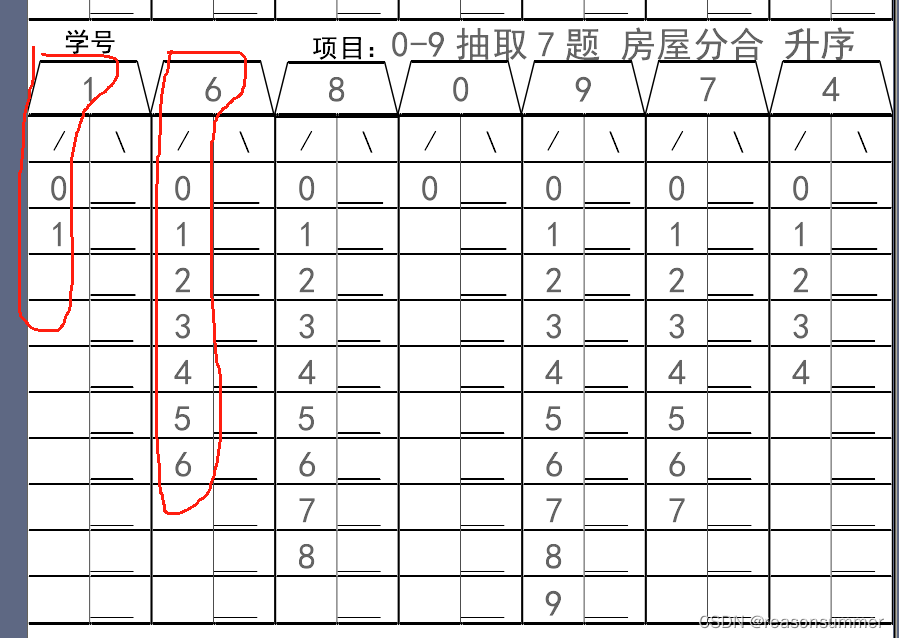
【教学类-06-12】20231202 0-9数字分合-房屋样式(一)-下右空-升序-抽7题
作品展示-屋顶分合(0-9之间随机抽取7个不重复分合) 背景需求: 大班幼儿学分合题,通常区角里会设计一个“房屋分合”的样式 根据这种房屋样式,设计0-9内的升序分合题模板 素材准备 WORD样式 代码展示: 2-9…...
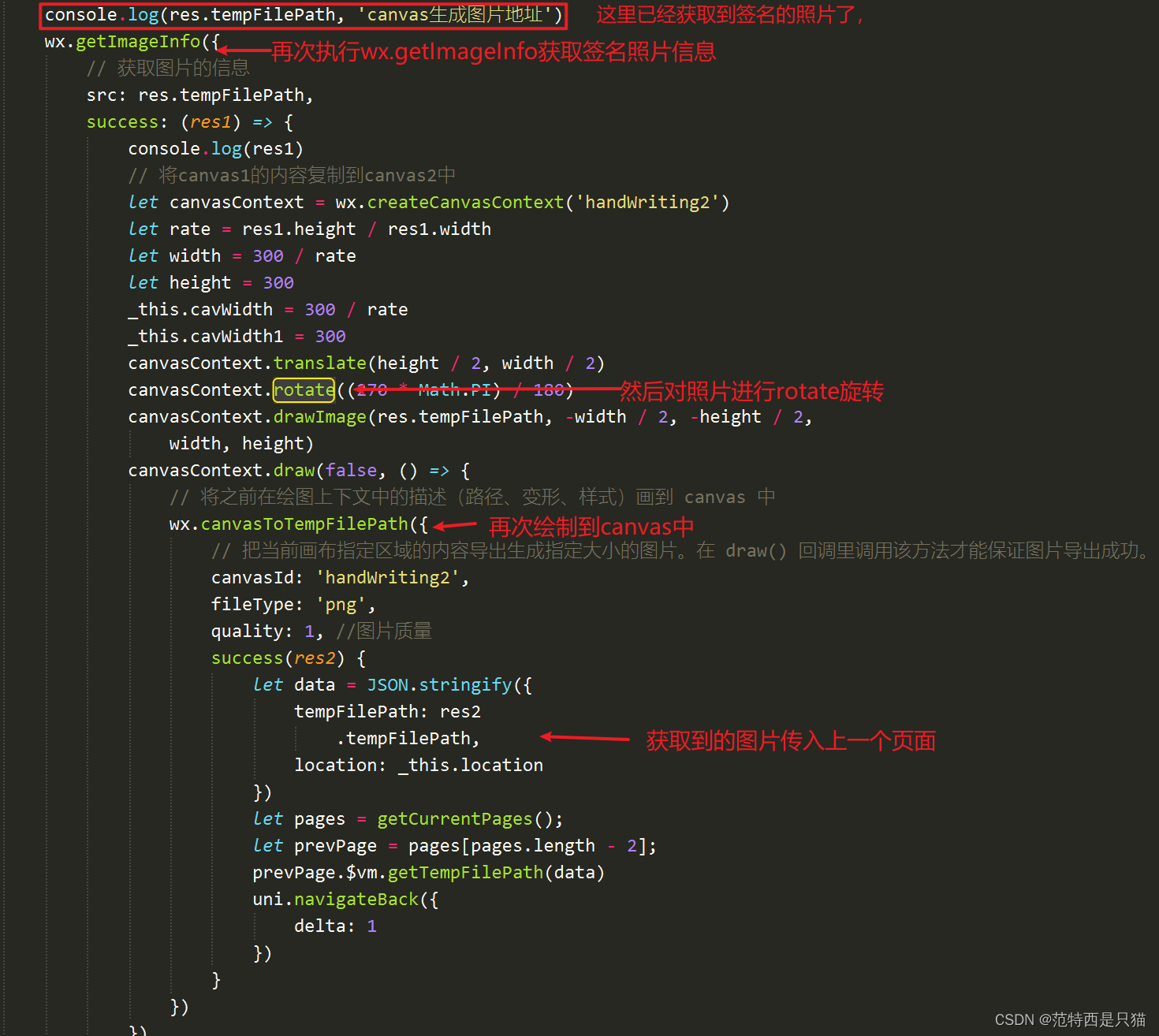
uni-app 微信小程序 电子签名及签名图片翻转显示功能
文章目录 1. 需求背景2. 开始撸2.1 点击 重写 进入签名页面(上图一)2.2 书写签名,点击确认返回,及图片翻转显示(上图二,三) 3. 图片进行翻转,返回翻转后的图片 1. 需求背景 接的一个…...

MySQL 8.0关键字和保留字
官网地址: https://dev.mysql.com/doc/refman/8.0/en/keywords.html 可以粘贴出去自己排版整理 {accessible} {account} {action} {active} {add} {admin} {after} {against} {aggregate} {algorithm} {all} {alter} {always} {analyse} {analyze} …...

PyLMKit(3):基于角色扮演的应用案例
角色扮演应用案例RolePlay 0.项目信息 日期: 2023-12-2作者:小知课题: 通过设置角色模板并结合在线搜索、记忆和知识库功能,实现典型的对话应用功能。这个功能是大模型应用的基础功能,在后续其它RAG等功能中都会用到这个功能。功…...

JAVA全栈开发 集合详解(day14+day15汇总)
一、数组 数组是一个容器,可以存入相同类型的多个数据元素。 数组局限性: 长度固定:(添加–扩容, 删除-缩容) 类型是一致的 对象数组 : int[] arr new int[5]; … Student[] arr …...
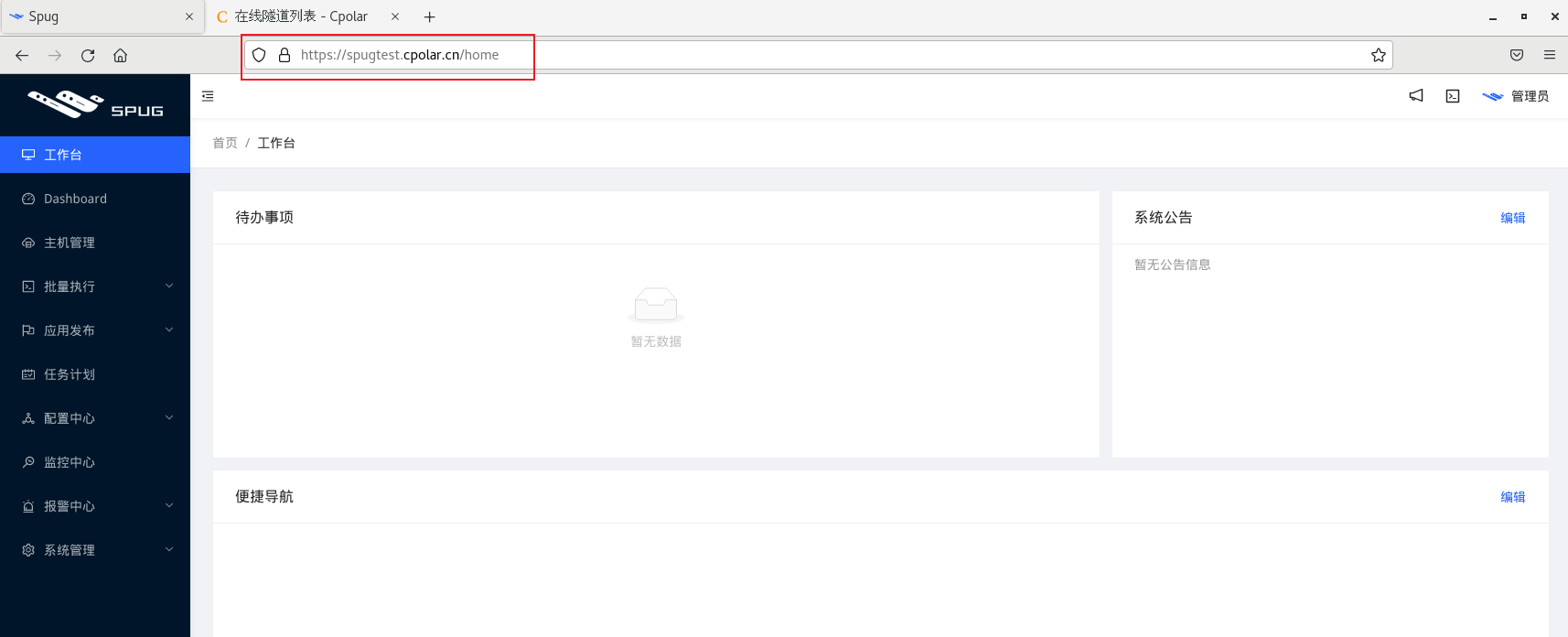
Linux Spug自动化运维平台本地部署与公网远程访问
文章目录 前言1. Docker安装Spug2 . 本地访问测试3. Linux 安装cpolar4. 配置Spug公网访问地址5. 公网远程访问Spug管理界面6. 固定Spug公网地址 前言 Spug 面向中小型企业设计的轻量级无 Agent 的自动化运维平台,整合了主机管理、主机批量执行、主机在线终端、文件…...

zookeeper集群和kafka集群
(一)kafka 1、kafka3.0之前依赖于zookeeper 2、kafka3.0之后不依赖zookeeper,元数据由kafka节点自己管理 (二)zookeeper 1、zookeeper是一个开源的、分布式的架构,提供协调服务(Apache项目&…...
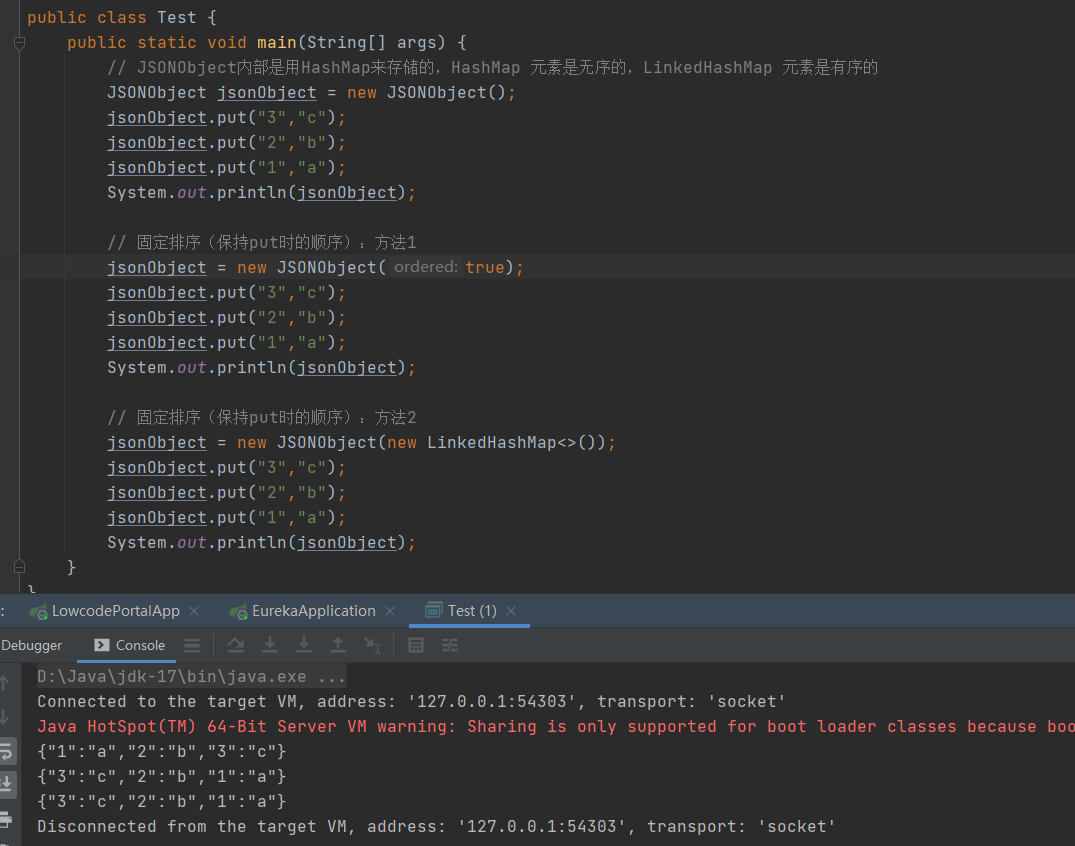
Java——》JSONObjet 数据顺序
推荐链接: 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

【个人记录】NGINX反向代理grpc服务
最开始使用proxy_pass去代理了grpc服务,结果请求时候报错提示: rpc error: code Unavailable desc connection error: desc "error reading server preface: http2: frame too large"后来才知道代理grpc服务需要使用grpc_pass,…...

【小白推荐】安装OpenCV4.8 系统 Ubuntu 22.04LST Linux.
先看一下目录,知道大致的流程! 文章目录 安装OpenCV安装依赖下载源码配置与构建安装 测试编写CMakeListx.txt编写测试代码 安装OpenCV 安装依赖 sudo apt update && sudo apt upgrade sudo apt install cmake ninja-build build-essential lib…...
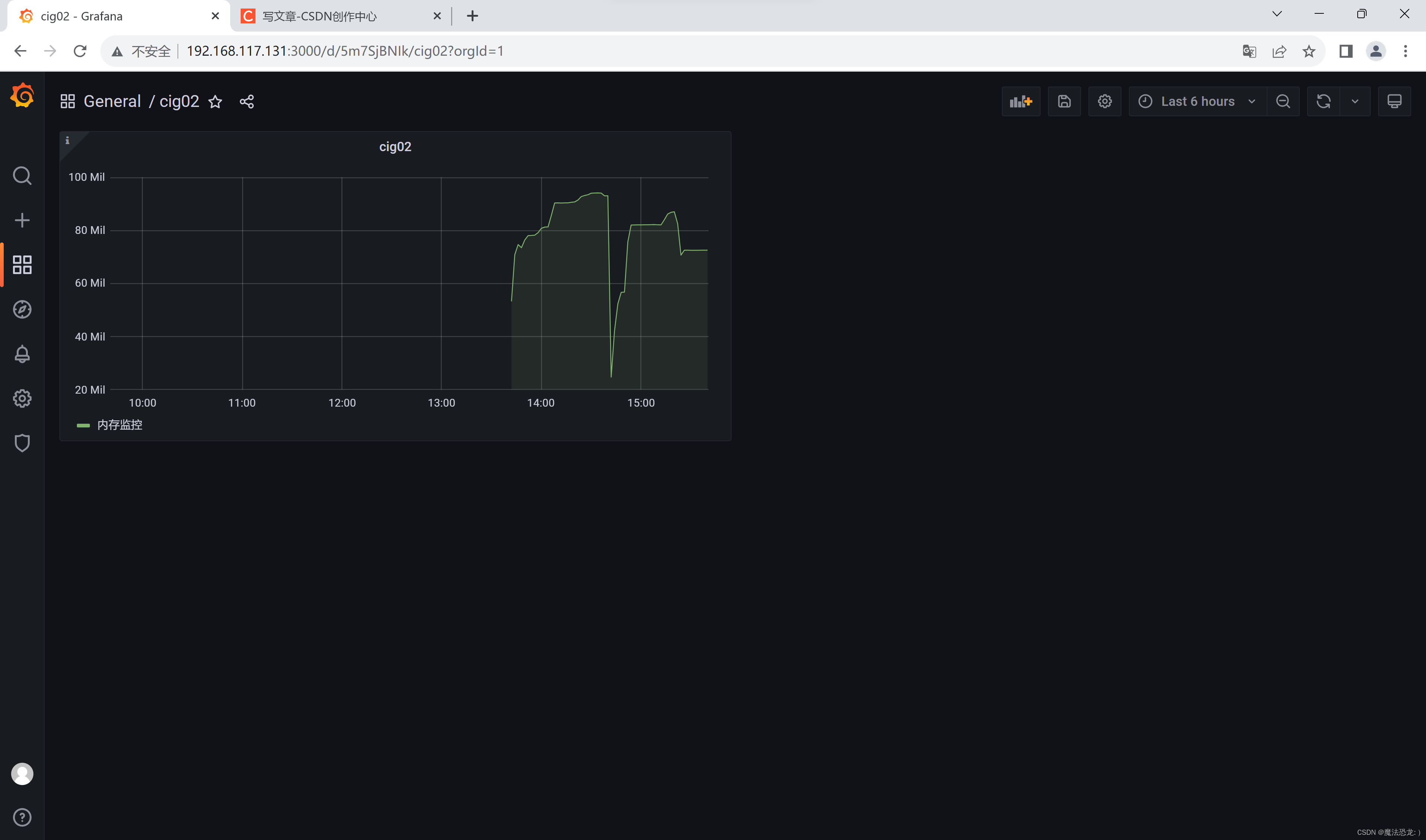
使用Docker Compose搭建CIG监控平台
CIG简介 CIG监控平台是基于CAdvisor、InfluxDB和Granfana构建的一个容器重量级监控系统,用于监控容器的各项性能指标。其中,CAdvisor是一个容器资源监控工具,用于监控容器的内存、CPU、网络IO和磁盘IO等。InfluxDB是一个开源的分布式时序、时…...

前端文本省略号后面添加复制文字
前端文本省略号后面添加复制文字 1、效果图 2、代码展示 <div class"link-content-wrap" click"copyLinkText"><div class"link-content">{{ shareResult.url || }} </div><span class"show-ellipsis" click&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...
