Programming Contest 2023(AtCoder Beginner Contest 331)D题 Tile Pattern --- 题解
目录
D - Tile Pattern
题目大意:
思路:
代码:
D - Tile Pattern
D - Tile Pattern (atcoder.jp)
题目大意:
给你一个n和q,n为局部棋盘大小(n*n) 并且给出局部棋盘中黑白子位置的放置情况,q为查询次数,然后使用局部棋盘填充整个棋盘,全局棋盘大小为(10^9 * 10^9),然后一次查询会给出a b c d,(a,b)表示选中棋盘的左上角,(c,d)表示选中棋盘的右上角,然后问在这个选中区域中有多少个黑色棋子。
思路:
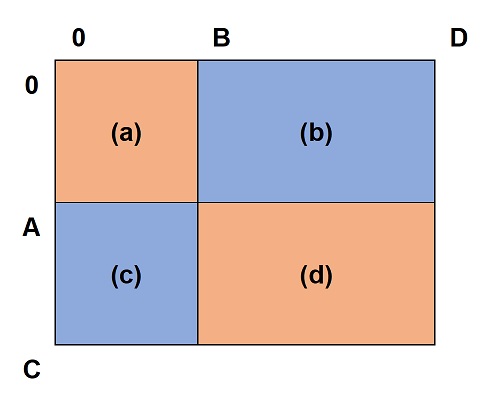
我们其实可以通过预处理这个局部棋盘矩阵,得到任意以(0,0)为左上角的矩阵的含有黑色棋子的个数,即dp[i][j]表示 (0,0) -> (i,j)的矩阵含有黑色棋子的个数。
如果把这个选中矩阵填充成 (0,0) -> (c,d). 那么答案就为 dp[c][d] - dp[c][b-1] - dp[a-1][d] + dp[a-1][b-1].
但是如果a b c d 都大于n,那么其实我们可以沿着这个思路,将d区看作是完整的m*n个局部棋盘,c区看作是列不全的m个局部棋盘,b区看作是行不全的n个局部棋盘,a区看作是列不全和行不全的棋盘,然后d区可以直接通过 m*m*dp[n][n]求得,c区和b区都分别等于m个列不全和行不全的局部棋盘和n个列不全和行不全的局部棋盘,然后这些局部棋盘又可以通过 dp[c][d] - dp[c][b-1] - dp[a-1][d] + dp[a-1][b-1]得到。
代码:
import java.io.*;
import java.math.BigInteger;
import java.util.StringTokenizer;/*** @ProjectName: study3* @FileName: Ex37* @author:HWJ* @Data: 2023/12/2 20:50*/
public class Ex37 {static long[][] dp;static int n;public static void main(String[] args) {n = input.nextInt();int q = input.nextInt();long[][] map = new long[n][n];dp = new long[n + 1][n + 1];for (int i = 0; i < n; i++) {String str = input.next();char[] s = str.toCharArray();for (int j = 0; j < n; j++) {if (s[j] == 'B') {map[i][j] = 1;}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + map[i - 1][j - 1];}}for (int i = 0; i < q; i++) {int a = input.nextInt();int b = input.nextInt();int c = input.nextInt();int d = input.nextInt();long ans = f(a, b, c+1, d+1);out.println(ans);}out.flush();out.close();}public static long f(int a, int b, int c, int d){return g(c,d) - g(c,b) - g(a,d) + g(a,b);}public static long g(int a, int b){if (a <= n && b <= n) return dp[a][b];int Hq = a / n, Hr = a % n;int Wq = b / n, Wr = b % n;long ret = 0;ret += g(n, n) * Hq * Wq;ret += g(Hr, n) * Wq;ret += g(n, Wr) * Hq;ret += g(Hr, Wr);return ret;}static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static Input input = new Input(System.in);static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static class Input {public BufferedReader reader;public StringTokenizer tokenizer;public Input(InputStream stream) {reader = new BufferedReader(new InputStreamReader(stream), 32768);tokenizer = null;}public String next() {while (tokenizer == null || !tokenizer.hasMoreTokens()) {try {tokenizer = new StringTokenizer(reader.readLine());} catch (IOException e) {throw new RuntimeException(e);}}return tokenizer.nextToken();}public String nextLine() {String str = null;try {str = reader.readLine();} catch (IOException e) {// TODO 自动生成的 catch 块e.printStackTrace();}return str;}public int nextInt() {return Integer.parseInt(next());}public long nextLong() {return Long.parseLong(next());}public Double nextDouble() {return Double.parseDouble(next());}public BigInteger nextBigInteger() {return new BigInteger(next());}}
}
/*
10 1
BBBWWWBBBW
WWWWWBBBWB
BBBWBBWBBB
BBBWWBWWWW
WWWWBWBWBW
WBBWBWBBBB
WWBBBWWBWB
WBWBWWBBBB
WBWBWBBWWW
WWWBWWBWWB
5 21 21 93*/
相关文章:

Programming Contest 2023(AtCoder Beginner Contest 331)D题 Tile Pattern --- 题解
目录 D - Tile Pattern 题目大意: 思路: 代码: D - Tile Pattern D - Tile Pattern (atcoder.jp) 题目大意: 给你一个n和q,n为局部棋盘大小(n*n) 并且给出局部棋盘中黑白子位置的放置情况,q为查询次数…...

Google测试框架googletest简介与使用方法
环境准备(Ubuntu) 下载 git clone https://github.com/google/googletest.git 安装 cd googletest // 创建build目录 mkdir build cd build //编译安装 cmake .. make sudo make install 检查是否安装成功 ls /usr/local/lib// 存在以下文件则说明…...

进程的创建:fork()
引入 创建进程的方式我们已经学习了一个!在我们运行指令(或者运行我们自己写的可执行程序)的时候不就是创建了一个进程嘛?那个创建进程的方式称为指令级别的创建子进程! 那如果我们想要在代码中创建进程该怎么办呢? fork() for…...

Fabric:创建应用通道
搭建自定义网络可以参考文章: https://blog.csdn.net/yeshang_lady/article/details/134113296 1 创建通道 网络搭建完成之后,就可以开始创建通道了。Fabric V2.5.4中可以在不创建系统通道的情况下直接创建应用通道。 1.1 修改配置文件 先创建配置文…...
力扣每日一题(2023-11-30)
力扣每日一题 题目:1657. 确定两个字符串是否接近 日期:2023-11-30 用时:21 m 07 s 时间:11ms 内存:43.70MB 代码: class Solution {public boolean closeStrings(String word1, String word2) {if(word1.…...
内部类Lambda
静态内部类 /*** 静态成员是在类加载成字节码时就已经存在的,静态只能访问静态*/ public class Demo {public static void main(String[] args) {Outer.Inner.show();} }class Outer {int num1 10;static int num2 20;static class Inner {static void show() {Outer outer …...

设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A[1...n]和 Bfl...n]中,试编写算法建立该二叉树的二叉链表。
题目描述:设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A[1…n]和 B[1…n]中,试编写算法建立该二叉树的二叉链表。 分析: 对于一颗二叉树,知道其中序和先序序列就可以完全确定…...

什么是Daily Scrum?
Daily Scrum(每日站会),Scrum Master要确保这个会在每天都会开。这个会的目的就是检查正在做的东西和方式是否有利于完成Sprint目的,并及时做出必要的调整。 每日站会一般只开15分钟,为了让事情更简单些,这…...

逆波兰表达式求值[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个字符串数组tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。 有效的算符为 ‘’、‘-’、‘*’ 和 ‘/’ 。 每个操作数(运算对象)都…...

Oracle连接和使用
5. Oracle连接和使用 5.1. sqlplus sqlplus作为甲骨文公司提供的一款本族工具产品,有着悠久的历史和积淀,它几乎伴随着Oracle数据库产生至今的整个生命周期,而且,还会继续和Oracle数据库产品相伴一直发展下去。该工具看似简单灵活的背后,却为广大用户使用Oracle数据库提…...

redis单线程为什么这么快
redis单线程为什么这么快 redis是使用的单线程来进行操作的,因为所有的数据都是在内存中的,内存操作特别快。而且单线程避免了多线程切换性能损耗问题 单线程如何处理并发客户端连接? redis利用epoll来实现IO多路复用,将连接信息和…...
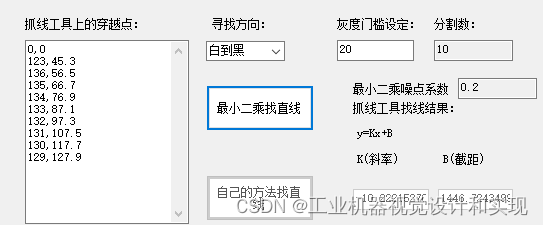
工业机器视觉megauging(向光有光)使用说明书(五,轻量级的visionpro)
这个说明主要介绍抓线功能。 第一步,添加线工具,鼠标双击工具箱“抓线”,出现如下界面: 第二步,我们拉一条,“九点标定”到“抓线1”的线,和visionpro操作一样: 第三步,…...

【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
文章目录 【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛A.星期几考试?C.信件D、乘除法E、不知道叫什么名字F.我要学会盾反!G.闪闪发光心动不已!H.不想想背景的gcdI.uu爱玩飞行棋J.火柴人小游戏K .有趣的BOSS 【LittleXi】2023年广东…...

【C语言:数据在内存中的存储】
文章目录 1.整数在内存中的存储1.1整数在内存中的存储1.2整型提升 2.大小端字节序2.1什么是大小端2.2为什么有大小端之分 3.整数在内存中的存储相关题目题目一题目二题目三题目四题目五题目六题目七 4.浮点数在内存中的存储4.1浮点数存的过程4.2浮点数取得过程 在这之前呢&…...

每日一练:阿姆斯特朗数
如果一个 n 位正整数等于其各位数字的 n 次方之和,则称该数为阿姆斯特朗数。 例如 1^3 5^3 3^3 153。 1000 以内的阿姆斯特朗数: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407。...
)
fatal: remote error: upload-pack: not our ref (未解决问题)
PX4使用 git submodule update --init --recursive报错 fatal: remote error: upload-pack: not our ref解决办法参考:https://stackoverflow.com/questions/61163082/why-does-git-submodule-update-fail-with-fatal-remote-error-upload-pack-not-o 感觉就是清…...
、readline()、readlines() 函数 读取文件)
Python 3 使用 read()、readline()、readlines() 函数 读取文件
1 样例文件 example.txt 春晓 孟浩然〔唐代〕 春眠不觉晓,处处闻啼鸟。 夜来风雨声,花落知多少。 2 分别使用 read()、readline()、readlines() 函数 2.1 # read() -------- 一次性读取所有文本,以字符串的形式返回结果。 # read() ----…...
勒索解密后oracle无法启动故障处理----惜分飞
客户linux平台被勒索病毒加密,其中有oracle数据库.客户联系黑客进行解密【勒索解密oracle失败】,但是数据库无法正常启动,dbv检查数据库文件报错 [oraclehisdb ~]$ dbv filesystem01.dbf DBVERIFY: Release 11.2.0.1.0 - Production on 星期一 11月 27 21:49:17 2023 Copyrig…...
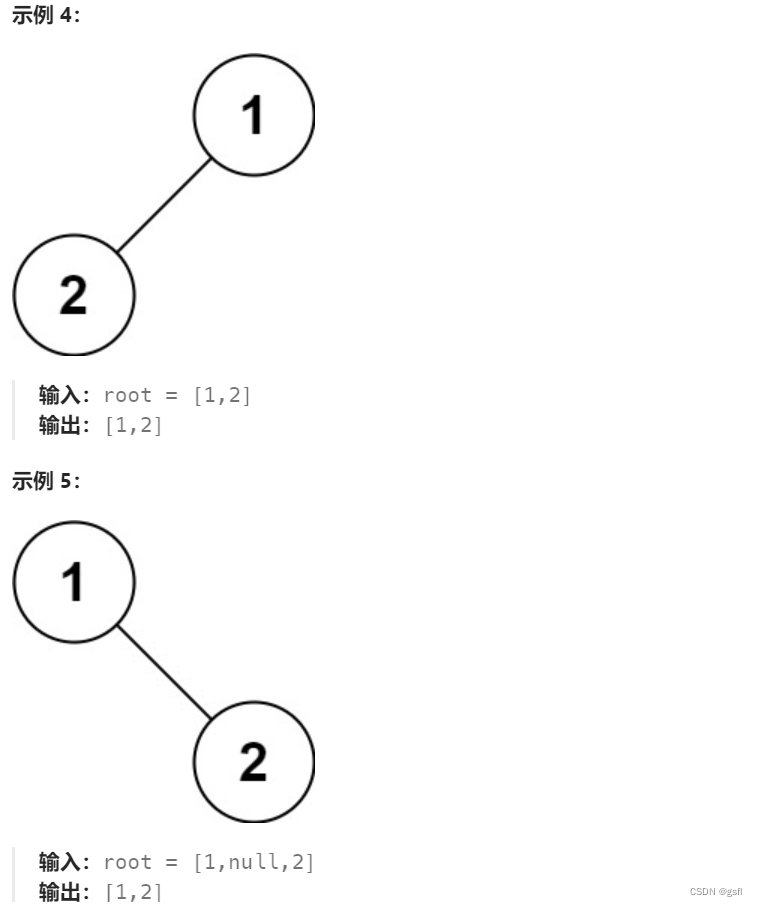
Leetcode144. 二叉树的前序遍历-C语言
文章目录 题目介绍题目分析解题思路1.创建一个数组来储存二叉树节点的值2.根据二叉树的大小来开辟数组的大小3.边前序遍历边向创建的数组中存入二叉树节点的值 完整代码 题目介绍 题目分析 题目要求我们输出二叉树按前序遍历排列的每个节点的值。 解题思路 1.创建一个数组来…...

dmesg命令在软件测试中的实际应用
简介:当你想要了解 Linux 系统在启动时究竟发生了什么?或者当硬件设备不工作时,如何进行调试?这就是 dmesg 命令的用武之地。本文将介绍 dmesg 的基本功能,并深入探讨其在软件测试中的实际应用。 历史攻略:…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
