【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
文章目录
- 【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
- A.星期几考试?
- C.信件
- D、乘除法
- E、不知道叫什么名字
- F.我要学会盾反!
- G.闪闪发光心动不已!
- H.不想想背景的gcd
- I.uu爱玩飞行棋
- J.火柴人小游戏
- K .有趣的BOSS
【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
[赛题链接](2023年广东工业大学腾讯杯新生程序设计竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ (nowcoder.com))
A.星期几考试?
签到题,全部加起来 m o d 7 mod7 mod7就好啦
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){int n,m;cin>>n>>m;map<int,int> mp;int time = 0;int ac=0;for(int i=0;i<m;i++){int tp;string cond;cin>>tp>>cond;if(mp[tp]==-1) continue;if(cond=="AC"&&mp[tp]!=-1){time+=mp[tp];mp[tp] = -1;ac++;}elsemp[tp]++;}cout<<ac<<" "<<time<<endl;
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;while(t--){solve();}
}
C.信件
脑经急转弯
小心爆int
不难发现,每个括号里的数字都是奇数,然后如果出现了5,5乘上任意的奇数,末尾都是5
然后发现,n等于2的时候出现了5
所以可以分类讨论如下:
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){ll n ;cin>>n;if(n==2ll)cout<<5<<endl;elsecout<<9<<endl;
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;cin>>t;while(t--){solve();}
}
D、乘除法
数学
可以发现5和6互斥
把x看成一堆素数的乘积,
那么x中出现的6要大于y中出现的6
x中出现的5要小于y中出现的5
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){ll x,y;cin>>x>>y;ll ans =0 ;ll cnt1=0,cnt2=0;ll xx = x,yy=y;while(xx%6==0) xx/=6,cnt1++;while(yy%6==0) yy/=6,cnt2++;if(cnt1<cnt2) {cout<<-1<<endl;return;}for(ll i=0;i<cnt1-cnt2;i++){x/=6;ans++;}while(x<y){x*=5;ans++;}if(x==y)cout<<ans<<endl;elsecout<<-1<<endl;
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);ll t = 1;cin>>t;while(t--){solve();}
}
E、不知道叫什么名字
前缀和+map
可以把男生看成1,女生看成-1
那么就是,求一个区间,使得区间和为0
可以考虑前缀和做法,枚举到 p r e [ i ] pre[i] pre[i]的时候,去查找最左边等于 p r e [ i ] pre[i] pre[i]的值,不妨记作pre[j],那么因为 p r e [ i ] = = p r e [ j ] pre[i]==pre[j] pre[i]==pre[j],所以 p r e [ i ] − p r e [ j ] = 0 pre[i]-pre[j]=0 pre[i]−pre[j]=0,区间长度就是 i − j i-j i−j
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){int n;cin>>n;vector<int> a(n);for(int &x:a)cin>>x;vector<int> pre(n,a[0]?1:-1);for(int i=1;i<n;i++)pre[i] = pre[i-1]+(a[i]?1:-1);map<int,int> mp;mp[0] = -1;for(int i=0;i<n;i++){if(mp.find(pre[i])!=mp.end())continue;mp[pre[i]] = i;}int ans = 0;for(int i=0;i<n;i++){int x = pre[i];ans =max(ans,i-mp[x]);}cout<<ans<<endl;
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;while(t--){solve();}
}
F.我要学会盾反!
盾之勇者成名录
dp+数学+同余类划分
可以先排序,然后可以发现x,x+1,x+2,x+3这样连着的值可以连续地被消除,然后x+4的时候就陷入了冷却,那么什么时候解除冷却呢,当然是在x+4+p*v的点上可以解除冷却
如何快速找到符合条件的x+4+p*v这个点,我们可以发现x+4和x+4+p * v同余,所以可以用map记录这个同余类,找到后面的那个点之后,直接取那个点往后走的最大值,类似于dp
遍历的时候可以从大往小遍历
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){ll n,v;cin>>n>>v;vector<ll> a(n);for(ll&x:a)cin>>x;sort(a.begin(),a.end());vector<vector<ll>> vb;vector<ll> b = {a[0]};for(ll i=1;i<n;i++){if(b.size()==0||a[i]-b.back()<=1){b.push_back(a[i]);}else{vb.push_back(b);b = {a[i]};}}vb.push_back(b);map<ll,ll> mp;ll di = 0;for(ll i=vb.size()-1;i>=0;i--){auto b = vb[i];ll r = b.back()+1;ll w = mp[r%v];for(ll j=b.size()-1;j>=0;j--){w++;mp[b[j]%v] = w;di = max(di,w);}}cout<<n-di<<endl;
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);ll t = 1;cin>>t;while(t--){solve();}
}G.闪闪发光心动不已!
dp
题目感觉表述不是很清晰qwq
翻译:一个最长子串,使得出现若干个"kira"之后出现若干个"doki"
可以考虑先从前往后dp,求出每个位置前面有多少个kira,然后从后往前do,求出多少个doki,然后拼接起来就行啦
dp的时候可以自己设置一下状态
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"// kirakirakira...dokidokidoki
//状态机dp1
void solve(){int n;cin>>n;string s;cin>>s;vector<pair<int,int>> dp1(n);string t = "kira";dp1[0] = {0,0};if(s[0] == 'k')dp1[0] = {0,1};for(int i=1;i<n;i++){dp1[i] = dp1[i-1];if(t[dp1[i-1].second]==s[i]){if(s[i] == 'a'){dp1[i].first+=1;dp1[i].second = 0;}else{dp1[i].second = dp1[i-1].second+1;}}}vector<pair<int,int>> dp2(n);t = "ikod";dp2[n-1] = {0,0};if(s[n-1] == 'i')dp2[n-1] = {0,1};for(int i=n-2;i>=0;i--){dp2[i] = dp2[i+1];if(t[dp2[i+1].second]==s[i]){if(s[i] == 'd'){dp2[i].first+=1;dp2[i].second = 0;}else{dp2[i].second = dp2[i+1].second+1;}}}int ans =0 ;for(int i=0;i<n-1;i++){if(dp1[i].first&&dp2[i+1].first){ans=max(ans,dp1[i].first*4+dp2[i+1].first*4);}}cout<<ans<<endl;
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;while(t--){solve();}
}
H.不想想背景的gcd
数学
挺有意思的,现学了一下辗转相减法
// while (a != b) {
// if (a > b)
// a = a - b;
// else
// b = b - a;
// }
先把a数组倒序排序
g c d ( a 1 + b j + c k , a 2 + b j + c k , . . . , a n − 2 + b j + c k , a n − 1 + b j + c k ) gcd(a_1+b_j+c_k,a_2+b_j+c_k,...,a_n-2+b_j+c_k,a_n-1+b_j+c_k) gcd(a1+bj+ck,a2+bj+ck,...,an−2+bj+ck,an−1+bj+ck)
等价于
g c d ( a 1 − a 2 , a 2 − a 3 , . . . , a n − 2 − a n − 1 , a n − 1 + b j + c k ) gcd(a_1-a_2,a_2-a_3,...,a_n-2-a_n-1,a_n-1+b_j+c_k) gcd(a1−a2,a2−a3,...,an−2−an−1,an−1+bj+ck)
因为根据辗转相减法,$gcd(a_1+p,a_2+p) $= g c d ( a 1 − a 2 , a 2 + p ) gcd(a_1-a_2,a_2+p) gcd(a1−a2,a2+p)
由gcd的结合律,我们可以对每项都使用这个技巧,就化完了
对于上面式子,再次由gcd结合律,可以得到
g c d ( a 1 − a 2 , a 2 − a 3 , . . . , a n − 2 − a n − 1 , a n − 1 + b j + c k ) gcd(a_1-a_2,a_2-a_3,...,a_n-2-a_n-1,a_n-1+b_j+c_k) gcd(a1−a2,a2−a3,...,an−2−an−1,an−1+bj+ck) = g c d ( g c d ( a 1 − a 2 , a 2 − a 3 , . . . , a n − 2 − a n − 1 ) , a n − 1 + b j + c k ) gcd(gcd(a_1-a_2,a_2-a_3,...,a_n-2-a_n-1),a_n-1+b_j+c_k) gcd(gcd(a1−a2,a2−a3,...,an−2−an−1),an−1+bj+ck)
前面n-1项可以预处理出来,后面b,c可以直接枚举
小心卡常
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"inline ll gcd(ll x, ll y) {return y == 0 ? x : gcd(y, x % y);
}void solve(){ll n;cin>>n;vector<ll> a(n),b(n),c(n);for(ll &x:a) cin>>x;for(ll &x:b) cin>>x;for(ll &x:c) cin>>x;ll g = 0;sort(a.begin(),a.end());reverse(a.begin(),a.end());for(ll i=0;i<n-1;i++){g= gcd(g,a[i]-a[i+1]);}ll an_1 = a[n-1];ll mx = 0,mi = 2e18;for(ll i=0;i<n;i++){for(ll j=0;j<n;j++){ll ng = gcd(g,an_1+b[i]+c[j]);mx =max(mx,ng);mi = min(mi,ng);}} cout<<mi<<" "<<mx<<endl;
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);ll t = 1;while(t--){solve();}
}
I.uu爱玩飞行棋
背包dp
非常经典的背包,可以发现距离只有1000
维护一个长度为1010的背包,dp[i]表示到达这个位置花费的最少的骰子🎲
然后枚举骰子,从左往右维护每个点
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){int n,m;cin>>n>>m;vector<int> a(m);for(int&x:a)cin>>x;vector<int> dp(n+10,2*m);dp[9] = 0;int tar = 10+n-1;for(int i=0;i<m;i++){auto tdp = dp;for(int j=0;j<tar;j++){int to = j + a[i];if(to > tar){to = tar-(to-tar);}tdp[to] = min(tdp[to],dp[j]+1);}dp = tdp;}if(dp[tar]==2*m){cout<<-1<<endl;}elsecout<<dp[tar];
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;while(t--){solve();}
}
J.火柴人小游戏
贪心+优先队列
(很多同学直接二分+check,但是我没想出来 O ( n m ) O(nm) O(nm)的check,这样复杂度就是 O ( n m l g 2 ( n m ) ) O(nmlg^2(nm)) O(nmlg2(nm))了,导致TLE
我没可以直接bfs,当从优先队列中取出来的点大于了当前的能量值,我们就我们我们自己的能量值增加一点,使得能打败当前的敌人,其实就是贪心
时间复杂度 O ( n m l g ( n m ) ) O(nmlg(nm)) O(nmlg(nm))
#include<bits/stdc++.h>
using namespace std;#define ll long long
#define endl "\n"ll n,m,x,y;
ll grid[1005][1005] ={0};
ll vis[1005][1005] ={0};
bool ifon(ll x,ll y){return x>=0&&x<n&&y>=0&&y<m;
}ll cal(ll md){ll ans = md;for(ll i=0;i<n;i++)for(ll j=0;j<m;j++)vis[i][j] = 0;vis[x][y] = 1;priority_queue<pair<ll,pair<ll,ll>>,vector<pair<ll,pair<ll,ll>>>,greater<pair<ll,pair<ll,ll>>>> pq;pq.push({0,{x,y}});ll dx[4] = {-1,1,0,0};ll dy[4] = {0,0,-1,1};ll arr = 0;while(pq.size()){auto pp = pq.top();pq.pop();if(md<pp.first){ans += pp.first-md;md = pp.first;}arr +=1;md += pp.first;ll nx = pp.second.first,ny = pp.second.second;for(ll i=0;i<4;i++){ll tox = dx[i]+nx;ll toy = dy[i]+ny;if(!ifon(tox,toy)) continue;if(vis[tox][toy]) continue;vis[tox][toy] = 1;pq.push({grid[tox][toy],{tox,toy}});}}return ans;
}void solve(){cin>>n>>m>>x>>y;x--;y--;for(ll i=0;i<n;i++)for(ll j=0;j<m;j++) cin>>grid[i][j];ll st = grid[x][y];grid[x][y] = 0;ll ans = cal(st);if(ans <= st){cout<<"No cheating need."<<endl;} elsecout<<ans<<endl;
}signed main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);ll t = 1;while(t--){solve();}
}
K .有趣的BOSS
素数分解+思维
1、要么/=2
2、要么刚好砍到0
3、那么就是每一步判断有没有机会刚好砍到0
4、直接从n中取出某个素数,并且把这种素数取完得到l,剩下的是n/l,然后计算l+n/l是否小于等于n,如果是这样的话,怪兽二受到n点伤害,怪兽1收到l+n/l点伤害,不够怎么办呢?没事,直接补1,补到n为止
5、如果4不行,那么直接用很多很强的到,把两只都砍到0以下
#include<bits/stdc++.h>using namespace std;#define ll long long
#define endl "\n"void solve(){int n;cin>>n;int cnt = 0;while(n){if(n==1){cout<<cnt+1<<endl;return;}for(int i=2;i*i<=n;i++){if(n%i==0){int ts = 0;int nn = n;int l =1;while(nn%i==0) ts++,nn/=i,l*=i;if(l+nn<=n){cout<<cnt+1<<endl;return;}else break;}}n>>=1;cnt++;}
}int main(){cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);int t = 1;cin>>t;while(t--){solve();}
}
相关文章:

【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
文章目录 【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛A.星期几考试?C.信件D、乘除法E、不知道叫什么名字F.我要学会盾反!G.闪闪发光心动不已!H.不想想背景的gcdI.uu爱玩飞行棋J.火柴人小游戏K .有趣的BOSS 【LittleXi】2023年广东…...

【C语言:数据在内存中的存储】
文章目录 1.整数在内存中的存储1.1整数在内存中的存储1.2整型提升 2.大小端字节序2.1什么是大小端2.2为什么有大小端之分 3.整数在内存中的存储相关题目题目一题目二题目三题目四题目五题目六题目七 4.浮点数在内存中的存储4.1浮点数存的过程4.2浮点数取得过程 在这之前呢&…...

每日一练:阿姆斯特朗数
如果一个 n 位正整数等于其各位数字的 n 次方之和,则称该数为阿姆斯特朗数。 例如 1^3 5^3 3^3 153。 1000 以内的阿姆斯特朗数: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407。...
)
fatal: remote error: upload-pack: not our ref (未解决问题)
PX4使用 git submodule update --init --recursive报错 fatal: remote error: upload-pack: not our ref解决办法参考:https://stackoverflow.com/questions/61163082/why-does-git-submodule-update-fail-with-fatal-remote-error-upload-pack-not-o 感觉就是清…...
、readline()、readlines() 函数 读取文件)
Python 3 使用 read()、readline()、readlines() 函数 读取文件
1 样例文件 example.txt 春晓 孟浩然〔唐代〕 春眠不觉晓,处处闻啼鸟。 夜来风雨声,花落知多少。 2 分别使用 read()、readline()、readlines() 函数 2.1 # read() -------- 一次性读取所有文本,以字符串的形式返回结果。 # read() ----…...
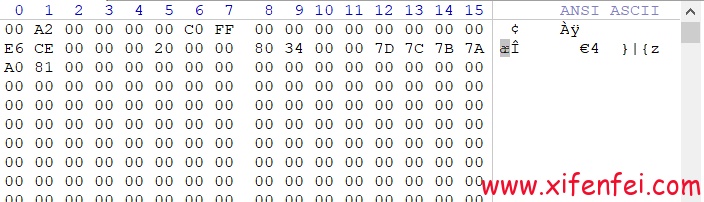
勒索解密后oracle无法启动故障处理----惜分飞
客户linux平台被勒索病毒加密,其中有oracle数据库.客户联系黑客进行解密【勒索解密oracle失败】,但是数据库无法正常启动,dbv检查数据库文件报错 [oraclehisdb ~]$ dbv filesystem01.dbf DBVERIFY: Release 11.2.0.1.0 - Production on 星期一 11月 27 21:49:17 2023 Copyrig…...
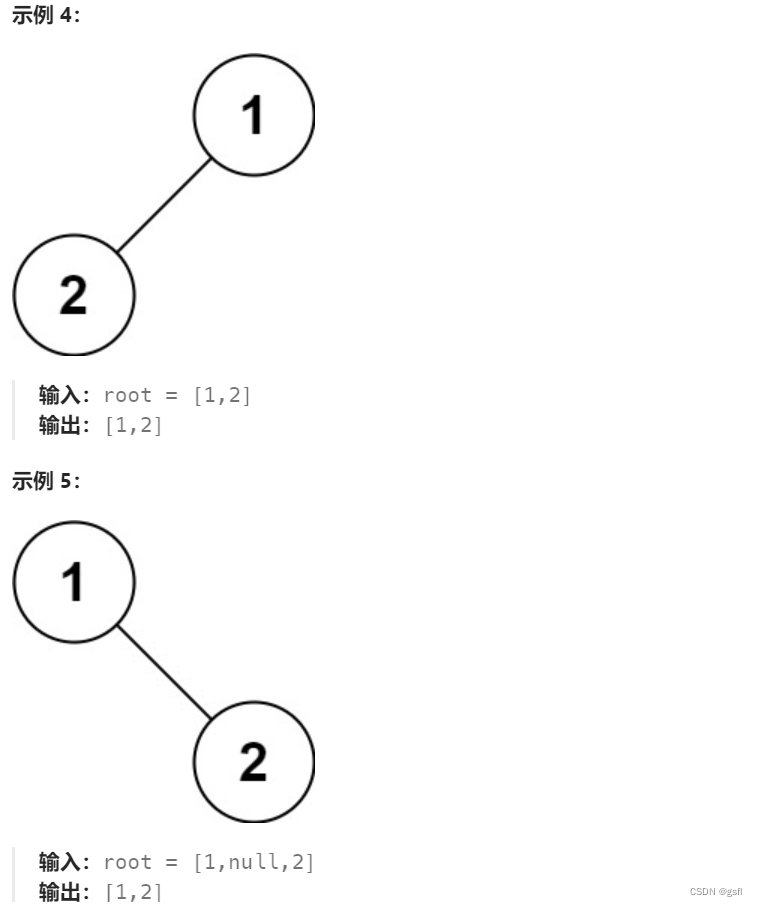
Leetcode144. 二叉树的前序遍历-C语言
文章目录 题目介绍题目分析解题思路1.创建一个数组来储存二叉树节点的值2.根据二叉树的大小来开辟数组的大小3.边前序遍历边向创建的数组中存入二叉树节点的值 完整代码 题目介绍 题目分析 题目要求我们输出二叉树按前序遍历排列的每个节点的值。 解题思路 1.创建一个数组来…...

dmesg命令在软件测试中的实际应用
简介:当你想要了解 Linux 系统在启动时究竟发生了什么?或者当硬件设备不工作时,如何进行调试?这就是 dmesg 命令的用武之地。本文将介绍 dmesg 的基本功能,并深入探讨其在软件测试中的实际应用。 历史攻略:…...

【渗透】记录阿里云CentOS一次ddos攻击
文章目录 发现防御 发现 防御 流量清洗 使用高防...
)
前端面试提问(3)
1、js两个数相加会不会丢精度? 可能会遇到精度丢失的问题。JavaScript 使用的是 IEEE 754 浮点数标准,即一种二进制表示法,有时不能准确地表示十进制小数。如果你需要进行精确的十进制数值计算,可以使用一些处理精确数值的库&…...
fl studio21.2最新汉化中文完整版网盘下载
fl studio 21中文版是Image-Line公司继20版本之后更新的水果音乐制作软件,很多用户不太理解,为什么新版本不叫fl studio 21或fl studio2024,非得直接跳到21.2版本,其实该版本是为了纪念该公司22周年,所以该版本也是推出…...

差分数组相关知识点以及刷题
差分数组 差分数组是什么? **举例:**对于数组考虑数组 a[1,3,3,5,8],对其中的相邻元素两两作差(右边减左边),得到数组 [2,0,2,3]。然后在开头补上 a[0],得到差分数组: d[1,2,0…...
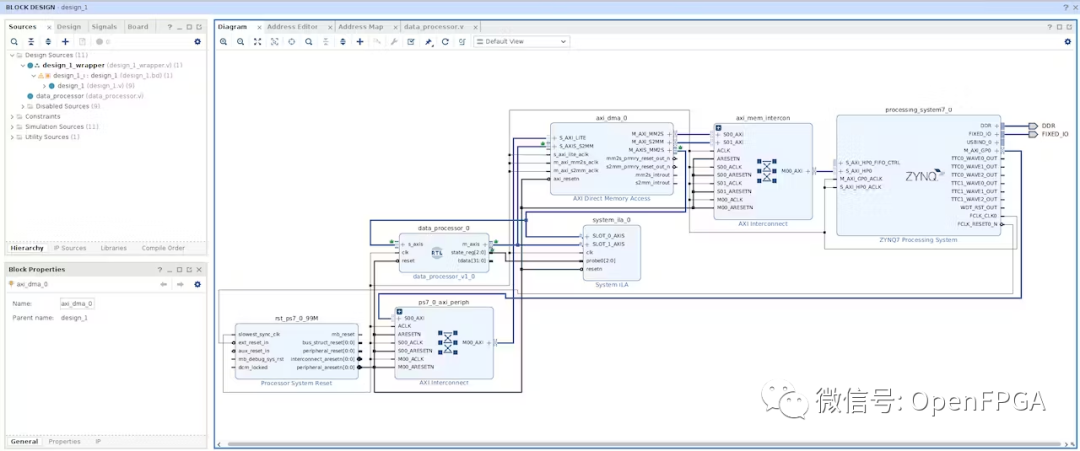
使用 DMA 在 FPGA 中的 HDL 和嵌入式 C 之间传输数据
使用 DMA 在 FPGA 中的 HDL 和嵌入式 C 之间传输数据 该项目介绍了如何在 PL 中的 HDL 与 FPGA 中的处理器上运行的嵌入式 C 之间传输数据的基本结构。 介绍 鉴于机器学习和人工智能等应用的 FPGA 设计中硬件加速的兴起,现在是剥开几层“云雾”并讨论 HDL 之间来回传…...

uniapp地图基本使用及解决添加markers不生效问题?
uniapp地图使用 App端 通过 nvue 页面实现地图 文章目录 uniapp地图使用效果图templatejs添加 marker使用地图查看位置移到到当前位置 效果图 template <template><view class"mapWrap"><!-- #ifdef APP-NVUE --><map class"map-containe…...
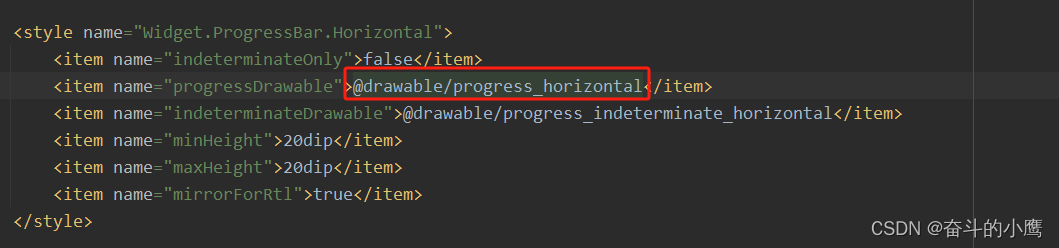
使用系统ProgressBar实现三色进度条
使用系统ProgressBar实现如图三色进度条: //布局中<ProgressBarandroid:layout_width"0dp"android:layout_height"8dp"android:layout_marginLeft"16dp"app:layout_constraintBottom_toBottomOf"id/photo"app:layout_c…...

Vue3中的组合式API的详细教程和介绍
文章目录 前言介绍组合式 API 基础setup 组件选项 带 ref 的响应式变量生命周期钩子注册内部 setupwatch 响应式更改独立的 computed 属性后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:vue.js 🐱👓博主在前端…...
Java后端开发——JDBC(万字详解)
Java后端开发——JDBC(万字详解) 今日目标 掌握JDBC的的CRUD理解JDBC中各个对象的作用掌握Druid的使用 1,JDBC概述 在开发中我们使用的是java语言,那么势必要通过java语言操作数据库中的数据。这就是接下来要学习的JDBC。 1.1 …...
python etree.HTML 以及xpath 解析网页的工具
文章目录 导入模块相关语法实战 导入模块 from lxml import etree相关语法 XPath(XML Path Language)是一种用于在XML文档中定位和选择元素的语言。XPath的主要应用领域是在XML文档中进行导航和查询,通常用于在XML中选择节点或节点集合。以…...
待编辑)
电机伺服驱动学习笔记(7)待编辑
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、pandas是什么?二、使用步骤1.引入库2.读入数据 总结 前言 提示:这里可以添加本文要记录的大概内容: 例如:…...

【云备份】业务处理
文章目录 1. 业务处理作用功能 2. 代码框架编写构造函数UpLoad ——文件上传请求ListShow —— 展示页面请求处理实现Download —— 下载请求的处理实现断点续传实现 1. 业务处理 作用 业务处理模块是对客户端的业务请求进行处理 功能 1.文件上传请求:备份客户端…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...
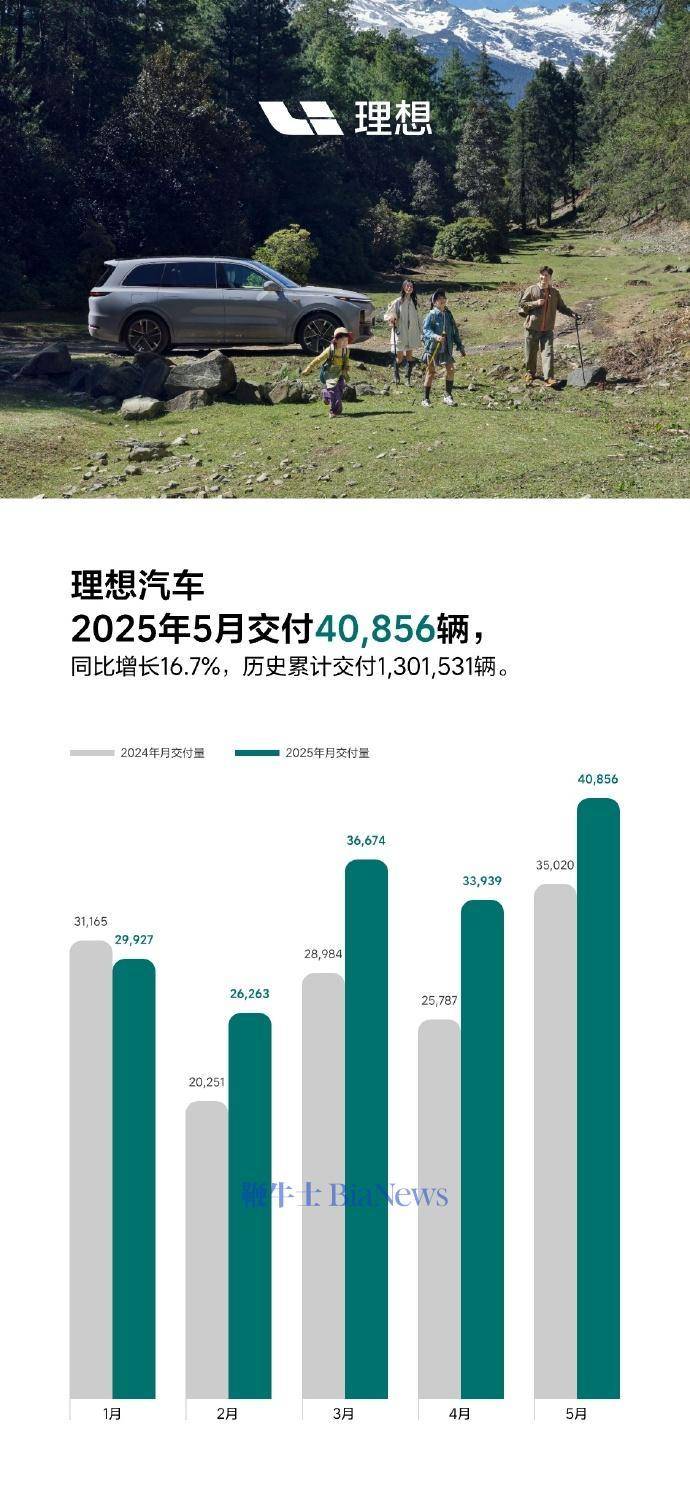
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...
