逆波兰表达式求值[中等]
优质博文:IT-BLOG-CN
一、题目
给你一个字符串数组tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用32位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
1 <= tokens.length <= 104
tokens[i]是一个算符(“+”、“-”、“*” 或 “/”),或是在范围[-200, 200]内的一个整数
逆波兰表达式由波兰的逻辑学家卢卡西维兹提出。逆波兰表达式的特点是:没有括号,运算符总是放在和它相关的操作数之后。因此,逆波兰表达式也称后缀表达式。
二、代码
【1】栈: 逆波兰表达式严格遵循「从左到右」的运算。计算逆波兰表达式的值时,使用一个栈存储操作数,从左到右遍历逆波兰表达式,进行如下操作:如果遇到操作数,则将操作数入栈;如果遇到运算符,则将两个操作数出栈,其中先出栈的是右操作数,后出栈的是左操作数,使用运算符对两个操作数进行运算,将运算得到的新操作数入栈。整个逆波兰表达式遍历完毕之后,栈内只有一个元素,该元素即为逆波兰表达式的值。
class Solution {public int evalRPN(String[] tokens) {Deque<Integer> stack = new LinkedList<Integer>();int n = tokens.length;for (int i = 0; i < n; i++) {String token = tokens[i];if (isNumber(token)) {stack.push(Integer.parseInt(token));} else {int num2 = stack.pop();int num1 = stack.pop();switch (token) {case "+":stack.push(num1 + num2);break;case "-":stack.push(num1 - num2);break;case "*":stack.push(num1 * num2);break;case "/":stack.push(num1 / num2);break;default:}}}return stack.pop();}public boolean isNumber(String token) {return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));}
}
时间复杂度: O(n),其中n是数组tokens的长度。需要遍历数组tokens一次,计算逆波兰表达式的值。
空间复杂度: O(n),其中n是数组tokens的长度。使用栈存储计算过程中的数,栈内元素个数不会超过逆波兰表达式的长度。
【2】数组模拟栈: 方法一使用栈存储操作数。也可以使用一个数组模拟栈操作。如果使用数组代替栈,则需要预先定义数组的长度。对于长度为n的逆波兰表达式,显然栈内元素个数不会超过n,但是将数组的长度定义为n仍然超过了栈内元素个数的上界。那么,栈内元素最多可能有多少个?
对于一个有效的逆波兰表达式,其长度n一定是奇数,且操作数的个数一定比运算符的个数多1个,即包含(n+1)/2个操作数和(n−1)/2个运算符。考虑遇到操作数和运算符时,栈内元素个数分别会如何变化:
1、如果遇到操作数,则将操作数入栈,因此栈内元素增加1个;
2、如果遇到运算符,则将两个操作数出栈,然后将一个新操作数入栈,因此栈内元素先减少2个再增加1个,结果是栈内元素减少1个。
由此可以得到操作数和运算符与栈内元素个数变化的关系:遇到操作数时,栈内元素增加1个;遇到运算符时,栈内元素减少1个。
最坏情况下,(n+1)/2个操作数都在表达式的前面,(n−1)/2个运算符都在表达式的后面,此时栈内元素最多为(n+1)/2个。在其余情况下,栈内元素总是少于(n+1)/2个。因此,在任何情况下,栈内元素最多可能有(n+1)/2个,将数组的长度定义为(n+1)/2即可。
具体实现方面,创建数组stack模拟栈,数组下标0的位置对应栈底,定义index表示栈顶元素的下标位置,初始时栈为空,index=−1。当遇到操作数和运算符时,进行如下操作:
1、如果遇到操作数,则将index的值加1,然后将操作数赋给stack[index];
2、如果遇到运算符,则将index的值减1,此时stack[index]和stack[index+1]的元素分别是左操作数和右操作数,使用运算符对两个操作数进行运算,将运算得到的新操作数赋给stack[index]。
整个逆波兰表达式遍历完毕之后,栈内只有一个元素,因此index=0,此时stack[index]即为逆波兰表达式的值。
class Solution {public int evalRPN(String[] tokens) {int n = tokens.length;int[] stack = new int[(n + 1) / 2];int index = -1;for (int i = 0; i < n; i++) {String token = tokens[i];switch (token) {case "+":index--;stack[index] += stack[index + 1];break;case "-":index--;stack[index] -= stack[index + 1];break;case "*":index--;stack[index] *= stack[index + 1];break;case "/":index--;stack[index] /= stack[index + 1];break;default:index++;stack[index] = Integer.parseInt(token);}}return stack[index];}
}
时间复杂度: O(n),其中n是数组tokens的长度。需要遍历数组tokens一次,计算逆波兰表达式的值。
空间复杂度: O(n),其中n是数组tokens的长度。需要创建长度为(n+1)/2的数组模拟栈操作。
相关文章:

逆波兰表达式求值[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个字符串数组tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。 有效的算符为 ‘’、‘-’、‘*’ 和 ‘/’ 。 每个操作数(运算对象)都…...

Oracle连接和使用
5. Oracle连接和使用 5.1. sqlplus sqlplus作为甲骨文公司提供的一款本族工具产品,有着悠久的历史和积淀,它几乎伴随着Oracle数据库产生至今的整个生命周期,而且,还会继续和Oracle数据库产品相伴一直发展下去。该工具看似简单灵活的背后,却为广大用户使用Oracle数据库提…...

redis单线程为什么这么快
redis单线程为什么这么快 redis是使用的单线程来进行操作的,因为所有的数据都是在内存中的,内存操作特别快。而且单线程避免了多线程切换性能损耗问题 单线程如何处理并发客户端连接? redis利用epoll来实现IO多路复用,将连接信息和…...
工业机器视觉megauging(向光有光)使用说明书(五,轻量级的visionpro)
这个说明主要介绍抓线功能。 第一步,添加线工具,鼠标双击工具箱“抓线”,出现如下界面: 第二步,我们拉一条,“九点标定”到“抓线1”的线,和visionpro操作一样: 第三步,…...

【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
文章目录 【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛A.星期几考试?C.信件D、乘除法E、不知道叫什么名字F.我要学会盾反!G.闪闪发光心动不已!H.不想想背景的gcdI.uu爱玩飞行棋J.火柴人小游戏K .有趣的BOSS 【LittleXi】2023年广东…...

【C语言:数据在内存中的存储】
文章目录 1.整数在内存中的存储1.1整数在内存中的存储1.2整型提升 2.大小端字节序2.1什么是大小端2.2为什么有大小端之分 3.整数在内存中的存储相关题目题目一题目二题目三题目四题目五题目六题目七 4.浮点数在内存中的存储4.1浮点数存的过程4.2浮点数取得过程 在这之前呢&…...

每日一练:阿姆斯特朗数
如果一个 n 位正整数等于其各位数字的 n 次方之和,则称该数为阿姆斯特朗数。 例如 1^3 5^3 3^3 153。 1000 以内的阿姆斯特朗数: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407。...
)
fatal: remote error: upload-pack: not our ref (未解决问题)
PX4使用 git submodule update --init --recursive报错 fatal: remote error: upload-pack: not our ref解决办法参考:https://stackoverflow.com/questions/61163082/why-does-git-submodule-update-fail-with-fatal-remote-error-upload-pack-not-o 感觉就是清…...
、readline()、readlines() 函数 读取文件)
Python 3 使用 read()、readline()、readlines() 函数 读取文件
1 样例文件 example.txt 春晓 孟浩然〔唐代〕 春眠不觉晓,处处闻啼鸟。 夜来风雨声,花落知多少。 2 分别使用 read()、readline()、readlines() 函数 2.1 # read() -------- 一次性读取所有文本,以字符串的形式返回结果。 # read() ----…...
勒索解密后oracle无法启动故障处理----惜分飞
客户linux平台被勒索病毒加密,其中有oracle数据库.客户联系黑客进行解密【勒索解密oracle失败】,但是数据库无法正常启动,dbv检查数据库文件报错 [oraclehisdb ~]$ dbv filesystem01.dbf DBVERIFY: Release 11.2.0.1.0 - Production on 星期一 11月 27 21:49:17 2023 Copyrig…...
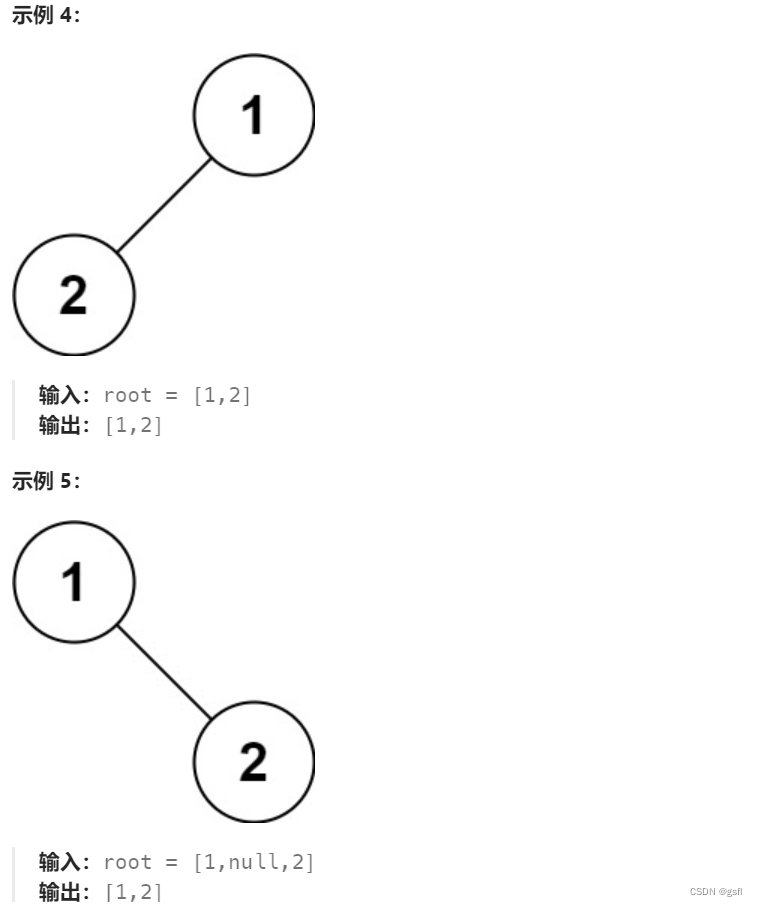
Leetcode144. 二叉树的前序遍历-C语言
文章目录 题目介绍题目分析解题思路1.创建一个数组来储存二叉树节点的值2.根据二叉树的大小来开辟数组的大小3.边前序遍历边向创建的数组中存入二叉树节点的值 完整代码 题目介绍 题目分析 题目要求我们输出二叉树按前序遍历排列的每个节点的值。 解题思路 1.创建一个数组来…...

dmesg命令在软件测试中的实际应用
简介:当你想要了解 Linux 系统在启动时究竟发生了什么?或者当硬件设备不工作时,如何进行调试?这就是 dmesg 命令的用武之地。本文将介绍 dmesg 的基本功能,并深入探讨其在软件测试中的实际应用。 历史攻略:…...

【渗透】记录阿里云CentOS一次ddos攻击
文章目录 发现防御 发现 防御 流量清洗 使用高防...
)
前端面试提问(3)
1、js两个数相加会不会丢精度? 可能会遇到精度丢失的问题。JavaScript 使用的是 IEEE 754 浮点数标准,即一种二进制表示法,有时不能准确地表示十进制小数。如果你需要进行精确的十进制数值计算,可以使用一些处理精确数值的库&…...
fl studio21.2最新汉化中文完整版网盘下载
fl studio 21中文版是Image-Line公司继20版本之后更新的水果音乐制作软件,很多用户不太理解,为什么新版本不叫fl studio 21或fl studio2024,非得直接跳到21.2版本,其实该版本是为了纪念该公司22周年,所以该版本也是推出…...

差分数组相关知识点以及刷题
差分数组 差分数组是什么? **举例:**对于数组考虑数组 a[1,3,3,5,8],对其中的相邻元素两两作差(右边减左边),得到数组 [2,0,2,3]。然后在开头补上 a[0],得到差分数组: d[1,2,0…...
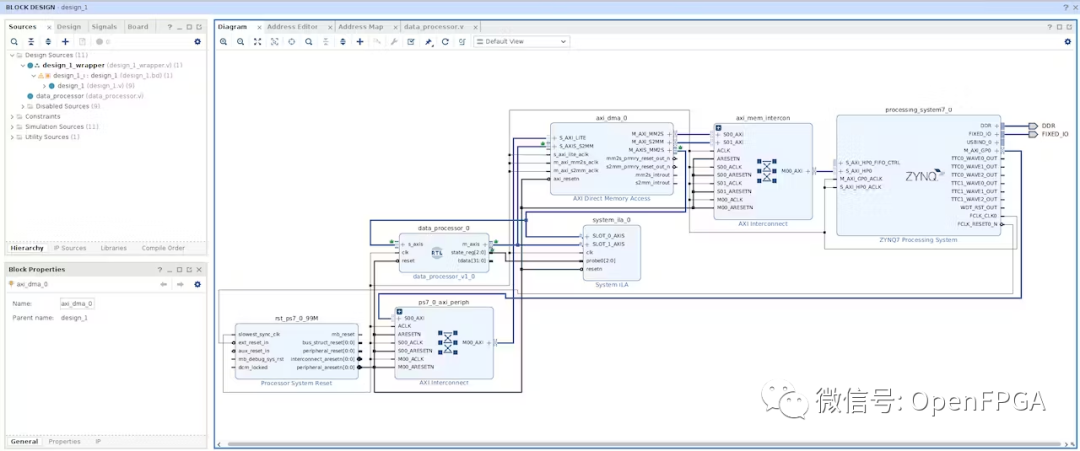
使用 DMA 在 FPGA 中的 HDL 和嵌入式 C 之间传输数据
使用 DMA 在 FPGA 中的 HDL 和嵌入式 C 之间传输数据 该项目介绍了如何在 PL 中的 HDL 与 FPGA 中的处理器上运行的嵌入式 C 之间传输数据的基本结构。 介绍 鉴于机器学习和人工智能等应用的 FPGA 设计中硬件加速的兴起,现在是剥开几层“云雾”并讨论 HDL 之间来回传…...

uniapp地图基本使用及解决添加markers不生效问题?
uniapp地图使用 App端 通过 nvue 页面实现地图 文章目录 uniapp地图使用效果图templatejs添加 marker使用地图查看位置移到到当前位置 效果图 template <template><view class"mapWrap"><!-- #ifdef APP-NVUE --><map class"map-containe…...
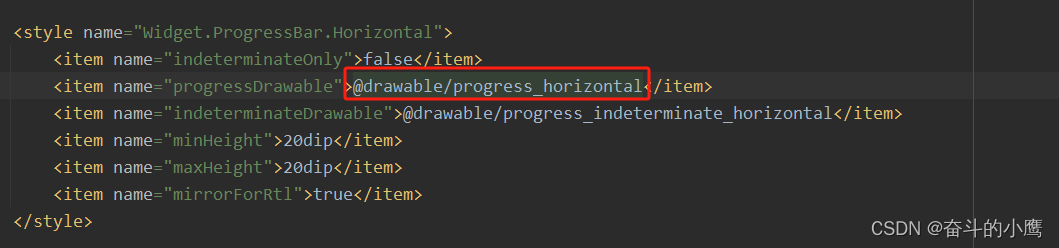
使用系统ProgressBar实现三色进度条
使用系统ProgressBar实现如图三色进度条: //布局中<ProgressBarandroid:layout_width"0dp"android:layout_height"8dp"android:layout_marginLeft"16dp"app:layout_constraintBottom_toBottomOf"id/photo"app:layout_c…...

Vue3中的组合式API的详细教程和介绍
文章目录 前言介绍组合式 API 基础setup 组件选项 带 ref 的响应式变量生命周期钩子注册内部 setupwatch 响应式更改独立的 computed 属性后言 前言 hello world欢迎来到前端的新世界 😜当前文章系列专栏:vue.js 🐱👓博主在前端…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
