线性可分SVM摘记
线性可分SVM摘记
- 0. 线性可分
- 1. 训练样本到分类面的距离
- 2. 函数间隔和几何间隔、(硬)间隔最大化
- 3. 支持向量
\qquad 线性可分的支持向量机是一种二分类模型,支持向量机通过核技巧可以成为非线性分类器。本文主要分析了线性可分的支持向量机模型,主要取自于李航《统计学习方法》第七章。
0. 线性可分
\qquad 如下图所示,考虑训练数据“线性可分”的情况:
\qquad 
\qquad 假设分类面 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 可以将两类数据完整分开,任一训练样本 x \boldsymbol x x 的输出值(目标值) y y y 满足:
y = sgn ( w T x + b ) = { + 1 , w T x + b > 0 ( x ∈ ℓ 1 ) − 1 , w T x + b < 0 ( x ∈ ℓ 2 ) \qquad\qquad\qquad y=\text{sgn}(\boldsymbol w^T\boldsymbol x+b)=\begin{cases}+1,\quad\boldsymbol w^T\boldsymbol x+b>0\ (\boldsymbol x\in\ell_1)\\-1,\quad\boldsymbol w^T\boldsymbol x+b<0\ (\boldsymbol x\in\ell_2)\end{cases} y=sgn(wTx+b)={+1,wTx+b>0 (x∈ℓ1)−1,wTx+b<0 (x∈ℓ2)
\qquad
1. 训练样本到分类面的距离
\qquad 任一样本 x \boldsymbol x x 到分类面的垂直距离为: r = y ( w T x + b ) ∥ w ∥ r=\dfrac{y(\boldsymbol w^T\boldsymbol{x}+b)}{\Vert\boldsymbol w\Vert} r=∥w∥y(wTx+b)
∙ \quad\bullet ∙ 正例 x i \boldsymbol x_i xi(满足 w T x i + b > 0 , y i = + 1 \boldsymbol w^T\boldsymbol x_i+b>0,\ y_i=+1 wTxi+b>0, yi=+1)
\qquad\qquad 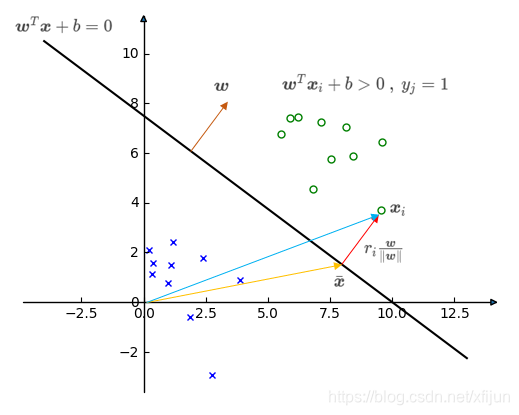
\qquad 假设 x i \boldsymbol x_i xi 到分类面的距离为 r i r_i ri,向量 x ˉ \bar{\boldsymbol x} xˉ 在分类面(满足 w T x ˉ + b = 0 \boldsymbol{w}^T\bar{\boldsymbol{x}}+b=0 wTxˉ+b=0),显然 x i = x ˉ + r i w ∥ w ∥ \boldsymbol x_i=\bar{\boldsymbol x}+r_i\dfrac{\boldsymbol w}{\Vert\boldsymbol w\Vert} xi=xˉ+ri∥w∥w
\qquad 那么
w T x i + b = w T ( x ˉ + r i w ∥ w ∥ ) + b = w T x ˉ + b + w T r i w ∥ w ∥ = r i w T w ∥ w ∥ = r i ∥ w ∥ \qquad\qquad\qquad\begin{aligned}\boldsymbol w^T\boldsymbol x_i+b&=\boldsymbol w^T(\bar{\boldsymbol x}+r_i\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert})+b\\ &=\boldsymbol w^T\bar{\boldsymbol x}+b+\boldsymbol w^Tr_i\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=r_i\frac{\boldsymbol w^T\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=r_i\Vert\boldsymbol w\Vert\end{aligned} wTxi+b=wT(xˉ+ri∥w∥w)+b=wTxˉ+b+wTri∥w∥w=ri∥w∥wTw=ri∥w∥
\qquad 可得到正例 x i \boldsymbol x_i xi 到分类面的垂直距离 r i = w T x i + b ∥ w ∥ r_i=\dfrac{\boldsymbol w^T\boldsymbol x_i+b}{\Vert\boldsymbol w\Vert} ri=∥w∥wTxi+b
\qquad
∙ \quad\bullet ∙ 负例 x j \boldsymbol x_j xj(满足 w T x j + b < 0 , y j = − 1 \boldsymbol w^T\boldsymbol x_j+b<0,\ y_j=-1 wTxj+b<0, yj=−1)
\qquad\qquad 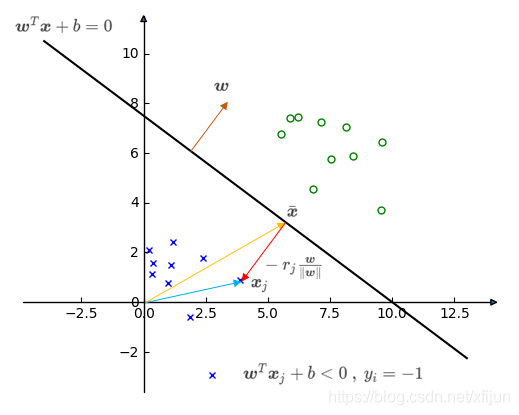
\qquad 假设 x j \boldsymbol x_j xj 到分类面的距离为 r j r_j rj,向量 x ˉ \bar{\boldsymbol x} xˉ 在分类面(满足 w T x ˉ + b = 0 \boldsymbol w^T\bar{\boldsymbol x}+b=0 wTxˉ+b=0),显然 x j = x ˉ − r j w ∥ w ∥ \boldsymbol x_j=\bar{\boldsymbol x}-r_j\dfrac{\boldsymbol w}{\Vert\boldsymbol w\Vert} xj=xˉ−rj∥w∥w
\qquad 那么
w T x j + b = w T ( x ˉ − r j w ∥ w ∥ ) + b = w T x ˉ + b − w T r j w ∥ w ∥ = − r j w T w ∥ w ∥ = − r j ∥ w ∥ \qquad\qquad\qquad\begin{aligned}\boldsymbol w^T\boldsymbol x_j+b&=\boldsymbol w^T(\bar{\boldsymbol x}-r_j\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert})+b\\ &=\boldsymbol w^T\bar{\boldsymbol x}+b-\boldsymbol w^Tr_j\frac{\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=-r_j\frac{\boldsymbol w^T\boldsymbol w}{\Vert\boldsymbol w\Vert}\\ &=-r_j\Vert\boldsymbol w\Vert\end{aligned} wTxj+b=wT(xˉ−rj∥w∥w)+b=wTxˉ+b−wTrj∥w∥w=−rj∥w∥wTw=−rj∥w∥
\qquad 可得到负例 x j \boldsymbol x_j xj 到分类面的垂直距离 r j = − w T x j + b ∥ w ∥ r_j=-\dfrac{\boldsymbol w^T\boldsymbol x_j+b}{\Vert\boldsymbol w\Vert} rj=−∥w∥wTxj+b
\qquad
2. 函数间隔和几何间隔、(硬)间隔最大化
\qquad 由于任一训练样本 x i \boldsymbol x_i xi 的输出值 y y y 满足: y = { + 1 , w T x i + b > 0 ( ∀ x i ∈ ℓ 1 ) − 1 , w T x i + b < 0 ( ∀ x i ∈ ℓ 2 ) y=\begin{cases}+1,\quad\boldsymbol w^T\boldsymbol x_i+b>0\ \ (\forall\ \boldsymbol x_i\in\ell_1)\\-1,\quad\boldsymbol w^T\boldsymbol x_i+b<0\ \ (\forall\ \boldsymbol x_i\in\ell_2)\end{cases} y={+1,wTxi+b>0 (∀ xi∈ℓ1)−1,wTxi+b<0 (∀ xi∈ℓ2),可定义两种间隔 ( margin ) (\text{margin}) (margin)来描述“训练样本 x i \boldsymbol x_i xi 到分类面的远近”。
\qquad
∙ \quad\bullet ∙ 函数间隔 ( functional margin ) (\text{functional margin}) (functional margin)
γ ^ i = y i ( w T x i + b ) = ∣ w T x i + b ∣ \qquad\qquad\hat{\gamma}_i=y_i(\boldsymbol w^T\boldsymbol x_i+b)=\vert\boldsymbol w^T\boldsymbol x_i+b\vert γ^i=yi(wTxi+b)=∣wTxi+b∣
函数间隔只能够相对地描述“训练样本 x i \boldsymbol x_i xi 到分类面的远近”。
例如, H 1 : w T x + b = 0 \mathcal H_1:\ \boldsymbol w^T\boldsymbol x+b=0 H1: wTx+b=0 与 H 2 : λ w T x + λ b = 0 \mathcal H_2:\ \lambda\boldsymbol w^T\boldsymbol x+\lambda b=0 H2: λwTx+λb=0 实际上是指同一个分类面(假设 λ > 0 \lambda>0 λ>0)
对训练样本 x i \boldsymbol x_i xi 而言,却有 { γ ^ 1 i = ∣ w T x i + b ∣ γ ^ 2 i = λ ∣ w T x i + b ∣ \begin{cases}\hat{\gamma}_{1i}=\vert\boldsymbol w^T\boldsymbol x_i+b\vert\\ \hat{\gamma}_{2i}=\lambda\vert\boldsymbol w^T\boldsymbol x_i+b\vert \end{cases} {γ^1i=∣wTxi+b∣γ^2i=λ∣wTxi+b∣,函数间隔 γ ^ 2 i = λ γ ^ 1 i \hat{\gamma}_{2i}=\lambda\hat{\gamma}_{1i} γ^2i=λγ^1i
\qquad
∙ \quad\bullet ∙ 几何间隔 ( geometricl margin ) (\text{geometricl margin}) (geometricl margin)
γ i = y i r i = y i ( w T x i + b ) ∥ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ \qquad\qquad \gamma_i=y_ir_i=\dfrac{y_i(\boldsymbol w^T\boldsymbol x_i+b)}{\Vert\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} γi=yiri=∥w∥yi(wTxi+b)=∥w∥∣wTxi+b∣
几何间隔就是“训练样本 x i \boldsymbol x_i xi 到分类面的垂直距离”,也就是“规范化的函数间隔”。
上例中, { γ 1 i = γ ^ 1 i ∥ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ γ 2 i = γ ^ 2 i ∥ λ w ∥ = λ ∣ w T x i + b ∣ ∥ λ w ∥ = ∣ w T x i + b ∣ ∥ w ∥ \begin{cases}\gamma_{1i}=\dfrac{\hat{\gamma}_{1i}}{\Vert\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} \\ \\\gamma_{2i}=\dfrac{\hat{\gamma}_{2i}}{\Vert\lambda\boldsymbol w\Vert}=\dfrac{\lambda\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\lambda\boldsymbol w\Vert}=\dfrac{\vert\boldsymbol w^T\boldsymbol x_i+b\vert}{\Vert\boldsymbol w\Vert} \end{cases} ⎩ ⎨ ⎧γ1i=∥w∥γ^1i=∥w∥∣wTxi+b∣γ2i=∥λw∥γ^2i=∥λw∥λ∣wTxi+b∣=∥w∥∣wTxi+b∣,几何间隔 γ 1 i = γ 2 i \gamma_{1i}=\gamma_{2i} γ1i=γ2i,仍然相等。
\qquad 显然,函数间隔和几何间隔之间的关系为:
γ = γ ^ ∥ w ∥ \qquad\qquad\textcolor{crimson}{\gamma=\dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert}} γ=∥w∥γ^
\qquad
∙ \quad\bullet ∙ 以最大化训练样本的几何间隔为目标函数,并定义约束最优化问题
\qquad 约束最优化问题(1)
max w , b γ s . t . y i ( w T x i + b ) ∥ w ∥ ≥ γ , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\max_{\boldsymbol w,b}\ \gamma\\ &\ s.t.\ \ \ \dfrac{y_i(\boldsymbol w^T\boldsymbol x_i+b)}{\Vert\boldsymbol w\Vert}\ge \gamma,\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmax γ s.t. ∥w∥yi(wTxi+b)≥γ,∀ xi
也就是,在确保所有训练样本到分类面的垂直距离都大于 γ \gamma γ 的前提下,尽可能让(几何)间隔最大。
\qquad 利用两种间隔之间的关系 γ = γ ^ ∥ w ∥ \gamma=\dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert} γ=∥w∥γ^,在约束最优化问题(1)中使用函数间隔 γ ^ \hat{\gamma} γ^ 来描述几何间隔 γ \gamma γ,也就是
\qquad 约束最优化问题(2)
max w , b γ ^ ∥ w ∥ s . t . y i ( w T x i + b ) ≥ γ ^ , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{\hat{\gamma}}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat{\gamma},\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmax ∥w∥γ^ s.t. yi(wTxi+b)≥γ^,∀ xi
\qquad
\qquad 考虑满足约束最优化问题(2)的同一个分类面的两种表示 H 1 : ( w , b ) \mathcal H_1:(\boldsymbol w,b) H1:(w,b) 和 H 2 : ( λ w , λ b ) \mathcal H_2:(\lambda\boldsymbol w,\lambda b) H2:(λw,λb),对于任一训练样本 x i \boldsymbol x_i xi 而言( λ > 0 \lambda>0 λ>0),那么:
\qquad ① H 1 : w T x + b = 0 \quad\textcolor{firebrick}{\mathcal H_1}:\ \boldsymbol w^T\boldsymbol x+b=0 H1: wTx+b=0 (函数间隔为 γ ^ = ∣ w T x i + b ∣ \hat\gamma=\vert\boldsymbol w^T\boldsymbol x_i+b\vert γ^=∣wTxi+b∣)
⟹ { 目标函数值: γ ^ ∥ w ∥ 约束函数: y i ( w T x i + b ) ≥ γ ^ , ∀ x i \qquad\qquad\quad\Longrightarrow\quad\begin{cases}目标函数值:\quad\dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert}\\ 约束函数: \quad y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat\gamma,\quad \forall\ \boldsymbol x_i\end{cases} ⟹⎩ ⎨ ⎧目标函数值:∥w∥γ^约束函数: yi(wTxi+b)≥γ^,∀ xi
\qquad ② H 2 : λ w T x + λ b = 0 \quad\textcolor{firebrick}{\mathcal H_2}:\ \lambda\boldsymbol w^T\boldsymbol x+\lambda b=0 H2: λwTx+λb=0 (函数间隔为 λ γ ^ \lambda\hat\gamma λγ^)
⟹ { 目标函数值: λ γ ^ ∥ λ w ∥ 约束函数: y i λ ( w T x i + b ) ≥ λ γ ^ , ∀ x i \qquad\qquad\quad\Longrightarrow\quad\begin{cases}目标函数值:\quad\dfrac{\lambda\hat\gamma}{\Vert\lambda\boldsymbol w\Vert}\\ 约束函数: \quad y_i\lambda(\boldsymbol w^T\boldsymbol x_i+b) \ge \lambda\hat\gamma,\quad \forall\ \boldsymbol x_i\end{cases} ⟹⎩ ⎨ ⎧目标函数值:∥λw∥λγ^约束函数: yiλ(wTxi+b)≥λγ^,∀ xi
\qquad
\qquad 显然,权值 ( w , b ) (\boldsymbol w,b) (w,b) 与其同比例的缩放值 ( λ w , λ b ) (\lambda\boldsymbol w,\lambda b) (λw,λb) 对于约束最优化问题(2)而言是没有影响的。
\qquad
∙ \quad\bullet ∙ 构造凸二次规划问题
\qquad 在约束最优化问题(2)中,可以简单地取函数间隔 γ ^ = 1 \hat\gamma=1 γ^=1。
假设待求解的权值为 ( w , b ) (\boldsymbol w,b) (w,b), 样本 x \boldsymbol x x 到 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 的几何间隔为 γ ^ ∥ w ∥ \dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert} ∥w∥γ^
函数间隔 γ ^ = 1 \hat\gamma=1 γ^=1 时的几何间隔写为 1 ∥ λ ′ w ∥ \dfrac{1}{\Vert\lambda^{\prime}\boldsymbol w\Vert} ∥λ′w∥1,也就是 ( w , b ) (\boldsymbol w,b) (w,b) 缩放为了 ( λ ′ w , λ ′ b ) , λ ′ = 1 / γ ^ (\lambda^{\prime}\boldsymbol w,\lambda^{\prime}b),\ \lambda^{\prime}=1/\hat\gamma (λ′w,λ′b), λ′=1/γ^
而 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0 和 λ ′ w T x + λ ′ b = 0 \lambda^{\prime}\boldsymbol w^T\boldsymbol x+\lambda^{\prime}b=0 λ′wTx+λ′b=0 是同一个分类面
\qquad 那么,约束最优化问题(2)就可以写为:
max w , b γ ^ ∥ w ∥ s . t . y i ( w T x i + b ) ≥ γ ^ , ∀ x i ⟹ γ ^ = 1 max w , b 1 ∥ w ∥ s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\textcolor{darkblue}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{\hat\gamma}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge \hat\gamma,\ \forall\ \boldsymbol x_i\end{aligned}}\quad\overset{\hat\gamma=1}\Longrightarrow\qquad\textcolor{royalblue}{\begin{aligned}&\max_{\boldsymbol w,b}\ \dfrac{1}{\Vert\boldsymbol w\Vert}\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\ \forall\ \boldsymbol x_i\end{aligned}} w,bmax ∥w∥γ^ s.t. yi(wTxi+b)≥γ^, ∀ xi⟹γ^=1w,bmax ∥w∥1 s.t. yi(wTxi+b)≥1, ∀ xi
\qquad
\qquad 又由于 max 1 ∥ w ∥ ⟺ min 1 2 ∥ w ∥ 2 \max\ \dfrac{1}{\Vert\boldsymbol w\Vert}\Longleftrightarrow\min\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2 max ∥w∥1⟺min 21∥w∥2,因此可以构造出一个凸二次规划问题
\qquad 约束最优化问题(3)
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\qquad\textcolor{indigo}{\begin{aligned}&\min_{\boldsymbol w,b}\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\quad \forall\ \boldsymbol x_i\end{aligned}} w,bmin 21∥w∥2 s.t. yi(wTxi+b)≥1,∀ xi
\qquad
3. 支持向量
\qquad 支持向量 ( support vector ) (\text{support\ vector}) (support vector) 是指距离分类面最近的训练样本(红色 + 点),两个(红色点线)超平面 w T x + b = 1 \boldsymbol w^T\boldsymbol x+b=1 wTx+b=1 和 w T x + b = − 1 \boldsymbol w^T\boldsymbol x+b=-1 wTx+b=−1 之间的距离,称为间隔 ( margin ) (\text{margin}) (margin)。
\qquad 
\qquad 考察该凸二次规划最优化问题:
min w , b 1 2 ∥ w ∥ 2 s . t . y i ( w T x i + b ) ≥ 1 , ∀ x i \qquad\qquad\qquad\begin{aligned}&\min_{\boldsymbol w,b}\ \dfrac{1}{2}\Vert\boldsymbol w\Vert^2\\ &\ s.t.\ \ \ y_i(\boldsymbol w^T\boldsymbol x_i+b) \ge 1,\quad \forall\ \boldsymbol x_i\end{aligned} w,bmin 21∥w∥2 s.t. yi(wTxi+b)≥1,∀ xi
\qquad 支持向量也是使得约束条件的等式成立的点,即: y ( w T x + b ) = 1 y(\boldsymbol w^T\boldsymbol x+b)=1 y(wTx+b)=1。在线性可分的情况下,选择不同的点作为支持向量,就可以确定不同的分离超平面 w T x + b = 0 \boldsymbol w^T\boldsymbol x+b=0 wTx+b=0。
- (正例的)支持向量 x i , y i = + 1 : y i ( w T x i + b ) = 1 ⇒ H 1 : w T x i + b = 1 \boldsymbol x_i,y_i=+1:\ y_i(\boldsymbol w^T\boldsymbol x_i+b)=1 \qquad\Rightarrow\quad H_1:\boldsymbol w^T\boldsymbol x_i+b=1 xi,yi=+1: yi(wTxi+b)=1⇒H1:wTxi+b=1
其余的 (正例的)训练样本满足 w T x i + b > 1 \boldsymbol w^T\boldsymbol x_i+b>1 wTxi+b>1- (负例的)支持向量 x j , y j = − 1 : y j ( w T x j + b ) = 1 ⇒ H 2 : w T x j + b = − 1 \boldsymbol x_j,y_j=-1:y_j(\boldsymbol w^T\boldsymbol x_j+b)=1 \qquad\Rightarrow\quad H_2:\boldsymbol w^T\boldsymbol x_j+b=-1 xj,yj=−1:yj(wTxj+b)=1⇒H2:wTxj+b=−1
其余的 (负例的)训练样本满足 w T x i + b < − 1 \boldsymbol w^T\boldsymbol x_i+b<-1 wTxi+b<−1- 两个超平面 H 1 H_1 H1 与 H 2 H_2 H2 之间的间隔为 2 ∥ w ∥ \dfrac{2}{\Vert\boldsymbol w\Vert} ∥w∥2
\qquad
\qquad
【写在最后】SVM的资料太多了,越写越觉得没什么特别的内容值得去写。攒在草稿箱里太久,发出来就当留个记录吧。
相关文章:

线性可分SVM摘记
线性可分SVM摘记 0. 线性可分1. 训练样本到分类面的距离2. 函数间隔和几何间隔、(硬)间隔最大化3. 支持向量 \qquad 线性可分的支持向量机是一种二分类模型,支持向量机通过核技巧可以成为非线性分类器。本文主要分析了线性可分的支持向量机模型,主要取自…...
LabVIEW在调用image.cpp或drawmgr.cpp因为DAbort而崩溃
LabVIEW在调用image.cpp或drawmgr.cpp因为DAbort而崩溃 出现下列问题,如何解决? 1. LabVIEW 程序因image.cpp或drawmgr.cpp中的错误而崩溃 2. 正在通过cRIO-9034运行独立的LabVIEW应用程序,但它因drawmgr.cpp中的错误而崩溃 …...
nodejs微信小程序+python+PHP贵州旅游系统的设计与实现-计算机毕业设计推荐MySQL
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

WebUI自动化学习(Selenium+Python+Pytest框架)003
1.元素操作 在成功定位到元素之后,我们需要对元素进行一些操作动作。常用的元素操作动作有: (1)send_keys() 键盘动作:向浏览器发送一个内容,通常用于输入框输入内容或向浏览器发送快捷键 (2…...

python+Appium自动化:python多线程多并发启动appium服务
Python启动Appium 服务 使用Dos命令或者bat批处理来手动启动appium服务,启动效率低下。如何将启动Appium服务也实现自动化呢? 这里需要使用subprocess模块,该模块可以创建新的进程,并且连接到进程的输入、输出、错误等管道信息&…...
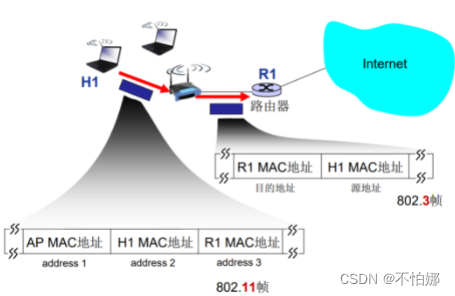
【计算机网络笔记】802.11无线局域网
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...

用C++和python混合编写数据采集程序?
之前看过一篇文章,主要阐述的就是多种语言混合编写爬虫程序,结合各种语言自身优势写一个爬虫代码是否行得通?觉得挺有意思的,带着这样的问题,我尝试着利用我毕生所学写了一段C和python混合爬虫程序,目前运行…...
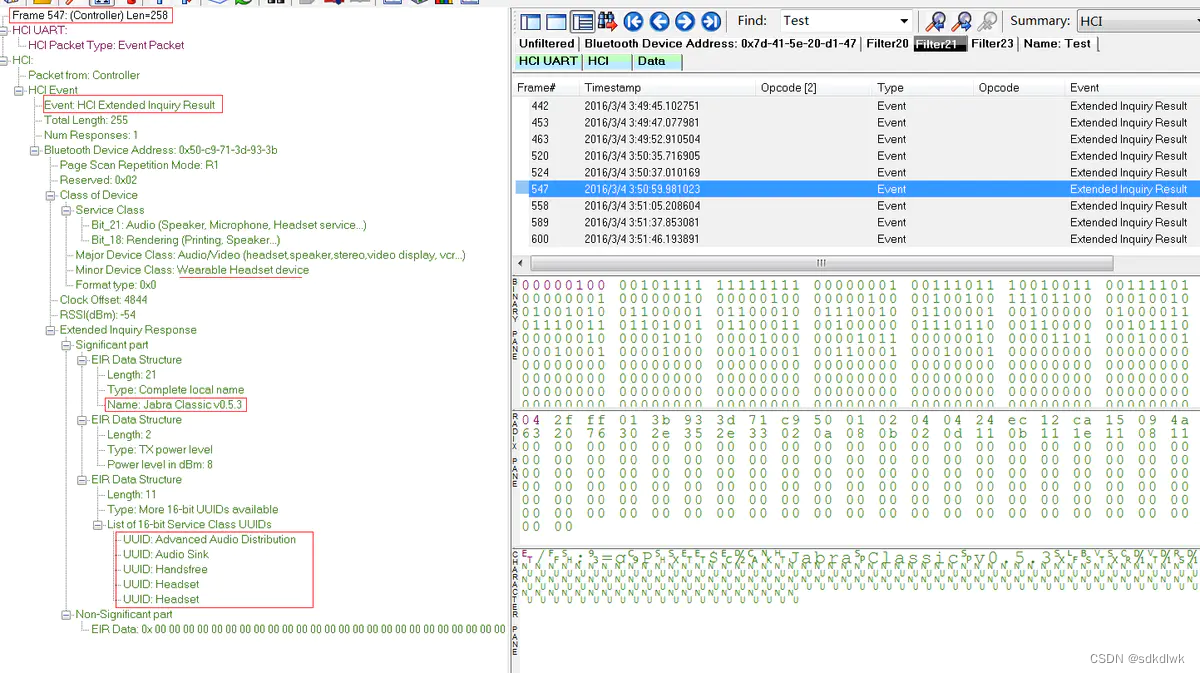
Android HCI日志分析案例1
案例1--蓝牙扫描设备过程分析 应用层发起搜索蓝牙设备,Android 官方提供的蓝牙扫描方式有三种,分别如下: BluetoothAdapter.startDiscovery(); //可以扫描经典蓝牙和BLE两种。BluetoothAdapter.startLeScan();//扫描低功耗蓝牙,…...
官方文档四:Prompts下——prompt templates的存储、加载、组合和部分格式化)
LangChain(0.0.339)官方文档四:Prompts下——prompt templates的存储、加载、组合和部分格式化
文章目录 一、 部分提示模板1.1 使用字符串值进行部分格式化(Partial with strings)1.2 使用函数进行部分格式化(Partial with functions) 二、Prompt pipelining2.1 String prompt pipelining2.2 Chat prompt pipelining 三、使用…...
鸿蒙开发笔记
最近比较火,本身也是做前端的,就抽空学习了下。对前端很友好 原视频地址:黑马b站鸿蒙OS视频 下载安装跟着视频或者文档就可以了。如果你电脑上安装的有node,但是开发工具显示你没安装,不用动咱们的node,直…...
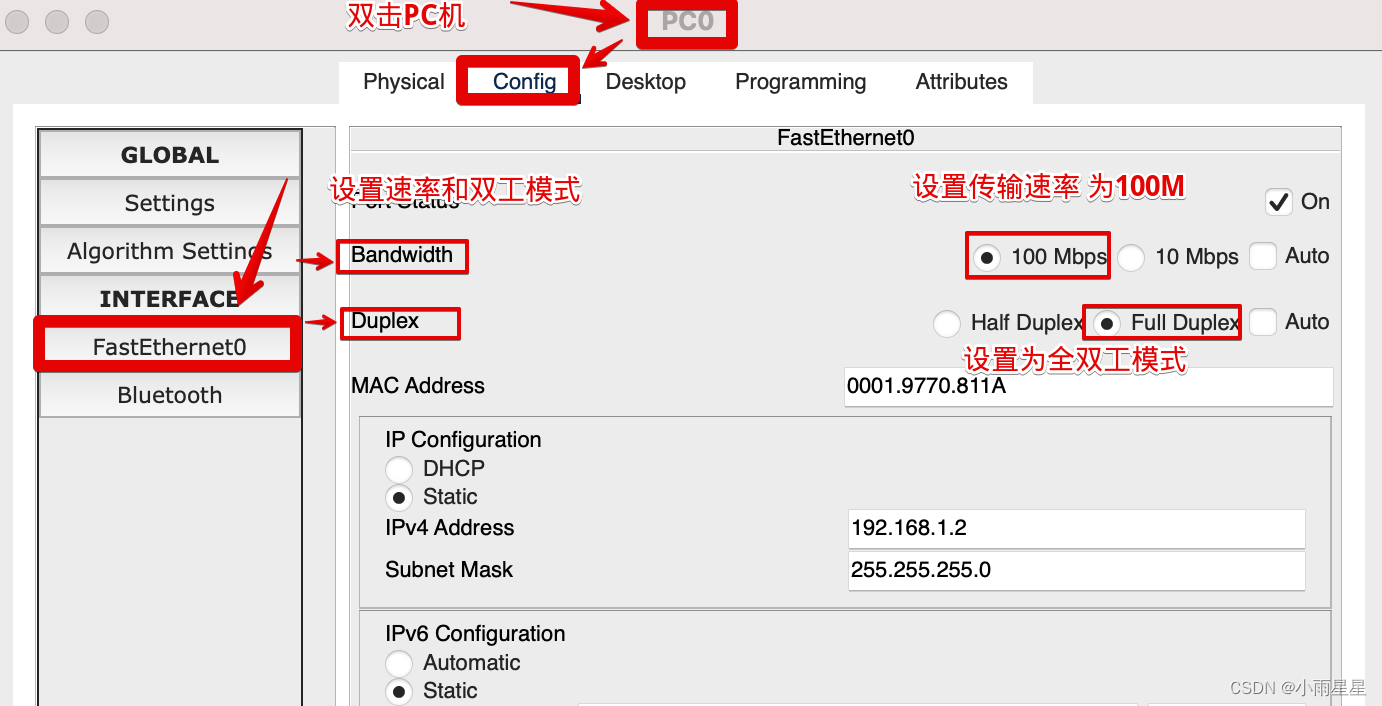
「计算机网络」Cisco Packet Tracker计算机网络仿真器的使用
介绍 Cisco Packet Tracker:网络仿真工具,用于模拟网络配置。 (一) 配置交换机(Switch)(通过 带外管理) 带外:Out-of-Band, OOB写在前面:如何打开Console页…...
:KeyboardInterrupt)
【已解决】if lock.acquire(block, timeout):KeyboardInterrupt
问题描述 Traceback (most recent call last): File "/media/visionx/monica/project/ResShift/app.py", line 134, in <module> demo.launch(shareFalse) File "/home/visionx/anaconda3/envs/ResShift/lib/python3.9/site-packages/gradio/bloc…...

将Excel中的数据导入shell脚本,并调用expect脚本
主脚本test.sh #!/bin/bash # 设置超时时间 set timeout 240 # 将 Excel 文件转换为 CSV 格式 # test.xlsx > temp.csv # 初始化一个二维数组 declare -A data # 逐行读取 CSV 文件,并将每个单元格的数据存储在二维数组中 row1 while IFS, read -r col1 col2 co…...

elementui el-table用span-method方法对相同的列名或行名进行合并
看到的一篇文章 同理 如果对第二列进行合并的话copy一下第一个方法,让值赋给第二个数组就可以 // 合并方法mergeCells({ row, column , rowIndex, columnIndex }) {debugger;if (columnIndex 1) {const _row this.spanArr[rowIndex];const _col _row > 0 ? …...
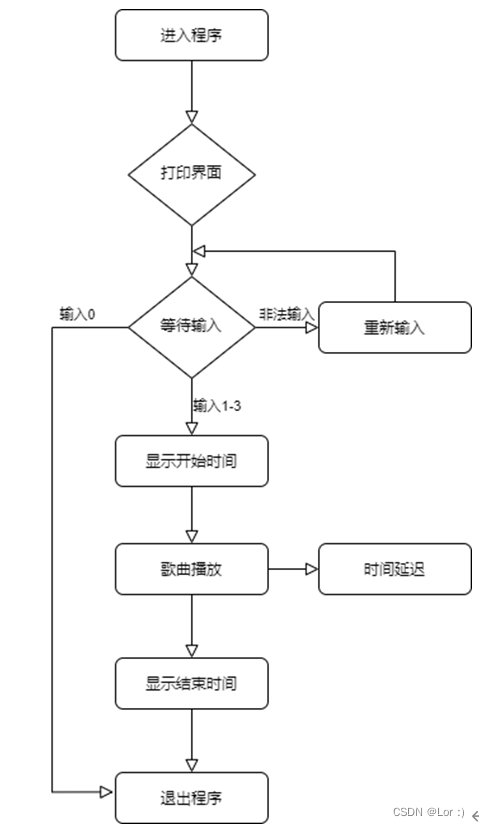
汇编语言实现音乐播放器
目标程序 用汇编语言实现一个音乐播放器,并支持点歌 Overview 乐曲是按照一定的高低、长短和强弱关系组成的音调,在一首乐曲中,每个音符的音高和音长与频率和节拍有关,因此我们要分别为3首要演奏的乐曲定义一个频率表和一个节拍…...
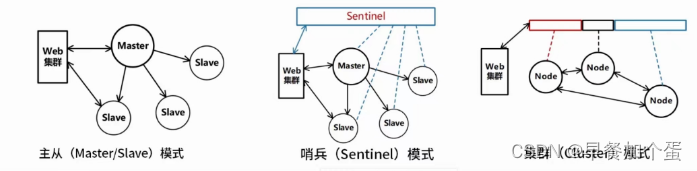
大型网站系统架构演化(Web)
大型网站系统架构演化 大型网站系统架构演化需要关注的维度涉及的技术演进过程单体架构垂直架构使用缓存改善网站性能缓存与数据库的数据一致性问题缓存技术对比Redis分布式存储方案Redis集群切片的常见方式Redis数据类型Redis 淘汰算法使用服务集群改善网站并发能力 大型网站系…...
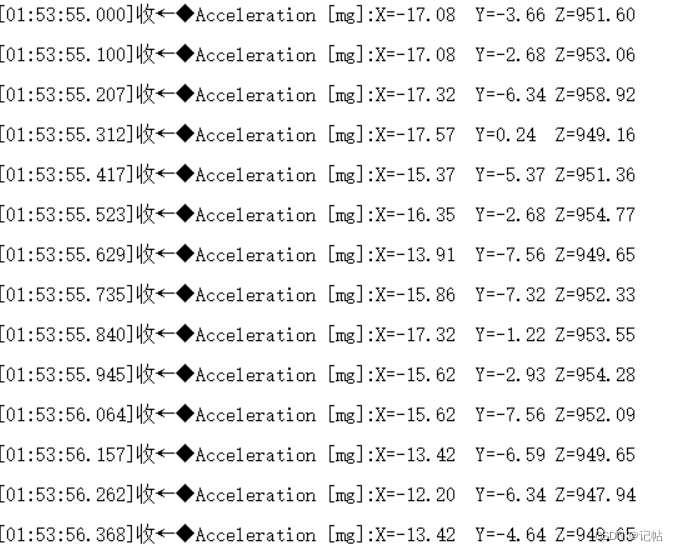
三轴加速度计LIS2DW12开发(2)----基于中断信号获取加速度数据
三轴加速度计LIS2DW12开发.2--轮基于中断信号获取加速度数据 概述视频教学样品申请生成STM32CUBEMX串口配置IIC配置CS和SA0设置INT1设置串口重定向参考程序初始换管脚获取ID复位操作BDU设置开启INT1中断设置传感器的量程配置过滤器链配置电源模式设置输出数据速率中断判断加速…...
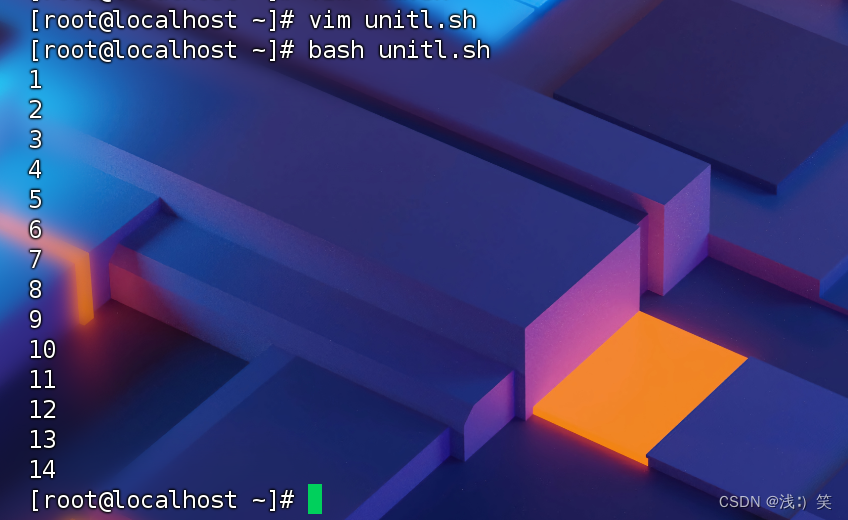
Shell循环:whileuntil
一、特点:循环次数[一定]是固定的 二、while语句结构 while 条件测试 do 循环体 done 当条件测试成立(条件测试为真),执行循环体 演示: 需求:每秒显示一个数字,一…...
Redis 安装部署
文章目录 1、前言2、安装部署2.1、单机模式2.1.1、通过 yum 安装(不推荐,版本老旧)2.1.1、通过源码编译安装(推荐) 2.2、主从模式2.3、哨兵模式2.4、集群模式2.5、其他命令2.6、其他操作系统 3、使用3.1、Java 代码 —…...
项目中遇到的半导体公司
作为一个技术人,我并不是亲美,从技术的实事求是角度讲,不得不感叹欧美的半导体技术。他们的datasheet能学到的东西太多太多;我甚至佩服他们缜密的逻辑。从他们的文章中领悟我们技术到底有多low,没办法一个一个了解所有…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
