动态规划学习——回文串
目录
一,回文子串
1.题目
2.题目接口
3,解题代码及其思路
解题代码:
二, 分割回文串II
1,题目
2,题目接口
3,解题思路及其代码
一,回文子串
1.题目
给你一个字符串
s,请你统计并返回这个字符串中 回文子串 的数目。回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc" 输出:3 解释:三个回文子串: "a", "b", "c"示例 2:
输入:s = "aaa" 输出:6 解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"提示:
1 <= s.length <= 1000s由小写英文字母组成
2.题目接口
class Solution {
public:int countSubstrings(string s) {}
};3,解题代码及其思路
在动态规划问题时一般可以分为五个步骤:
1.状态表示
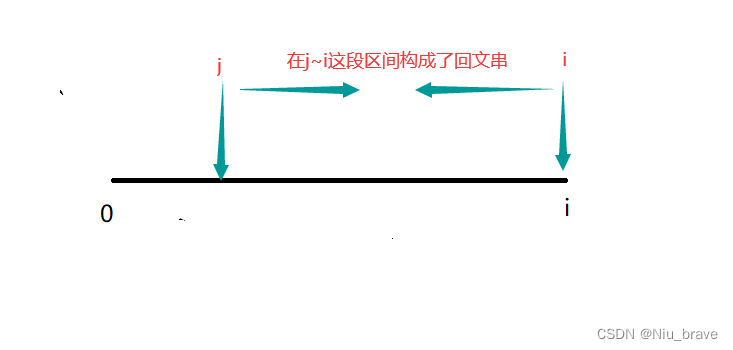
回文串问题我们一般以某一个区间为研究对象,所以我们可以使用bool dp[i][j]来表示i~j这段区间是否为回文串。
2.状态转移方程的推导
确定了状态转移方程以后,我们便可以来讨论状态转移方程。在推导状态转移方程时可以分为两种情况来推导:
1.s[i]==s[j],在这种情况下又可以分为三种情况来推导:
2.s[i]!=s[j]。在这种情况下dp[i][j]这段区间内的字符串肯定不是回文串。所以dp[i][j] = false。
3.填表顺序
因为在我们的状态转移方程内有dp[i][j] == dp[i+1][j-1]的情况,所以填表顺序为从下往上,从左往右。
4.初始化
在初始化的时候,要考虑的一个情况便是我的初始化要保证填表时不越界。dp[i][j] == do[i+1][j-1],在这种情况下因为 0<=i<=j<n。所以越界的情况在于i==n-1的时候,dp[i+1][j-1]会越界。但是我们要考虑这种情况吗?我们其实并不需要,因为j>=i,当i==j时会直接处理:dp[i][j] =true,并且只在这种情况下会越界。
5.返回值
在完成上面的工作以后,只需要完成对dp[i][j]中true情况的个数统计并返回。
解题代码:
class Solution { public:int countSubstrings(string s) {int n = s.size();//求字符串长度vector<vector<bool>>dp(n,vector<bool>(n));//建立n*n大小的dp表for(int i = n-1;i>=0;i--)//从下往上遍历{for(int j = i;j<n;j++)//从左到右遍历并且要保证j>=i{if(s[i] == s[j])//相等情况讨论{if(i == j) dp[i][j] = true;else if(j == i+1) dp[i][j] = true;else dp[i][j] = dp[i+1][j-1];}//s[i]!=s[j]时dp[i][j]绝对是false}}//统计回文子串个数int count = 0;for(int i = 0;i<n;i++){for(int j = i;j<n;j++){if(dp[i][j]) count++;}}return count;} };
二, 分割回文串II
1,题目
给你一个字符串
s,请你将s分割成一些子串,使每个子串都是回文。返回符合要求的 最少分割次数 。
示例 1:
输入:s = "aab" 输出:1 解释:只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。示例 2:
输入:s = "a" 输出:0示例 3:
输入:s = "ab" 输出:1提示:
1 <= s.length <= 2000s仅由小写英文字母组成
2,题目接口
class Solution {
public:int minCut(string s) {}
};3,解题思路及其代码
还是一样,按照之前的五个步骤:
1,状态方程:这次的状态转移方程表示的是分割回文串的最小次数。所以我们可以用一个线性的dp表来表示,用dp[i]表示0~i位置的最小切割次数。
2,状态转移方程:在确定好状态转移方程以后,我们就得来推导一下状态转移方程了。还是得分情况讨论:
在第一种情况下,因为0~i这个区间的字符可以构成回文串了所以dp[i] = 0。
在第二种情况下,需要在1~i这个区间内寻找一个能让dp[j][i]构成回文串的并且让切割次数最
最小:
在进行这一步以前还得分情况讨论:
状态转移方程代码如下:
for(int i = 0;i<n;i++){if(dp[0][i]){dp2[i] = 0;}else{for(int j =1;j<=i;j++){if(dp[j][i]) {dp2[i] = min(dp2[i],dp2[j-1]+1);}} }}3.初始化
因为我们要求的是最小值,所以我们在初始化时可以把状态表内的值初始化为一个特别大的值,这样便可以保证在我们填表时不会干扰到我们的在正确答案。
4,返回值
因为dp表代表的是到第i个位置的最小切割次数,所以我们的返回值就是dp[n-1]。
5,优化
因为在填表总是需要判断是否能构成回文串,所以我们可以采用判断回文子串的代码来对我们的代码做优化处理。
详细代码如下:
class Solution { public:int minCut(string s) {int n = s.size();//求字符串长度vector<vector<bool>>dp(n,vector<bool>(n));//建立n*n大小的dp表for(int i = n-1;i>=0;i--)//从下往上遍历{for(int j = i;j<n;j++)//从左到右遍历并且要保证j>=i{if(s[i] == s[j])//相等情况讨论{if(i == j) dp[i][j] = true;else if(j == i+1) dp[i][j] = true;else dp[i][j] = dp[i+1][j-1];}//s[i]!=s[j]时dp[i][j]绝对是false}}vector<int>dp2(n,0x7777777);//统计到第i个位置时的最小分割次数for(int i = 0;i<n;i++){if(dp[0][i]){dp2[i] = 0;}else{for(int j =1;j<=i;j++){if(dp[j][i]) {dp2[i] = min(dp2[i],dp2[j-1]+1);}} }}return dp2[n-1];} };
相关文章:

动态规划学习——回文串
目录 一,回文子串 1.题目 2.题目接口 3,解题代码及其思路 解题代码: 二, 分割回文串II 1,题目 2,题目接口 3,解题思路及其代码 一,回文子串 1.题目 给你一个字符串 s &…...

优化你的计算机性能:如何根据 CPU 占用率决定硬件升级
优化你的计算机性能:如何根据 CPU 占用率决定硬件升级 一、引言二、CPU 占用率的意义与影响三、监测和评估 CPU 占用率四、判断硬件升级需求的依据五、硬件升级方案和建议六、总结 一、引言 计算机性能优化是提升计算机系统整体效能的过程,它对于用户和…...
探索低代码之路——JNPF
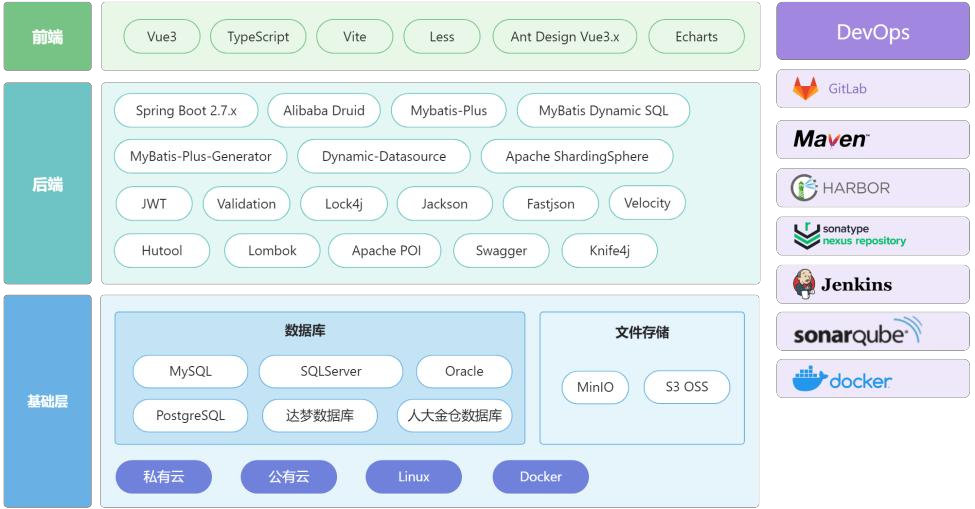
目录 一、低代码行业现状 二、产品分析 1.可视化应用开发 2.流程管理 3.整个平台源码合作 三、架构和技术 技术栈 四、规划和展望 低代码平台(Low-code Development Platform)是一种让开发者通过拖拽和配置,而非传统的手动编写大量代…...

Day01 嵌入式 -----流水灯
一、简单介绍 嵌入式系统中的流水灯是一种常见的示例项目,通常用于演示嵌入式系统的基本功能和控制能力。流水灯由多个发光二极管(LED)组成,这些LED按照一定的顺序依次点亮和熄灭,形成一种像水流一样的流动效果。 二、…...

Redis集群详解
1.1 什么是Redis集群 Redis集群是一种通过将多个Redis节点连接在一起以实现高可用性、数据分片和负载均衡的技术。它允许Redis在不同节点上同时提供服务,提高整体性能和可靠性。根据搭建的方式和集群的特性,Redis集群主要有三种模式:主从复制…...

【随笔】个人面试纪录
面试被问了几个问题。 1.mount怎么用 没答上来,说的 --help 可以看 mount --help | less mount [ --source ] <source> | [ --target ] <target> 2.ansible怎么用,有哪些常用的模块 ansible <hosts|all> -m <module> 常用的模块…...

Vue3的reactive、ref、toRef、toRefs用法以及区别
在 Vue3 中,reactive, ref, toRef, toRefs 都是用于创建响应式数据的方法。它们之间的主要区别在于它们的使用方式和返回值类型。 reactive:用于将一个普通对象转换为响应式对象。当对象的属性发生变化时,视图会自动更新。 import { reacti…...

微信小程序:input双向绑定
微信小程序:input双向绑定 微信小程序:input双向绑定1 数据容器准备2 输入组件准备3 逻辑代码准备4 总结实战示例1.wxml文件导入2.js文件导入 微信小程序:input双向绑定 <说明> PS:该笔记采用渐进式编程,使每一步…...
RT-Thread ADC_DMA
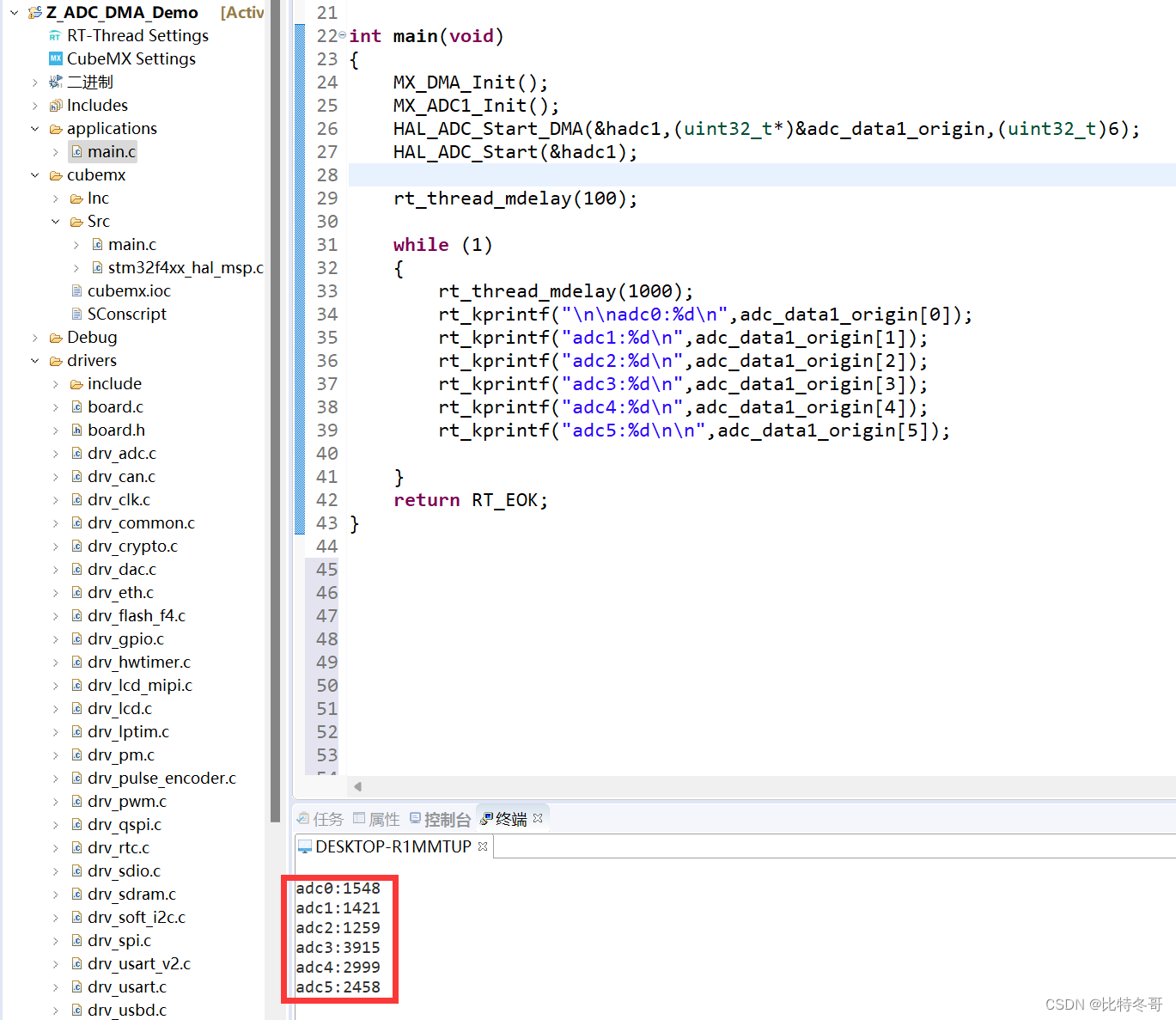
看到这里,相信大家已经尝试过网上各类ADC_DMA传输的文章,且大多都并不能实现,因为在RT-Thread中并没有找到关于ADC的DMA接口,在官方例程中有关DMA的传输也只有一个串口接收的介绍,找遍全网怕也没能找到真正有用的消息。…...
生成带依赖Jar 包的两种常用方式:IDEA打包工具:Artifacts 和 maven-shade-plugin
文章目录 前言1、IDEA打包工具:Artifacts1.1 创建Artifacts1.2 选择第三方jar文件1.3 打包Artifacts1.4 测试jar包 2、maven-shade-plugin2.1、pom文件添加2.2、打包2.3、测试jar包 总结 前言 当我们编写完Java程序后,为了提高执行效率通常会将应用程序…...

idea 插件开发日志绑定问题
错误日志 Searchable options index builder completed SLF4J: Class path contains multiple SLF4J bindings. SLF4J: Found binding in [jar:file:/D:/gradle/caches/modules-2/files-2.1/com.jetbrains.intellij.idea/ideaIC/2021.2/b0727ceddea2b62b16825db9308e14a470198…...
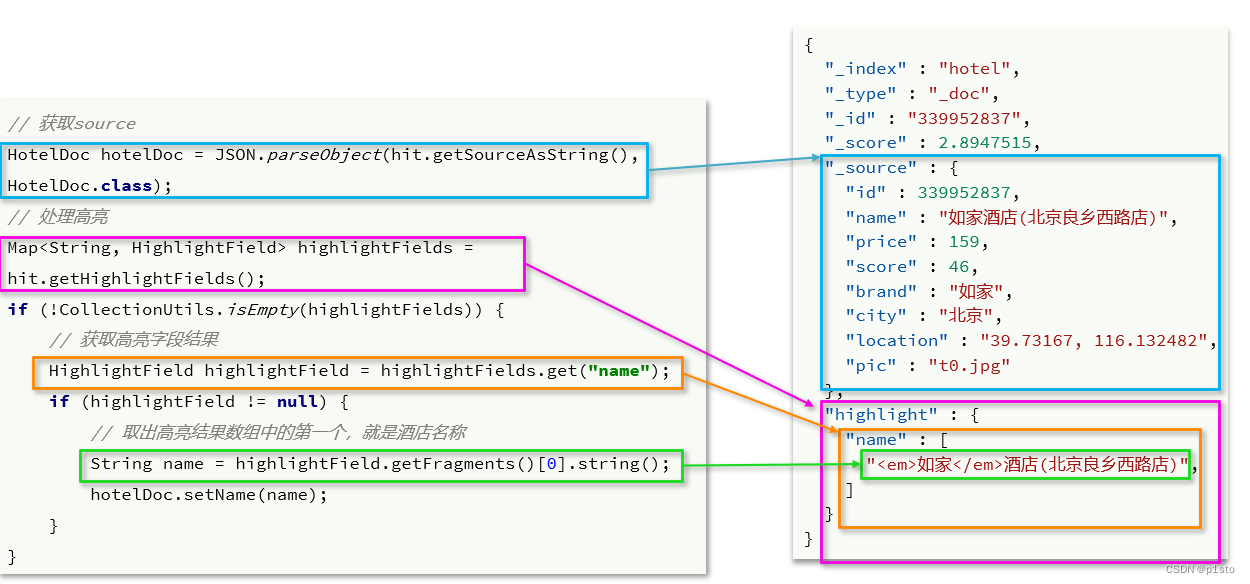
Elasticsearch(ES)概述
文章目录 一.什么是Elasticsearch?1.正向索引和倒排索引2.Mysql和ES的概念对比3.安装elasticsearch、kibana 二.IK分词器三.索引库操作四.文档操作五.RestClient操作索引库1.初始化RestClient2.创建索引库3.删除索引库4.判断索引库是否存在 六.RestClient操作文档1.新增文档2.…...

网络入门---网络编程初步认识和实践
目录标题 前言准备工作udpserver.hpp成员变量构造函数初始化函数(socket,bind)start函数(recvfrom) udpServer.ccudpClient.hpp构造函数初始化函数run函数(sendto) udpClient.cc测试 前言 在上一篇文章中我们初步的认识了端口号的作用,ip地址和MAC地址在网络通信时…...
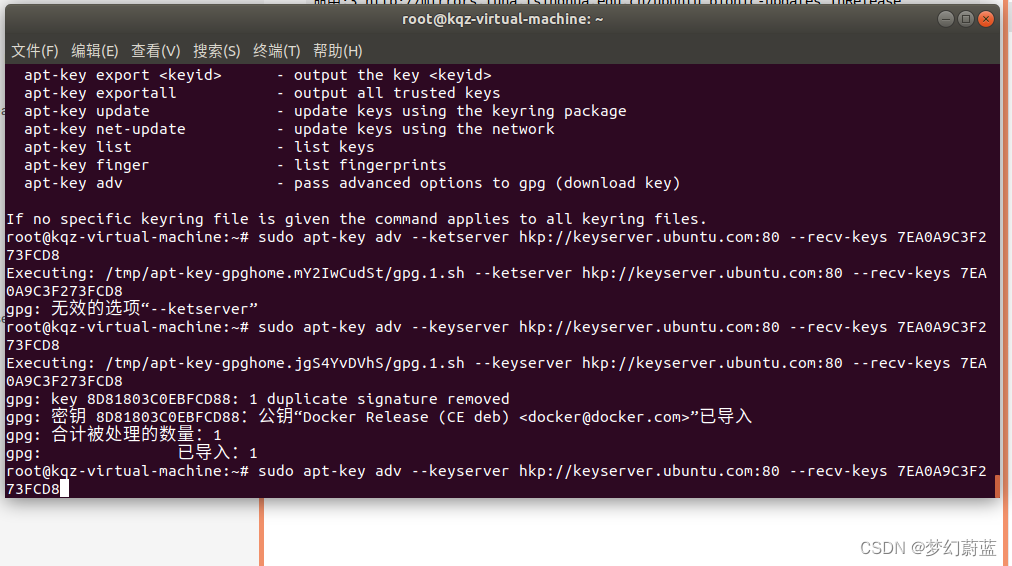
Linux系统安装Docker-根据官方教程教程(以Ubuntu为例)
Linux系统安装Docker-根据官方教程教程(以Ubuntu为例) 1. 背景介绍2. 环境配置2.1 软件环境要求2.2 软件下载2.3 文档地址2.3 必备命令工具下载 3. 安装Docker3.1 使用root用户操作后续命令3.2 卸载可能存在的旧版本 4. 安装Docker4.1 更新依赖包4.2 配置…...

2023-12-03 LeetCode每日一题(可获得的最大点数)
2023-12-03每日一题 一、题目编号 1423. 可获得的最大点数二、题目链接 点击跳转到题目位置 三、题目描述 几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。 每次行动,你可以从行的开头或者末尾拿一张卡牌&#x…...

【唐山海德教育】安全员b证的考试科目
安全员b证考试内容包括对安全生产知识和管理能力考核,采用书面或计算机闭卷考试方式,内容包括安全生产法律法规、安全管理和安全技术等内容。其中,法律法规占50%,安全管理占40%,土建综合安全技术占6%,机械设…...
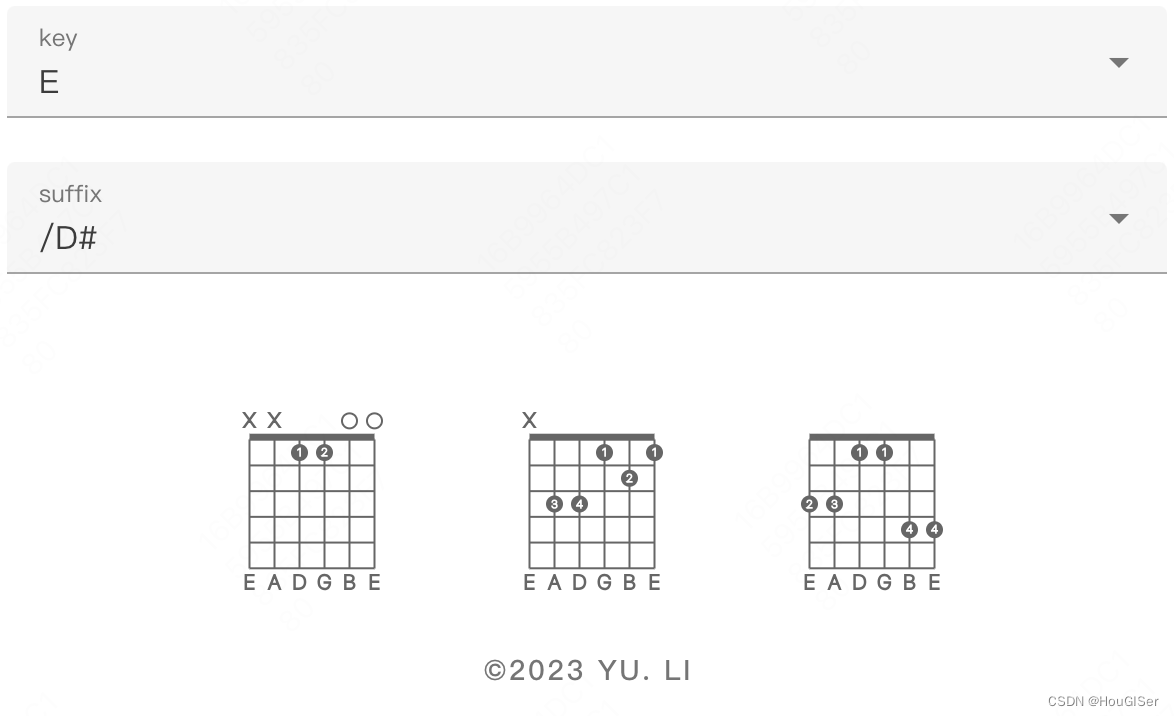
吉他初学者学习网站搭建系列(4)——如何查询和弦图
文章目录 背景实现ChordDbvexchords 背景 作为吉他初学者,如何根据和弦名快速查到和弦图是一个必不可少的功能。以往也许你会去翻和弦的书籍查询,像查新华字典那样,但是有了互联网后我们不必那样,只需要在网页上输入和弦名&#…...

九章量子计算机:探索量子世界的革命性工具
九章量子计算机:探索量子世界的革命性工具 一、引言 九章量子计算机的推出,是近年来科技界最为引人瞩目的成就之一。这款基于量子力学的计算机,以其独特的计算方式和潜在的应用前景,引发了全球范围内的关注和讨论。本文将深入探讨九章量子计算机的原理、技术特点、应用前景…...

在 Linux 上修改 Oracle 控制文件、日志文件和数据文件的目录的脚本
以下是一个交互式的 Bash 脚本示例,用于在 Linux 上修改 Oracle 数据库控制文件、日志文件和数据文件的目录。脚本会要求您输入要修改的路径,并根据输入的路径执行相应的修改操作。 #!/bin/bash# 修改以下变量以匹配您的 Oracle 数据库设置 ORACLE_SID&…...
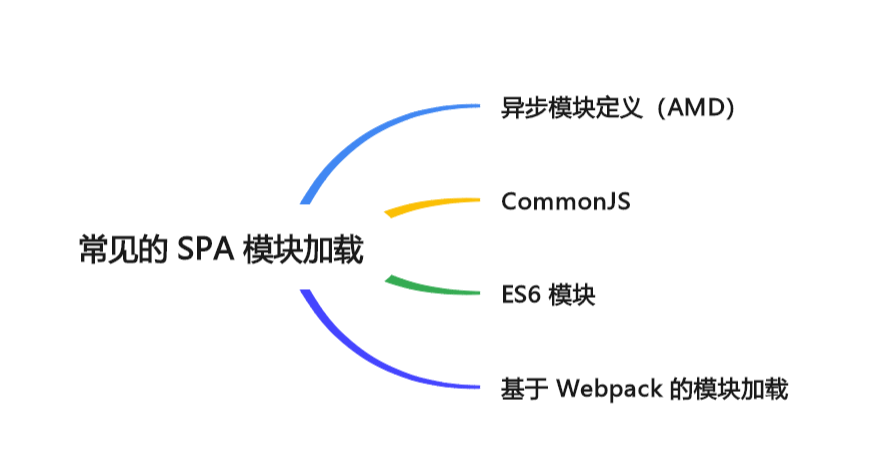
JavaScript 延迟加载的艺术:按需加载的最佳实践
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...