【算法专题】二分查找
二分查找
- 二分查找
- 1. 二分查找
- 2. 在排序数组中查找元素的第一和最后一个位置
- 3. 搜索插入位置
- 4. x 的平方根
- 5. 山脉数组的峰顶索引
- 6. 寻找峰值
- 7. 寻找旋转排序数组中的最小值
- 8. 点名
二分查找
1. 二分查找
题目链接 -> Leetcode -704.二分查找
Leetcode -704.二分查找
题目:给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 - 1。
示例 1:
输入: nums = [-1, 0, 3, 5, 9, 12], target = 9
输出 : 4
解释 : 9 出现在 nums 中并且下标为 4
示例 2 :
输入 : nums = [-1, 0, 3, 5, 9, 12], target = 2
输出 : -1
解释 : 2 不存在 nums 中因此返回 - 1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在[1, 10000]之间。
nums 的每个元素都将在[-9999, 9999]之间。
思路:
-
定义 left , right 指针,分别指向数组的左右区间。
-
找到待查找区间的中间点 mid ,找到之后分三种情况讨论:
- arr[mid] == target 说明正好找到,返回 mid 的值;
- arr[mid] > target 说明 [mid, right] 这段区间都是大于 target 的,因此舍去右边区间,在左边 [left, mid -1] 的区间继续查找,即让 right = mid - 1 ,然后重复 2 过程;
- arr[mid] < target 说明 [left, mid] 这段区间的值都是小于 target 的,因此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid + 1 ,然后重复 2 过程;
- 当 left 与 right 错开时,说明整个区间都没有这个数,返回 -1 。
代码如下:
class Solution {public:int search(vector<int>& nums, int target){int left = 0, right = nums.size() - 1;while (left <= right){int mid = left + (right - left) / 2; // 防止溢出if (nums[mid] > target) right = mid - 1; // 中间数比 target 大,改变右指针else if (nums[mid] < target) left = mid + 1; // 中间数比 target 小,改变左指针else return mid; // 找到返回下标}return -1;}};
2. 在排序数组中查找元素的第一和最后一个位置
题目链接 -> Leetcode -34.在排序数组中查找元素的第一和最后一个位置
Leetcode -34.在排序数组中查找元素的第一和最后一个位置
题目:给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回[-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5, 7, 7, 8, 8, 10], target = 8
输出:[3, 4]
示例 2:
输入:nums = [5, 7, 7, 8, 8, 10], target = 6
输出:[-1, -1]
示例 3:
输入:nums = [], target = 0
输出:[-1, -1]
提示:
- 0 <= nums.length <= 10^5
- 10^9 <= nums[i] <= 10^9
nums 是一个非递减数组 - 10^9 <= target <= 10^9
思路:二分思想,就是根据数据的性质,在某种判断条件下将区间一分为二,然后舍去其中一个区间,然后再另一个区间内查找;为了方便叙述,用 x 表示该元素, resLeft 表示左边界, resRight 表示右边界;
寻找左边界思路:
我们注意到以左边界划分的两个区间的特点:
- 左边区间 [left, resLeft - 1] 都是小于 x 的;
- 右边区间(包括左边界) [resLeft, right] 都是大于等于 x 的;
因此,关于 mid 的落点,我们可以分为下面两种情况:
- 当我们的 mid 落在 [left, resLeft - 1] 区间的时候,也就是 arr[mid] < target 。说明 [left, mid] 都是可以舍去的,此时更新 left 到 mid + 1 的位置,继续在 [mid + 1, right] 上寻找左边界;
- 当 mid 落在 [resLeft, right] 的区间的时候,也就是 arr[mid] >= target 。说明 [mid + 1, right] (因为 mid 可能是最终结果,不能舍去)是可以舍去的,此时更新 right 到 mid 的位置,继续在 [left, mid] 上寻找左边界;
注意:这里找中间元素需要向下取整。因为后续移动左右指针的时候:
- 左指针: left = mid + 1 ,是会向后移动的,因此区间是会缩小的;
- 右指针: right = mid ,可能会原地踏步(比如:如果向上取整的话,如果剩下 1,2 两个元素, left == 1 , right == 2 , mid == 2 。更新区间之后, left,right,mid 的值没有改变,就会陷入死循环)。因此一定要注意,当 right = mid 的时候,要向下取整。
同理大家可以尝试分析寻找右边界的思路。
代码如下:
class Solution {public:vector<int> searchRange(vector<int>& nums, int target){if (nums.size() == 0) return { -1, -1 };int left = 0, right = nums.size() - 1;int begin = -1;// 寻找左端点while (left < right){// 当元素个数为偶数个时,取左边的为中间元素,因为要找的是左边界int mid = left + (right - left) / 2; if (nums[mid] < target) left = mid + 1;else right = mid;}if (target == nums[left]) begin = left;else return { -1, -1 };left = 0, right = nums.size() - 1;// 寻找右端点while (left < right){// 当元素个数为偶数个时,取右边的为中间元素,因为要找的是右边界// 或者当更新 right / left 时出现 -1 取mid的时候就要+1int mid = left + (right - left + 1) / 2; if (nums[mid] > target) right = mid - 1;else left = mid;}return { begin, right };}};
3. 搜索插入位置
题目链接 -> Leetcode -35.搜索插入位置
Leetcode -35.搜索插入位置
题目:给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1, 3, 5, 6], target = 5
输出 : 2
示例 2 :
输入 : nums = [1, 3, 5, 6], target = 2
输出 : 1
示例 3 :
输入 : nums = [1, 3, 5, 6], target = 7
输出 : 4
提示 :
- 1 <= nums.length <= 10^4
- 10^4 <= nums[i] <= 10^4
nums 为 无重复元素 的 升序 排列数组 - 10^4 <= target <= 10^4
思路与上题思路类似,寻找目标值的左边界即可。
代码如下:
class Solution {public:int searchInsert(vector<int>& nums, int target){// 如果插入的位置在最后if (nums[nums.size() - 1] < target) return nums.size();int left = 0, right = nums.size() - 1;// 二分查找找左边界while (left < right){int mid = left + (right - left) / 2;if (nums[mid] < target) left = mid + 1;else right = mid;}return left;}};
4. x 的平方根
题目链接 -> Leetcode -69.x 的平方根
Leetcode -69.x 的平方根
题目:给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31 - 1
思路也和上题类似,寻找右边界即可;
代码如下:
class Solution {public:int mySqrt(int x){// long long 防止溢出long long left = 0, right = x;// 二分查找寻找右边界while (left < right){long long mid = left + (right - left + 1) / 2;if (mid * mid > x) right = mid - 1;else left = mid;}return left;}};
5. 山脉数组的峰顶索引
题目链接 -> Leetcode -825.山脉数组的峰顶索引
Leetcode -825.山脉数组的峰顶索引
题目:符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3
存在 i(0 < i < arr.length - 1)使得:
arr[0] < arr[1] < … arr[i - 1] < arr[i]
arr[i] > arr[i + 1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
示例 1:
输入:arr = [0, 1, 0]
输出:1
示例 2:
输入:arr = [0, 2, 1, 0]
输出:1
示例 3:
输入:arr = [0, 10, 5, 2]
输出:1
提示:
3 <= arr.length <= 10^5
0 <= arr[i] <= 10^6
题目数据保证 arr 是一个山脉数组
思路:
- 分析峰顶位置的数据特点,以及山峰两旁的数据的特点:
- 峰顶数据特点: arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ;
- 峰顶左边的数据特点: arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ,也就是呈现上升趋势;
- 峰顶右边数据的特点: arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ,也就是呈现下降趋势。
- 因此,根据 mid 位置的信息,我们可以分为下面三种情况:
- 如果 mid 位置呈现上升趋势,说明我们接下来要在 [mid + 1, right] 区间继续搜索;
- 如果 mid 位置呈现下降趋势,说明我们接下来要在 [left, mid - 1] 区间搜索;
- 如果 mid 位置就是山峰,直接返回结果。
代码如下:
class Solution {public:int peakIndexInMountainArray(vector<int>& arr) {int left = 0,right = arr.size() - 1;// 符合二段性,就可以用二分查找while(left < right){int mid = left + (right - left + 1)/2;if(arr[mid] > arr[mid - 1]) left = mid;else right = mid - 1;}return left;}};
6. 寻找峰值
题目链接 -> Leetcode -162.寻找峰值
Leetcode -162.寻找峰值
题目:峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1, 2, 3, 1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1, 2, 1, 3, 5, 6, 4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
- 1 <= nums.length <= 1000
- 2^31 <= nums[i] <= 2^31 - 1
- 对于所有有效的 i 都有 nums[i] != nums[i + 1]
思路:寻找二段性:
任取⼀个点 i ,与下一个点 i + 1 ,会有如下两种情况:
- arr[i] > arr[i + 1] :此时「左侧区域」一定会存在山峰(因为最左侧是负无穷,但此时还没有下降趋势),那么我们可以去左侧去寻找结果;
- arr[i] < arr[i + 1] :此时「右侧区域」一定会存在山峰(因为最右侧是负无穷,但此时还没有下降趋势),那么我们可以去右侧去寻找结果。
当我们找到「二段性」的时候,就可以尝试用「二分查找」算法来解决问题。
代码如下:
class Solution {public:int findPeakElement(vector<int>& nums) {int left = 0, right = nums.size() - 1;// 符合二段性,可以用二分查找while(left < right){int mid = left + (right - left)/2;if(nums[mid] > nums[mid + 1]) right = mid;else left = mid + 1;}return left;}};
7. 寻找旋转排序数组中的最小值
题目链接 -> Leetcode -153.寻找旋转排序数组中的最小值
Leetcode -153.寻找旋转排序数组中的最小值
题目:已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0, 1, 2, 4, 5, 6, 7] 在变化后可能得到:
若旋转 4 次,则可以得到[4, 5, 6, 7, 0, 1, 2]
若旋转 7 次,则可以得到[0, 1, 2, 4, 5, 6, 7]
注意,数组[a[0], a[1], a[2], …, a[n - 1]] 旋转一次 的结果为数组[a[n - 1], a[0], a[1], a[2], …, a[n - 2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3, 4, 5, 1, 2]
输出:1
解释:原数组为[1, 2, 3, 4, 5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4, 5, 6, 7, 0, 1, 2]
输出:0
解释:原数组为[0, 1, 2, 4, 5, 6, 7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11, 13, 15, 17]
输出:11
解释:原数组为[11, 13, 15, 17] ,旋转 4 次得到输入数组。
提示:
- n == nums.length
- 1 <= n <= 5000
- 5000 <= nums[i] <= 5000
nums 中的所有整数 互不相同
nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
思路:题目中的数组规则如下图所示:
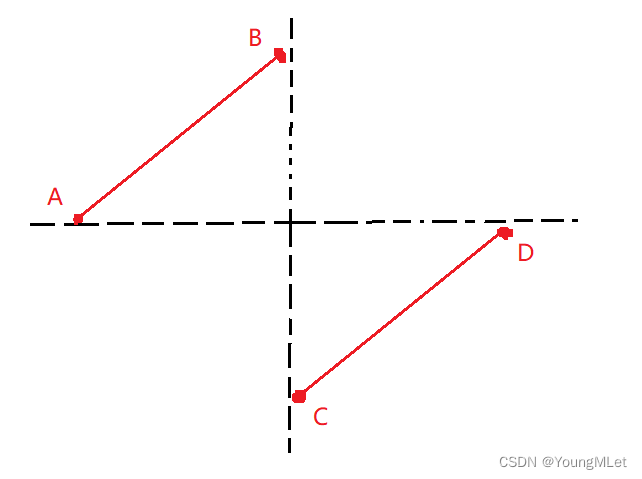
其中 C 点就是我们要求的点。
二分的本质:找到一个判断标准,使得查找区间能够一分为二。
通过图像我们可以发现, [A,B] 区间内的点都是严格大于 D 点的值的, C 点的值是严格小于 D 点的值的。但是当 [C,D] 区间只有一个元素的时候, C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left , right :
然后根据 mid 的落点,我们可以这样划分下一次查询的区间:
- 当 mid 在 [A,B] 区间的时候,也就是 mid 位置的值严格大于 D 点的值,下一次查询区间在 [mid + 1,right] 上;
- 当 mid 在 [C,D] 区间的时候,也就是 mid 位置的值严格小于等于 D 点的值,下次查询区间在 [left,mid] 上。
当区间长度变成 1 的时候,就是我们要找的结果。
代码如下:
class Solution {public:int findMin(vector<int>& nums) {int left = 0, right = nums.size() - 1;while(left < right){// 以最右边的元素为目标进行比较int mid = left + (right - left )/2;if(nums[mid] > nums[nums.size() - 1]) left = mid + 1;else right = mid;}return nums[left];}};
8. 点名
题目链接 -> Leetcode -LCR 173.点名
Leetcode -LCR 173.点名
题目:某班级 n 位同学的学号为 0 ~n - 1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0, 1, 2, 3, 5]
输出 : 4
示例 2 :
输入 : records = [0, 1, 2, 3, 4, 5, 6, 8]
输出 : 7
提示:
1 <= records.length <= 10000
思路是以数组下标为目标对象进行比较,寻找左边界即可;
代码如下:
class Solution {public:int missingNumber(vector<int>& nums) {int left = 0, right = nums.size() - 1;while(left < right){// 以数组下标为目标对象进行比较int mid = left + (right - left)/2;if(nums[mid] > mid) right = mid;else left = mid + 1;}return left == nums[left]? left + 1 : left;}};
相关文章:

【算法专题】二分查找
二分查找 二分查找1. 二分查找2. 在排序数组中查找元素的第一和最后一个位置3. 搜索插入位置4. x 的平方根5. 山脉数组的峰顶索引6. 寻找峰值7. 寻找旋转排序数组中的最小值8. 点名 二分查找 1. 二分查找 题目链接 -> Leetcode -704.二分查找 Leetcode -704.二分查找 题…...

中国消费电子行业发展趋势及消费者需求洞察|徐礼昭
一、引言 近年来,随着科技的飞速发展,消费电子行业面临着前所未有的挑战与机遇。本文将从行业发展趋势、消费者需求洞察以及企业数字化转型的方向和动作三个方面,对消费电子行业进行深入剖析。 二、消费电子行业发展趋势 5G技术的普及和应…...
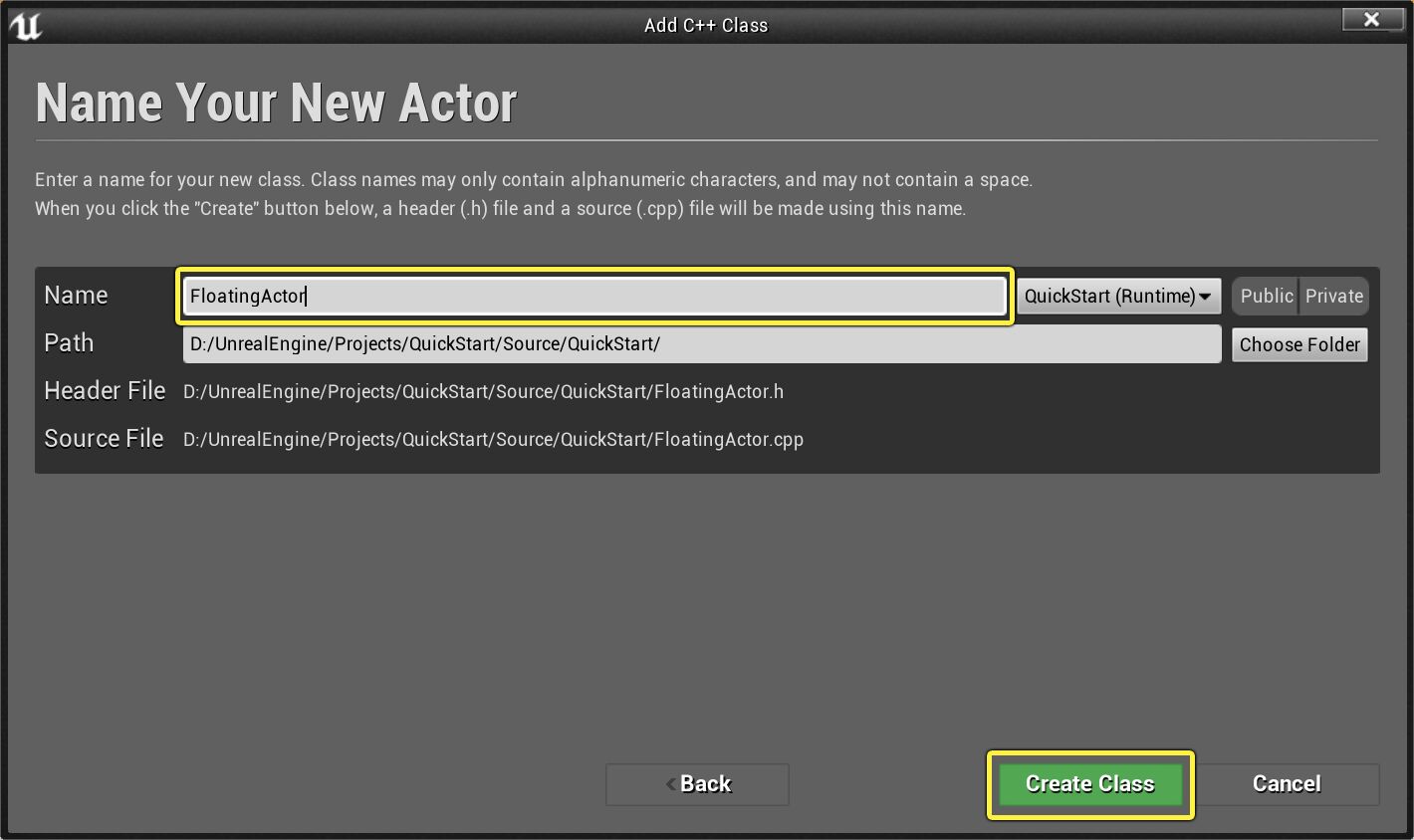
UE学习C++(1)创建actor
创建新C类 在 虚幻编辑器 中,点击 文件(File) 下拉菜单,然后选择 新建C类...(New C Class...) 命令: 此时将显示 选择父类(Choose Parent Class) 菜单。可以选择要扩展的…...

【CTA认证】Android8实现android6以下的应用运行时也要申请权限
需求 CTA入网认证,要求低版本比如Android6以下的应用,运行时,也需要有运行时权限(Runtime Permission)功能,不能默认就取到权限,必须人工在设置中打开才可。 环境 Android 8 实现 frameworks 修改思路是所有APP都…...

gRPC Java、Go、PHP使用例子
文章目录 1、Protocol Buffers定义接口1.1、编写接口服务1.2、Protobuf基础数据类型 2、服务器端实现2.1、生成gRPC服务类2.2、Java服务器端实现 3、java、go、php客户端实现3.1、Java客户端实现3.2、Go客户端实现3.3、PHP客户端实现 本文例子是在Window平台测试,Ja…...
———px,em,rem,vw,vh之间的区别)
前端知识笔记(十九)———px,em,rem,vw,vh之间的区别
一,px(像素):像素是屏幕上显示的最小单位,它是固定的,不随页面缩放而改变大小。在响应式设计中,使用像素单位可能会导致布局在不同屏幕尺寸上显示不一致。例如:现在在你电脑上一个字…...
docker部署frp穿透内网
文章目录 (1)部署frps服务器(2)部署frpc客户端(3)重启与访问frp(4)配置nginx反向代理 (1)部署frps服务器 docker安装参考文档:docker基本知识 1…...

使用pytorch从零开始实现迷你GPT
生成式建模知识回顾: [1] 生成式建模概述 [2] Transformer I,Transformer II [3] 变分自编码器 [4] 生成对抗网络,高级生成对抗网络 I,高级生成对抗网络 II [5] 自回归模型 [6] 归一化流模型 [7] 基于能量的模型 [8] 扩散模型 I, 扩散模型 II…...

tp6框架 万级数据入库 php函数优化
将万级数据入库并判断有无 没有则新增 上篇是用mysql的replace into实现 本篇是另一种方法 这是我的数据格式: $data [ [ KCH > value1, other_column1 > value_other1_1, other_column2 > value_other2_1, ], [ KCH > value2, other_column…...
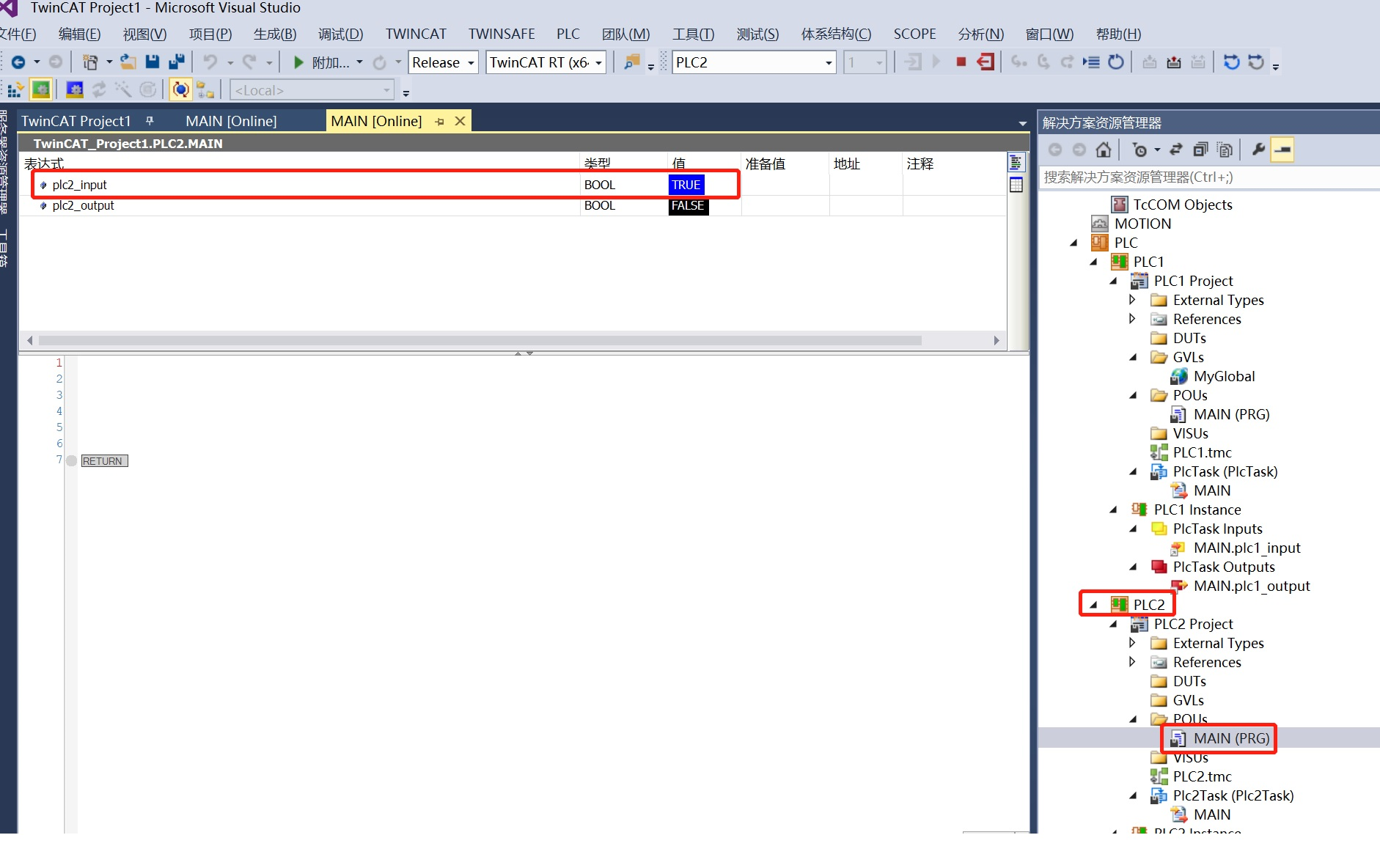
TwinCAT3一个PLC设备里多个程序工程之间通讯
目录 1、创建TwinCAT3工程,再分别创建两个PLC程序工程 2、PLC1工程中添加如下代码,然后编译重新生成PLC1工程 3、PLC2工程中添加如下代码,然后编译重新生成PLC2工程 4、变量关联 5、一个PLC运行多个PLC工程设置 7、工程下载链接 1、创建…...
python弹球小游戏
import pygame import random# 游戏窗口大小 WIDTH 800 HEIGHT 600# 定义颜色 WHITE (255, 255, 255) BLACK (0, 0, 0) RED (255, 0, 0) GREEN (0, 255, 0) BLUE (0, 0, 255)# 球的类 class Ball:def __init__(self):self.radius 10self.speed [random.randint(2, 4),…...
mongoose学习记录
mongoose安装和连接数据库 npm i mongoose导入mongoose const mongoose require(mongoose) mongoose.set("strictQuery",true)连接数据库 mongoose.connect(mongodb:127.0.0.1:27017/test)设置回调 mongoose.connection.on(open,()>{console.log("连接成…...

边缘与云或边缘加云:前进的方向是什么?
边缘计算使数据处理更接近数据源,以及由此产生的行动或决策的对象。通过设计,它可以改变数十亿物联网和其他设备存储、处理、分析和通信数据的方式。 边缘计算使数据处理更接近数据源,以及由此产生的行动或决策的对象。这与传统的体系结构形成…...

蓝桥杯第1037题子串分值和 C++ 字符串 逆向思维 巧解
题目 思路和解题方法 方案一——遍历哈希表 仅能过60%样例,大多数同学都用的该方法,就不过多赘述 #include <iostream> #include <unordered_map> using namespace std; int main() {string s;cin >> s;int n s.size();int res n;for (int i 0…...

力扣题:字符串的反转-11.23
力扣题-11.23 [力扣刷题攻略] Re:从零开始的力扣刷题生活 力扣题1:557. 反转字符串中的单词 III 解题思想:先读取单词,然后将单词进行翻转即可 class Solution(object):def reverseWords(self, s):""":type s…...

【软件测试】盘一盘工作中遇到的 Redis 异常测试
在测试工作中,涉及到与 redis 交互的场景变的越来越多了。关于redis本身就不作赘述了,网上随便搜,本人也做过一些整理。 今天只来复盘一下,在测试过程中与 redis 的二三事儿。其中提到的案例是经过抽象化的,用作辅助说…...

14.Oracle中RegExp_Like 正则表达式基本用法
--基本用法,是否包含某字符串 like %36% select * from k_micfo where regexp_like(loginid,36);if regexp_like(str,^[0-9\.]$) --只包含数字0-9,,小数点.--oracle判断字段是否是纯数字 (四种写法结果一样) select * from k_micfo where r…...
Docker Swarm总结+Jenkins安装配置与集成(5/5)
博主介绍:Java领域优质创作者,博客之星城市赛道TOP20、专注于前端流行技术框架、Java后端技术领域、项目实战运维以及GIS地理信息领域。 🍅文末获取源码下载地址🍅 👇🏻 精彩专栏推荐订阅👇🏻…...
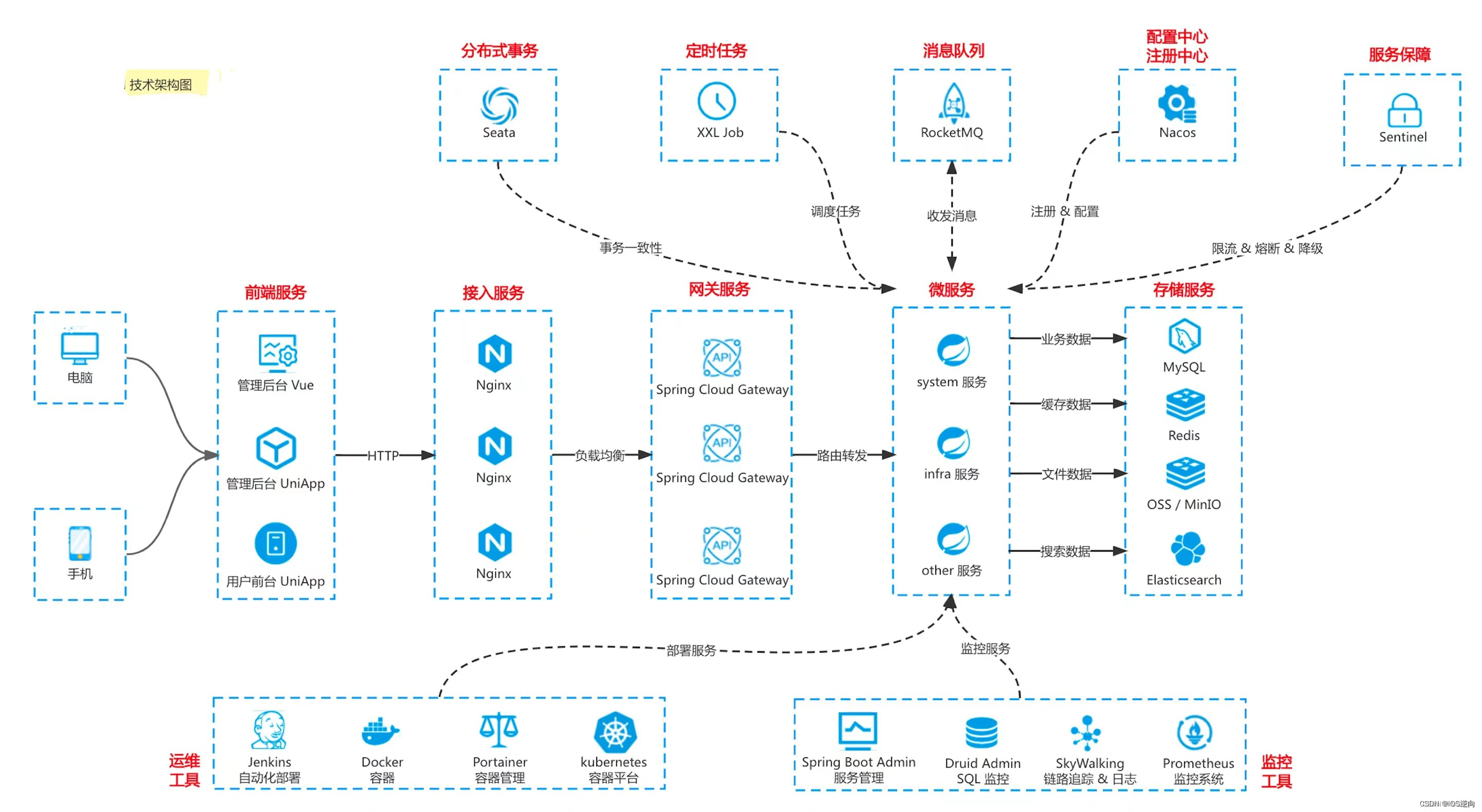
docker安装Sentinel zipkin
文章目录 引言I Sentinel安装1.1 运行容器1.2 DOCKERFILE 参考1.3 pom 依赖1.4 .yml配置(整合springboot)II 资源保护2.1 Feign整合Sentinel2.2 CommonExceptionAdvice:限流异常处理类III zipkin引言 消息服务和请求第三方服务可不配置Sentinel。 </...

利用python实现文件压缩打包的功能
主要是利用了zipfile实现文件压缩打包,简单实例代码如下: import zipfilewith zipfile.ZipFile("archive.zip",w) as zipf:zipf.write("config.ini")zipf.write("test.py") 其中的模式 w表示如果没有该文件则创建该文件…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
