图论|684.冗余连接 685. 冗余连接 II
684.冗余连接
题目:树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
题目链接:684.冗余连接
代码如下:
修改join函数
class Solution {public int[] father;public int[] findRedundantConnection(int[][] edges) {//构造并查集 过程中两个边根一样则删除int n=edges.length;father=new int[n+1];//初始化for(int i=1;i<=n;i++){father[i]=i;}int[] result=null;boolean flag;for(int j=0;j<edges.length;j++){flag=join(edges[j][0],edges[j][1]);if(flag==true){return new int[]{edges[j][0],edges[j][1]};}}return result;}public int find(int u){if(u==father[u]) return u;else return find(father[u]);}boolean join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return true;father[v] = u;return false;}
}
685. 冗余连接 II (再分析)
题目: 在本问题中,有根树指满足以下条件的 有向 图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。
输入一个有向图,该图由一个有着 n 个节点(节点值不重复,从 1 到 n)的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi],用以表示 有向 图中连接顶点 ui 和顶点 vi 的边,其中 ui 是 vi 的一个父节点。
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案
题目链接: 685. 冗余连接 II
解题思路:
先判断入度 删除入度为2的边的一条 判断删除后是不是树即可
再使用并查集判断是否有环(是否有冲突 此时的冲突一定是构成环)
如何使用并查集判断删除后是不是树
因为如果两个点所在的边在添加图之前如果就可以在并查集里找到了相同的根,那么这条边添加上之后 这个图一定不是树了
如何使用并查集判断判断是否有环(有环时 附加的边指向根节点)
附加的边指向根节点,而且是在环路中的最后一条被访问到的边
class Solution {private static final int N = 1010; // 如题:二维数组大小的在3到1000范围内private int[] father;public Solution() {father = new int[N];// 并查集初始化for (int i = 0; i < N; ++i) {father[i] = i;}}// 并查集里寻根的过程private int find(int u) {if(u == father[u]) {return u;}father[u] = find(father[u]);return father[u];}// 将v->u 这条边加入并查集private void join(int u, int v) {u = find(u);v = find(v);if (u == v) return ;father[v] = u;}// 判断 u 和 v是否找到同一个根,本题用不上private Boolean same(int u, int v) {u = find(u);v = find(v);return u == v;}/*** 初始化并查集*/private void initFather() {// 并查集初始化for (int i = 0; i < N; ++i) {father[i] = i;}}/*** 在有向图里找到删除的那条边,使其变成树* @param edges* @return 要删除的边*/private int[] getRemoveEdge(int[][] edges) {initFather();for(int i = 0; i < edges.length; i++) {if(same(edges[i][0], edges[i][1])) { // 构成有向环了,就是要删除的边return edges[i];}join(edges[i][0], edges[i][1]);}return null;}/*** 删一条边之后判断是不是树* @param edges* @param deleteEdge 要删除的边* @return true: 是树, false: 不是树*/private Boolean isTreeAfterRemoveEdge(int[][] edges, int deleteEdge){initFather();for(int i = 0; i < edges.length; i++){if(i == deleteEdge) continue;if(same(edges[i][0], edges[i][1])) { // 构成有向环了,一定不是树return false;}join(edges[i][0], edges[i][1]);}return true;}public int[] findRedundantDirectedConnection(int[][] edges) {int[] inDegree = new int[N];for(int i = 0; i < edges.length; i++){// 入度inDegree[ edges[i][1] ] += 1;}// 找入度为2的节点所对应的边,注意要倒序,因为优先返回最后出现在二维数组中的答案ArrayList<Integer> twoDegree = new ArrayList<Integer>();for(int i = edges.length - 1; i >= 0; i--){if(inDegree[edges[i][1]] == 2) {twoDegree.add(i);}}// 处理图中情况1 和 情况2// 如果有入度为2的节点,那么一定是两条边里删一个,看删哪个可以构成树if(!twoDegree.isEmpty()){if(isTreeAfterRemoveEdge(edges, twoDegree.get(0))) {return edges[ twoDegree.get(0)];}return edges[ twoDegree.get(1)];}// 明确没有入度为2的情况,那么一定有有向环,找到构成环的边返回就可以了return getRemoveEdge(edges);}
}
相关文章:

图论|684.冗余连接 685. 冗余连接 II
684.冗余连接 题目:树可以看成是一个连通且 无环 的 无向 图。 给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 …...
依据小兔鲜项目,总结Javascript数组常用方法
find 在向购物车添加某种规格的商品时,查找购物车列表中是否已经存在该规格的商品 find()方法传入一个回调函数,代表对数组每一项item的校验要求 返回数组中第一个符合条件的元素的值,如果没有则返回undefined const item cartList.value…...
制作飞腾(arm)芯片架构的nexus镜像
nexus官方没有arm架构的镜像,下面介绍一种自己制作镜像的方式 1、事先准备 在一个arm架构机器上安装docker下载nexus的linux版(https://www.sonatype.com/download-oss-sonatype)下载centos的arm架构镜像(docker pull centos-centos8.4.2105)下载arm版本的java8(ht…...

Git 标签管理
前言 标签 tag,就相当于对 某一次的 commit 做一个标识,起了一个别名,例如:在某个项目发布版本的时候,可针对最后一次 commit 起一个别名 v1.0 来标识这一次的commit。tag 的作用:commit id 相对于 tag 是很…...
多级缓存自用
1.什么是多级缓存 传统的缓存策略一般是请求到达Tomcat后,先查询Redis,如果未命中则查询数据库,如图: 存在下面的问题: •请求要经过Tomcat处理,Tomcat的性能成为整个系统的瓶颈 •Redis缓存失效时,会对数据库产生冲击 多级缓存就是充分利用请求处理的每个环节,添加缓…...
1.1卷积的作用
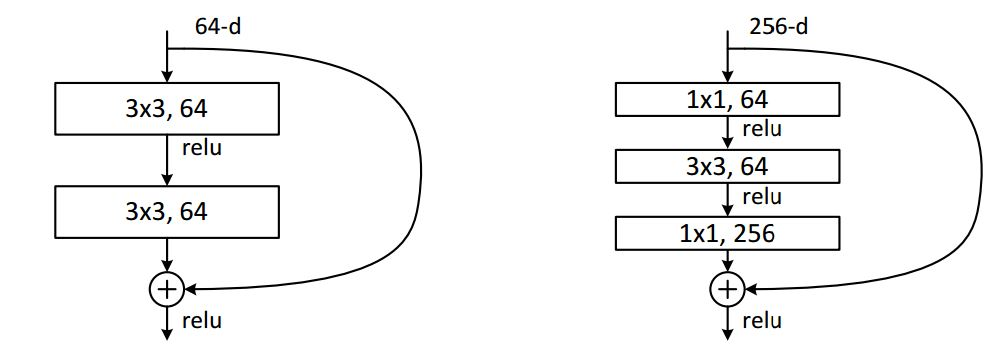
上图解释了1∗1卷积如何适用于尺寸为H∗W∗D的输入层,滤波器大小为1∗1∗D,输出通道的尺寸为H∗W∗1。如果应用n个这样的滤波器,然后组合在一起,得到的输出层大小为H∗W∗n。 1.1∗1卷积的作用 调节通道数 由于 11 卷积并不会改…...
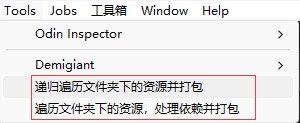
Unity 简单打包脚本
打包脚本 这个打包脚本适用于做demo,脚本放在Editor目录下 using System; using System.Collections; using System.Collections.Generic; using System.IO; using UnityEditor; using UnityEngine;public class BuildAB {[MenuItem("Tools/递归遍历文件夹下…...
基于社区电商的Redis缓存架构-缓存数据库双写、高并发场景下优化
基于社区电商的Redis缓存架构 首先来讲一下 Feed 流的含义: Feed 流指的是当我们进入 APP 之后,APP 要做一个 Feed 行为,即主动的在 APP 内提供各种各样的内容给我们 在电商 APP 首页,不停在首页向下拉,那么每次拉的…...

Python提取PDF表格(基于AUTOSAR_SWS_CANDriver.pdf)
个人学习笔记,仅供参考。 需求:提取AUTOSAR SWS中所有的API接口信息,用于生成C代码。 此处以AUTOSAR_SWS_CANDriver.pdf为例,若需要提取多个SWS文件,遍历各个文件即可。 1.Python包 pdfplumber是一款完全用python开…...
)
UVa1583生成元(Digit Generator)
题目 如果x加上x的各个数字之和得到y,也就是说x是y的生成元。给出n(1<n<100000),求最小生成元。无解则输出0。 输入输出样例 输入 3 216 121 2005输出 198 0 1979思路 要想解决这个题目,只需要对每一个输入的值从1开始遍历找到小于…...
【Springboot+vue】如何运行springboot+vue项目
从github 或者 gitee 下载源码后,解压,再从idea打开项目 后端代码处理 这是我在gitee下载下来的源码 打开之后,先处理后端代码 该配置的配置,该部署的部署 比如将sql文件导入数据库 然后去配置文件更改配置 然后启动项目 确保…...

拥抱变化,良心AI工具推荐
文章目录 💥 简介🍄 工具介绍🍓 功能特点🥗 使用场景🎉 用户体验🧩 下载地址🍭 总结 💥 简介 我是一名资深程序员,但薪资缺对不起资深两个字,为了生存&#x…...
Tensorflow的日志log记录
if OUTPUT_GRAPH:tf.summary.FileWriter("logs/", sess.graph)自动创建文件夹log...
C-语言每日刷题
目录 [蓝桥杯 2015 省 A] 饮料换购 题目描述 输入格式 输出格式 输入输出样例 # [蓝桥杯 2023 省 A] 平方差 题目描述 输入格式 输出格式 输入输出样例 说明/提示 【样例说明】 [NOIP2001 普及组] 数的计算 题目描述 输入格式 输出格式 输入输出样例 说明/提示 样例 1 解释 数据…...

十五届海峡两岸电视主持新秀大会竞赛流程
海峡两岸电视主持新秀会是两岸电视媒体共同举办的一项活动,旨在为两岸年轻的电视主持人提供一个展示才华的舞台,促进两岸文化交流和青年交流。本届新秀会是第十二届海峡两岸电视艺术节的重要活动之一。本次竞赛赛制流程如下: (1&…...

安全行业招聘信息汇总
1. 阿里巴巴-淘天集团-安全部 社招岗位:Java开发 招聘层级:P5-P6 工作年限:本科毕业1-3年,硕士毕业1-2年 base地点:杭州 职位描述 负责淘天安全部风控基础标签平台0到1能力建设及产品规划和落地。负责标签应用的产品…...

【如何学习python自动化测试】—— 浏览器驱动的安装 以及 如何更新driver
之前讲到基于python的自动化测试环境,需要安装Python,再安装Selenium。具体可看【如何学习Python自动化测试】—— 自动化测试环境搭建 但是,想要使用Selenium发送指令模拟人类行为操作浏览器,就需要安装浏览器驱动。不同的浏览器需要安…...

Spring Data Redis切换底层Jedis 和 Lettuce实现
1 简介 Spring Data Redis是 Spring Data 系列的一部分,它提供了Spring应用程序对Redis的轻松配置和使用。它不仅提供了对Redis操作的高级抽象,还支持Jedis和Lettuce两种连接方式。 可通过简单的配置就能连接Redis,并且可以切换Jedis和Lett…...

wireshark自定义协议插件开发
目录 脚本代码 报文显示 脚本代码 local NAME "test" test_proto Proto("test", "test Protocol") task_id ProtoField.uint16("test.task_id", "test id", base.DEC) cn ProtoField.uint8("test.cn", &qu…...

一文读懂MongoDB的全部知识点(1),惊呆面试官。
文章目录 01、mongodb是什么?02、mongodb有哪些特点?03、你说的NoSQL数据库是什么意思?NoSQL与RDBMS直接有什么区别?为什么要使用和不使用NoSQL数据库?说一说NoSQL数据库的几个优点?04、NoSQL数据库有哪些类型?05、M…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
