多元排列熵 Multivariate Permutation Entropy
熵(Entropy)
信息论中熵的概念首次被香农提出,目的是寻找一种高效/无损地编码信息的方法:以编码后数据的平均长度来衡量高效性,平均长度越小越高效;同时还需满足“无损”的条件,即编码后不能有原始信息的丢失。这样,香农提出了熵的定义:无损编码事件信息的最小平均编码长度。
香农信息熵 Shannon entropy
香农信息熵是由香农提出的一个概念,它描述了信息源各可能事件发生的不确定性。这个概念在信息论中扮演着重要的角色,解决了对信息的量化度量问题。
一条信息的信息量大小和它的不确定性有直接的关系。比如说,我们要搞清楚一件非常非常不确定的事,或是我们一无所知的事情,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。
信息量是对信息的度量,我们考虑一个离散的随机变量 x ,当我们观察到这个变量的具体值的时候,我们接收到了多少信息呢?
多少信息用信息量来衡量,我们接受到的信息量跟具体发生的事件有关。
信息的大小跟随机事件的概率有关。越小概率的事情发生了,产生的信息量越大,如湖南地震;越大概率的事情发生了产生的信息量越小,如太阳从东边升起来了(肯定发生, 没什么信息量)。
因此一个具体事件的信息量应该是随着其发生概率而递减的。
香农借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。
H ( x ) = − ∑ p ( x i ) l o g 2 ( p ( x i ) ) , i = 1 , 2 , . . , n H(x)=-∑p(x_i)log_2(p(x_i)),i=1,2,..,n H(x)=−∑p(xi)log2(p(xi)),i=1,2,..,n。
其中,x表示信息, x i ( i = 1 , 2 , . . , n ) x_i(i=1,2,..,n) xi(i=1,2,..,n)表示x的各种可能取值, p ( x i ) p(x_i) p(xi)表示x取值为 x i x_i xi的概率,H的单位是比特。这个公式可以用来计算信息的不确定性,即信息熵。信息熵的提出解决了对信息的量化度量问题。
香农熵在生物信息领域基因表达分析中也有广泛的应用,如一些或一个基因在不同组织材料中表达情况己知,但如何确定这些基因是组织特异性表达,还是广泛表达的,那我们就来计算这些基因在N个样本中的香农熵,结果越趋近于log2(N),则表明它是一个越广泛表达的基因,结果越趋近于0则表示它是一个特异表达的基因。
排列熵(Permutation Entropy)
是用于衡量时间序列复杂程度的指标
对于某个长度为n的排列x,其元素分别为 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn
-
规定一个嵌入维度m(即m-neighborhood)和时间延迟t,进行相空间重构
-
得到k个子序列, k = n − ( m − 1 ) t k=n-(m-1)t k=n−(m−1)t,每个子序列分别为:
(1) x 1 , x 1 + t , . . . , x 1 + ( m − 1 ) t x_1, x_{1+t}, ... , x_{1+(m-1)t} x1,x1+t,...,x1+(m−1)t
(2) x 2 , x 2 + t , . . . , x 2 + ( m − 1 ) t x_2, x_{2+t}, ... , x_{2+(m-1)t} x2,x2+t,...,x2+(m−1)t
(3) …
(4) x k , x k + t , . . . , x k + ( m − 1 ) t x_k, x_{k+t}, ... , x_{k+(m-1)t} xk,xk+t,...,xk+(m−1)t
-
并把其转换为大小关系的排列(k个,共有m!种可能性)
-
计算每种大小关系排列的概率P,P(排列)=该排列出现次数/k,
-
计算这些概率的信息熵
按照步骤举个例子,便于理解:
x={2,4,5,6,3,7,1},其长度n=7
-
设嵌入维度m=3(3-neightborhood),时间延迟t=1(没有skip)
-
得到k=n-(m-1)t=5个子序列,即:
(1) 2,4,5
(2) 4,5,6
(3) 5,6,3
(4) 6,3,7
(5) 3,7,1
- 转换为大小关系的排列,分别为:
(1) 1,2,3
(2) 1,2,3
(3) 2,3,1
(4) 2,1,3
(5) 2,3,1
- 以上排列共有3种,分别为2次(1,2,3),2次(2,3,1)和1次(2,1,3),这些排列的概率分别为:
(1) P(1,2,3) = 2/5
(2) P(2,3,1) = 2/5
(3) P(2,1,3) = 1/5
- 计算信息熵,得到 H p e ( 3 ) = 0.4 × l o g 2 2.5 + 0.4 × l o g 2 2.5 + 0.2 l o g 2 5 = 1.5219 Hpe(3)= 0.4×log_22.5 + 0.4×log_22.5 + 0.2log_25 = 1.5219 Hpe(3)=0.4×log22.5+0.4×log22.5+0.2log25=1.5219
排列熵作为衡量时间序列复杂程度的指标,越规则的时间序列,它对应的排列熵越小;越复杂的时间序列,它对应的排列熵越大。但是这样的结果是建立在合适的 m的选择的基础上的,如果 m 的选取很小,如1或者2的话,那么它的排列空间就会很小(1!、2!)。经过研究表明,这个 m 的选取还是要根据实际情况来决定,一般而言,Bandt and Pompe 建议的取值是m = 3 , . . . , 7
多元排列熵(Multivariate Permutation Entropy,MPE或MvPE)
多元排列熵(Multivariate Permutation Entropy,MPE或MvPE)是排列熵的扩展,由于 EEG 每个通道的数据并非独立,这样的扩展非常必要。
考虑EEG通道的时间窗口大小为T秒,其采样频率为 f s = 1 T f_s=\frac{1}{T} fs=T1;因此,每个窗口将包括 ( f s T ) (f_sT) (fsT)个样本,即数据点。
对于每个通道 i ∈ [ 1 , m ] i\in [1,m] i∈[1,m],每个 h ∈ [ 1 , n = d ! ] h\in [1,n=d!] h∈[1,n=d!](即对于每个“基序”),计数所有时间 s ∈ [ 1 , f s T − d ] s\in [1,f_sT−d] s∈[1,fsT−d],其中通道时间对 ( i , s ) (i,s) (i,s)提供基序j。
将计数除以mT后获得的频率 p i , j p_{i,j} pi,j是矩阵的项 P t ( m , n ) = p i , j P_t(m,n)={p_{i,j}} Pt(m,n)=pi,j,反映了基序在长度为T的时间片中的分布。
它保持 ∑ i = 1 m ∑ j = 1 d ! p i , j = 1 \sum ^m_{i=1}\sum ^{d!}_{j=1}p_{i,j}=1 ∑i=1m∑j=1d!pi,j=1。
根据该程序,原始多元时间序列被转换为一个时间相关矩阵,相关统计数据和可以容易地提取熵。
特别地,计算边际相对值很容易描述基序分布的频率,如:
p j = ∑ i = 1 m p i , j , j = 1 , . . . , d ! p_j=\sum ^m_{i=1}p_{i,j},j=1,...,d! pj=∑i=1mpi,j,j=1,...,d!,d表示多变量排列熵的跨通道复杂性可以是计算为 p j p_j pj的排列熵: H M P E ( s ) = − ∑ j = 1 d ! p j log 2 p j H_{MPE}(s)=-\sum_{j=1}^{d!} p_j\log_2p_j HMPE(s)=−∑j=1d!pjlog2pj
通过相同的矩阵,也可以计算单通道多元排列熵,如下所示:
H E ( i , s ) = − ∑ j = 1 d ! m p i , j log 2 ( m p i , j ) , i = 1 , 2 , . . . , m H_E(i,s)=-\sum_{j=1}^{d!} mp_{i,j}\log_2(mp_{i,j}),i=1,2,...,m HE(i,s)=−∑j=1d!mpi,jlog2(mpi,j),i=1,2,...,m
可计算出的一个有趣的量是多元排列熵和通过平均m个单通道排列熵得到的曲线之间的均方差。这个量被称为偶然性。当且仅当单通道分布重合时,它消失。如果它们是高度“相似”的,那么时间序列的整体复杂度有时是两项的总和:信道的平均复杂度和依赖于信道之间的不均匀性的休息。然而,对突发性对多元排列熵的影响的彻底分析超出了目前工作的范围。排列熵是一种对噪声(特别是高频噪声)稳健的测量方法:作为多元排列熵的平均操作实质上的轻微变化,它可以帮助吸收数据采集的一些不确定性。
多元排列熵在脑电图信号处理中很有用,因为如果它是在“遥远的”通道上计算的,即在不同的半球和/或不同的区域,它可以通过突出长期空间(非线性)相关性来提取跨通道的规律。
相关文章:

多元排列熵 Multivariate Permutation Entropy
熵(Entropy) 信息论中熵的概念首次被香农提出,目的是寻找一种高效/无损地编码信息的方法:以编码后数据的平均长度来衡量高效性,平均长度越小越高效;同时还需满足“无损”的条件,即编码后不能有原始信息的丢失。这样&a…...
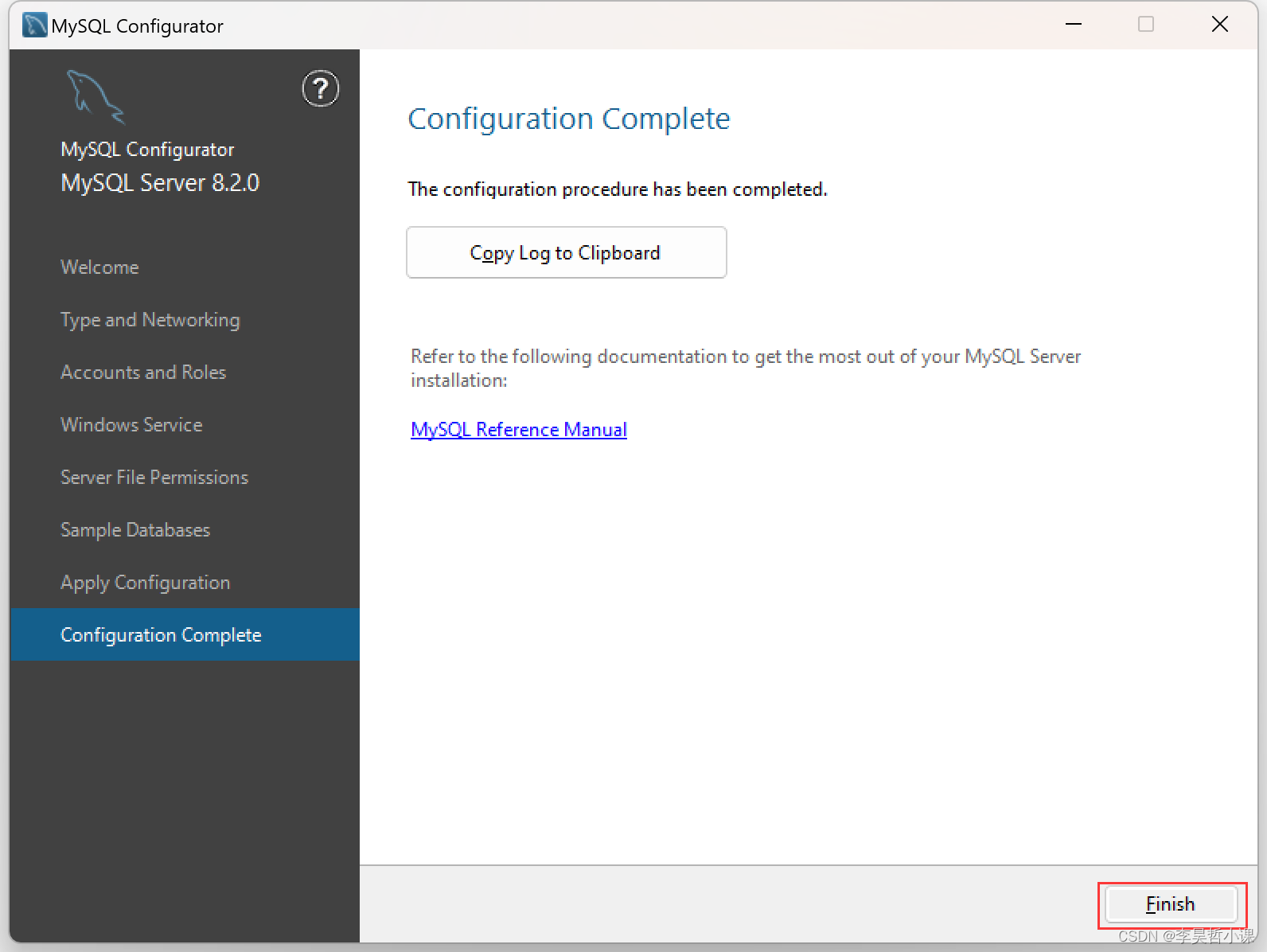
Windows安装MySQL8.2
Windows安装MySQL8.2 三种安装模式 默认自定义完整 本案例选择自定义 选择安装目录 勾选 Run MySQL Configurator 配置MYSQL 默认为开发者模式 在 Config Type 下拉列表中选择数据中心 设置 root 账号密码...
Windows下安全认证机制
NTLM(NT LAN Manager) NTLM协议是在Microsoft环境中使用的一种身份验证协议,它允许用户向服务器证明自己是谁(挑战(Chalenge)/响应(Response)认证机制),以便…...
(学习笔记)Xposed模块编写(一)
前提:需要已经安装Xposed Installer 1. 新建一个AS项目 并把MainActvity和activity_main.xml这两个文件删掉,然后在AndriodManifest.xml中去掉这个Activity的声明 2. 在settings.gralde文件中加上阿里云的仓库地址,否则Xposed依赖无法下载 m…...
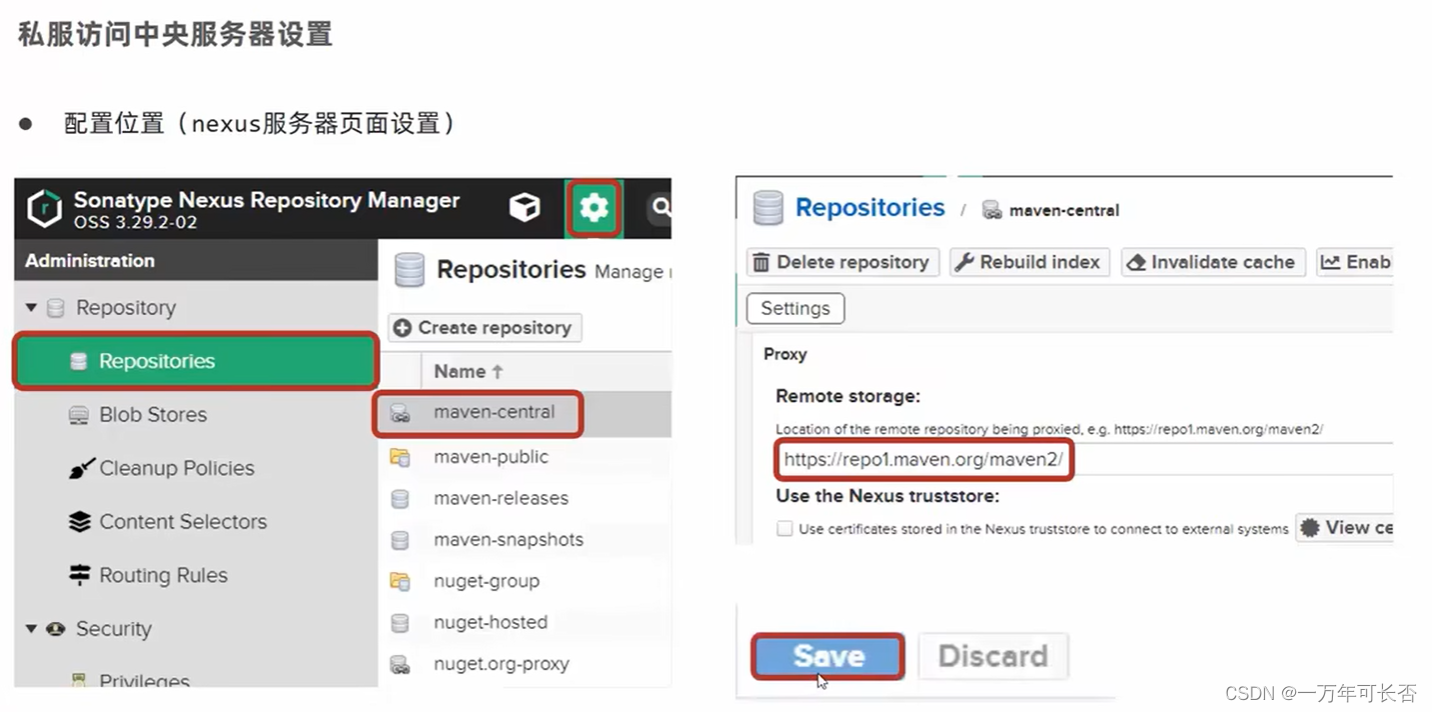
SSM框架(五):Maven进阶
文章目录 一、分模块开发1.1 分模块开发的意义1.2 步骤 二、依赖管理2.1 依赖传递2.2 可选依赖和排除依赖 三、继承与聚合3.1 聚合3.2 继承3.3 聚合和继承区别 四、属性4.1 pom文件的依赖使用属性4.2 资源文件使用属性 五、多环境开发六、跳过测试七、私服7.1 下载与使用7.2 私…...

【计算机视觉】基于OpenCV计算机视觉的摄像头测距技术设计与实现
基于计算机视觉的摄像头测距技术 文章目录 基于计算机视觉的摄像头测距技术导读引入技术实现原理技术实现细节Python-opencv实现方案获取目标轮廓步骤 1:图像处理步骤 2:找到轮廓步骤完整代码 计算图像距离前置技术背景与原理步骤 1:定义距离…...

Java项目实战《苍穹外卖》 四、Swagger接口文档
以铜为镜,可以正衣冠;以人为镜,可以明得失;以史为镜,可以知兴替。 - - - 李世民 系列文章目录 苍穹外卖是黑马程序员2023年的Java实战项目,作为业余练手用,需要源码或者课程的可以找我ÿ…...
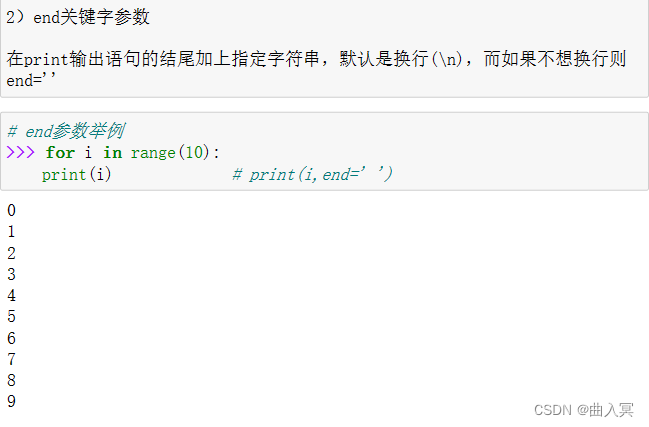
深度学习——第03章 Python程序设计语言(3.1 Python语言基础)
无论是在机器学习还是深度学习中,Python已经成为主导性的编程语言。而且,现在许多主流的深度学习框架,例如PyTorch、TensorFlow也都是基于Python。本课程主要是围绕“理论实战”同时进行,所以本章将重点介绍深度学习中Python的必备…...
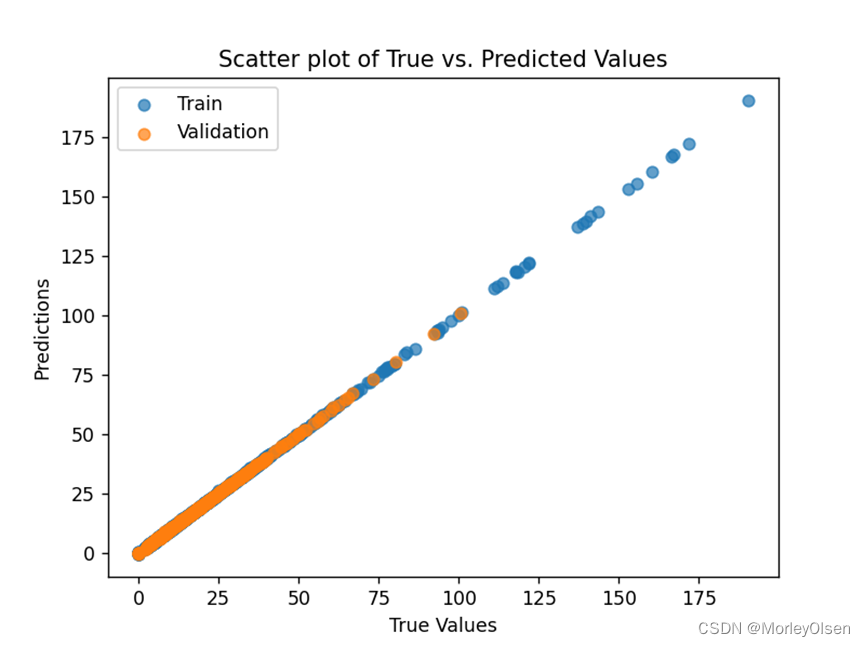
【人工智能Ⅰ】实验6:回归预测实验
实验6 回归预测实验 一、实验目的 1:了解机器学习中数据集的常用划分方法以及划分比例,并学习数据集划分后训练集、验证集及测试集的作用。 2:了解降维方法和回归模型的应用。 二、实验要求 数据集(LUCAS.SOIL_corr-实验6数据…...

前端下载文件的方法-blob下载
前端经常会遇到下载文件的需求,后端一般提供的以下两种方法: 文件地址。后端直接提供要下载的文件地址,常用于图片、音视频等静态文件文件流。后端返回文件流,常用于excel等动态文件 一、a 标签下载 1、直接html使用a标签下载 …...

zookeeper+kafka+ELK+filebeat集群
目录 一、zookeeper概述: 1、zookeeper工作机制: 2、zookeeper主要作用: 3、zookeeper特性: 4、zookeeper的应用场景: 5、领导者和追随者:zookeeper的选举机制 二、zookeeper安装部署: 三…...
-ChatGLM3)
【LangChain实战】开源模型学习(2)-ChatGLM3
介绍 ChatGLM3 是智谱AI和清华大学 KEG 实验室联合发布的新一代对话预训练模型。ChatGLM3-6B 是 ChatGLM3 系列中的开源模型,在保留了前两代模型对话流畅、部署门槛低等众多优秀特性的基础上,ChatGLM3-6B 引入了如下特性: 更强大的基础模型&a…...
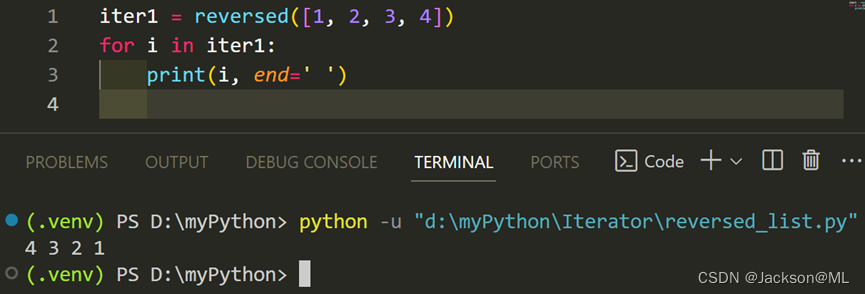
Python编程技巧 – 迭代器(Iterator)
Python编程技巧 – 迭代器(Iterator) By JacksonML Iterator(迭代器)是Python语言的核心概念之一。它常常与装饰器和生成器一道被人们提及,也是所有Python书籍需要涉及的部分。 本文简要介绍迭代器的功能以及实际的案例,希望对广大读者和学生有所帮助。…...

C语言练习题
C语言练习题 文章目录 C语言练习题题目一题目二题目三题目四题目五题目六题目八 题目一 #include <stdio.h> //VS2022,默认对齐数为8字节 union Un {short s[7];int n; };int main() {printf("%zd", sizeof(union Un));return 0; }代码运行结果:> 16 sizeo…...

常见的AI安全风险(数据投毒、后门攻击、对抗样本攻击、模型窃取攻击等)
文章目录 数据投毒(Data Poisoning)后门攻击(Backdoor Attacks)对抗样本攻击(Adversarial Examples)模型窃取攻击(Model Extraction Attacks)参考资料 数据投毒(Data Poi…...

flutter开发实战-为ListView去除Android滑动波纹
flutter开发实战-为ListView去除Android滑动波纹 在之前的flutter聊天界面上,由于使用ScrollBehavior时候,当时忘记试试了,今天再试代码发现不对。这里重新记录一下为ListView去除Android滑动波纹的方式。 一、ScrollBehavior ScrollBehav…...
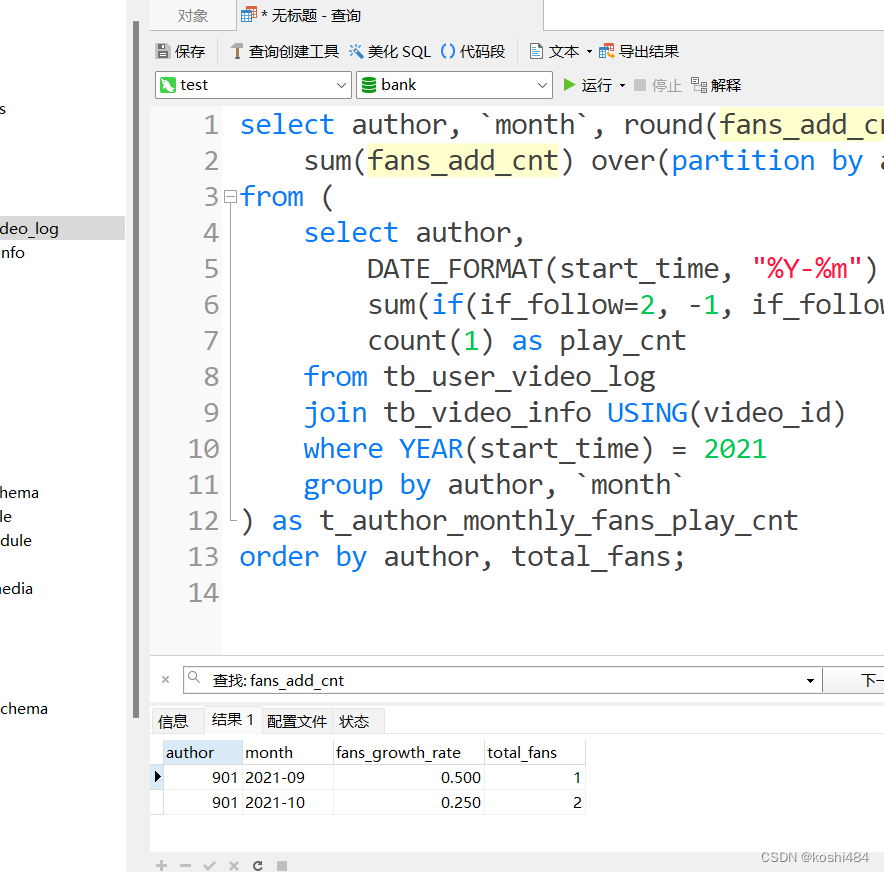
牛客在线编程(SQL大厂面试真题)
1.各个视频的平均完播率_牛客题霸_牛客网 ROP TABLE IF EXISTS tb_user_video_log, tb_video_info; CREATE TABLE tb_user_video_log (id INT PRIMARY KEY AUTO_INCREMENT COMMENT 自增ID,uid INT NOT NULL COMMENT 用户ID,video_id INT NOT NULL COMMENT 视频ID,start_time d…...
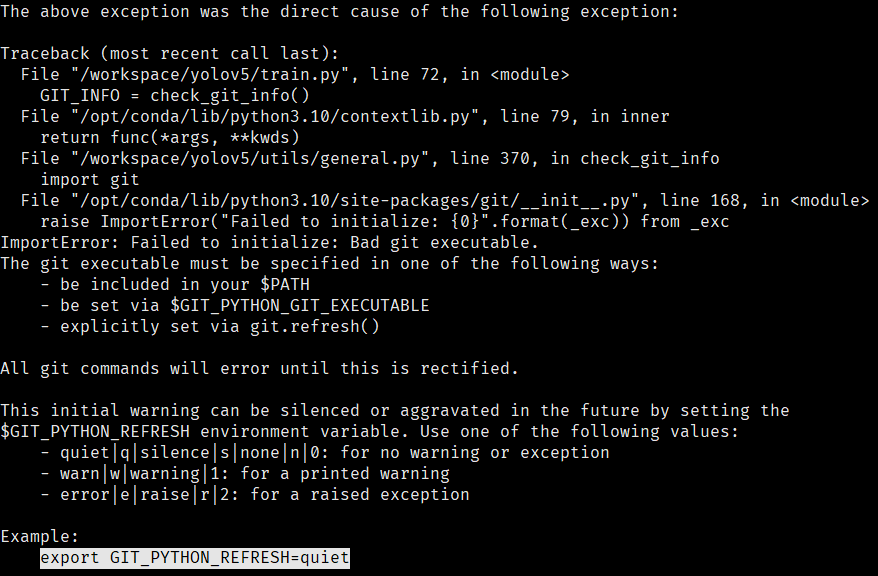
ubuntu下快速搭建docker环境训练yolov5数据集
参考文档 yolov5-github yolov5-github-训练文档 csdn训练博客 一、配置环境 1.1 安装依赖包 前往清华源官方地址 选择适合自己的版本替换自己的源 # 备份源文件 sudo cp /etc/apt/sources.list /etc/apt/sources.list_bak # 修改源文件 # 更新 sudo apt update &&a…...
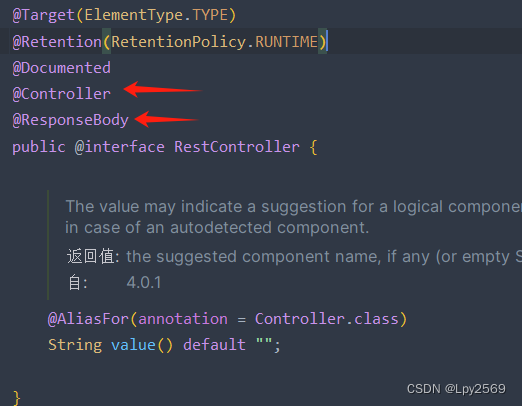
SpringMVC常用注解和用法总结
目标: 1. 熟悉使用SpringMVC中的常用注解 目录 前言 1. Controller 2. RestController 3. RequestMapping 4. RequestParam 5. PathVariable 6. SessionAttributes 7. CookieValue 前言 SpringMVC是一款用于构建基于Java的Web应用程序的框架,它通…...

webpack如何处理css
一、准备工作 新建目录 添加样式 .word {color: red; } index.js添加dom元素,添加一个css word import ./css/index.css;const div document.createElement("div"); div.innerText "hello word!!!"; div.className "word"; do…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
