【人工智能Ⅰ】实验6:回归预测实验
实验6 回归预测实验
一、实验目的
1:了解机器学习中数据集的常用划分方法以及划分比例,并学习数据集划分后训练集、验证集及测试集的作用。
2:了解降维方法和回归模型的应用。
二、实验要求
数据集(LUCAS.SOIL_corr-实验6数据.exl)为 LUCAS 土壤数据集,每一行代表一个样本,每一列代表一个特征,特征包含近红外光谱波段数据(spc列)和土壤理化指标。
1. 对数据集进行降维处理。
2. 统计各土壤理化指标的最大值、最小值、均值、中位数,并绘制各指标的箱型图。
3. 将数据集划分后训练集、验证集及测试集。使用偏最小二乘回归法预测某一指标含量。
4. 打印训练集和验证集的R2和RMSE。
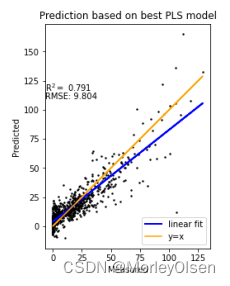
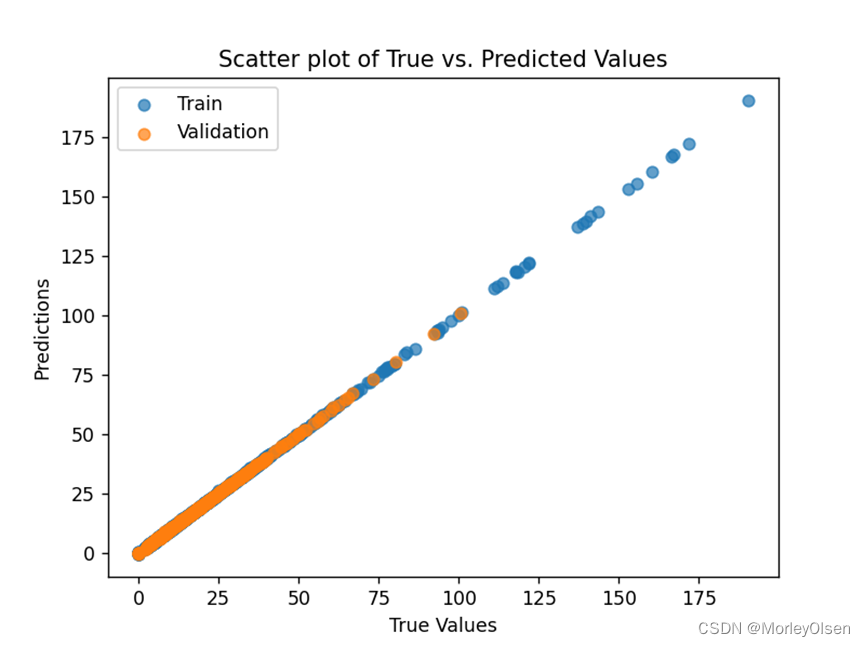
5. 绘制训练集真实标签和模型预测的标签之间的散点图。(如下图所示)
三、实验结果
1:利用PCA进行降维
在任务1中,本实验采用主成分分析(PCA)方法对数据进行降维,整体维度从1201个降低到500个。降维结束后打印数据维度的变化,如下图所示。
![]()
2:统计各个指标的数据并绘制箱型图
在任务2中,本实验采用agg方法对数据进行聚合操作。首先从数据中选择包含了理化指标的列名的列表,然后利用agg方法对目标列进行了多个聚合操作,最终生成了最大值、最小值、均值和中位数的结果,并保存到summary_stats这个二维数据结构之中。最终的处理结果如下图所示。

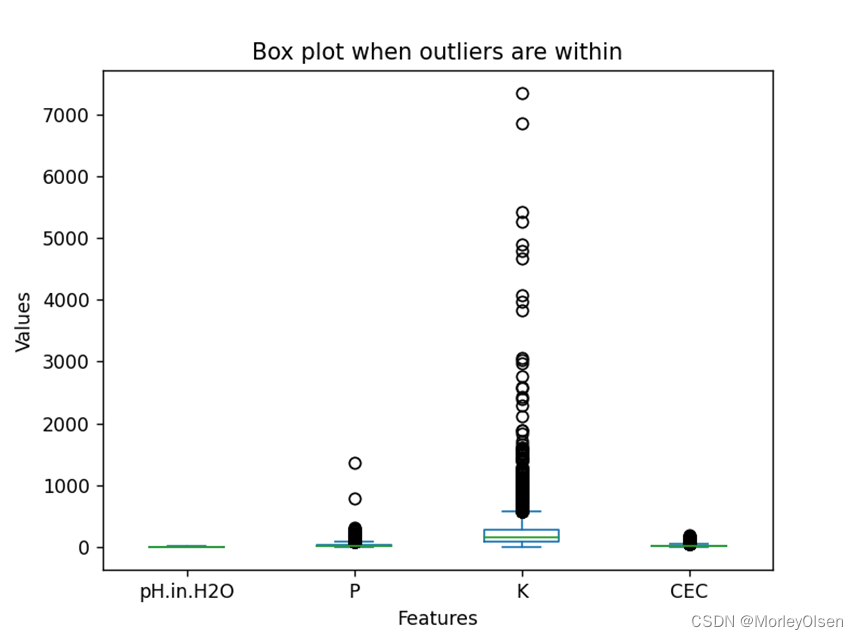
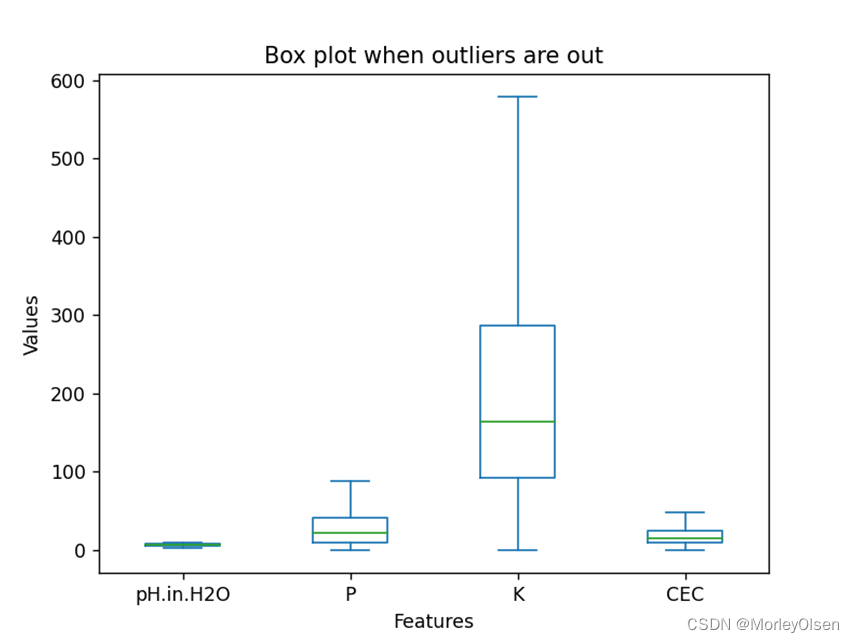
同时,本实验采用plot方法,分别生成了离群点未剔除和剔除后的箱型图。两种情况的最终结果如下图所示,图1为离群点未剔除,图2为离群点剔除。
3:划分数据集,使用偏最小二乘回归法预测pH.in.H2O指标含量
在任务3中,本实验以8:1:1的比例,将数据集随机划分成为训练集、验证集及测试集。
此外,本实验调用机器学习库中的偏最小二乘回归法,通过训练X_train和y_train来预测验证集和测试集的pH.in.H2O指标含量结果。整体代码如下图所示。

4:打印训练集和验证集的R2 和 RMSE
在任务4中,本实验调用机器学习库中的mean_squared_error函数和r2_score函数来计算验证集和测试集上的均方根误差结果和R2结果。整体代码和计算结果如下图所示,图1为调用机器学习依赖的代码,图2为验证集和测试集的均方根误差结果和R2结果。


5:绘制真实标签和模型预测的标签间的散点图。
在任务5中,本实验汇总了模型在训练集、验证集、测试集上的整体表现结果,并进行了绘图展示。最终结果如下图所示,其中蓝色的数据点表示数据来自训练集,橙色的数据点表示数据来自验证集,绿色的数据点表示数据来自测试集,红色的y=x直线为预测结果与真实值相等的标准直线。

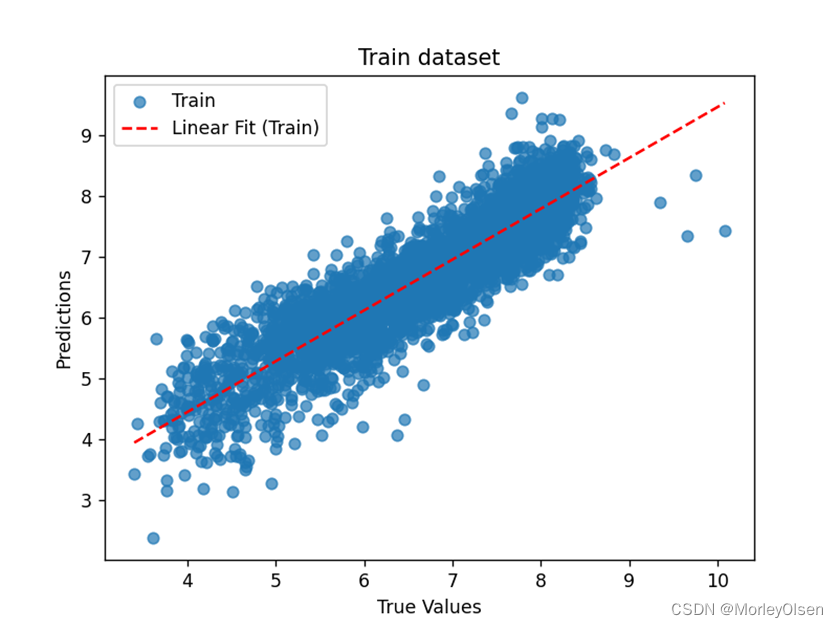
同时,本实验也分别对训练集、验证集、测试集散点图进行了散点图绘制和线性回归模型拟合。最终结果如下图所示,图1为训练集结果,图2为验证集结果,图3为测试集结果,其中红色的直线为使用线性回归模型拟合的回归线。


四、遇到的问题和解决方案
问题1:一开始设置的主成分个数过小(n_components=10),验证集和测试集的R2结果只能达到0.5左右,实验得到的相关性不够好。

解决1:增大主成分个数,并发现当n_components过百后结果较好,此时验证集和测试集的R2结果可以达到0.7+。
问题2:一开始进行特征列选择的时候全选了excel表格的所有列,导致模型直接以因变量进行拟合,验证集和测试集的R2高达0.99。结果如下图所示。

解决2:上述结果显然不符合箱型图的离散点情况。在经过一定分析之后,得知需要在选择需要进行PCA降维的特征列中,排除最后4列理化指标。即把代码更改为【selected_columns = data.columns[:-4].tolist()】。
五、实验总结和心得
1:在计算模型评价机制的时候,mean_squared_error函数中的squared参数用于控制均方误差(MSE)的计算方式。当squared=True时,它表示计算的是均方误差的平方值,即MSE。而当squared=False时,它表示计算的是均方根误差(RMSE),即MSE的平方根。
2:在划分数据集的时候,设置random_state参数可以确保数据集分割的随机性可复现。即多次运行代码时,相同的random_state值会产生相同的随机划分结果。
3:在绘制箱型图的时候,showfliers 参数用于控制箱线图中是否显示离群点(outliers)。如果将 showfliers 设置为 True,则箱线图将显示离群点,如果设置为 False,则离群点将被隐藏,只显示箱体和须部分。
4:linear fit指的是使用线性回归模型对数据进行拟合,即假设目标变量与特征之间存在线性关系。线性回归模型试图找到一条直线(或在多维情况下是一个超平面),以最佳方式拟合数据点,使得观测到的数据点与模型预测的值之间的残差平方和最小化。
5:在本实验中,我们首先对土壤理化指标进行了统计分析,包括计算最大值、最小值、均值和中位数,这有助于了解指标的分布情况和基本统计特性。同时,通过绘制每个指标的箱型图,我们可以直观地感受数据的分布和可能的离群点。
6:在本实验中,如果使用python文件运行,则每次需要较长时间等read_excel完成读入工作。后续思考后发现,可以使用jupyter notebook的ipynb文件运行,这样的话只需要读入一次数据到cell里面,后续就可以不需要重复读入了,实验效率会快很多。
六、程序源代码
各部分的任务操作在多行代码注释下构造。各段代码含有概念注释模块。
| import pandas as pd from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import train_test_split from sklearn.cross_decomposition import PLSRegression from sklearn.metrics import mean_squared_error, r2_score # 读取数据集 data = pd.read_excel(r"C:\Users\86158\Desktop\LUCAS.SOIL_corr-实验6数据.xlsx") """ 任务2:统计各土壤理化指标的最大值、最小值、均值、中位数,并绘制各指标的箱型图。 """ # 获取理化指标的列(数据最后4列) physical_chemical_columns = data.columns[-4:] new_selected = data[physical_chemical_columns] # 统计各理化指标的最大值max、最小值min、均值mean、中位数median summary_stats = data[physical_chemical_columns].agg(['max', 'min', 'mean', 'median']) print("各土壤理化指标的统计信息:") print(summary_stats) # 离群点剔除前的箱型图 boxplot1 = new_selected.plot(kind='box',showfliers=True) plt.title("Box plot when outliers are within") plt.xlabel("Features") plt.ylabel("Values") plt.show() # 离群点剔除后的箱型图 boxplot2 = new_selected.plot(kind='box',showfliers=False) plt.title("Box plot when outliers are out") plt.xlabel("Features") plt.ylabel("Values") plt.show() """ 任务1:对数据集进行降维处理。 """ # 选择需要进行PCA降维的特征列 selected_columns = data.columns[:-4].tolist() # 替换为实际的特征列名称 print("降维前的特征:",selected_columns) # 数据标准化 scaler = StandardScaler() X_scaled = scaler.fit_transform(data[selected_columns]) # 输出降维前的维度 print("降维前数据的维度:", X_scaled.shape) # 使用PCA进行降维 pca = PCA(n_components=500) # 假设降维到10个主成分,根据需要调整 X_reduced = pca.fit_transform(X_scaled) # 输出降维后的维度 print("降维后数据的维度:", X_reduced.shape) """ 任务3:将数据集划分后训练集、验证集及测试集。使用偏最小二乘回归法预测某一指标含量。 """ # 选择要预测的指标列 target_column = -4 # 选择最后一列 X = X_reduced y = data.iloc[:, target_column] # 划分数据集为训练集、验证集和测试集(比例为8:1:1) X_train, X_temp, y_train, y_temp = train_test_split(X, y, test_size=0.2, random_state=42) X_val, X_test, y_val, y_test = train_test_split(X_temp, y_temp, test_size=0.5, random_state=42) # 调用最小二乘法,使用的主成分为10个 pls = PLSRegression(n_components=500) pls.fit(X_train, y_train) # 预测验证集和测试集 y_val_pred = pls.predict(X_val) y_test_pred = pls.predict(X_test) """ 任务4:打印训练集和验证集的R2 和 RMSE。 """ # 评估性能 val_rmse = mean_squared_error(y_val, y_val_pred, squared=False) test_rmse = mean_squared_error(y_test, y_test_pred, squared=False) val_r2 = r2_score(y_val, y_val_pred) test_r2 = r2_score(y_test, y_test_pred) print(f"验证集均方根误差 (RMSE): {val_rmse}") print(f"测试集均方根误差 (RMSE): {test_rmse}") print(f"验证集R^2: {val_r2}") print(f"测试集R^2: {test_r2}") """ 任务5:绘制训练集真实标签和模型预测的标签之间的散点图。 """ y_train_pred = pls.predict(X_train) # 计算训练集、验证集、测试集的线性拟合 train_slope, train_intercept = np.polyfit(y_train, y_train_pred, 1) val_slope, val_intercept = np.polyfit(y_val, y_val_pred, 1) test_slope, test_intercept = np.polyfit(y_test, y_test_pred, 1) # 辅助线的画线范围 min_val = min(min(y_train), min(y_val), min(y_test)) max_val = max(max(y_train), max(y_val), min(y_test)) x_range = [min_val, max_val] # 训练集、验证集、测试集散点图(alpha控制透明度) plt.scatter(y_train, y_train_pred, label='Train', alpha=0.7) # plt.plot(x_range, train_slope * np.array(x_range) + train_intercept, color='blue', linestyle='--', label='Linear Fit (Train)') plt.scatter(y_val, y_val_pred, label='Validation', alpha=0.7) # plt.plot(x_range, val_slope * np.array(x_range) + val_intercept, color='orange', linestyle='--', label='Linear Fit (Validation)') plt.scatter(y_test, y_test_pred, label='Test', alpha=0.7) # plt.plot(x_range, test_slope * np.array(x_range) + test_intercept, color='green', linestyle='--', label='Linear Fit (Test)') # 添加 y=x 的标准预测直线 plt.plot(x_range, x_range, color='red', linestyle='--', label='y=x') # 图注 plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Scatter plot of True vs. Predicted Values") plt.show() # 单独画训练集 plt.scatter(y_train, y_train_pred, label='Train', alpha=0.7) plt.plot(x_range, train_slope * np.array(x_range) + train_intercept, color='red', linestyle='--', label='Linear Fit (Train)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Train dataset") plt.show() # 单独画验证集 plt.scatter(y_val, y_val_pred, label='Validation', alpha=0.7) plt.plot(x_range, val_slope * np.array(x_range) + val_intercept, color='red', linestyle='--', label='Linear Fit (Validation)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Validation dataset") plt.show() # 单独画测试集 plt.scatter(y_test, y_test_pred, label='Test', alpha=0.7) plt.plot(x_range, test_slope * np.array(x_range) + test_intercept, color='red', linestyle='--', label='Linear Fit (Test)') plt.xlabel("True Values") plt.ylabel("Predictions") plt.legend(loc='best') plt.title("Test dataset") plt.show() |
相关文章:

【人工智能Ⅰ】实验6:回归预测实验
实验6 回归预测实验 一、实验目的 1:了解机器学习中数据集的常用划分方法以及划分比例,并学习数据集划分后训练集、验证集及测试集的作用。 2:了解降维方法和回归模型的应用。 二、实验要求 数据集(LUCAS.SOIL_corr-实验6数据…...

前端下载文件的方法-blob下载
前端经常会遇到下载文件的需求,后端一般提供的以下两种方法: 文件地址。后端直接提供要下载的文件地址,常用于图片、音视频等静态文件文件流。后端返回文件流,常用于excel等动态文件 一、a 标签下载 1、直接html使用a标签下载 …...

zookeeper+kafka+ELK+filebeat集群
目录 一、zookeeper概述: 1、zookeeper工作机制: 2、zookeeper主要作用: 3、zookeeper特性: 4、zookeeper的应用场景: 5、领导者和追随者:zookeeper的选举机制 二、zookeeper安装部署: 三…...
-ChatGLM3)
【LangChain实战】开源模型学习(2)-ChatGLM3
介绍 ChatGLM3 是智谱AI和清华大学 KEG 实验室联合发布的新一代对话预训练模型。ChatGLM3-6B 是 ChatGLM3 系列中的开源模型,在保留了前两代模型对话流畅、部署门槛低等众多优秀特性的基础上,ChatGLM3-6B 引入了如下特性: 更强大的基础模型&a…...
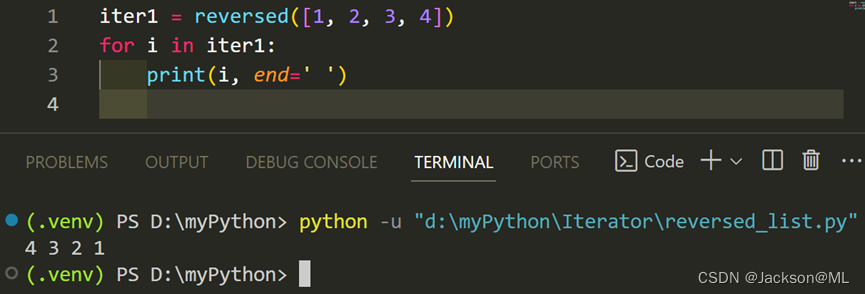
Python编程技巧 – 迭代器(Iterator)
Python编程技巧 – 迭代器(Iterator) By JacksonML Iterator(迭代器)是Python语言的核心概念之一。它常常与装饰器和生成器一道被人们提及,也是所有Python书籍需要涉及的部分。 本文简要介绍迭代器的功能以及实际的案例,希望对广大读者和学生有所帮助。…...

C语言练习题
C语言练习题 文章目录 C语言练习题题目一题目二题目三题目四题目五题目六题目八 题目一 #include <stdio.h> //VS2022,默认对齐数为8字节 union Un {short s[7];int n; };int main() {printf("%zd", sizeof(union Un));return 0; }代码运行结果:> 16 sizeo…...

常见的AI安全风险(数据投毒、后门攻击、对抗样本攻击、模型窃取攻击等)
文章目录 数据投毒(Data Poisoning)后门攻击(Backdoor Attacks)对抗样本攻击(Adversarial Examples)模型窃取攻击(Model Extraction Attacks)参考资料 数据投毒(Data Poi…...

flutter开发实战-为ListView去除Android滑动波纹
flutter开发实战-为ListView去除Android滑动波纹 在之前的flutter聊天界面上,由于使用ScrollBehavior时候,当时忘记试试了,今天再试代码发现不对。这里重新记录一下为ListView去除Android滑动波纹的方式。 一、ScrollBehavior ScrollBehav…...
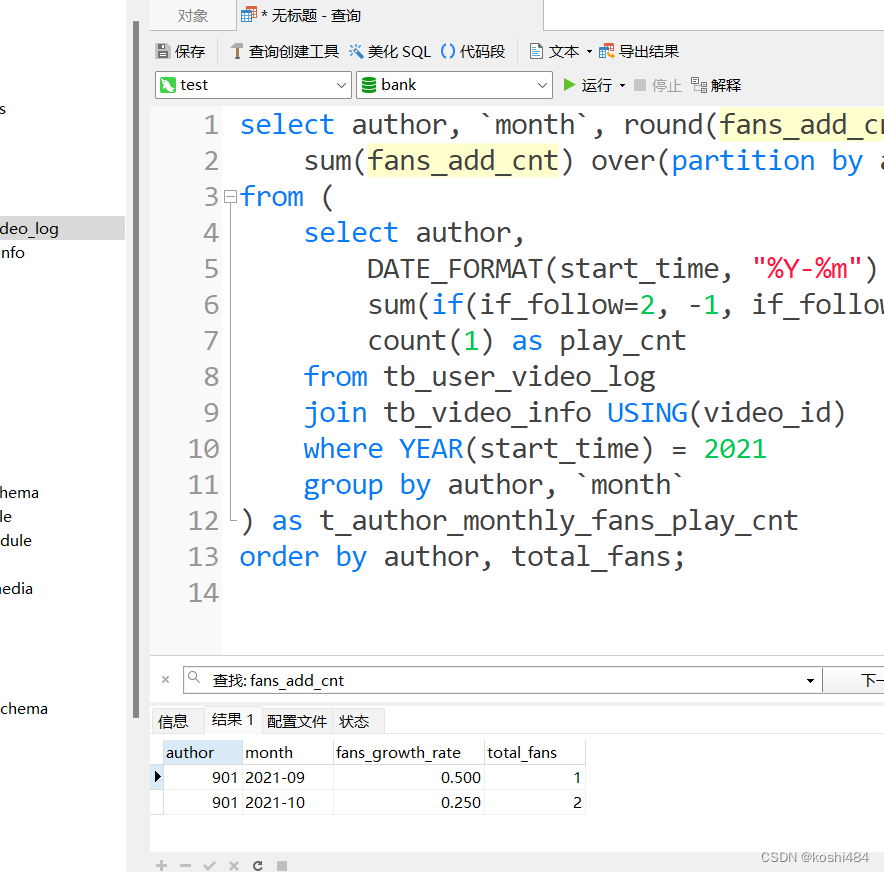
牛客在线编程(SQL大厂面试真题)
1.各个视频的平均完播率_牛客题霸_牛客网 ROP TABLE IF EXISTS tb_user_video_log, tb_video_info; CREATE TABLE tb_user_video_log (id INT PRIMARY KEY AUTO_INCREMENT COMMENT 自增ID,uid INT NOT NULL COMMENT 用户ID,video_id INT NOT NULL COMMENT 视频ID,start_time d…...
ubuntu下快速搭建docker环境训练yolov5数据集
参考文档 yolov5-github yolov5-github-训练文档 csdn训练博客 一、配置环境 1.1 安装依赖包 前往清华源官方地址 选择适合自己的版本替换自己的源 # 备份源文件 sudo cp /etc/apt/sources.list /etc/apt/sources.list_bak # 修改源文件 # 更新 sudo apt update &&a…...
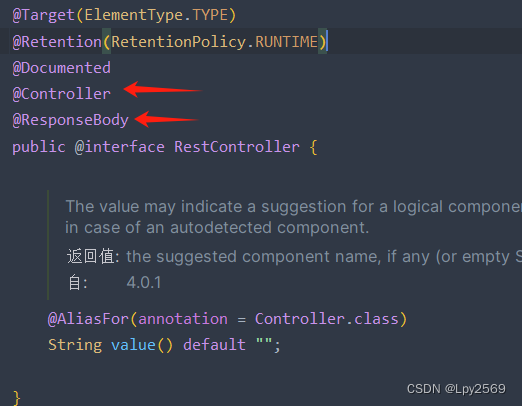
SpringMVC常用注解和用法总结
目标: 1. 熟悉使用SpringMVC中的常用注解 目录 前言 1. Controller 2. RestController 3. RequestMapping 4. RequestParam 5. PathVariable 6. SessionAttributes 7. CookieValue 前言 SpringMVC是一款用于构建基于Java的Web应用程序的框架,它通…...

webpack如何处理css
一、准备工作 新建目录 添加样式 .word {color: red; } index.js添加dom元素,添加一个css word import ./css/index.css;const div document.createElement("div"); div.innerText "hello word!!!"; div.className "word"; do…...

IELTS学习笔记_grammar_新东方
参考: 新东方 田静 语法 目录: 导学简单句… x.1 导学 学语法以应用为主。 基础为:单词,语法 进阶为:听说读写译,只考听说读写。 words -> chunks -> sentences, chunks(语块的重要…...

【计算机组成原理】存储器知识
目录 1、存储器分类 1.1、按存储介质分类 1.2、按存取方式分类 1.3、按信息的可改写性分类 1.4、按信息的可保存性分类 1.5、按功能和存取速度分类 2、存储器技术指标 2.1、存储容量 2.2、存取速度 3、存储系统层次结构 4、主存的基本结构 5、主存中数据的存放 5.…...

vscode配置代码片段
1.ctrl shift p 然后选择 Snippets:Configure User Snippets (配置用户代码片段) 2.选择vue或者vue.json 3.下面为json内容 { “vue-template”: { “prefix”: “modal-table”, “body”: [ “”, " <a-modal v-model:visible“visible” wi…...
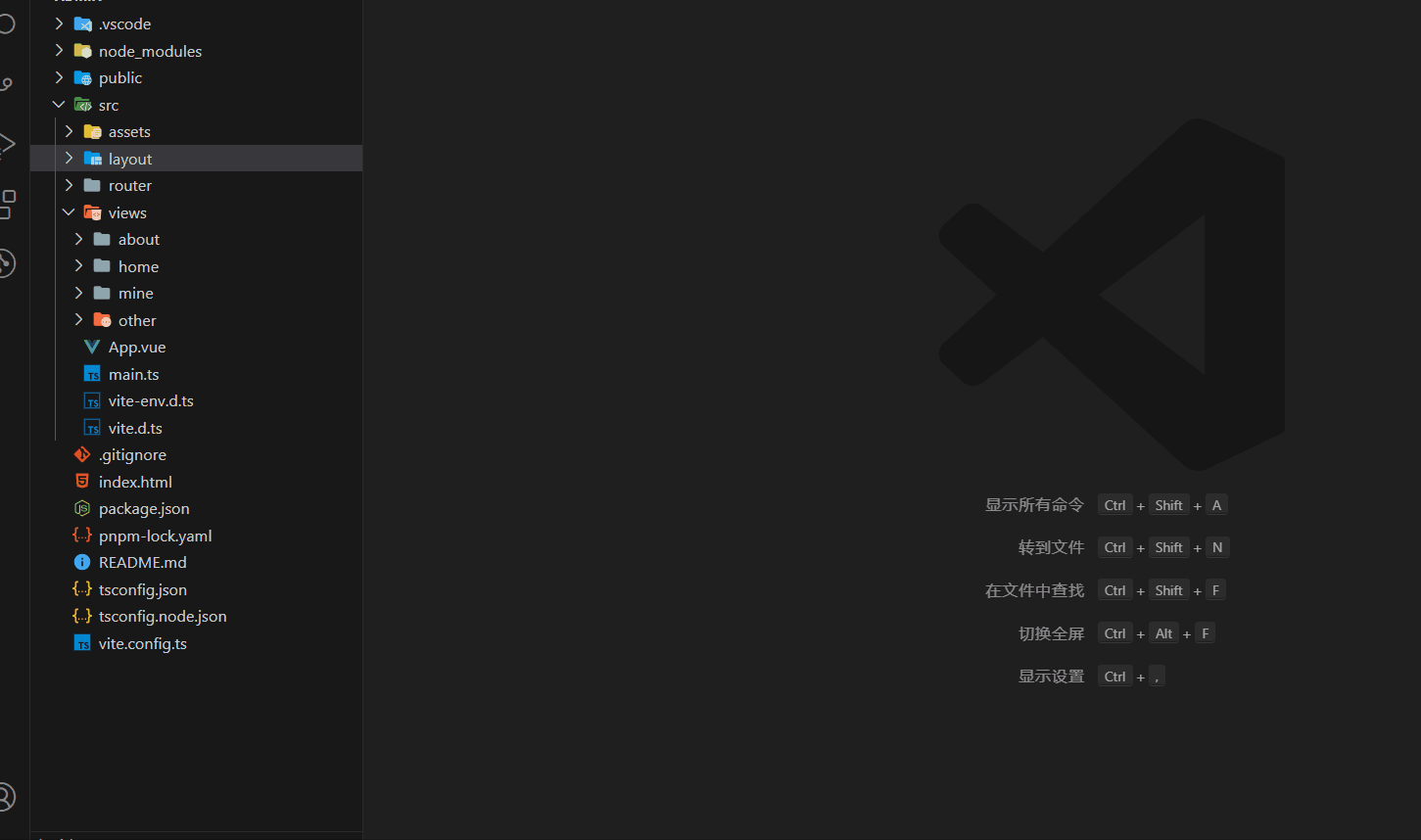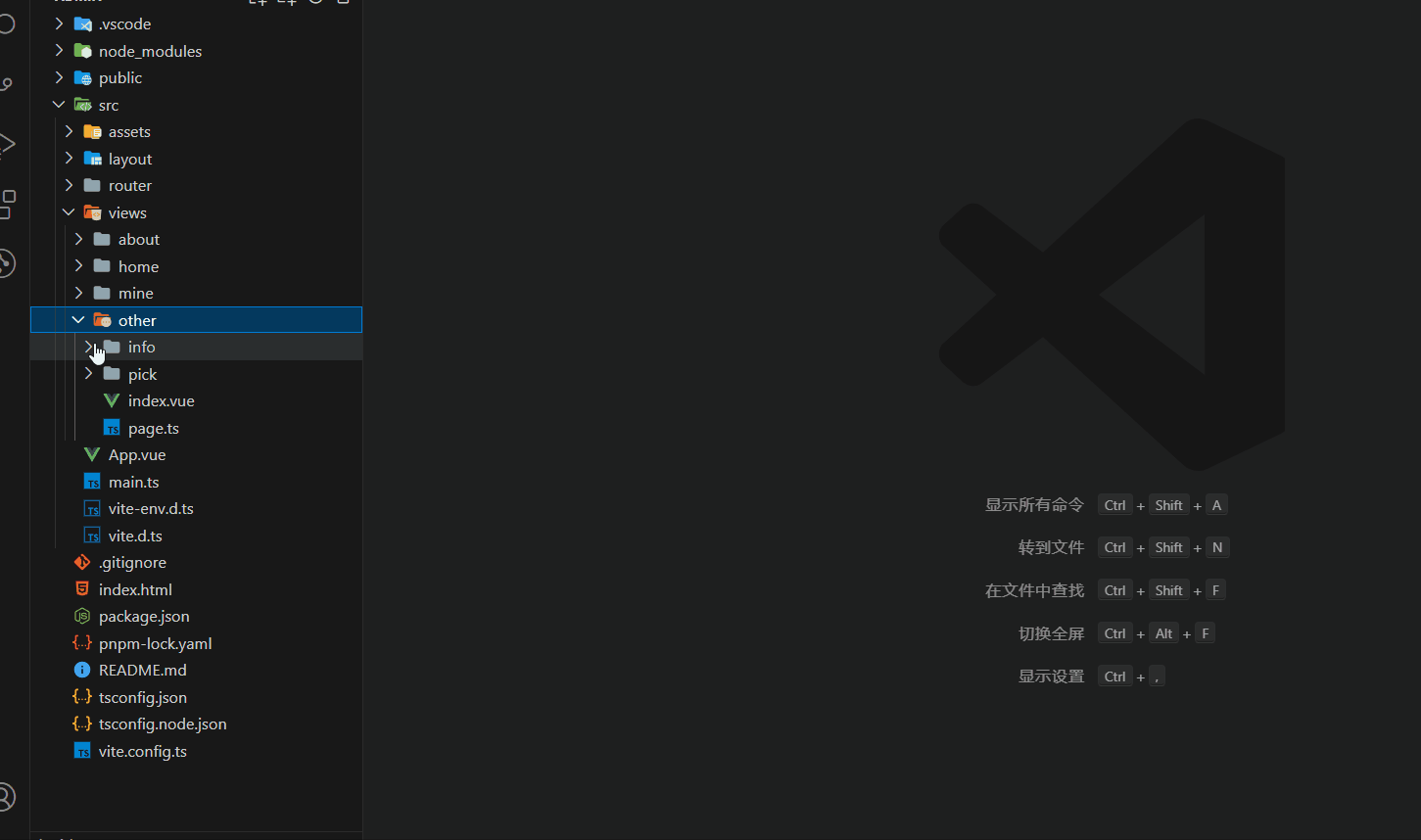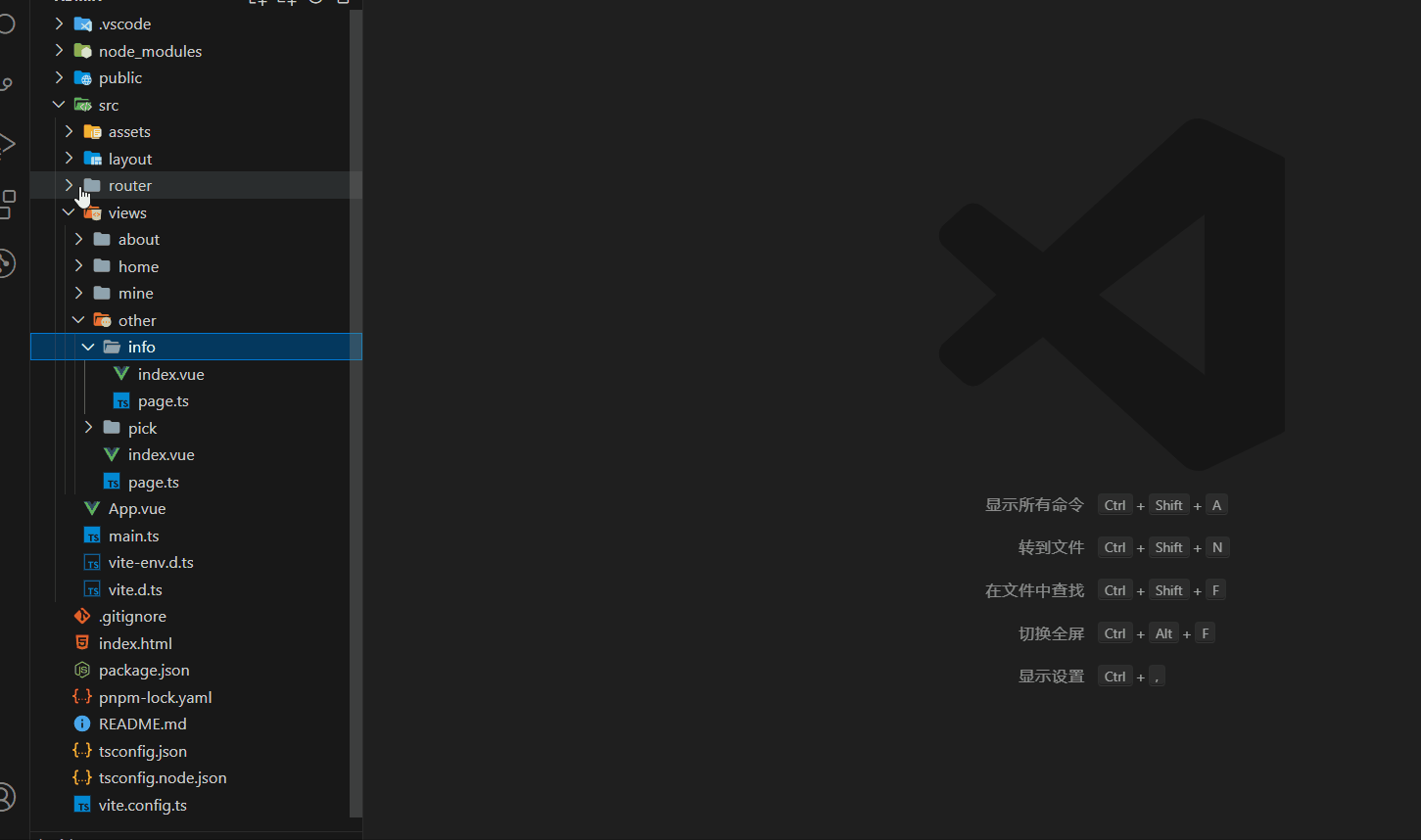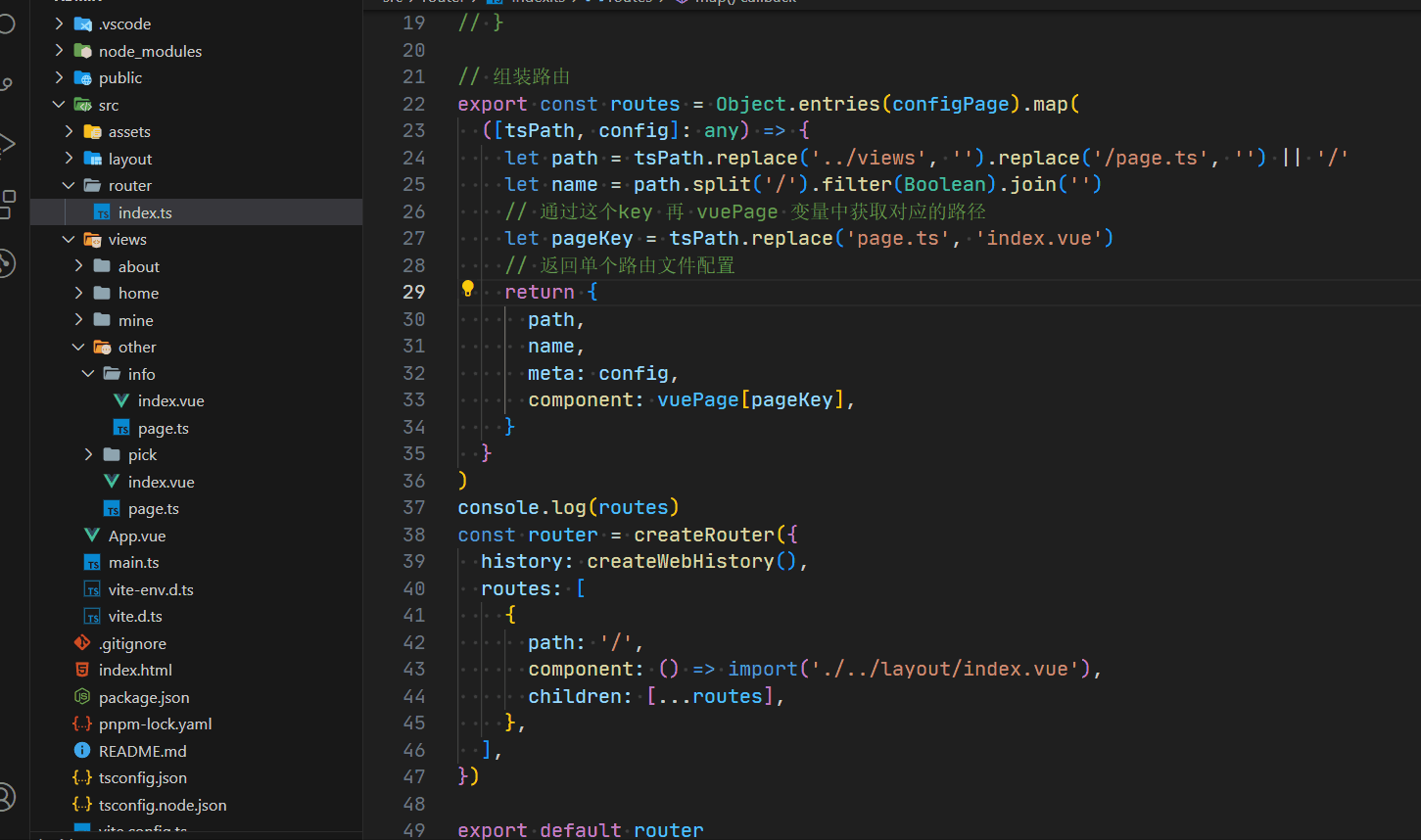
vite脚手架,手写实现配置动态生成路由
参考文档 vite的glob-import vue路由配置基本都是重复的代码,每次都写一遍挺难受,加个页面就带配置下路由 那就利用 vite 的 文件系统处理啊 先看实现效果 1. 考虑怎么约定路由,即一个文件夹下,又有组件,又有页面&am…...

解决浏览器缓存问题
1.index.html文件meta标签添加属性 <meta name"viewport" content"widthdevice-width,initial-scale1.0, maximum-scale1.0, minimum-scale1.0, user-scalableno" viewport-fitcover >2.提前main.html处理逻辑再跳转到index.html页 <script>…...
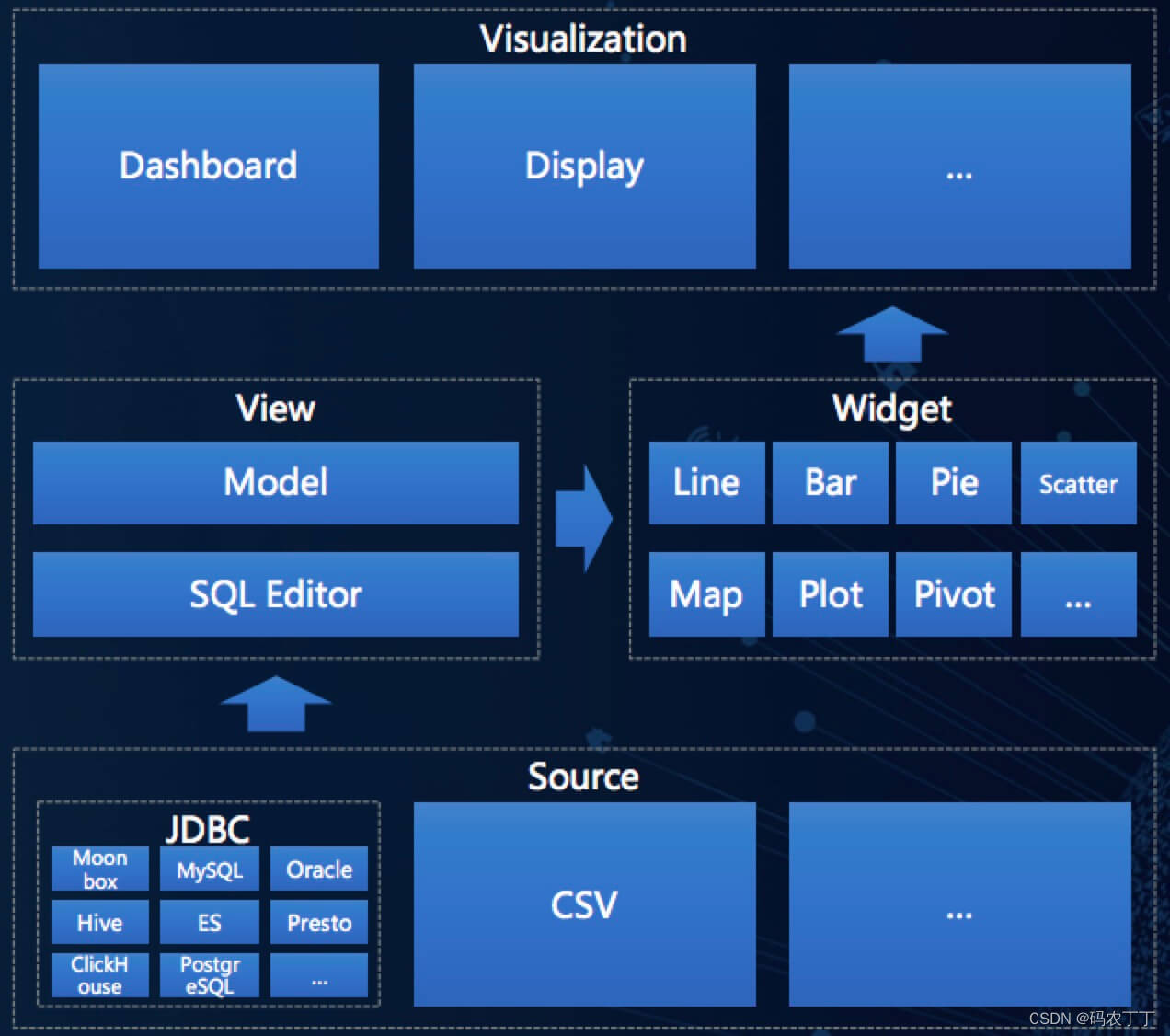
【数据中台】开源项目(2)-Davinci可视应用平台
1 平台介绍 Davinci 是一个 DVaaS(Data Visualization as a Service)平台解决方案,面向业务人员/数据工程师/数据分析师/数据科学家,致力于提供一站式数据可视化解决方案。既可作为公有云/私有云独立部署使用,也可作为…...
Java实现简单飞翔小鸟游戏
一、创建新项目 首先创建一个新的项目,并命名为飞翔的鸟。 其次在飞翔的鸟项目下创建一个名为images的文件夹用来存放游戏相关图片。 用到的图片如下:0~7: bg: column: gameover: ground: st…...

numpy实现神经网络
numpy实现神经网络 首先讲述的是神经网络的参数初始化与训练步骤 随机初始化 任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果我们令所有的初始…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
