《洛谷深入浅出进阶篇》模意义下的乘法逆元+洛谷P3811
什么是乘法逆元?
算数意义上的乘法逆元指的是倒数,即:a*(1/a)=1
所以 1/a 是 a在算数意义下的乘法逆元,或者可以说二者互为逆元。
这有什么用呢?
除以a就等于乘上a的乘法逆元,乘以a等于除以a的乘法逆元。
那么我们回到我们要介绍的新的乘法逆元:模意义上的乘法逆元。(使用条件,当一个正整数做分母的时候)
例如我们要求(x+y)*(x-y)/2 mod p
很显然,对于分子,我们可以直接用模的性质
(x+y)*(x-y)modp = 【(x+y)%p *(x-y)%p】%p
但是,这样的方法只对加减乘有效。
除法的话,由于整除向下取整的原因,我们无法直接使用。这时候就要用到逆元,来代替除法,因为除以一个数取模,等于乘上它在模意义上的逆元,后取模。
ok,那么什么是模意义上的乘法逆元呢?
给出定义: a*x = 1(mod)p,也就是a*x对p取模为1的时候,x就是a 的逆元,所以,当除以a的时候就相当于是乘上a的逆元x。(注意,模只对整数时有意义的,所以我们的变量都应该是整数)
那么我们知道了模意义上的乘法逆元,应该怎么求它的乘法逆元呢?
就可以用到三种方法:扩展欧几里得算法,费马小定理,线性递推。
扩展欧几里得算法:
a*x=1 (mod)p
这个式子可以展开写成:(扩展欧几里得相关文章连接:《洛谷深入浅出进阶篇》 欧几里得算法,裴蜀定理,拓展欧几里得算法————洛谷P1516 青蛙的约会-CSDN博客https://blog.csdn.net/louisdlee/article/details/134751119?spm=1001.2014.3001.5502)
a*x+p*y=1
也就是求x,y的不定方程。
我们由裴蜀定理可知:这个方程只有gcd(a,p)=1的时候才有解,所以,gcd=1是求逆元的前提条件。然后我们直接套exgcd(a,p,x,y)即可
虽然求出来的是a的一个逆元,但是我们由拓展欧几里得可以求出通式,x=x1+k*lcm(a,p)/a (k可以取任意整数)只要不断+模数p就可以求出最小正整数解
2,费马小定理:如果p是质数,且gcd(a,p)=1,a^(p-2)是a的一个乘法逆元。
那么如何求a^(p-2)?
我们可以用到快速幂的方法,s=1,t=p-2 y=a
while(t!=0){
if(p&1==1)s=s*y
y*=y;
t/=2;
}
线性递推求逆元
假如给你1~n个数,让你求所有整数在模p意义下的乘法逆元。你应该怎么办?(n<=1e6)
如果你每次都用exgcd或者费马小定理+快速幂这题是肯定是会超时的,所以我们只能用线性优化了。
只能使用递推的方式来解决这道题
那么我们必须找到递推的式子
假设 inv(i)是i在模意义下的逆元(记住板子即可)
设p=i*q+r,其中q=【p/i】(整除),r=p%i。
第一个式子:p=i*q+r
在模意义下可以得到这样的式子:
i*q+r == 0 (mod p)
变形为: i == -r/q (mod p)
等价于:i== -r * inv(q) (mod p)
两边取倒数:(整数的倒数来表示逆元函数)
1/i == -1/r * q
inv(i) == -inv(r)*q == -inv(r)*【p/i】;
因为 r=p%i,所以r是一定小于当前的i的,怎么求inv(r)
由于我们是递推求逆元,当求到i时,说明i-1,i-2,......1 都求出来了。
所以我们只要注意边界 inv(1) =1即可
但是还是有一个问题,就是,这样求出来的逆元,有些是负数的,如果我们要求逆元的最小正整数应该怎么办?
那也好办,不断在其后面加上p就可以了,当逆元大于0,退出循环。
上代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
using namespace std;
typedef long long LL;
const int N = 3e6 + 7;
LL inv[N];
int main()
{LL n,p;cin >> n>>p;inv[1] = 1;for (int i = 2; i <= n; i++) {LL q = p / i;LL r = p % i;inv[i] = (-q * inv[r]%p)%p;while(inv[i]<0)inv[i]+=p;}for (int i = 1; i <= n; i++)cout << inv[i] << '\n';
}
相关文章:
《洛谷深入浅出进阶篇》模意义下的乘法逆元+洛谷P3811
什么是乘法逆元? 算数意义上的乘法逆元指的是倒数,即:a*(1/a)1 所以 1/a 是 a在算数意义下的乘法逆元,或者可以说二者互为逆元。 这有什么用呢? 除以a就等于乘上a的乘法逆元,乘以…...
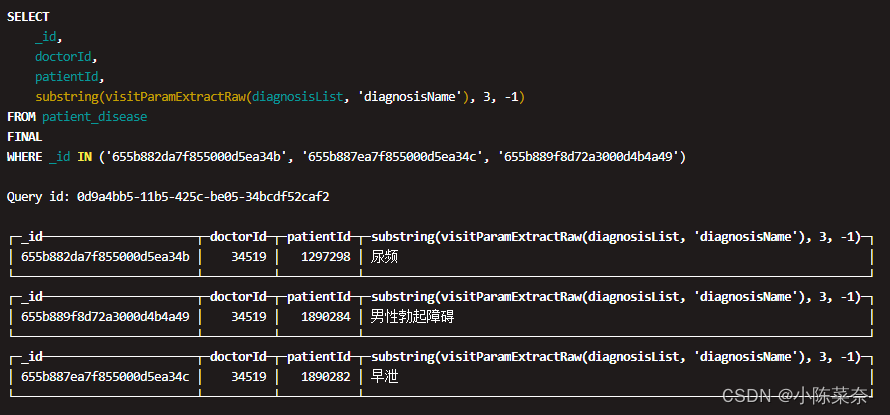
clickhouse -- clickhouse解析复杂JSON数组
举例 - 查数据 select _id,doctorId,patientId,diagnosisList from patient_disease final where diagnosisList is not null limit 3;- 解析数组 SELECT _id,doctorId,patientId,visitParamExtractRaw(diagnosisList,diagnosisName) FROM patient_disease final where _id …...
)
算法leetcode|91. 解码方法(rust重拳出击)
文章目录 91. 解码方法:样例 1:样例 2:样例 3:提示: 分析:题解:rust:go:c:python:java: 91. 解码方法: 一条包含字母 A-Z…...
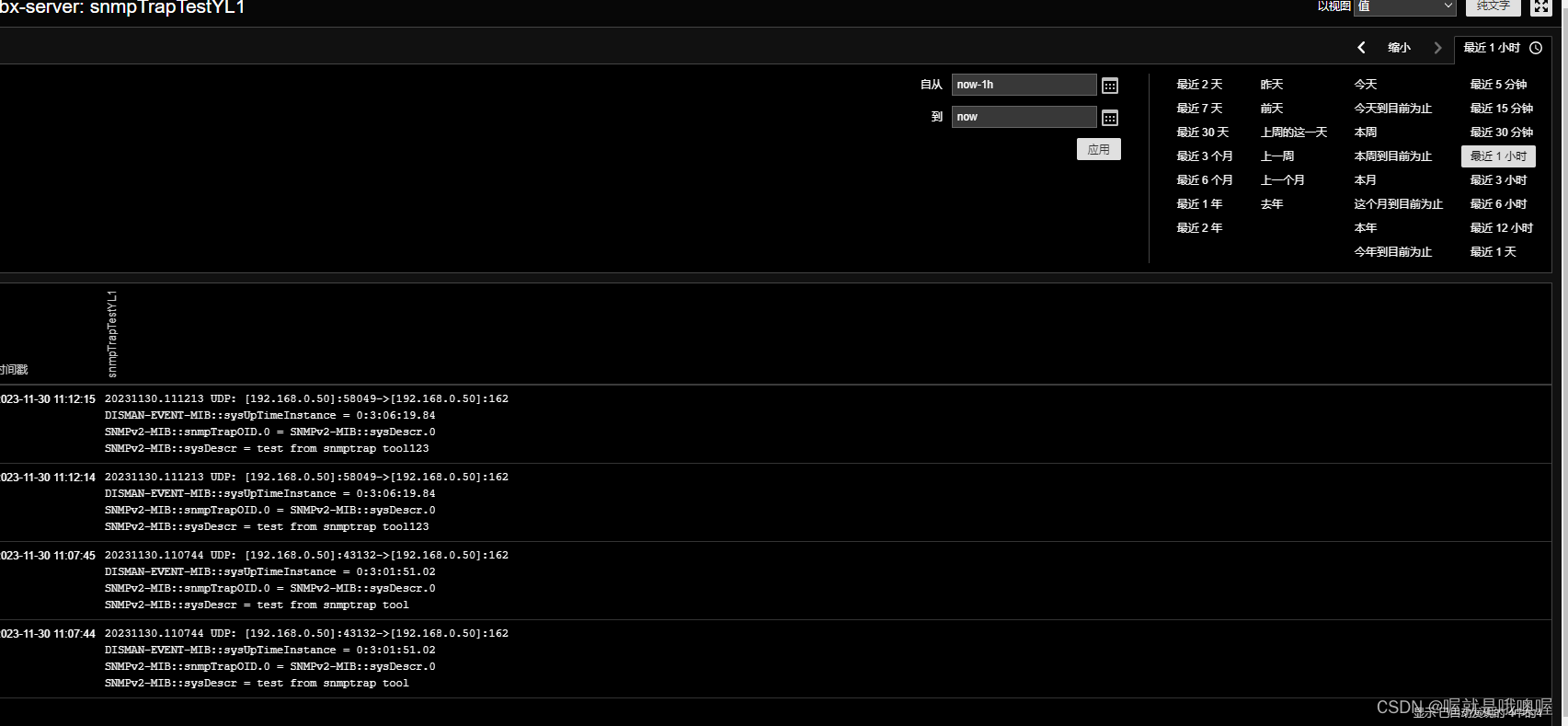
zabbix配置snmp trap--使用snmptrapd和Bash接收器(缺zabbix_trap_handler.sh文中自取)--图文教程
1.前言 我的zabbix的版本是5.0版本,5.0的官方文档没有使用bash接收器的示例,6.0的官方文档有使用bash接收器的示例,但是,下载文件的链接失效?! 这里讲解zabbix-server端配置和zabbix web端配置 2.zabbix-…...
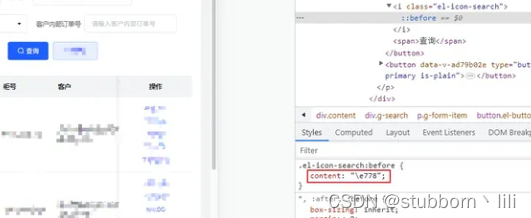
vue: 线上项目element-ui的icon偶尔乱码问题
线上环境偶尔会复现, 具体: 一般使用不会出现这个问题,因为一般引入的是element-ui的css文件,问题出在于为了主题色变化啊,需要用到scss变量引入了scss文件。 import “~element-ui/packages/theme-chalk/src/index”…...
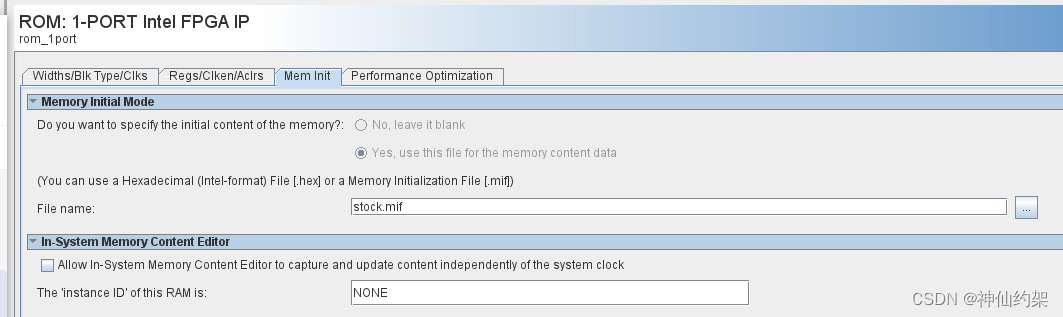
fpga rom 初始化文件的一些心得
目录 可能遇到的问题 问题 解决方案 rom的初始化 用途 文件类型 如何生成初始化文件 示例 Altera Xilinx 可能遇到的问题 问题 altera FPGA的rom找不到初始化文件,编译过程会提示类似的问题 Error(127001): Cant find Memory Initialization File or He…...
)
从零构建属于自己的GPT系列3:模型训练2(训练函数解读、模型训练函数解读、代码逐行解读)
🚩🚩🚩Hugging Face 实战系列 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在PyCharm中进行 本篇文章配套的代码资源已经上传 从零构建属于自己的GPT系列1:文本数据预处理 从零构建属于自己的GPT系列2:语…...
)
Python词频统计(数据整理)
请编写程序,对一段英文文本,统计其中所有不同单词的个数,以及词频最大的前10%的单词。 输入格式: 输入给出一段非空文本,最后以符号#结尾。输入保证存在至少10个不同的单词。 输出格式: 在第一行中输出文本中所有不同单词的个数…...

基本面选股的方法
基本面选股是一种投资策略,主要关注公司的财务状况、盈利能力、行业地位等因素,以判断公司的价值并做出投资决策。以下是基本面选股的具体分析方法和重点: 财务状况分析: 利润表分析:关注公司的净利润、毛利率、营业…...
应用密码学期末复习(3)
目录 第三章 现代密码学应用案例 3.1安全电子邮件方案 3.1.1 PGP产生的背景 3.2 PGP提供了一个安全电子邮件解决方案 3.2.1 PGP加密流程 3.2.2 PGP解密流程 3.2.3 PGP整合了对称加密和公钥加密的方案 3.3 PGP数字签名和Hash函数 3.4 公钥分发与认证——去中心化模型 …...

PAD平板签约投屏-高端活动的选择
传统的现场纸质签约仪式除了缺乏仪式感之外还缺少互动性,如果要将签约的过程投放到大屏幕上更是需要额外的硬件设备成本。相比于传统的纸质签约仪式,平板现场电子签约的形式更加的新颖、更富有科技感、更具有仪式感。 平板签约投屏是应用于会议签字仪式的…...
分布式架构demo
1、外层创建pom 版本管理器 <parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.7.15</version><relativePath/> <!-- lookup parent from repository…...
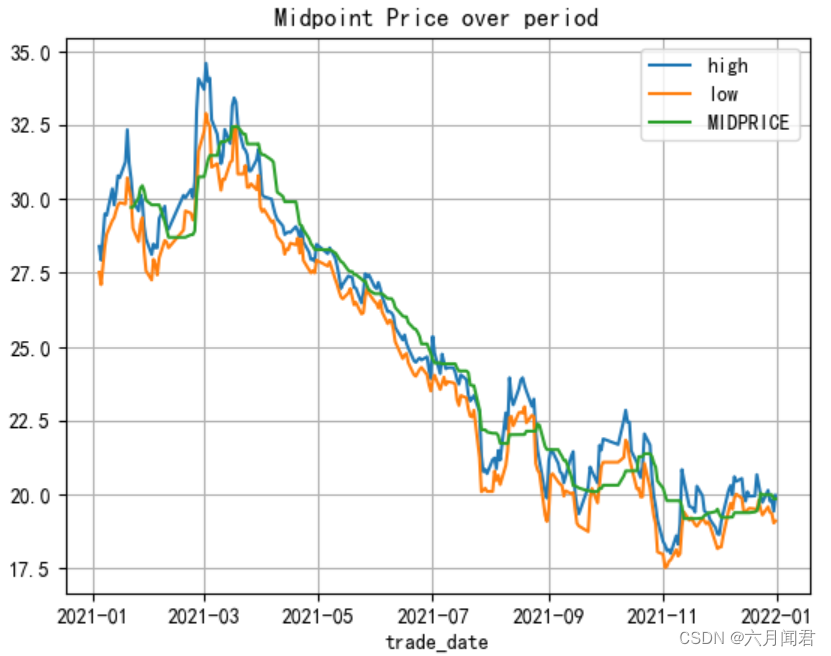
TA-Lib学习研究笔记(二)——Overlap Studies上
TA-Lib学习研究笔记(二)——Overlap Studies 1. Overlap Studies 指标 [BBANDS, DEMA, EMA, HT_TRENDLINE, KAMA, MA, MAMA, MAVP, MIDPOINT, MIDPRICE, SAR, SAREXT, SMA, T3, TEMA, TRIMA, WMA]2.数据准备 get_data函数参数(代码&#x…...

牛客java基础考点1 标识符和变量
牛客java基础考点1 标识符和变量 标识符 字母和数字: 标识符由字母、数字、下划线(_)和美元符号($)组成。其中,标识符必须以字母、下划线或美元符号开头。大小写敏感: Java 是大小写敏感的语言…...
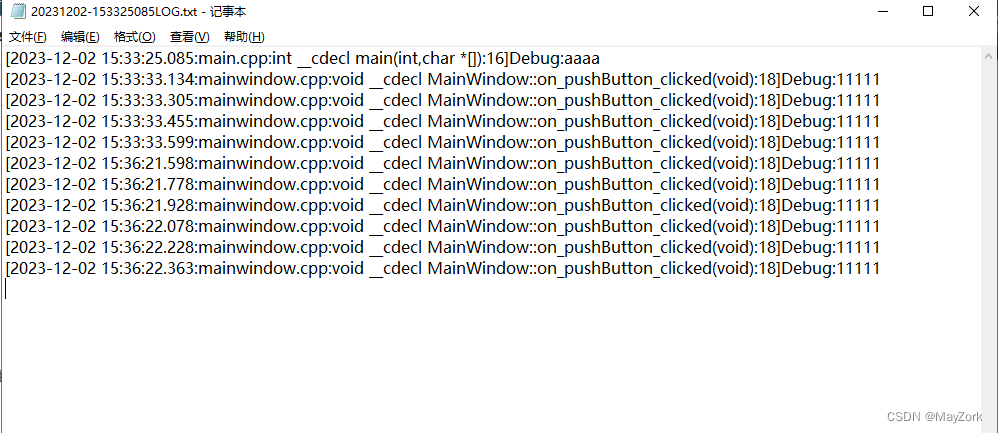
Qt将打印信息输出到文件
将打印信息(qDebug、qInfo、qWarning、qCritial等)输出到指定文件来以实现简单的日志功能。 #include "mainwindow.h" #include <QApplication> #include <QLoggingCategory> #include <QMutex> #include <QDateTime>…...
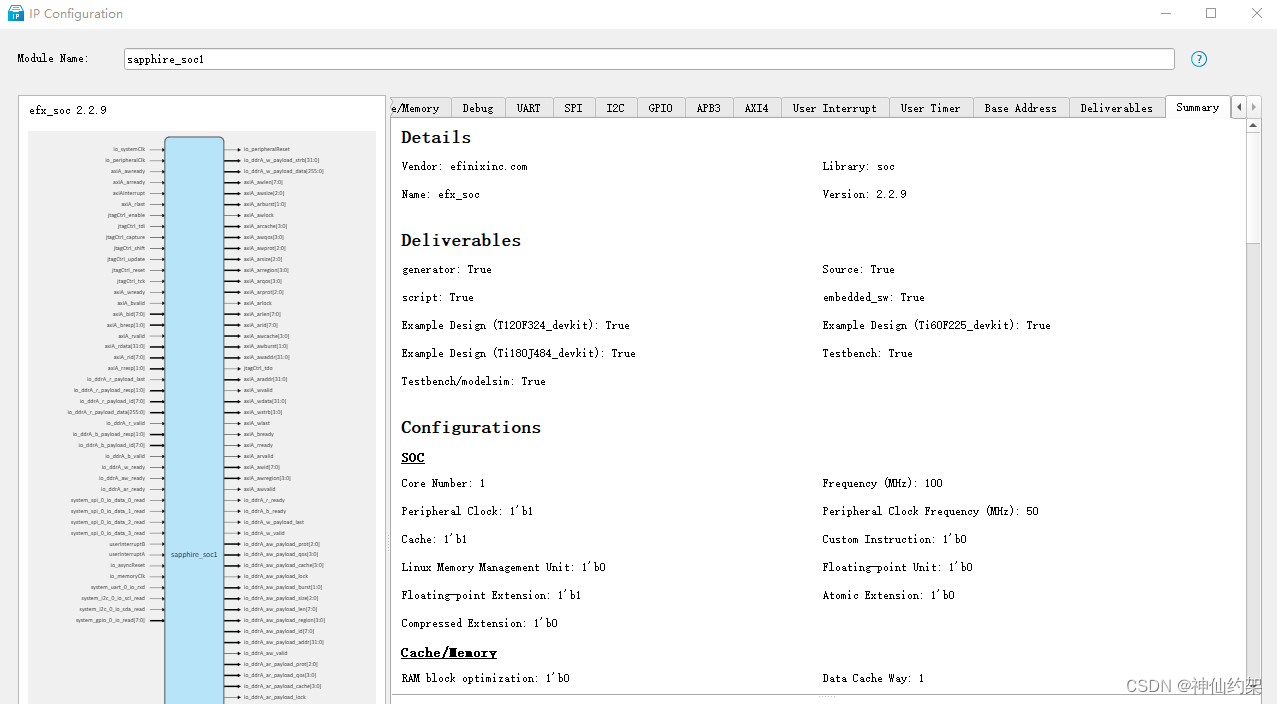
【risc-v】易灵思efinix FPGA sapphire_soc IP配置参数分享
系列文章目录 分享一些fpga内使用riscv软核的经验,共大家参考。后续内容比较多,会做成一个系列。 本系列会覆盖以下FPGA厂商 易灵思 efinix 赛灵思 xilinx 阿尔特拉 Altera 本文内容隶属于【易灵思efinix】系列。 前言 在efinix fpga中使用riscv是一…...

直播的种类及类型
随着网络技术和移动设备的普及,直播已经成为人们娱乐、学习、商业交流等众多领域的重要工具。 直播的种类主要有以下几种: 1.视频直播:这是最常见的直播形式,包括电商直播、婚庆直播、培训直播、家居直播等。 2.图文直播:这种直播形式包括PPT互动直播…...

时间序列数据压缩算法简述
本文简单介绍了时间序列压缩任务的来源,压缩算法的分类,并对常见压缩算法的优缺点进行了简介,爱码士们快来一探究竟呀! 引言 时间序列数据是在许多应用程序和领域中生成的一种基本数据类型,例如金融、医疗保健、交通和…...

智能锁-SI522TORC522方案资料
南京中科微这款SI522目前完全PinTOPin兼容的NXP:RC522、CV520 复旦微:FM17520、FM17522/FM17550 瑞盟:MS520、MS522 国民技术:NZ3801、NZ3802 SI522 是应用于13.56MHz 非接触式通信中高集成度读写卡系列芯片中的一员。是NXP 公司针对&quo…...
 -RTK简单使用)
redux(4) -RTK简单使用
简单使用 1、下载 npm i reduxjs/toolkit react-redux 2、创建 1、在redux/user.js中创建模块user。从reduxjs/toolkit中引入createSlice创建模块片段,我们需要传入name、初始数据initialState、改state的reducers等。最后需要导出reducer和action。 代码如下&a…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
