详解—[C++ 数据结构]—AVL树
目录
一.AVL树的概念
二、AVL树节点的定义
三、AVL树的插入
3.1插入方法
四、AVL树的旋转
1. 新节点插入较高左子树的左侧---左左:右单旋
2. 新节点插入较高右子树的右侧---右右:左单旋
3.新节点插入较高左子树的右侧---左右:先左单旋再右单旋
4.新节点插入较高右子树的左侧---右左:先右单旋再左单旋
5.AVL树的插入代码
五、AVL树的验证
六、AVL树的性能
一.AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)平衡因子 = 右子树高度 - 左子树高度
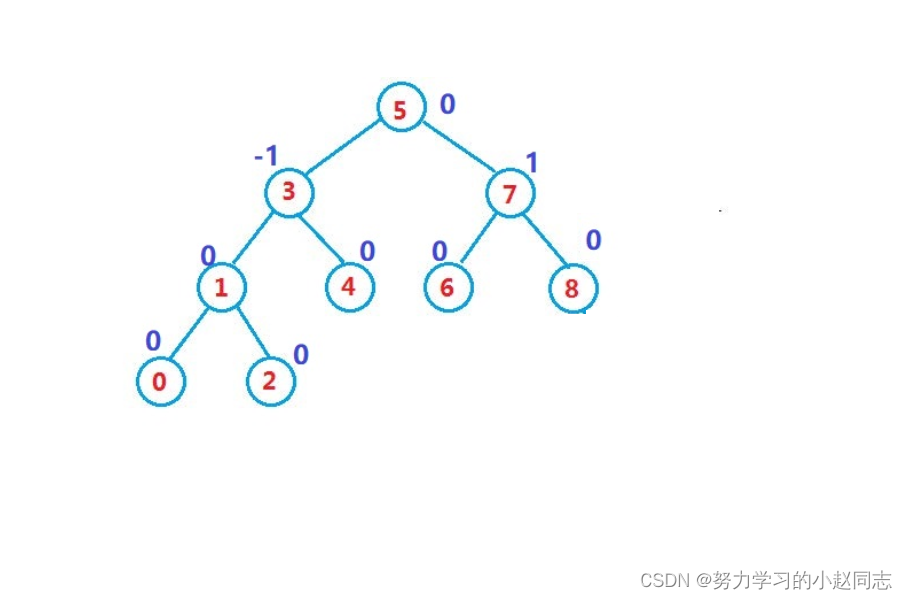
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在 ,搜索时
间复杂度O( )。
二、AVL树节点的定义
AVL树每个节点都会记录他的左右孩子和父节点
并且每个节点记录一下自己的平衡因子
用模板T存储他的数据
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子
};三、AVL树的插入
对于
AVL树的插入,因为它是要结合AVL树的旋转的,所以在本文中,AVL树的插入和AVL树的旋转合起来才是完整的插入过程,所以这里我们主要讲一下插入的大体的一个过程,具体插入的细节及代码实现后面实现
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
3.1插入方法
1. 先按照二叉搜索树的规则将节点插入到AVL树中
2. 新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了
AVL树的平衡性
新节点插入后,他的父节点的平衡因子一定需要调整,在插入之前,父节点
的平衡因子分为三种情况:-1,0, 1,分以下两种情况:
1. 如果新节点插入到父节点的左侧,只需给父节点的平衡因子-1即可
2. 如果新节点插入到父节点的右侧,只需给父节点的平衡因子+1即可
此时:父节点的平衡因子可能有三种情况:0,正负1, 正负2
1. 如果父节点的平衡因子为0,说明插入之前父节点的平衡因子为正负1,插入后被调整成0,此
时满足AVL树的性质,插入成功
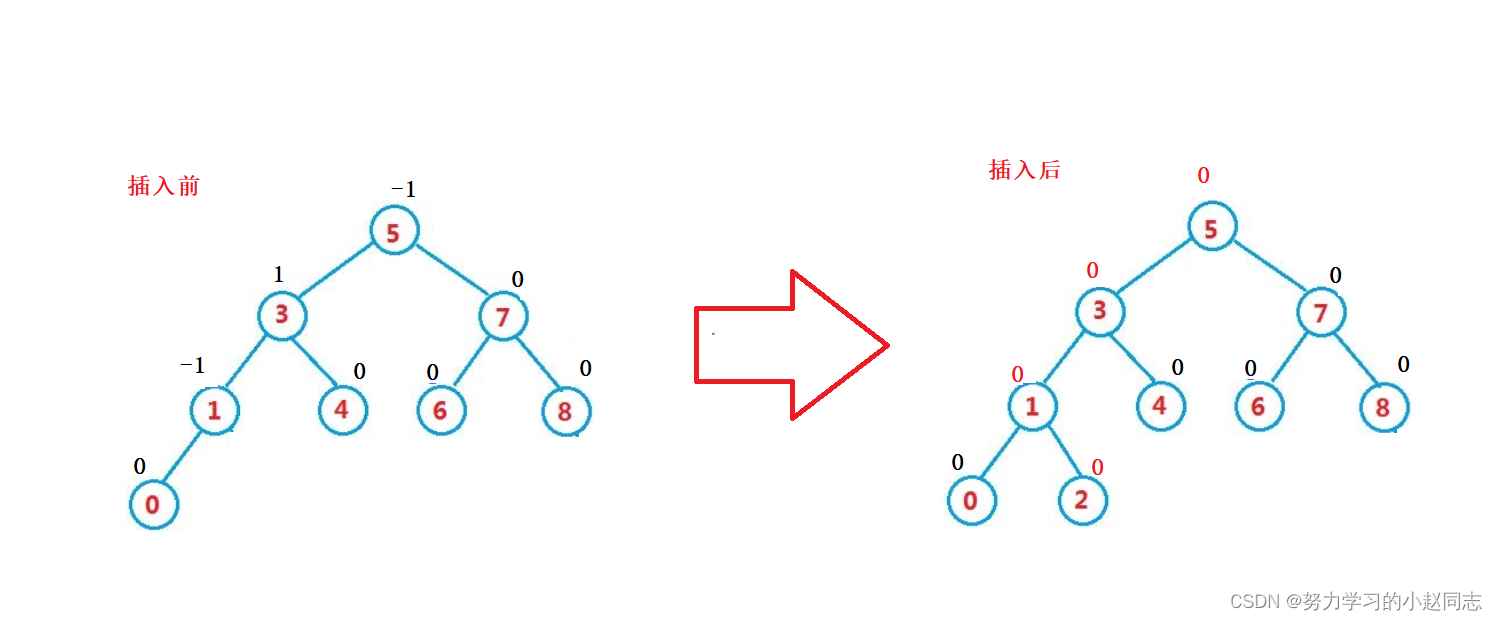
2. 如果父节点的平衡因子为正负1,说明插入前父节点的平衡因子一定为0,插入后被更新成正负1,此时以父节点为根的树的高度增加,需要继续向上更新

3. 如果父节点的平衡因子为正负2,则父节点的平衡因子违反平衡树的性质,需要对其进行旋转
处理

四、AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
1. 新节点插入较高左子树的左侧---左左:右单旋
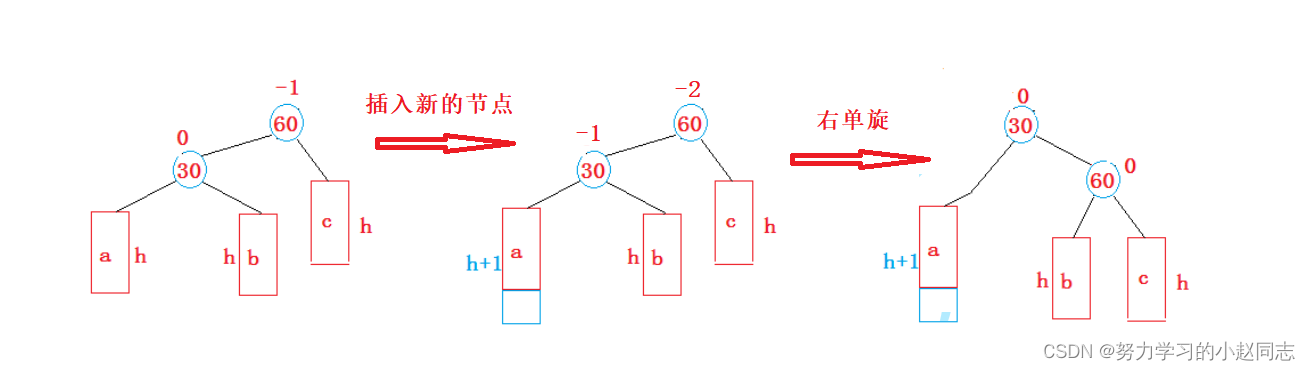

最终,根据我们图上所画的这种右单选的情况,我们可以按照上图写出右旋转的代码:
void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;// 更新节点之间的连接关系parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;Node* pparent = parent->_parent;parent->_parent = subL;if (!pparent){_root = subL;subL->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;}else if (pparent->_right == parent){pparent->_right = subL;}subL->_parent = pparent;}// 更新平衡因子parent->_bf = subL->_bf = 0;}根据上图判断:
我们定义了父亲的左subL和父亲左的右subLR
首先根据上图第一步,把父亲左的右节点给父亲的左,如果subLR不为空,更新一下subLR的父节点
然后把parent链接在subL的右边,(记录一下父亲的父亲(pparent),一会需要subL更新父节点) 更改父亲的父节点为subL
下面就开始更新subL的父节点了
第一步判断旋转前的person是不是根节点,如果是根节点的父亲(pparent)为空,然后把根节点更新为subL,把subL的父节点置为空
如果不是根节点,判断以前pparent的左边还是右边是父亲(parent),让pparent指向父亲改为指向subL,再把subL的父节点更新为pparent
最后,更新平衡因子,把parent和subL的平衡因子置为0
2. 新节点插入较高右子树的右侧---右右:左单旋
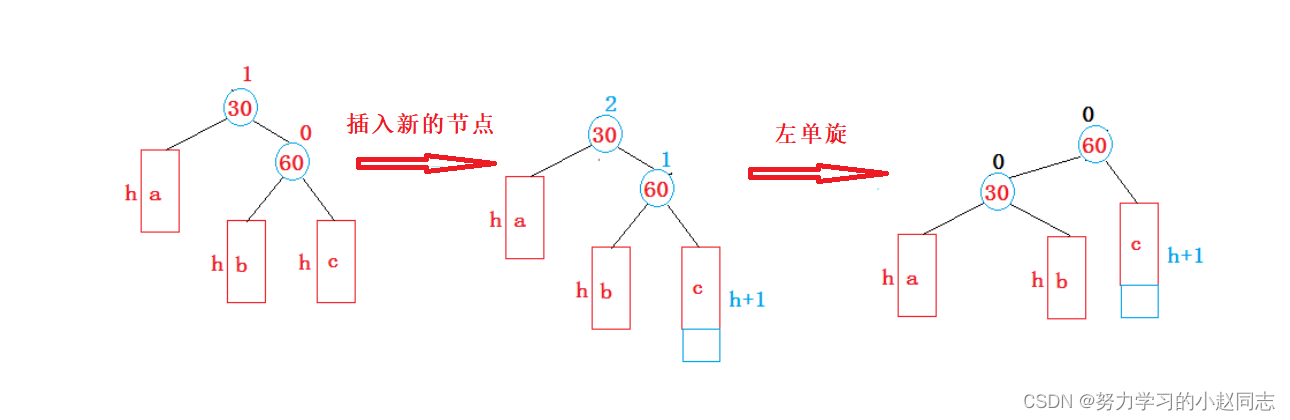
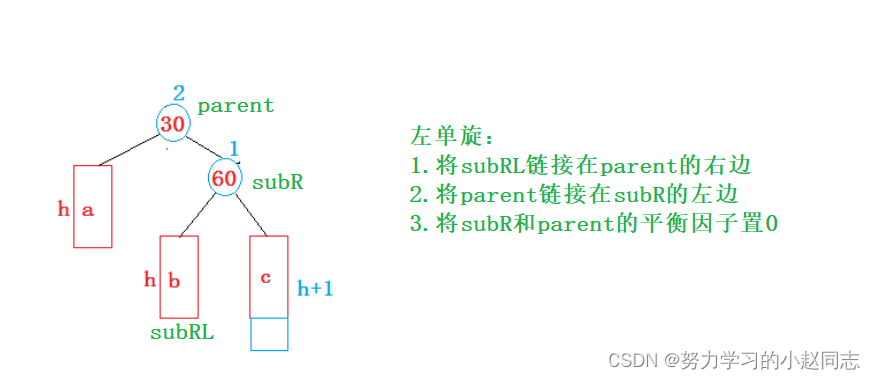
最终,根据我们图上所画的这种右单选的情况,我们可以按照上图写出左旋转的代码:
// 左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;// 更新节点之间的连接关系parent->_right = subRL;if (subRL)// subRL不为空才需要更新它的父亲{subRL->_parent = parent;}subR->_left = parent;Node* pparent = parent->_parent;parent->_parent = subR;if (!pparent)// parent为根时的处理{_root = subR;subR->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}// 更新平衡因子parent->_bf = subR->_bf = 0;}对于左单旋解释,左单旋跟右单旋 两者非常类似,所以这里不再花费篇幅去讲解.
3.新节点插入较高左子树的右侧---左右:先左单旋再右单旋
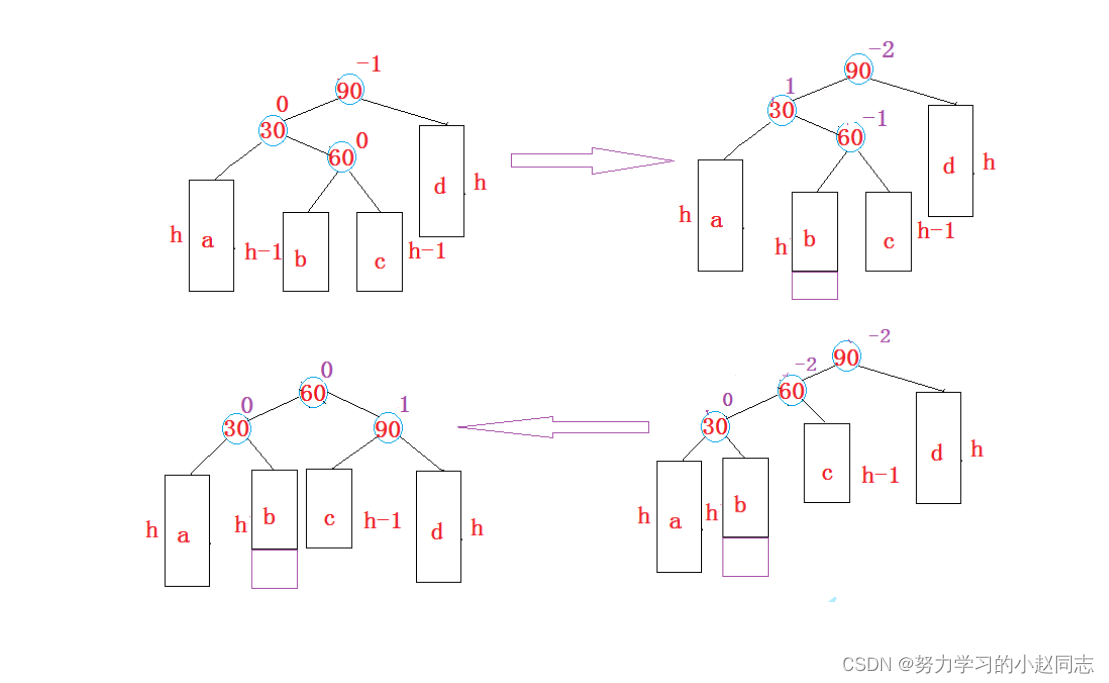
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
// 左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int flag = subLR->_bf;// 记录subLR的平衡因子,最后要依据它来更新其他节点的平衡因子// 依次旋转RotateL(subL);RotateR(parent);// 根据subLR平衡因子的值更新不同插入情况下的平衡因子if (flag == 1)// 说明是在subLR的右子树插入的,那么subLR的左子树变为subL的右子树,subL平衡因子变为-1,subLR和parent的为0{subL->_bf == -1;}else if (flag == -1)// 说明是在subLR的左子树插入的,subLR的右子树最后会被分给parent作为左子树,parent的平衡因子变为-1,subL和subLR的平衡因子变为0{parent->_bf == 1;}}4.新节点插入较高右子树的左侧---右左:先右单旋再左单旋
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int flag = subRL->_bf;// 依次旋转RotateR(subR);RotateL(parent);// 更新平衡因子if (flag == 1){parent->_bf == -1;}else if (flag == -1){subR->_bf == 1;}}5.AVL树的插入代码
bool Insert(const pair<k, v>& kv){// 空树的话,就让插入的那个节点作为根if (!_root){_root = new Node(kv);return true;}// 不是空树,就按照搜索树的性质找到插入的位置和它的父亲Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_kv.first == kv.first){return false;}else if (cur->_kv.first > kv.first){cur = cur->_left;}else{cur = cur->_right;}}// 创建要插入的节点Node* newNode = new Node(kv);// 更新关系,插入节点newNode->_parent = parent;if (parent->_kv.first < newNode->_kv.first){parent->_right = newNode;}else{parent->_left = newNode;}cur = newNode;parent = cur->_parent;while (parent){// 向上更新平衡因子if (cur == parent->_left){--(parent->_bf);}else{++(parent->_bf);}// 检查是否需要调整// 0的话就平衡了// -1或1的话还要向上更新// -2或2的话需要旋转处理if (parent->_bf == 0)// 平衡因子为0,整棵树高度依然不变,只是补了原来低的那边,依然平衡{break;}else if (parent->_bf == 1 || parent->_bf == -1)// 整棵树高度增加了,但是这颗树依然平衡,再往上是否平衡不知道需要继续验证{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 右子树高if (parent->_bf == 2){if (cur->_bf == 1)// 右子树的右子树也高 --> 左单旋{RotateL(parent);}else if (cur->_bf == -1)// 右子树的左子树也高 --> 右左双旋{RotateRL(parent);}}else if (parent->_bf == -2)// 左子树高{if (cur->_bf == -1)// 左子树的左子树也高 --> 右单旋{RotateR(parent);}else if (cur->_bf == 1)// 左子树的右子树也高 --> 左右双旋{RotateLR(parent);}}break;}}return true;}五、AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
1. 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
2. 验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
节点的平衡因子是否计算正确
int Height(Node* root){if (root == nullptr)return 0;int RightHeight = Height(root->_left);int LeftHeight = Height(root->_right);return RightHeight > LeftHeight ? RightHeight + 1 : LeftHeight + 1;}bool _IsBalance(Node* root){if (root == nullptr)return true;//空的话应该返回true,因为不影响平衡int LeftHeight = Height(root->_left);//迭代计算高度int RightHeight = Height(root->_right);if (RightHeight - LeftHeight != root->_bf)//仅仅判断高度是不够的,有可能平衡因子还是错了,所以要对每个平衡因子做检查{cout << "平衡因子现在是:" << root->_bf << endl;cout << "平衡因子应该是:" << (RightHeight - LeftHeight) << endl;return false;//平衡因子错了直接返回}return RightHeight - LeftHeight < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}
六、AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合
相关文章:

详解—[C++ 数据结构]—AVL树
目录 一.AVL树的概念 二、AVL树节点的定义 三、AVL树的插入 3.1插入方法 四、AVL树的旋转 1. 新节点插入较高左子树的左侧---左左:右单旋 2. 新节点插入较高右子树的右侧---右右:左单旋 3.新节点插入较高左子树的右侧---左右:先左单旋…...
卷积神经网络(CNN):乳腺癌识别.ipynb
文章目录 一、前言一、设置GPU二、导入数据1. 导入数据2. 检查数据3. 配置数据集4. 数据可视化 三、构建模型四、编译五、训练模型六、评估模型1. Accuracy与Loss图2. 混淆矩阵3. 各项指标评估 一、前言 我的环境: 语言环境:Python3.6.5编译器…...
有文件实体的后门无文件实体的后门rootkit后门
有文件实体后门和无文件实体后门&RootKit后门 什么是有文件的实体后门: 在传统的webshell当中,后门代码都是可以精确定位到某一个文件上去的,你可以rm删除它,可以鼠标右键操作它,它是有一个文件实体对象存在的。…...

GPT实战系列-大模型训练和预测,如何加速、降低显存
GPT实战系列-大模型训练和预测,如何加速、降低显存 不做特别处理,深度学习默认参数精度为浮点32位精度(FP32)。大模型参数庞大,10-1000B级别,如果不注意优化,既耗费大量的显卡资源,…...

SQL Sever 基础知识 - 数据排序
SQL Sever 基础知识 - 二 、数据排序 二 、对数据进行排序第1节 ORDER BY 子句简介第2节 ORDER BY 子句示例2.1 按一列升序对结果集进行排序2.2 按一列降序对结果集进行排序2.3 按多列对结果集排序2.4 按多列对结果集不同排序2.5 按不在选择列表中的列对结果集进行排序2.6 按表…...

vscode配置使用 cpplint
标题安装clang-format和cpplint sudo apt-get install clang-format sudo pip3 install cpplint标题以下settings.json文件放置xxx/Code/User目录 settings.json {"sync.forceDownload": false,"workbench.sideBar.location": "right","…...
C++ 系列 第四篇 C++ 数据类型上篇—基本类型
系列文章 C 系列 前篇 为什么学习C 及学习计划-CSDN博客 C 系列 第一篇 开发环境搭建(WSL 方向)-CSDN博客 C 系列 第二篇 你真的了解C吗?本篇带你走进C的世界-CSDN博客 C 系列 第三篇 C程序的基本结构-CSDN博客 前言 面向对象编程(OOP)的…...
C++ 指针详解
目录 一、指针概述 指针的定义 指针的大小 指针的解引用 野指针 指针未初始化 指针越界访问 指针运算 二级指针 指针与数组 二、字符指针 三、指针数组 四、数组指针 函数指针 函数指针数组 指向函数指针数组的指针 回调函数 指针与数组 一维数组 字符数组…...

.locked、locked1勒索病毒的最新威胁:如何恢复您的数据?
导言: 网络安全问题变得愈加严峻。.locked、locked1勒索病毒是近期备受关注的一种恶意软件,给用户的数据带来了巨大威胁。本文将深入探讨.locked、locked1勒索病毒的特征,探讨如何有效恢复被其加密的数据,并提供一些建议…...
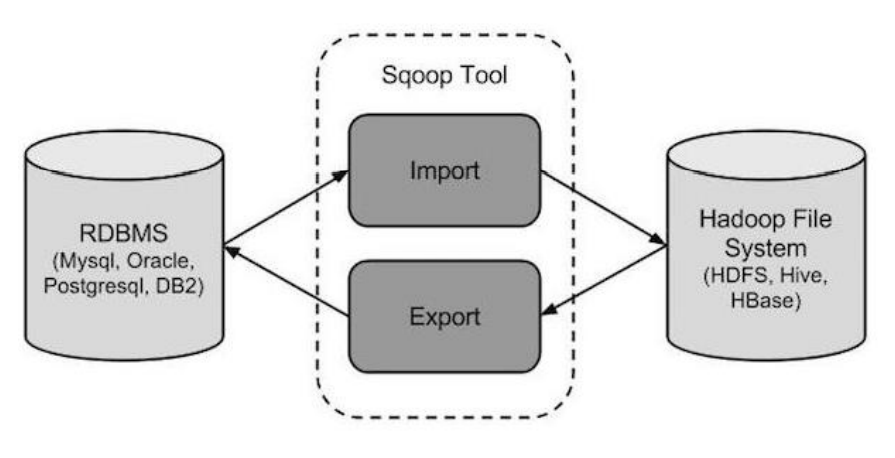
Apache Sqoop使用
1. Sqoop介绍 Apache Sqoop 是在 Hadoop 生态体系和 RDBMS 体系之间传送数据的一种工具。 Sqoop 工作机制是将导入或导出命令翻译成 mapreduce 程序来实现。在翻译出的 mapreduce 中主要是对 inputformat 和 outputformat 进行定制。 Hadoop 生态系统包括:HDFS、Hi…...

【UGUI】实现UGUI背包系统的六个主要交互功能
在这篇教程中,我们将详细介绍如何在Unity中实现一个背包系统的六个主要功能:添加物品、删除物品、查看物品信息、排序物品、搜索物品和使用物品。让我们开始吧! 一、添加物品 首先,我们需要创建一个方法来添加新的物品到背包中。…...
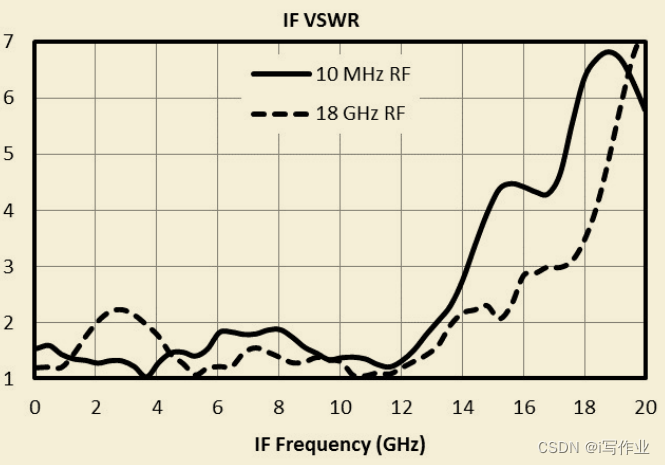
电压驻波比
电压驻波比 关于IF端口的电压驻波比 一个信号变频后,从中频端口输出,它的输出跟输入是互异的。这个电压柱波比反映了它输出的能量有多少可以真正的输送到后端连接的器件或者设备。...

Open3D 最小二乘拟合二维直线(直接求解法)
目录 一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。爬虫网站自重。 一、算法原理 平面直线的表达式为: y = k x + b...
)
面试题目总结(二)
1. IoC 和 AOP 的区别 控制反转(Ioc) 和面向切面编程(AOP) 是两个不同的概念,它们在软件设计中有着不同的应用和目的。 IoC 是一种基于对象组合的编程模式,通过将对象的创建、依赖关系和生命周期等管理权交给外部容器或框架来实现程序间的解耦。IoC 的…...

TrustZone概述
目录 一、概述 1.1 在开始之前 二、什么是TrustZone? 2.1 Armv8-M的TrustZone 2.2 Armv9-A Realm Management Ext...

[go 面试] Go Kit中读取原始HTTP请求体的方法
关注公众号【爱发白日梦的后端】分享技术干货、读书笔记、开源项目、实战经验、高效开发工具等,您的关注将是我的更新动力! 在Go Kit中,如果你想读取未序列化的HTTP请求体,可以使用标准的net/http包来实现。以下是一个示例,演示了如何完成这个任务: package mainimport …...

小程序如何刷新当前页面?
在小程序中,刷新当前页面通常有两种方法: 使用 wx.navigateBack 方法: wx.navigateBack({delta: 1 }) 这将返回上一页,并刷新页面。你可以通过调整 delta 参数来控制返回的页面数。例如,如果你想要返回到两页之前的页…...

ChatGPT使用路径:从新手到专家的指南
原文&精华文章&转载注明:ChatGPT与日本首相交流核废水事件-精准Prompt... hello,我是小索奇,有任何问题或者需要帮助的都可以在这里找到我或者留言哈 一、初识ChatGPT 什么是ChatGPT? ChatGPT是一种大型语言模型&…...
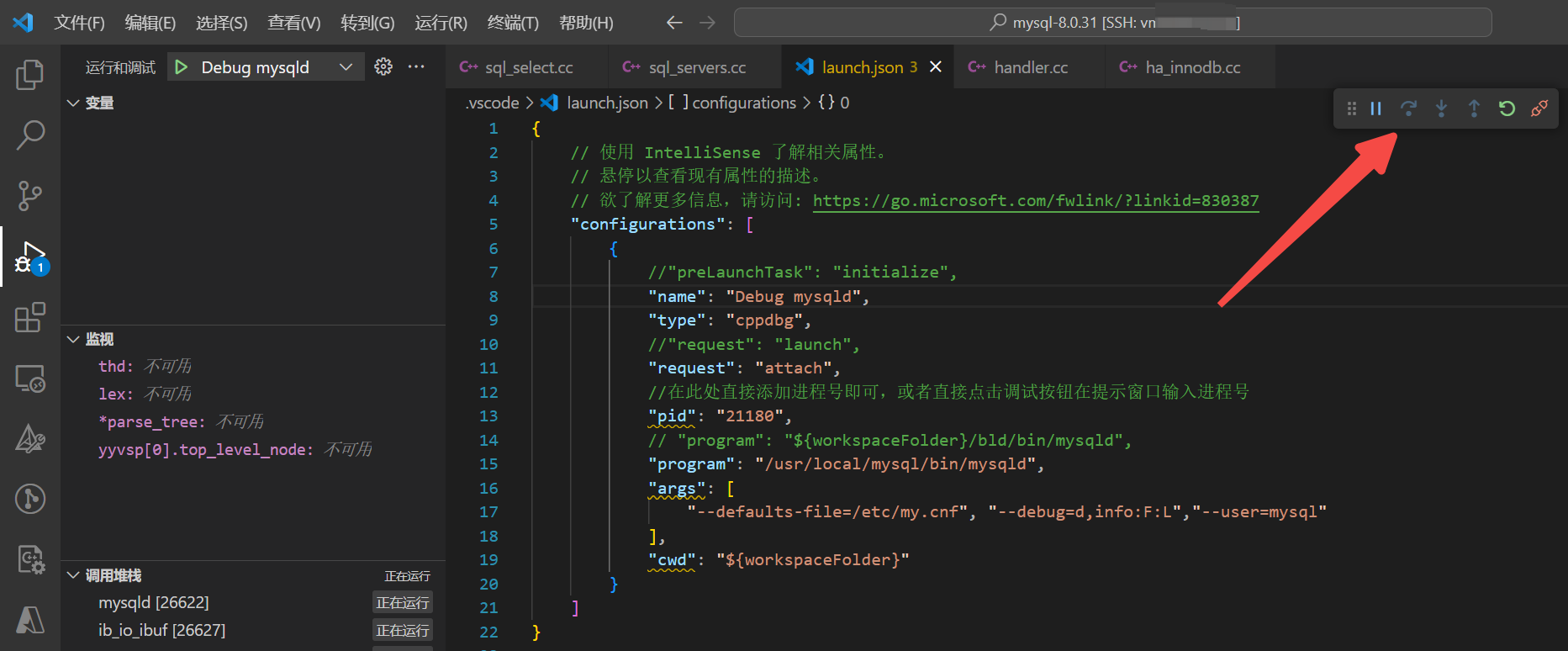
VsCode 调试 MySQL 源码
1. 启动 MySQL 2. 查看 MySQL 进程号 [root ~]# ps -ef | grep mysqld root 21479 1 0 Nov01 ? 00:00:00 /bin/sh /usr/local/mysql/bin/mysqld_safe --datadir/usr/local/mysql/data --pid-file/usr/local/mysql/data/mysqld.pid root 26622 21479 0 …...

Mysql中的正经行锁、间隙锁和临键锁
行锁、间隙锁和临键锁是数据库中的三种不同类型的锁,三者都属于行锁,第一个一般叫他正经的行锁(《Mysql是怎样运行的》一书中的说法)。 行锁(Row Lock):行锁是指对数据表中的某一行进行的锁定操…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
