【C语言】深入理解C语言中的数学运算和类型转换
文章目录
- 引言
- 取负运算的奥秘
- 源码探索
- 分析与解读
- 浮点数运算的精细差异
- 源码分析
- 精度损失与隐式类型转换
- 精度和除零运算探究
- float类型和double类型的精度各是多少(即十进制有效位的位数)?
- 在你的机器上,“负数开方”是如何处理的(如“-8.0/0”、“sqrt(-4.0)”的运算结果)?
- 在你的机器上,整数除0和浮点数除0的运行结果各是什么?为什么会有不同的运行结果?,并将“-6.0/0”和“-6/0”的运行结果进行比较。
- 结语
引言
在编程中,理解各种数据类型的运算规则是至关重要的。本文将通过几个示例,深入探讨C语言中整数和浮点数的取负运算、浮点数的精度问题以及除零运算的处理机制。
取负运算的奥秘
源码探索
分析以下简单的C程序:
int main()
{int x = -2147483648;int y = 3;float f = 1.5;printf("%d\n", -x > y);printf("%f\n", -f);return 0;
}
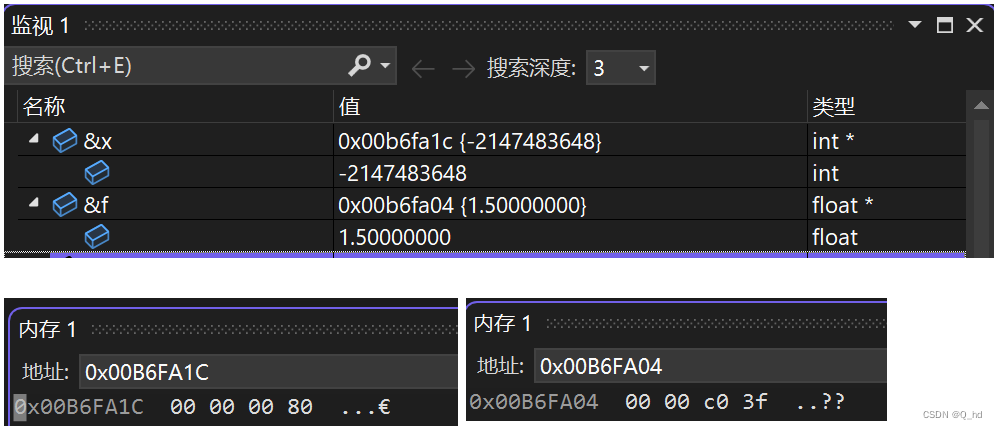
分析与解读
-
当我们对整数
x取负时,由于它已经是32位整数的最小可能值,其补码表示无法再表示一个更大的正数,因此-x仍然等于-2147483648。这导致-x > y的判断为假,因此第一个printf输出为0。 -
另一方面,浮点数
f的取负运算简单明了,结果自然就是-1.5。因此,第二个printf输出-1.500000。
浮点数运算的精细差异
源码分析
接下来,我们看一个涉及浮点数运算的程序:
#include <stdio.h>
int main()
{float x = -1.5e38;float y = 1.5e38;float z = 1.0;int i = (x + y) + z;int j = x + (y + z);printf("%d\n", i == j);return 0;
}

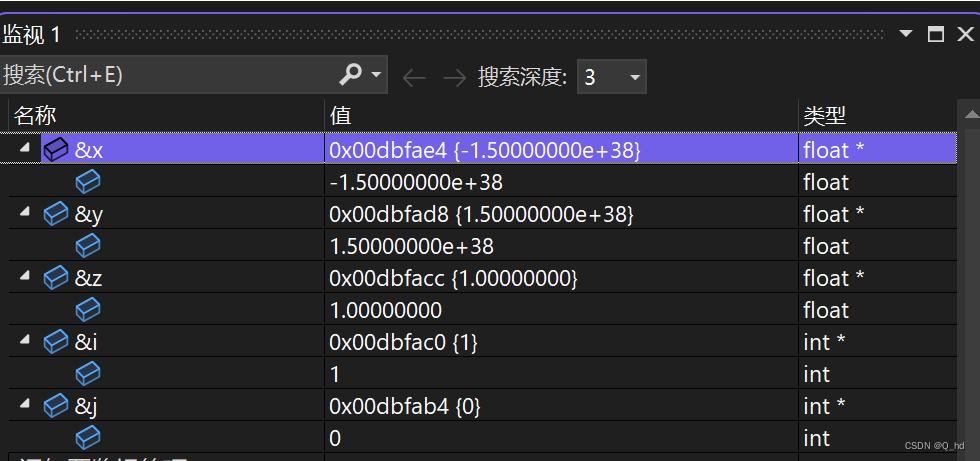
精度损失与隐式类型转换
-
在上述代码中,我们试图通过不同的运算顺序来比较结果是否相同。然而,由于浮点数的精度限制和整数类型的截断行为,
i和j得到的结果很可能不同,因此输出为0(false)。这个例子清晰地展示了浮点数运算中的精度损失和隐式类型转换可能导致的意外结果。 -
在表达式
(x + y) + z中,x和y是浮点数,而 z 是浮点数转换为整数后的结果。根据C语言的运算规则,当一个浮点数和一个整数进行运算时,整数会被自动转换为浮点数。因此,(x + y)的结果是一个浮点数,再加上z后得到的结果也是一个浮点数。然而,由于i是整型变量,这个浮点数会被截断成整数并赋值给i。
类似地,在表达式x + (y + z)中,y和z是浮点数,而x是一个负浮点数。同样根据C语言的运算规则,负浮点数和浮点数进行运算时,会进行隐式类型转换,使结果仍为浮点数。因此,(y + z)的结果是一个浮点数,再加上x后得到的结果也是一个浮点数。然而,由于j是整型变量,这个浮点数会被截断成整数并赋值给j。 -
如果想要避免隐式类型转换,可以显式地进行类型转换操作,将浮点数转换为整型。例如,可以使用
int(i)或int(j)来将浮点数转换为整型。这样可以确保进行精确的整数比较
精度和除零运算探究
float类型和double类型的精度各是多少(即十进制有效位的位数)?
#include <stdio.h>
#include <float.h>int main() {printf("float类型的十进制有效位数: %d\n", FLT_DIG);printf("double类型的十进制有效位数: %d\n", DBL_DIG);return 0;
}
在C语言中,可以使用float.h头文件中定义的常量来获取float和double类型的精度信息。具体而言,FLT_DIG和DBL_DIG分别表示float和double类型的十进制有效位数。
这段代码将打印出float和double类型的十进制有效位数。在大多数系统上,你会看到类似以下的输出:
float类型的十进制有效位数: 6
double类型的十进制有效位数: 15
这样就直接获取了float和double类型的十进制有效位数,而无需手动计算。
在你的机器上,“负数开方”是如何处理的(如“-8.0/0”、“sqrt(-4.0)”的运算结果)?
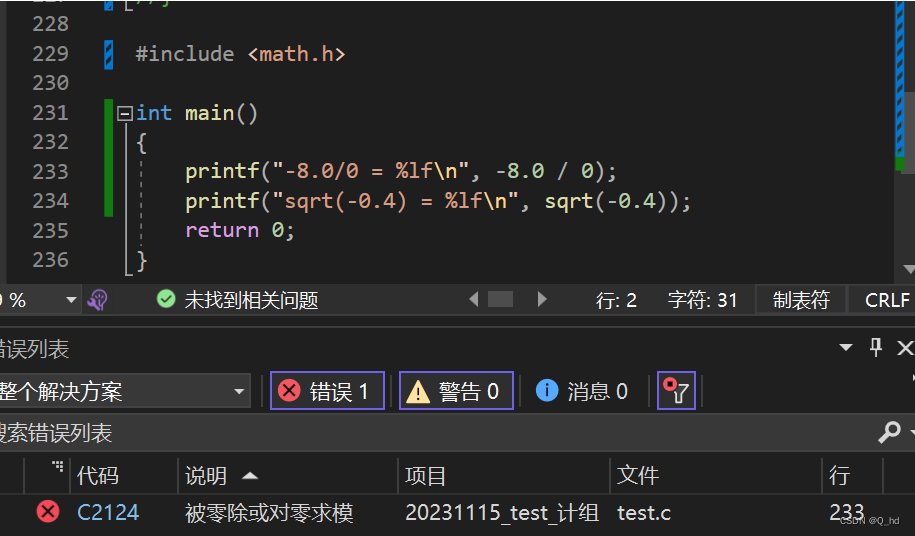
- 当进行表达式
-8.0/0进行计算时,结果会被认为是负无穷大(-∞)。这是因为除以零是一个非法的操作,C语言规定将其视为一种特殊情况,结果被定义为负无穷大或正无穷大。
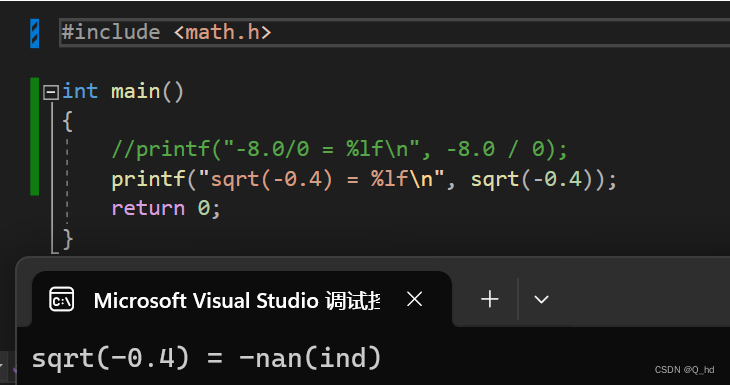
- 当进行表达式
sqrt(-4.0)进行计算时,结果会被认为是一个特殊值NaN(Not a Number),表示无效的操作。负数的平方根是一个虚数,在实数域中没有定义。
在你的机器上,整数除0和浮点数除0的运行结果各是什么?为什么会有不同的运行结果?,并将“-6.0/0”和“-6/0”的运行结果进行比较。
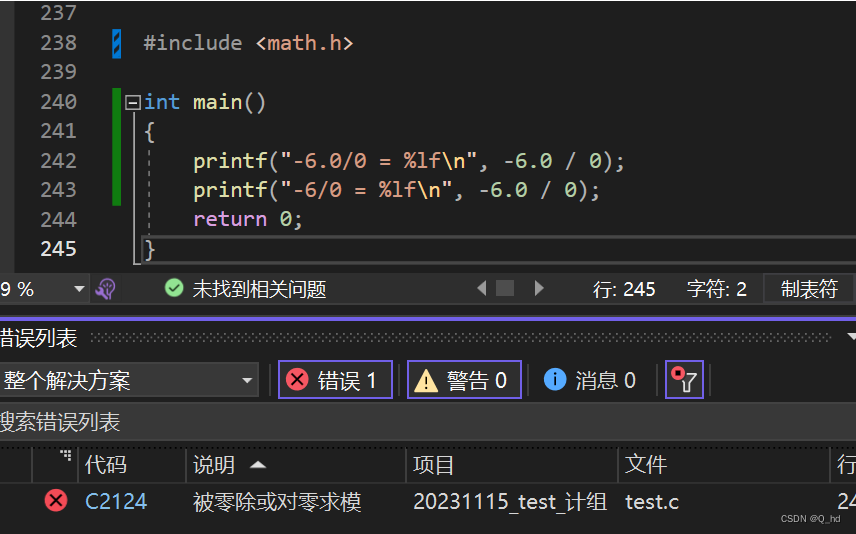
在VS中,错误C2124表示发生了除以零或求模运算中的被零除的情况。这个错误通常出现在编译时,是因为代码中存在了除以零或对零求模的操作,这是一种不合法的操作。
这个错误会阻止程序的继续编译,因为除以零是一种未定义的行为,违反了数学和计算机的基本规则。
要解决这个错误,你需要检查代码中是否存在除以零或对零求模的操作,并确保避免这种情况的发生。可以通过添加适当的条件判断来避免除以零或对零求模,在进行除法或求模运算之前检查除数是否为零。
例如,可以使用条件语句来避免除以零的情况:
if(b != 0) {result = a / b; // 在除数不为零时执行除法运算
}
else{// 处理除数为零的情况,例如输出错误信息或采取其他操作printf("除数不能为零\n");
}
结语
通过本文的分析,我们了解了C语言中数学运算和类型转换的一些关键细节。从取负运算到浮点数的精度,再到除零的处理,每个概念都对编写可靠和高效的代码至关重要。希望这篇文章能帮助你在未来的编程实践中避免一些常见的陷阱。
相关文章:

【C语言】深入理解C语言中的数学运算和类型转换
文章目录 引言取负运算的奥秘源码探索分析与解读 浮点数运算的精细差异源码分析精度损失与隐式类型转换 精度和除零运算探究float类型和double类型的精度各是多少(即十进制有效位的位数)?在你的机器上,“负数开方”是如何处理的&a…...
基于javaweb的宠物服务商城系统设计与开发
摘 要 最近几年以来,宠物在人们的日常生活中所占的地位越来越重要了,它们不仅仅是我们的朋友,也成为了我们家庭中的一份子。21世纪,信息技术飞速发展,计算机行业日新月异,极大地带动了信息的流动ÿ…...

LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】 题目描述:解题思路一:首先说一个结论就是(rand_X() - 1) Y rand_Y() > [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数…...

通达信指标公式19:龙虎榜股票池——主力控盘度的计算方法
0.小红牛本指标,选股的思路说明:控盘度,又称主力控盘,是指主力控制了某只股票的大部分流通股,从而控制了股票的价格。主力控盘的目的通常是为了获取更多的收益,通过控制股票价格来实现其策略。所以首要分析…...
手搓图片滑动验证码_JavaScript进阶
手搓图片滑动验证码 背景代码效果图展示网站 背景 在做前端项目开发的时候,少不了登录注册部分,既然有登录注册就少不了机器人验证,验证的方法有很多种,比如短信验证码、邮箱验证码、图片滑动、图片验证码等。 由于鄙人在开发中…...

Linux服务器超级实用的脚本
1.使用INOTIFY+RSYNC自动实时同步数据 代码执行: bash inotify_rsyncs.sh :cat inotify_rsyncs.sh 脚本内容如下: #!bing/bash # Author: reyn #检测/data路径下的文件变化,排除Temp目录 INOTIFY_CMD="inotifywait -mrq -e modify,create,move,delete /data/ --exc…...

IntelliJ IDEA安装使用教程#intellij idea
做为基础开发软件,idea、pycharm、phpstorm是高级企业级开发中常用的图形化工具。 安装非常简单:去官网下载即可,有社区版本、有企业版本: IntelliJ IDEA – 领先的 Java 和 Kotlin IDE 因版权问题:这里不方面多讲。…...
【组合数学】容斥鸽巢原理
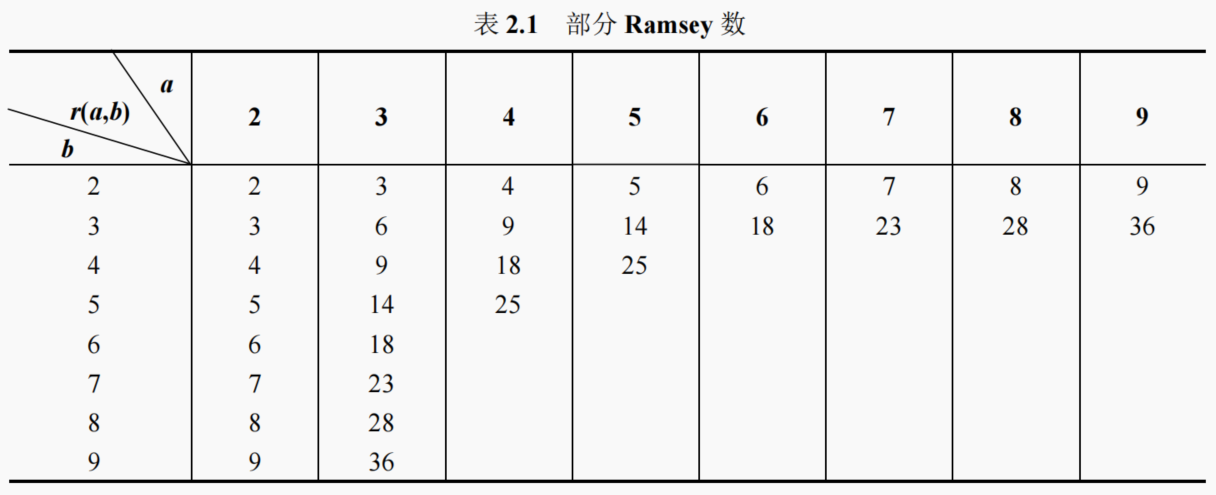
目录 1. 容斥原理容斥原理三种形式 2. 容斥原理应用有限重复数的多重集合的 r 组合数错排问题 3. 鸽巢原理4. Ramsey 定理 1. 容斥原理 容斥原理提供了一种通过计算每个单独集合的大小,然后修正重复计数的方法,从而得到多个集合并集大小的计算方法。它通…...
视频后期特效处理软件 Motion 5 mac中文版
Motion mac是一款运动图形和视频合成软件,适用于Mac OS平台。 Motion mac软件特点 - 精美的效果:Motion提供了多种高质量的运动图形和视频效果,例如3D效果、烟雾效果、粒子效果等,方便用户制作出丰富多彩的视频和动画。 - 高效的工…...

【智能家居】一、工厂模式实现继电器灯控制
用户手册对应的I/O 工厂模式实现继电器灯控制 代码段 controlDevice.h(设备设备)main.c(主函数)bathroomLight.c(浴室灯)bedroomLight.c(卧室灯)restaurantLight.c(餐厅…...
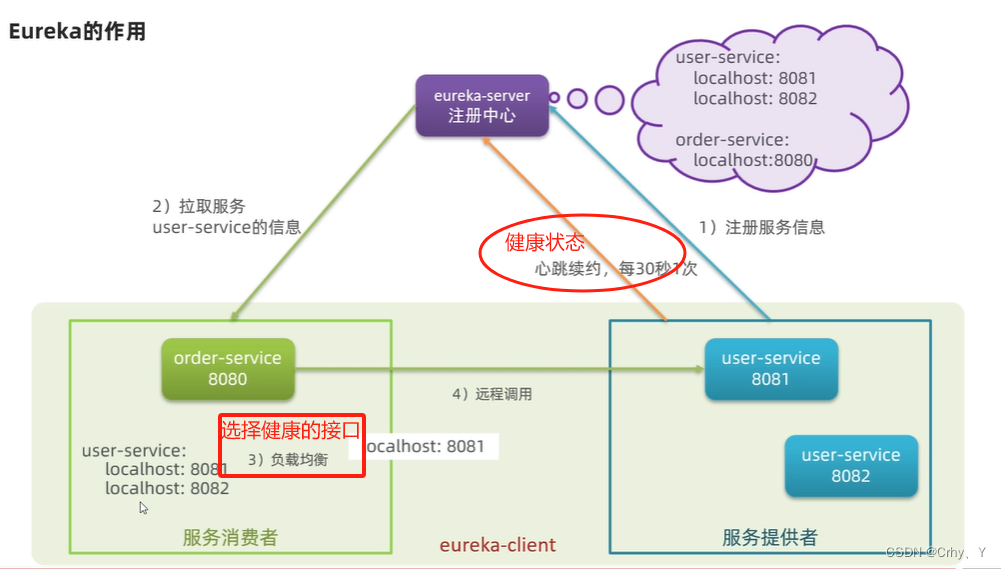
第三节:提供者、消费者、Eureka
一、 提供者 消费者(就是个说法、定义,以防别人叭叭时听不懂) 服务提供者:业务中被其他微服务调用的服务。(提供接口给其他服务调用)服务消费者:业务中调用其他微服务的服务。(调用…...
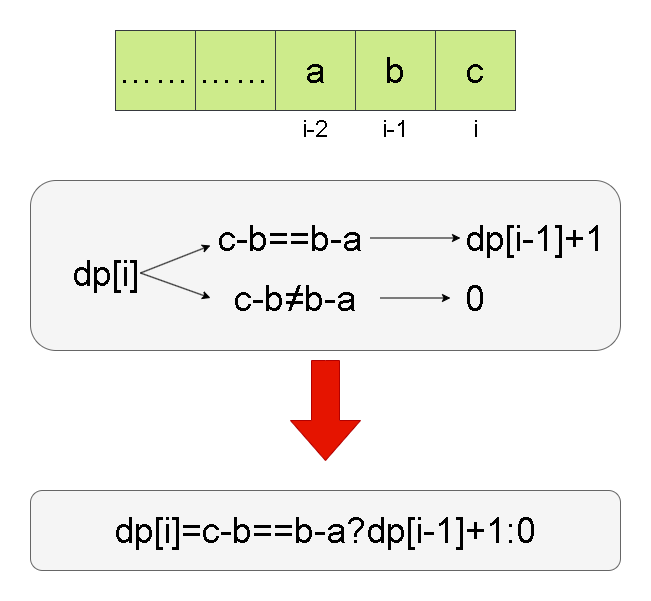
Leetcode刷题详解——等差数列划分
1. 题目链接:413. 等差数列划分 2. 题目描述: 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 …...

导出主机上所有docker 镜像并导入到其它主机
保存镜像列表到文件 docker images --format “{{.Repository}}:{{.Tag}}” > image_list.txt 导出列表中所有镜像到tar文件 cat image_list.txt | xargs -L 1 docker save -o all_images.tar 导入tar包中所有镜像 docker load -i all_images.tar...

HTML5+CSS3+JS小实例:焦点图波浪切换动画特效
实例:焦点图波浪切换动画特效 技术栈:HTML+CSS+JS 字体图标库:Font Awesome 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name=&…...
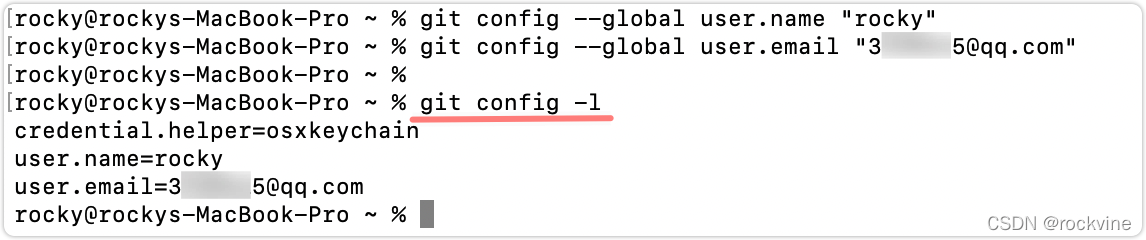
Mac电脑如何安装git
一、简介 在Mac上安装Git之前,可以先使用git --version来查看一下是否安装了Git,因为Mac系统可能自带了Git,或者在你安装XCode(或者XCode的命令行工具)时,可能已经安装了 Git。 如果Mac还没有安装Git的话&…...
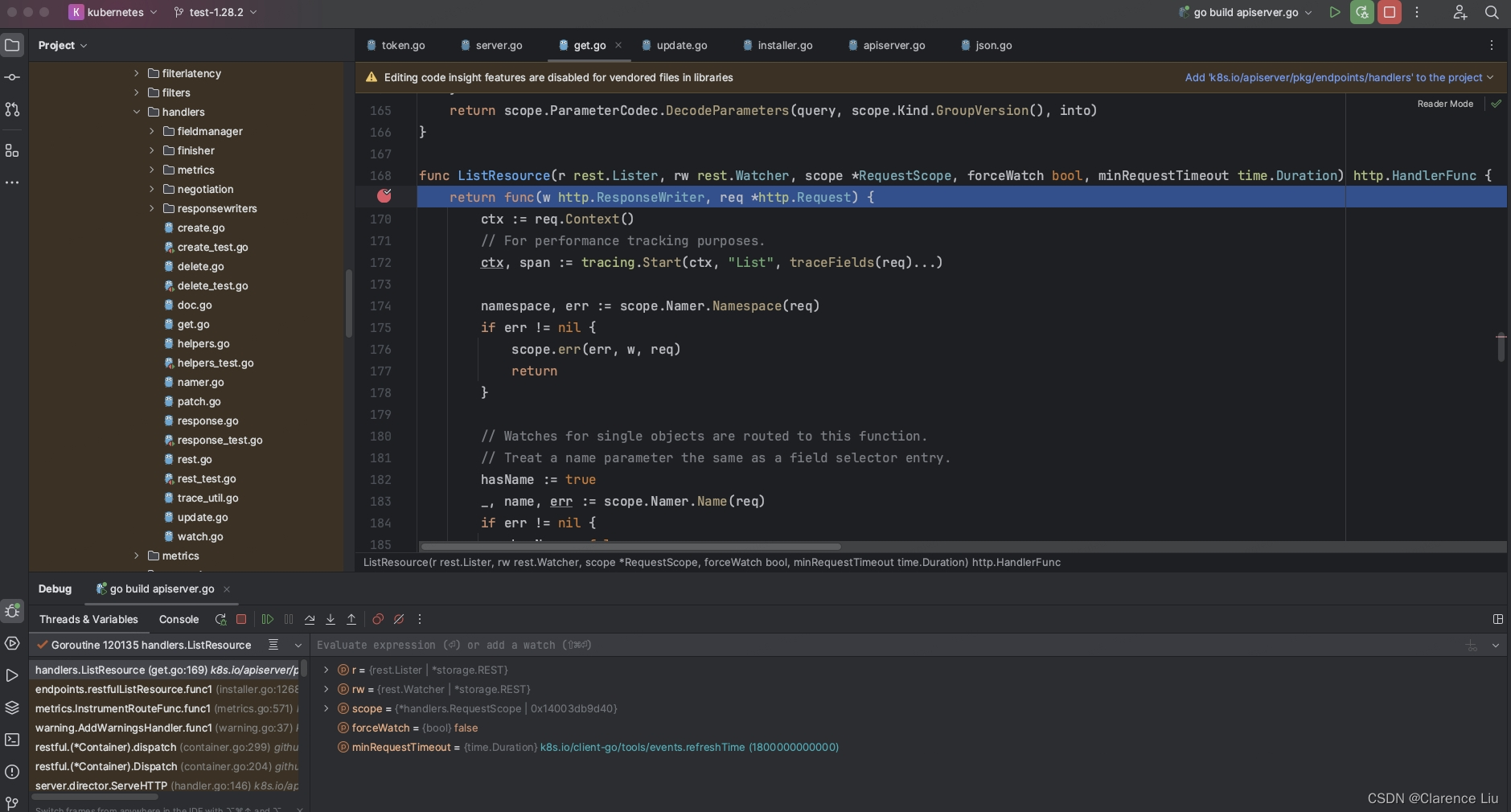
macOS本地调试k8s源码
目录 准备工作创建集群注意点1. kubeconfig未正常加载2. container runtime is not running3. The connection to the server 172.16.190.132:6443 was refused - did you specify the right host or port?4. 集群重置5.加入子节点 代码调试 准备工作 apple m1芯片 安装vmwa…...

JS 实现一键复制文本内容
1、演示: 2、代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>一键复制</title&g…...

【Linux】echo命令使用
echo命令 功能是在显示器上显示一段文字,一般起到一个提示的作用。此外,也可以直接在文件中写入要写的内容。也可以用于脚本编程时显示某一个变量的值,或者直接输出指定的字符串。 著者 由布莱恩福克斯和切特拉米撰写。 语法 echo […...

Day03 嵌入式---中断
目录 一、简单介绍 二、总体框架 三、NVIC 3.2 NVIC的寄存器 3.3 中断向量表 3.4 中断优先级 3.5 NVIC优先级分组 3.6 NVIC配置 3.6.1、设置中断分组 3.6.2、初始化 四、EXTI 外部中断 4.1.EXTI的基本概念 4.2.EXTI的⼯作原理 4.3 EXTI配置 五、SYSCFG 5.1 SYS…...
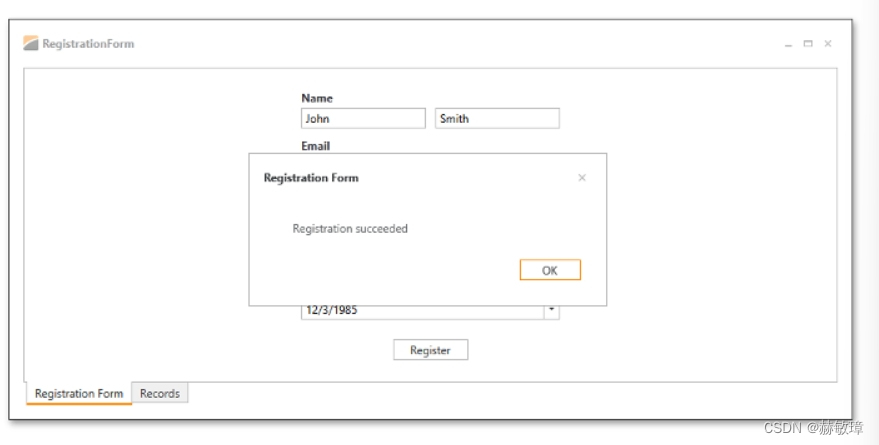
wpf devexpress 使用IDataErrorInfo实现input验证
此处下载源码 当form初始化显示,Register按钮应该启动和没有输入错误应该显示。如果用户点击注册按钮在特定的输入无效数据,form将显示输入错误和禁用的注册按钮。实现逻辑在标准的IDataErrorInfo接口。请查阅IDataErrorInfo接口(System.Com…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
