LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】
- 题目描述:
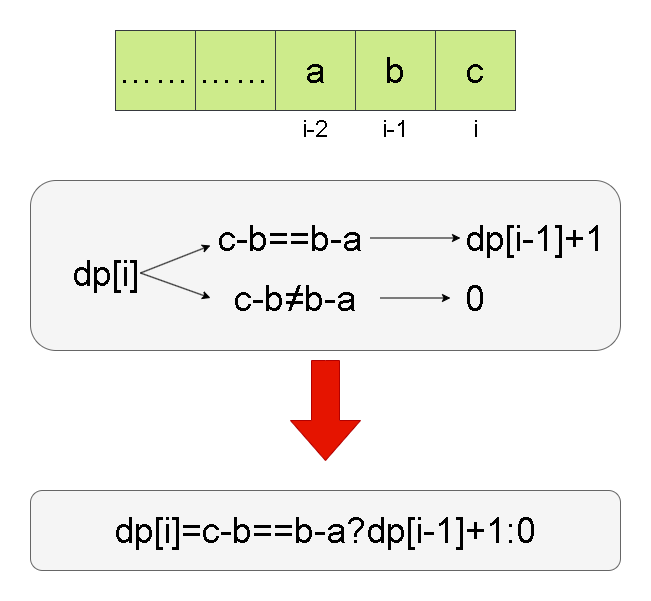
- 解题思路一:首先说一个结论就是`(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y]`,即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用`(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]`得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即`if num<=40:`才进行采样。
- 解题思路二:0
- 解题思路三:0
题目描述:
给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数,试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。
你只能调用 rand7() 且不能调用其他方法。请不要使用系统的 Math.random() 方法。
每个测试用例将有一个内部参数 n,即你实现的函数 rand10() 在测试时将被调用的次数。请注意,这不是传递给 rand10() 的参数。
示例 1:
输入: 1
输出: [2]
示例 2:
输入: 2
输出: [2,8]
示例 3:
输入: 3
输出: [3,8,10]
提示:
1 <= n <= 105
进阶:
rand7()调用次数的 期望值 是多少 ?
你能否尽量少调用 rand7() ?
解题思路一:首先说一个结论就是(rand_X() - 1) × Y + rand_Y() ==> [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数,Y是每一行的人数,X是列数【参考下面的图】。第二就是拒绝采样,效果是能够减少调用rand7()的调用次数。我们在利用(rand_7() - 1) × 7 + rand_7() ==> [1,7*7]得到rand49()的时候,我们希望能够等概率的生成[1,10]的随机数,那么可以拒绝掉大于40的数。即if num<=40:才进行采样。

为了充分利用被拒绝的采样结果,即舍弃掉[41, 49]这9个数。我们可以使用a = num - 40得到rand9,从而可以得到(rand_9() - 1) × 7 + rand_7() ==> [1,9*7]得到rand63,从而对rand63进行采样。这样之后的就不难理解了。
# The rand7() API is already defined for you.
# def rand7():
# @return a random integer in the range 1 to 7class Solution:def rand10(self):""":rtype: int"""while True:a = rand7()b = rand7()num = (a-1)*7 + b # rand49if num<=40:return num%10 + 1a = num - 40 # rand9b = rand7()num = (a-1)*7 + b # rand63if num<=60:return num%10 + 1a = num - 60 # rand3b = rand7()num = (a-1)*7 + b # rand21if num<=20:return num%10 + 1
时间复杂度:期望时间复杂度为O(1),但最坏情况下会达到 (∞)(一直被拒绝)。
空间复杂度:O(1)
分析一下rand7()调用次数的 期望值:
首先调用2次得到a,b
然后拒绝采样一次概率是9/49
第二次是9/49 * 3/63
第三次是9/49 * 3/63 * 1/21就是进入下一轮while循环了。所以是一个等比数列。
a = 2 + 9 49 + 9 49 ⋅ 3 63 / / 是每次采样成功的概率 b = 9 49 ⋅ 3 63 ⋅ 1 21 / / 是每次进入下一轮循环的概率(等比数列的公比) E ( # c a l l ) = a ⋅ 1 1 − b ≈ 2.19333 \begin{align} a &= 2 + \frac{9}{49}+\frac{9}{49}·\frac{3}{63} \quad // \text{是每次采样成功的概率} \notag \\ b &= \frac{9}{49}·\frac{3}{63}·\frac{1}{21} \quad // \text {是每次进入下一轮循环的概率(等比数列的公比)} \notag \\ E(\#call) &= a·\frac{1}{1-b} \notag \\ &\approx 2.19333 \end{align} abE(#call)=2+499+499⋅633//是每次采样成功的概率=499⋅633⋅211//是每次进入下一轮循环的概率(等比数列的公比)=a⋅1−b1≈2.19333
所以期望次数是2.19332
解题思路二:0
解题思路三:0
相关文章:

LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】 题目描述:解题思路一:首先说一个结论就是(rand_X() - 1) Y rand_Y() > [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数…...

通达信指标公式19:龙虎榜股票池——主力控盘度的计算方法
0.小红牛本指标,选股的思路说明:控盘度,又称主力控盘,是指主力控制了某只股票的大部分流通股,从而控制了股票的价格。主力控盘的目的通常是为了获取更多的收益,通过控制股票价格来实现其策略。所以首要分析…...
手搓图片滑动验证码_JavaScript进阶
手搓图片滑动验证码 背景代码效果图展示网站 背景 在做前端项目开发的时候,少不了登录注册部分,既然有登录注册就少不了机器人验证,验证的方法有很多种,比如短信验证码、邮箱验证码、图片滑动、图片验证码等。 由于鄙人在开发中…...

Linux服务器超级实用的脚本
1.使用INOTIFY+RSYNC自动实时同步数据 代码执行: bash inotify_rsyncs.sh :cat inotify_rsyncs.sh 脚本内容如下: #!bing/bash # Author: reyn #检测/data路径下的文件变化,排除Temp目录 INOTIFY_CMD="inotifywait -mrq -e modify,create,move,delete /data/ --exc…...

IntelliJ IDEA安装使用教程#intellij idea
做为基础开发软件,idea、pycharm、phpstorm是高级企业级开发中常用的图形化工具。 安装非常简单:去官网下载即可,有社区版本、有企业版本: IntelliJ IDEA – 领先的 Java 和 Kotlin IDE 因版权问题:这里不方面多讲。…...
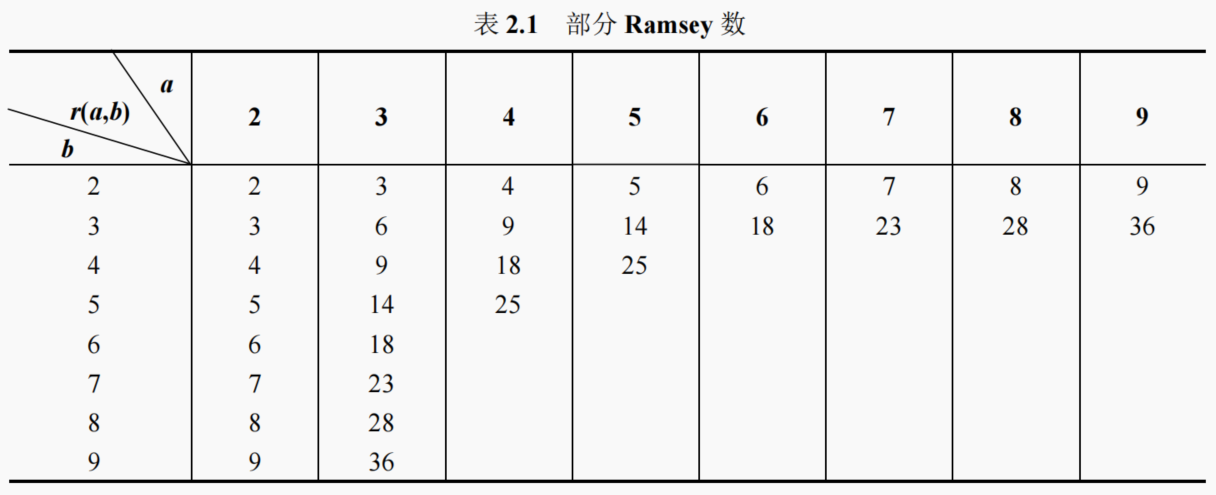
【组合数学】容斥鸽巢原理
目录 1. 容斥原理容斥原理三种形式 2. 容斥原理应用有限重复数的多重集合的 r 组合数错排问题 3. 鸽巢原理4. Ramsey 定理 1. 容斥原理 容斥原理提供了一种通过计算每个单独集合的大小,然后修正重复计数的方法,从而得到多个集合并集大小的计算方法。它通…...
视频后期特效处理软件 Motion 5 mac中文版
Motion mac是一款运动图形和视频合成软件,适用于Mac OS平台。 Motion mac软件特点 - 精美的效果:Motion提供了多种高质量的运动图形和视频效果,例如3D效果、烟雾效果、粒子效果等,方便用户制作出丰富多彩的视频和动画。 - 高效的工…...

【智能家居】一、工厂模式实现继电器灯控制
用户手册对应的I/O 工厂模式实现继电器灯控制 代码段 controlDevice.h(设备设备)main.c(主函数)bathroomLight.c(浴室灯)bedroomLight.c(卧室灯)restaurantLight.c(餐厅…...
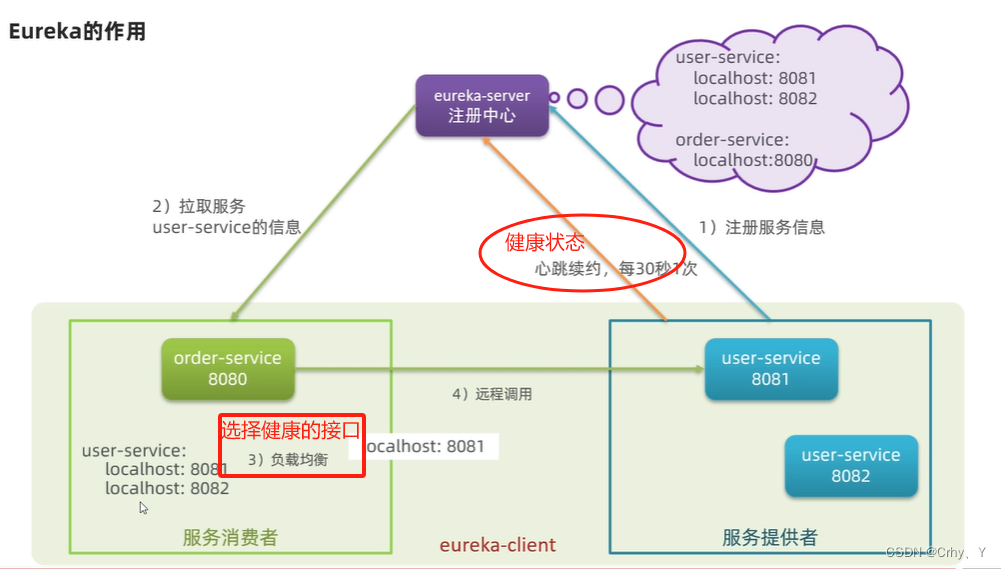
第三节:提供者、消费者、Eureka
一、 提供者 消费者(就是个说法、定义,以防别人叭叭时听不懂) 服务提供者:业务中被其他微服务调用的服务。(提供接口给其他服务调用)服务消费者:业务中调用其他微服务的服务。(调用…...
Leetcode刷题详解——等差数列划分
1. 题目链接:413. 等差数列划分 2. 题目描述: 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 …...

导出主机上所有docker 镜像并导入到其它主机
保存镜像列表到文件 docker images --format “{{.Repository}}:{{.Tag}}” > image_list.txt 导出列表中所有镜像到tar文件 cat image_list.txt | xargs -L 1 docker save -o all_images.tar 导入tar包中所有镜像 docker load -i all_images.tar...

HTML5+CSS3+JS小实例:焦点图波浪切换动画特效
实例:焦点图波浪切换动画特效 技术栈:HTML+CSS+JS 字体图标库:Font Awesome 效果: 源码: 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name=&…...
Mac电脑如何安装git
一、简介 在Mac上安装Git之前,可以先使用git --version来查看一下是否安装了Git,因为Mac系统可能自带了Git,或者在你安装XCode(或者XCode的命令行工具)时,可能已经安装了 Git。 如果Mac还没有安装Git的话&…...
macOS本地调试k8s源码
目录 准备工作创建集群注意点1. kubeconfig未正常加载2. container runtime is not running3. The connection to the server 172.16.190.132:6443 was refused - did you specify the right host or port?4. 集群重置5.加入子节点 代码调试 准备工作 apple m1芯片 安装vmwa…...

JS 实现一键复制文本内容
1、演示: 2、代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>一键复制</title&g…...

【Linux】echo命令使用
echo命令 功能是在显示器上显示一段文字,一般起到一个提示的作用。此外,也可以直接在文件中写入要写的内容。也可以用于脚本编程时显示某一个变量的值,或者直接输出指定的字符串。 著者 由布莱恩福克斯和切特拉米撰写。 语法 echo […...

Day03 嵌入式---中断
目录 一、简单介绍 二、总体框架 三、NVIC 3.2 NVIC的寄存器 3.3 中断向量表 3.4 中断优先级 3.5 NVIC优先级分组 3.6 NVIC配置 3.6.1、设置中断分组 3.6.2、初始化 四、EXTI 外部中断 4.1.EXTI的基本概念 4.2.EXTI的⼯作原理 4.3 EXTI配置 五、SYSCFG 5.1 SYS…...
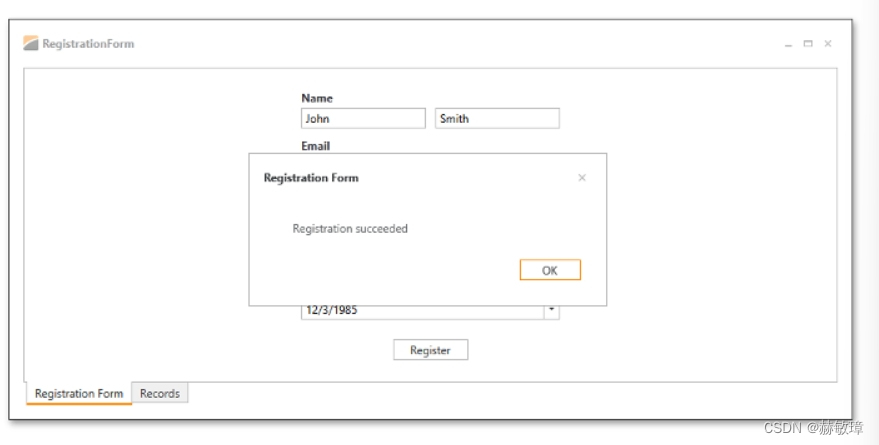
wpf devexpress 使用IDataErrorInfo实现input验证
此处下载源码 当form初始化显示,Register按钮应该启动和没有输入错误应该显示。如果用户点击注册按钮在特定的输入无效数据,form将显示输入错误和禁用的注册按钮。实现逻辑在标准的IDataErrorInfo接口。请查阅IDataErrorInfo接口(System.Com…...

shell_81.Linux在命令行中创建使用函数
在命令行中使用函数 在命令行中创建函数 两种方法 单行方式来定义函数: $ function divem { echo $[ $1 / $2 ]; } $ divem 100 5 20 $ 当你在命令行中定义函数时,必须在每个命令后面加个分号,这样 shell 就能知道哪里是命令的起止了&am…...
)
鱼香ROS一键安装命令(支持微信、docker、ros等)
按照指定的数字选择即可。 wget http://fishros.com/install -O fishros && . fishros小鱼的一键安装系列 [14个ROS版本任你选]一键安装Docker使用指南...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
