LeetCode算法复杂度分析(时间复杂度空间复杂度)
文章目录
- 前言
- 时间复杂度
- 1.概述
- 2.大O记法
- 3.常见类型
- 空间复杂度
- 1.概述
- 2.常见类型
- 典型算法的复杂度分析
- 1.递归算法
- 2.哈希表
前言
我们知道,研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求。
时间复杂度
1.概述
我们要计算算法时间耗费情况,但我们并不能将时间占用和空间占用量化。所以我们得度量算法的执行时间,那么如何度量呢?
我们分析一个算法的运行时间,最重要的就是把核心操作的次数和输入规模关联起来。
2.大O记法
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况并确定T(n)的量级。
算法的时间复杂度,就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称时间复杂度,其中f(n)是问题规模n的某个函数。
所以计算时间复杂度主要分两步:统计操作数量&判断渐进上界
常用技巧:
(1)用常数1取代运行时间中的所有加法常数;
(2)在修改后的运行次数中,只保留高阶项;
(3)如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数;
3.常见类型
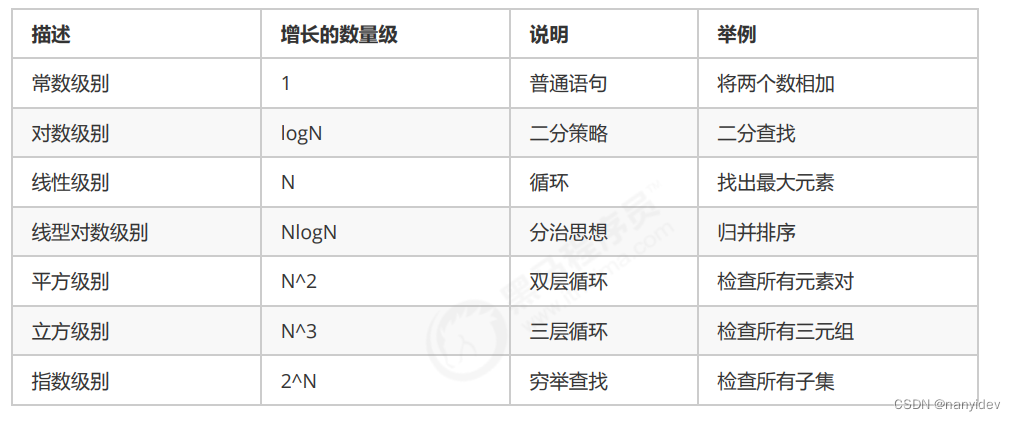
首先,常见的时间复杂度类型排序:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2) <O(2^n) <O(n!)
空间复杂度
1.概述
统计 算法使用内存空间随着数据量变大时的增长趋势.
通常情况下,空间复杂度统计范围是「暂存空间」+「输出空间」
2.常见类型
同样是用大O来表示,只是这个是表示使用空间大小
O(1)<O(logn)<O(n)<O(n^2) <O(2^n)
典型算法的复杂度分析
1.递归算法
(1)时间复杂度
子问题个数乘以解决一个子问题需要的时间(即递归的次数 * 每次递归中的操作次数。)
例如,斐波那契数列
(2)空间复杂度
2.哈希表
空间换时间,查找的时间复杂度是O(1)
参考链接:https://www.helloalgo.com/chapter_computational_complexity/space_complexity/#232
https://programmercarl.com
相关文章:

LeetCode算法复杂度分析(时间复杂度空间复杂度)
文章目录前言时间复杂度1.概述2.大O记法3.常见类型空间复杂度1.概述2.常见类型典型算法的复杂度分析1.递归算法2.哈希表前言 我们知道,研究算法的最终目的就是如何花更少的时间,如何占用更少的内存去完成相同的需求。 时间复杂度 1.概述 我们要计算算…...
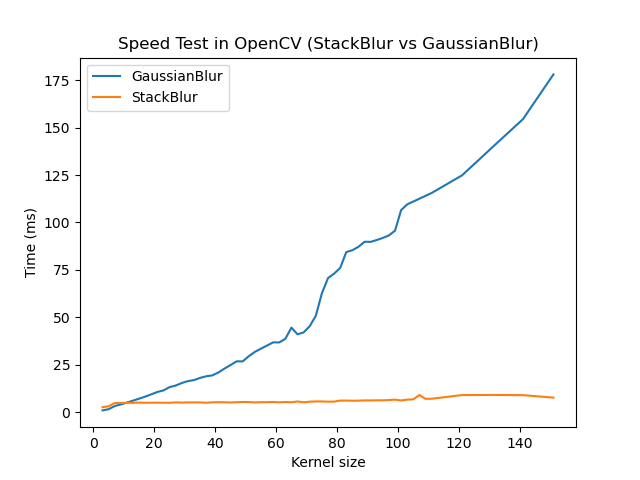
Android OpenCV(七十三):吊打高斯模糊的StackBlur Android 实践
前言 OpenCV 4.7.0 2022年12月28日Release,ChangeLog中提到 Stackblur algorithm implementation. Stackblur是一种高斯模糊的快速近似,由Mario Klingemann发明。其计算耗时不会随着kernel size的增大而增加,专为大kernel size的模糊滤波场景量身定制。 使用建议:当kerne…...

4.排序算法之一:冒泡排序
排序算法稳定性假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]r[j],且r[i]在r[j]之前,而在排序后的序列中,r[…...

python自学之《21天学通Python》(16)——第19章 用Pillow库处理图片
Pillow是Python2.X时代比较流行的Python ImagingLibrary(简称Pillow)图像处理库的分支,并修复了一些bug。Pillow提供了对Python3的支持,为Python3解释器提供了图像处理的功能。和Pillow库一样提供了广泛的文件格式支持、高效的内部…...
发布依赖到maven仓库
maven中央仓库是一个开放的仓库,所以我们也可以把自己开发的jar推送到远程仓库,这样可以直接引入pom依赖使用我们的库。 准备工作 ● 需要一个github账号(程序员必备) ● 网络代理(涉及到的网站通常没版本在国内直接访…...
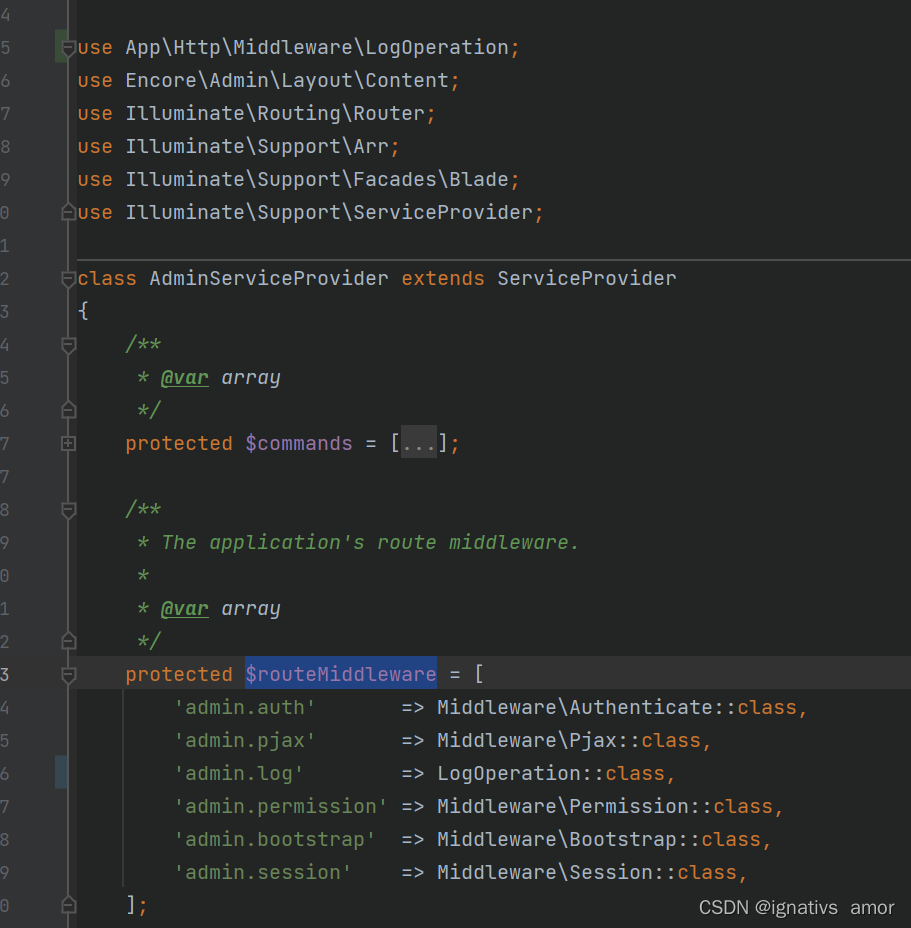
Laravel-admin之自定义操作日志
laravel-admin是封装性极好的框架,自带的就有操作日志的记录,但是对于非开发人员可能看不懂这个日志,所以就想着给修改一下,以谁修改了什么,谁删除了什么,谁审核了什么,谁添加了什么类似&#x…...

用Python做了一个法律查询小工具,非常好用
用Python做了一个法律查询小工具,非常好用效果展示准备工作不会的话可以点我直达代码和视频讲解,我都准备好了主要代码哈喽兄弟,今天给大家分享一个Python tkinter制作法律查询小工具。 光爬虫大家也只能自己用用,就算打包了exe&…...
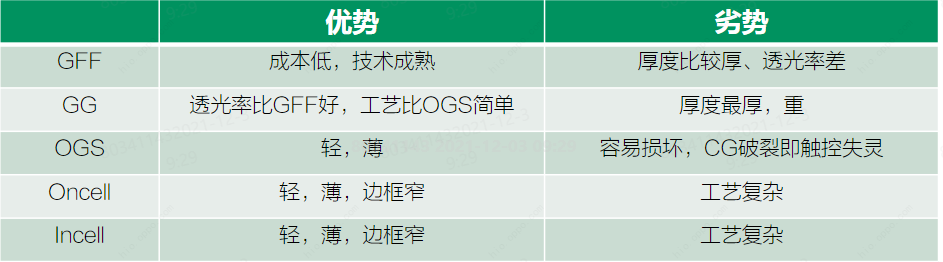
工作篇:触摸屏原理介绍
一、触摸屏概述 触摸屏作为一种新的输入设备,它是目前最简单、方便、自然的一种人机交互方式。 当接触了屏幕上的图形按钮时,屏幕上的触觉反馈系统可根据预先编程的程式驱动各种连结装置,可用以取代机械式的按钮面板,并借由液晶…...
Ep_操作系统面试题-操作系统的分类
答案 单体系统 整个操作系统是以程序集合来编写的,链接在一块形成一个二进制可执行程序,这种系统称为单体系统。 分层系统 每一层都使用下面的层来执行其功能。 微内核 微内核架构的内核只保留最基本的能力,把一些应用放到了用户空间 客户-…...

iframe或document监听滚动事件不起作用
有时候我们会遇到监听iframe或document的滚动事件不起作用的情况,在排除代码写错的情况下,我们应该考虑此时的document是否可以滑动。 1、为什么document不能监听滑动? 就很奇怪,明明页面时有滚动条的,为什么说document不可滑动…...
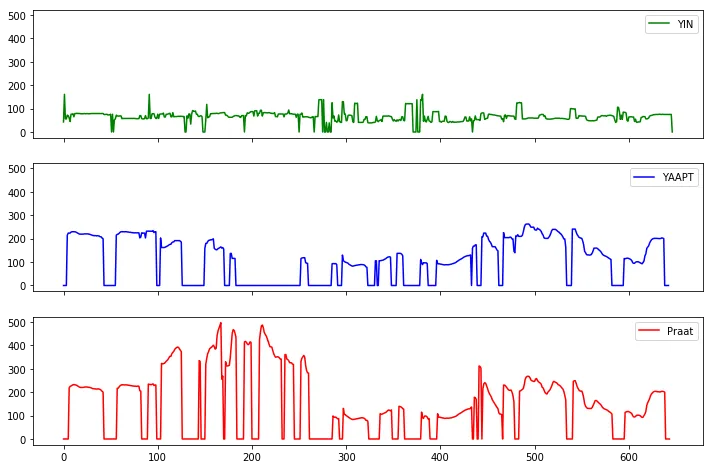
基频估计算法简介
基频估计算法 F0 estimate methods 估计F0的方法可以分为三类:基于时域、基于频域、或混合方法。本文详细介绍了这些方法。 所有的算法都包含如下三个主要步骤: 1.预处理:滤波,加窗分帧等 2.搜寻:可能的基频值F0(候选…...

linux修改DNS 系统版本Kylin V10桌面版
配置DNS在银河麒麟桌面操作系统V10 SP1 中修改DNS信息,直接修改/etc/resolv.conf文件中的DNS信息,不能生效。应该参考如下步骤:一、首先修改 /etc/systemd/resolved.conf文件,在其中添加DNS信息在终端中执行以下命令:s…...

如何使用 AWS Lambda 运行 selenium
借助 AWS Lambda 运行 selenium 来爬取网络数据。 简介 与手动从网站收集数据相比,爬虫可以为我们节省很多时间,对于爬虫的每次请求而言,这相当于 AWS Lambda 的每次函数的运行。 AWS Lambda 是一种将脚本部署到云的简单且价格低廉的服务&…...
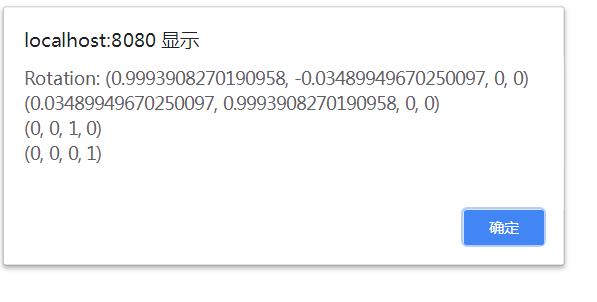
认识Cesium旋转大小变量
前文代码中有如下;矩阵乘以旋转大小,还放入mat; Cesium.Matrix4.multiply(mat, rotationX, mat); 初看以为rotationX是一个数值,因为矩阵可以和数相乘; 但是看它的代码,rotationX是由一长串代码获得的&a…...

异响加持、吐槽声不断,小鹏G9难解困局
小鹏汽车的烦恼就好比红尘中的三千青丝,小鹏G9“惊魂48小时”的恐慌还未平息,车门异响等问题就已经层出不穷,再次将小鹏汽车推上风口浪尖。 可以毫不客气的说,G9承载着小鹏汽车盈利的希望,但在原本处于上升之势的G9却…...

【react】react18的学习
一、安装 $ create-react-app [Project name]默认支持sass 二、核心依赖 react:react 核心 react-dom:用于开发渲染web 应用; react-scripts:封装webpack服务; "start": "react-scripts start&quo…...

Ep_操作系统面试题-什么是线程,线程和进程的区别
1. 一个进程中可以有多个线程,多个线程共享进程的堆和方法区 (JDK1.8 之后的元空间),但是每个线程有自己的程序计数器、虚拟机栈和 本地方法栈。 2.进程是资源分配的最小单位,线程是CPU调度的最小单位 视频讲解: https://edu.csdn.net/course/detail/38090 点我…...

最流行的自动化测试工具,总有一款适合你(附部分教程)
前言 在自动化测试领域,自动化工具的核心地位毋庸置疑。本文总结了最顶尖的自动化测试工具和框架,这些工具和框架可以帮助组织更好地定位自己,跟上软件测试的趋势。这份清单包含了开源和商业的自动化测试解决方案。 1)Selenium …...

Shell高级——进程替换vs管道
以下内容源于C语言中文网的学习与整理,如有侵权请告知删除。 1、问题引入 这里将Shell中的“进程替换”与“管道”放在一起讲,是因为两者的作用几乎类似。 进程替换:将一个命令的输出结果传递给另一个(组)命令。 管…...
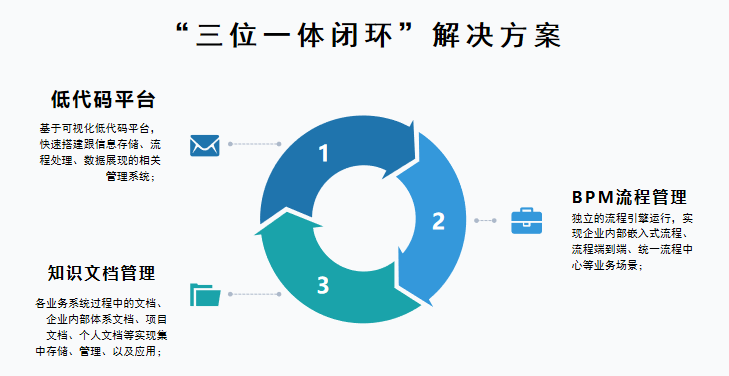
国内有哪些支持定制化的低代码平台?
编者按:贴合企业业务需求的系统才是好系统,高程度的定制能力平台意味着可以提供更高契合度的产品,更好地匹配业务需求。本文介绍了国内支持定制化的老厂商低代码平台,具有源码交付、私有化部署、国产化、数据对接等优势。关键词&a…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

react菜单,动态绑定点击事件,菜单分离出去单独的js文件,Ant框架
1、菜单文件treeTop.js // 顶部菜单 import { AppstoreOutlined, SettingOutlined } from ant-design/icons; // 定义菜单项数据 const treeTop [{label: Docker管理,key: 1,icon: <AppstoreOutlined />,url:"/docker/index"},{label: 权限管理,key: 2,icon:…...

VSCode 使用CMake 构建 Qt 5 窗口程序
首先,目录结构如下图: 运行效果: cmake -B build cmake --build build 运行: windeployqt.exe F:\testQt5\build\Debug\app.exe main.cpp #include "mainwindow.h"#include <QAppli...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...
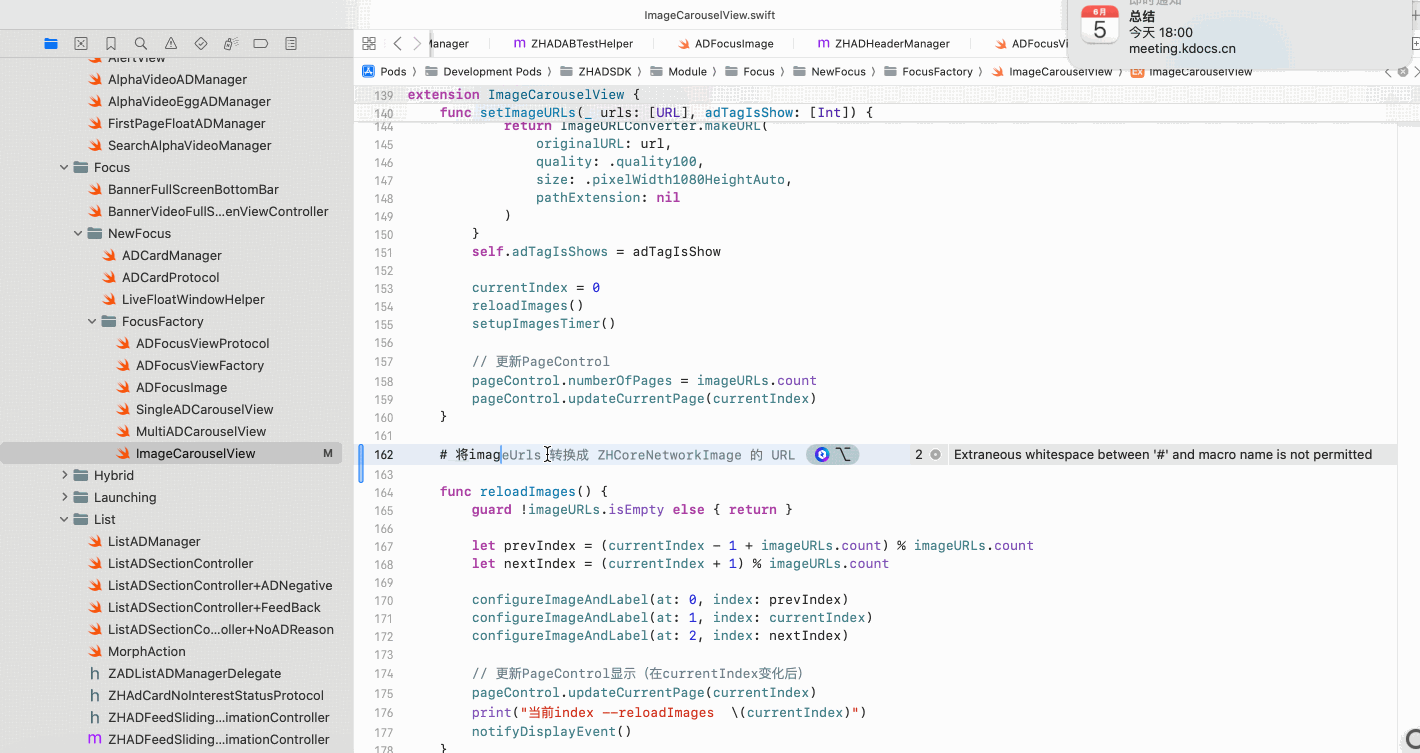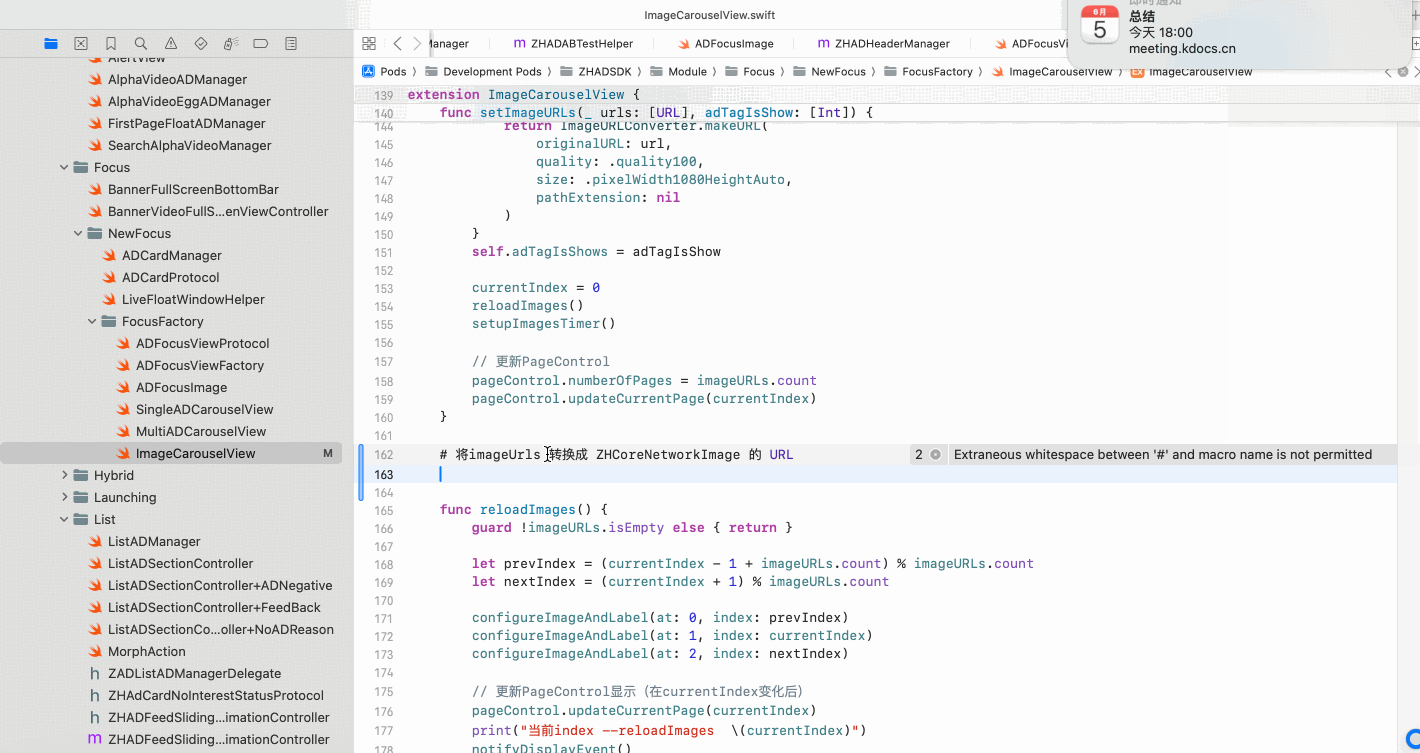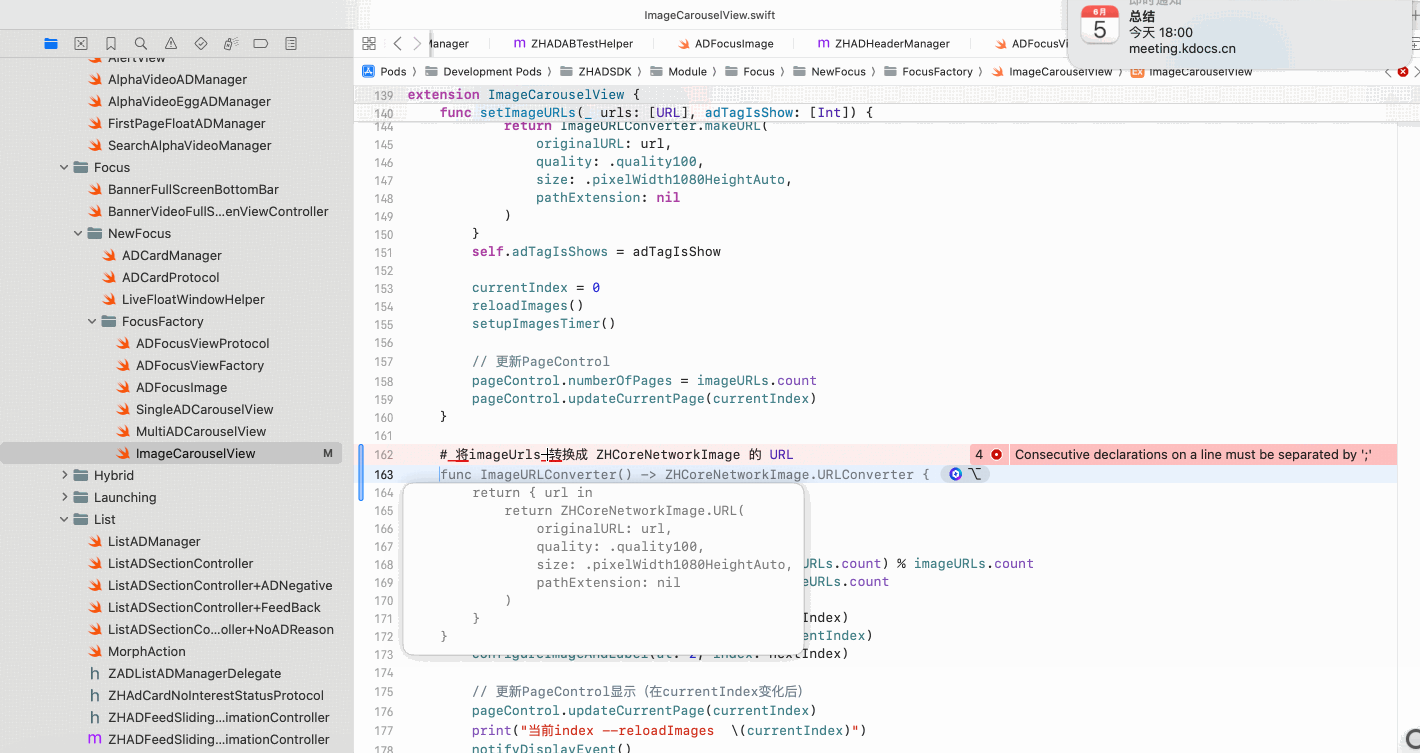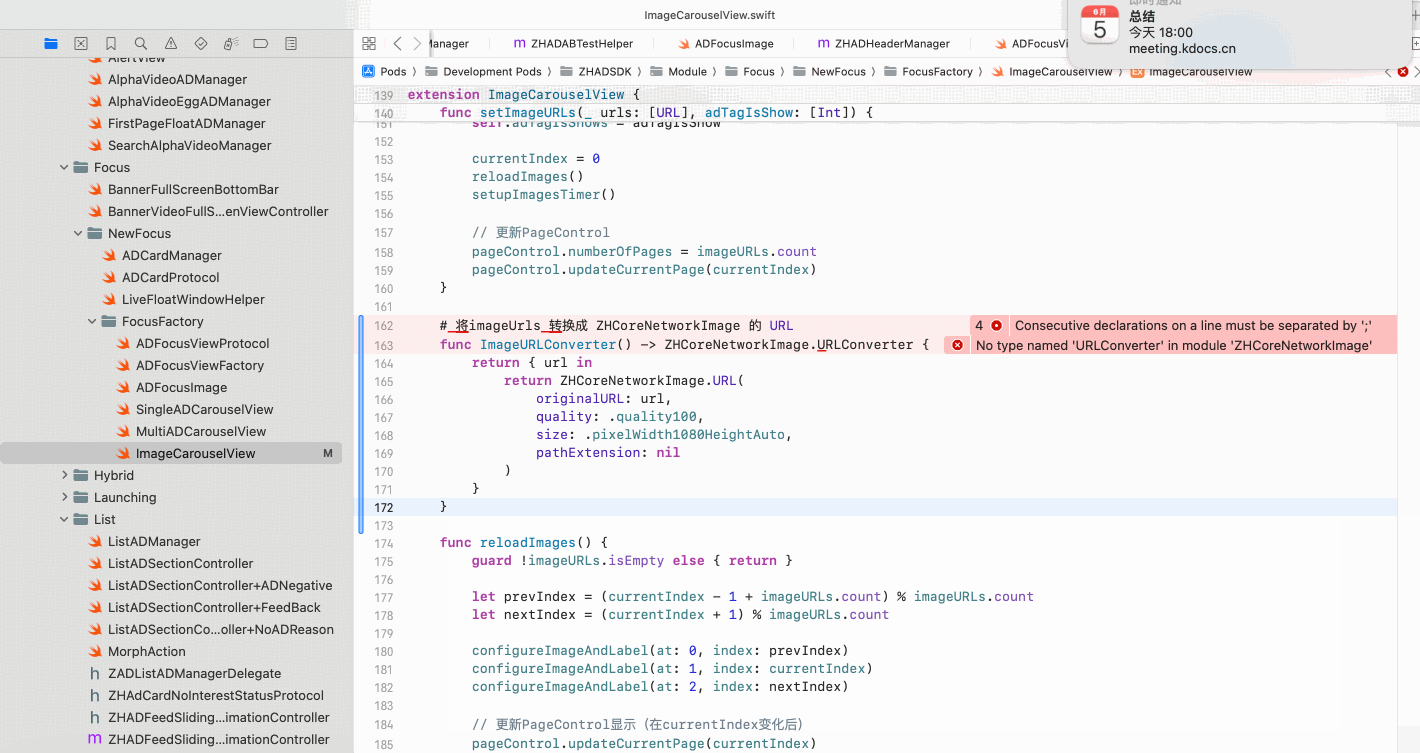
Copilot for Xcode (iOS的 AI辅助编程)
Copilot for Xcode 简介Copilot下载与安装 体验环境要求下载最新的安装包安装登录系统权限设置 AI辅助编程生成注释代码补全简单需求代码生成辅助编程行间代码生成注释联想 代码生成 总结 简介 尝试使用了Copilot,它能根据上下文补全代码,快速生成常用…...
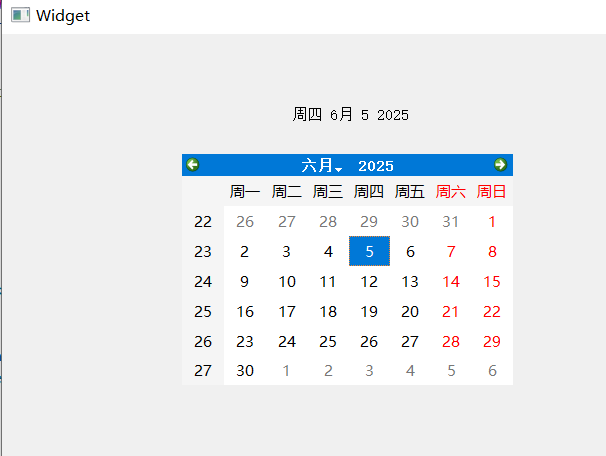
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
