Leetcode.2477 到达首都的最少油耗
题目链接
Leetcode.2477 到达首都的最少油耗
rating : 2012
题目描述
给你一棵 n n n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 0 0 到 n − 1 n - 1 n−1 ,且恰好有 n − 1 n - 1 n−1 条路。 0 0 0 是首都。给你一个二维整数数组 r o a d s roads roads ,其中 r o a d s [ i ] = [ a i , b i ] roads[i] = [a_i, b_i] roads[i]=[ai,bi] ,表示城市 a i a_i ai 和 b i b_i bi 之间有一条 双向路 。
每个城市里有一个代表,他们都要去首都参加一个会议。
每座城市里有一辆车。给你一个整数 s e a t s seats seats 表示每辆车里面座位的数目。
城市里的代表可以选择乘坐所在城市的车,或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。
请你返回到达首都最少需要多少升汽油。
示例 1:
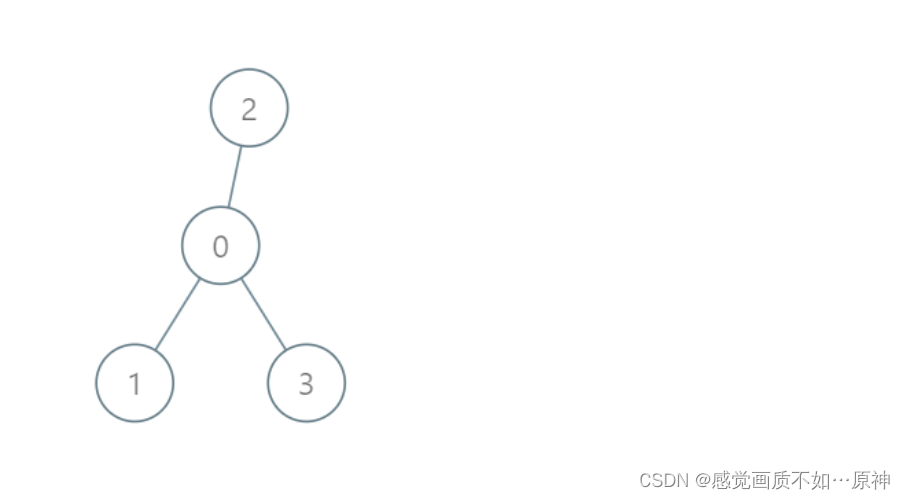
输入:roads = [[0,1],[0,2],[0,3]], seats = 5
输出:3
解释:
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 2 直接到达首都,消耗 1 升汽油。
- 代表 3 直接到达首都,消耗 1 升汽油。 最少消耗 3 升汽油。
示例 2:
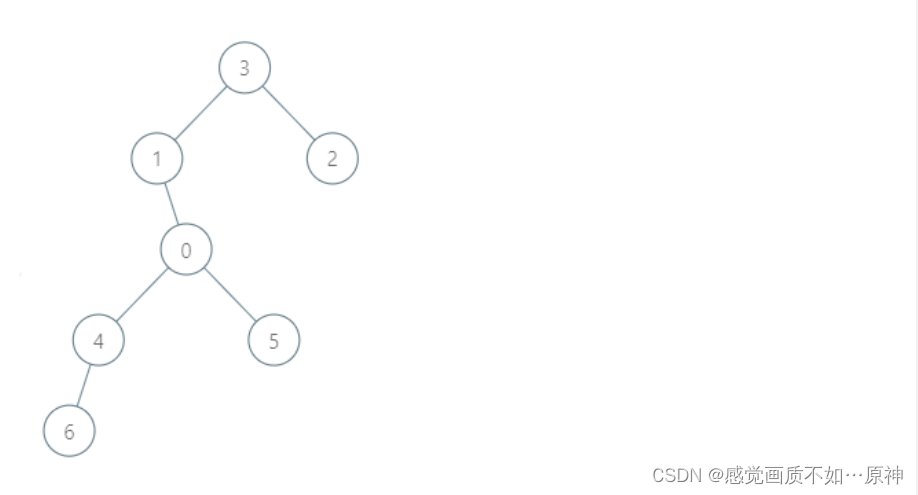
输入:roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出:7
解释:
- 代表 2 到达城市 3 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ,消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都,消耗 1 升汽油。
- 代表 1 直接到达首都,消耗 1 升汽油。
- 代表 5 直接到达首都,消耗 1 升汽油。
- 代表 6 到达城市 4 ,消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都,消耗 1 升汽油。 最少消耗 7 升汽油。
示例 3:

输入:roads = [], seats = 1
输出:0
解释:没有代表需要从别的城市到达首都。
提示:
- 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105
- r o a d s . l e n g t h = n − 1 roads.length = n - 1 roads.length=n−1
- r o a d s [ i ] . l e n g t h = 2 roads[i].length = 2 roads[i].length=2
- 0 ≤ a i , b i < n 0 \leq a_i, b_i < n 0≤ai,bi<n
- a i ≠ b i a_i \neq b_i ai=bi
- r o a d s roads roads 表示一棵合法的树。
- 1 ≤ s e a t s ≤ 1 0 5 1 \leq seats \leq 10^5 1≤seats≤105
解法:dfs + 贪心
越靠近起点 0 0 0 的边,经过的车越多,所消耗的燃料也就越多。
由于我们求得是消耗的最少的燃料,假设以点 v v v 为根节点的子树上的所有节点都要经过边 { u , v } \{ u,v\} {u,v} 到点 u u u,子树 v v v 的节点总数为 c n t v cnt_v cntv,那么要让 c n t v cnt_v cntv 个节点都被移动到 点 u u u ,最少需要 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车,为了用尽可能少的燃料,所以我们直接用 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车。
那么对于 边 { u , v } \{ u,v\} {u,v},一共有 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 辆车通过了这条边,所以一共要消耗 ⌈ c n t v s e a t s ⌉ \lceil \frac{cnt_v}{seats} \rceil ⌈seatscntv⌉ 升燃料。
我们直接从 起点 0 0 0 开始遍历所有的边,记录总的燃料即可。
时间复杂度 : O ( n ) O(n) O(n)
C++代码:
using LL = long long;class Solution {
public:long long minimumFuelCost(vector<vector<int>>& roads, int seats) {unordered_map<int,vector<int>> g;int n = 0;for(auto &e:roads){int a = e[0] , b = e[1];n = max({a,b,n});g[a].push_back(b);g[b].push_back(a);}n++;//s[i] 就是以 i 为根节点的节点总数vector<int> s(n);LL ans = 0;function<int(int,int)> dfs = [&](int u,int fa) ->int{s[u] = 1;for(auto v:g[u]){if(v == fa) continue;s[u] += dfs(v,u);}//不统计根节点if(u != 0) ans += (s[u] + seats - 1) / seats;return s[u];};dfs(0,-1);return ans;}
};
相关文章:

Leetcode.2477 到达首都的最少油耗
题目链接 Leetcode.2477 到达首都的最少油耗 rating : 2012 题目描述 给你一棵 n n n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 0 0 到 n − 1 n - 1 n−1 ,且恰好有 n − 1 n - 1 n−…...
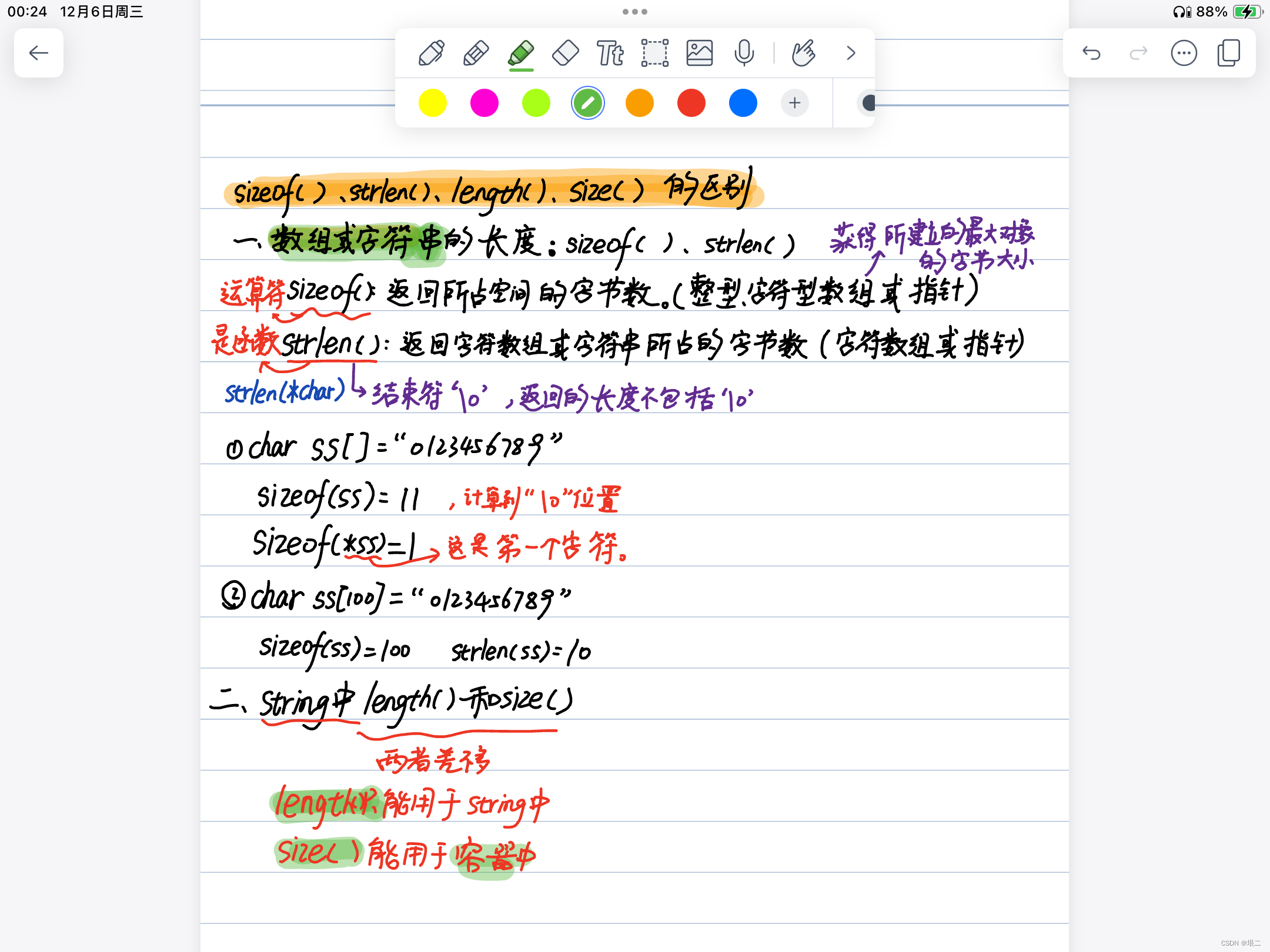
sizeof()、strlen()、length()、size()的区别(笔记)
上面的笔记有点简陋,可以看一下下面这个博主的: c/c中sizeof()、strlen()、length()、size()详解和区别_csize,sizeof,length_xuechanba的博客-CSDN博客...
)
Redis击穿(热点key失效)
Redis击穿是指在高并发情况下,一个键在缓存中过期失效时,同时有大量请求访问该键,导致所有请求都落到数据库上,对数据库造成压力。这种情况下,数据库可能无法及时处理这些请求,导致性能下降甚至崩溃。 为了…...

分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测
分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测 目录 分类预测 | Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现OOA-CNN-SVM鱼鹰算法优化卷积支持向量机分类预测࿰…...
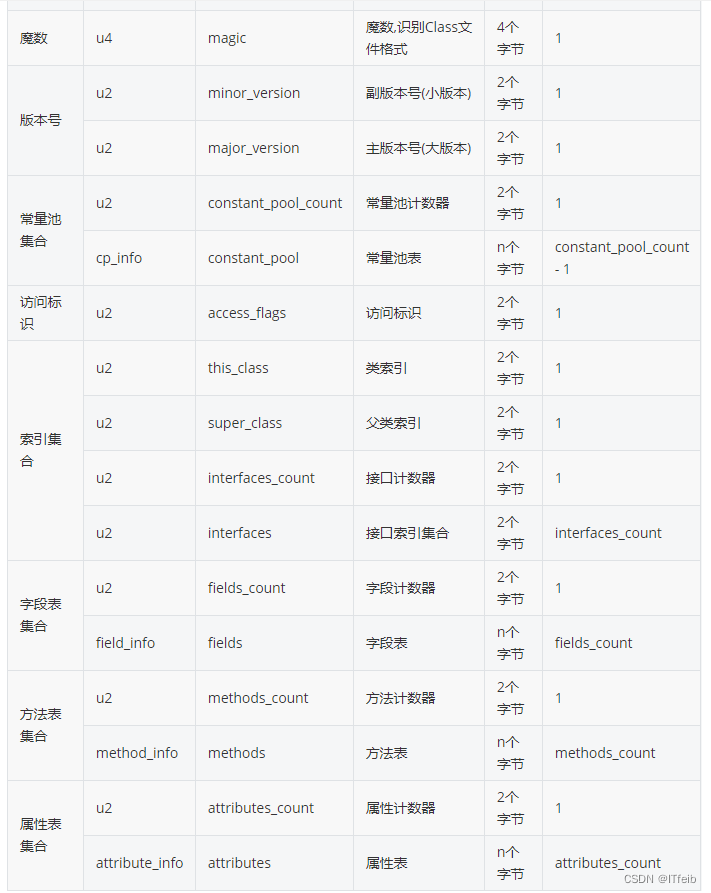
class文件结构
文章目录 1. 常量池集合2. 访问标志3. 字段表集合4. 方法表集合5. 属性表集合 成员变量(非静态)的赋值过程:1. 默认初始化 2. 显示初始化/代码块中初始化 3. 构造器中初始化 4. 有了对象后对象。属性或者对象。方法的方式对成员变量进行赋值 …...

多重背包问题 一句话说清楚“二进制拆分“
目录 区别: 一句话说清楚: 板子: 区别: 得先懂完全背包问题完全背包问题 非零基础-CSDN博客 都是让背包内价值最大。 完全背包问题每种物品可以取无数次。而多重背包问题每件取的次数有限。 都可以用的最挫的方法就是0~k件去…...

nodejs微信小程序+python+PHP本科生优秀作业交流网站的设计与实现-计算机毕业设计推荐
通过软件的需求分析已经获得了系统的基本功能需求,根据需求,将本科生优秀作业交流网站功能模块主要分为管理员模块。管理员添加系统首页、个人中心、用户管理、作业分类管理、作业分享管理、论坛交流、投诉举报、系统管理等操作。 随着信息化社会的形成…...

使用git出现的问题
保证 首先保证自己的git已经下载 其次保证自己的gitee账号已经安装并且已经生成ssh公钥 保证自己要push的代码在要上传的文件夹内并且配置文件等都在父文件夹(也就是文件没有套着文件) 问题 1 $ git push origin master gitgitee.com: Permission de…...
)
rk3568 适配PCIE(二)
rk3568 适配pcie3.0 PCIe(Peripheral Component Interconnect Express)是一种用于连接计算机主板和其他设备的高速串行总线接口。PCIe 2.0和PCIe 3.0是两个不同版本的PCIe规范,它们在以下几个方面有所不同: 带宽:PCIe 2.0的理论带宽为每条通道5 Gbps,而PCIe 3.0的理论带…...

Java基础 进制
在Java中,可以使用不同的进制表示整数常量和字面量。 十进制(Decimal):默认为十进制,不需要添加前缀。例如:int num 10;二进制(Binary):以0b或0B作为前缀表示二进制。例…...

springboot中@Builder注解的详细用法实例,跟数据库结合。
在Spring Boot中,Builder注解是Lombok库提供的一个注解,用于生成带有Builder模式支持的构造器方法。通过Builder注解,可以简化对象的创建过程,特别适用于需要设置多个属性的情况。 下面是一个使用Builder注解的示例: …...

WT2605C蓝牙音频语音芯片:具备大功率IO驱动能力,引领音频技术新纪元
在当今的电子科技时代,功率强大的IO驱动能力成为音频设备性能的重要指标。近日,一款名为WT2605C的蓝牙音频语音芯片,以其最高可直接驱动64mA的大功率IO驱动能力,引起业界的广泛关注。这款芯片的出现,无疑将为音频设备的…...

【Java 基础】20 多线程操作方法
文章目录 1.获取和设置线程的名字1)获取默认名字2)获取自定义的名字 2.判断线程是否启动3.线程的强制执行4.让线程睡一会儿5.中断线程6.守护线程7.线程的礼让 前一节我们介绍了线程的定义、创建方法、状态以及各状态间的转换。在状态转换处只是简单的说明…...

SpringBoot使用mybatis-plus分页查询无效解决方案
问题概述 SpringBoot中使用mybatis-plus实现分页查询时,提供一个page分页对象和一个QueryWrapper条件类对象,在使用Service.page(page,queryWrapper)方法进行分页查询时,发现并未查询到分页的结果,反而是查询到全部符合条件的结果…...
)
QT 中 线程池 (备查)
QRunnable类 API 1)在Qt中使用线程池需要先创建任务,添加到线程池中的每一个任务都需要是一个 QRunnable 类型,因此在程序中需要创建子类继承 QRunnable 这个类。 2)然后重写 run() 方法,在这个函数中编写要在线程池中…...

LeetCode刷题笔记第71题:简化路径
LeetCode刷题笔记第71题:简化路径 题目 给定一个路径,简化路径 要求: 1、以’/‘开头 2、两个目录之间只有一个’/’ 3、不能以’/‘结尾 4、路径中不能有’.‘和’…’ 想法 利用栈的数据存储方式的思想,将路径字符顺序入栈遇…...
JavaScript <md5加密的两种不同输出结果分析>--案例(二点一)
前言: 问题是这样的,在浏览器中看到这段代码 然后在控制台进行输出.得到: 紧接着,就在,js文件里面进行转译: 可是,得到的结果是: 这是问题!!! 正题: 为什么相同的js代码,在 .js 文件中的输出与 Chrome 控制台中的输出不一样? 环境差异:不同的JavaScript环境&…...
『亚马逊云科技产品测评』活动征文|基于亚马逊EC2云服务器配置Nginx静态网页
授权声明:本篇文章授权活动官方亚马逊云科技文章转发、改写权,包括不限于在 Developer Centre, 知乎,自媒体平台,第三方开发者媒体等亚马逊云科技官方渠道 亚马逊EC2云服务器(Elastic Compute Cloud)是亚马…...
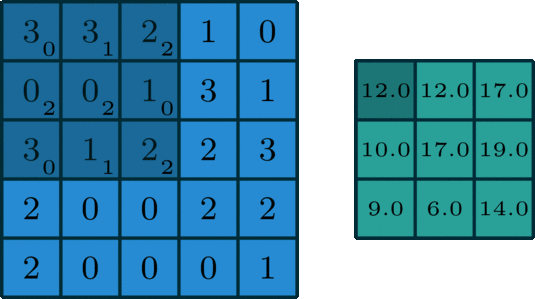
28、卷积 - 卷积的基础公式
本节推导一下卷积的基础公式,还是先上一张卷积运算的示意图图。 我们知道,一张图片有 3 个维度,分别是长、宽、通道。 这三个维度分别用 3 个字母代替,分别是 H(Height, 对应的是长这一维度), W(Width, 对应的是宽这一维度),C(Channel,对应的是通道这一维度)。 对于…...

Mac电脑vm虚拟机 VMware Fusion Pro中文 for mac
VMware Fusion Pro是一款功能强大的虚拟机软件,适用于需要在Mac电脑上运行其他操作系统的用户。它具有广泛的支持、快速稳定的特点以及多种高级功能,可以满足用户的各种需求和场景。 多操作系统支持:VMware Fusion Pro允许在Mac电脑上运行多…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
