当前位置： 首页 > news >正文

【链表Linked List】力扣-24 两两交换链表中的节点

news 2025/12/15 22:05:14

目录

题目描述

解题过程

题目描述

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

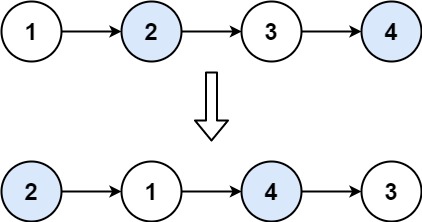
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

  • 链表中节点的数目在范围 [0, 100] 内
  • 0 <= Node.val <= 100

解题过程

 

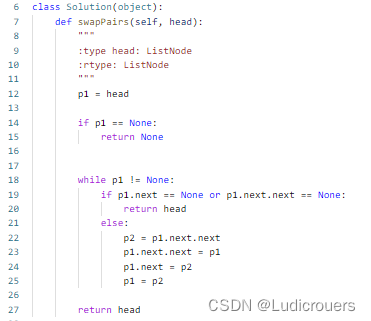
原以为很简单的一道题，还是出错了，错误如下：

错误原因： head指向没有考虑到，两个两个逆转后，组与组之间的连接没有考虑到，思考后做出如下更改：

 

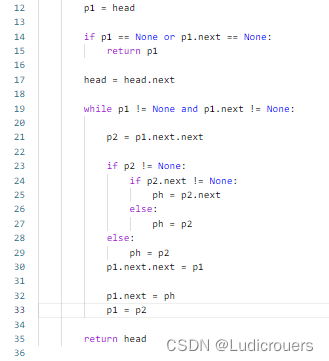
下次做题，要细心一点喽。 

相关文章：

【链表Linked List】力扣-24 两两交换链表中的节点

目录 题目描述 解题过程 题目描述 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0c;只能进行节点交换&#xff09;。 示例 1&#xff1a; 输入&#xff1a;he…...

编程日记 2023/12/6 9:41:26

企业微信协议开发，API接口调用

产品说明 一、 hook版本&#xff1a;企业微信hook接口是指将企业微信的功能封装成dll&#xff0c;并提供简易的接口给程序调用。通过hook技术&#xff0c;可以在不修改企业微信客户端源代码的情况下&#xff0c;实现对企业微信客户端的功能进行扩展和定制化。企业微信hook接口…...

编程日记 2023/12/6 9:40:24

代码随想录算法训练营 ---第五十五天

今天是 动态规划&#xff1a;编辑距离问题。 第一题&#xff1a; 简介&#xff1a; 动态规划五部曲&#xff1a; 1.确定dp数组的含义 dp[i][j] 表示以下标i-1为结尾的字符串s&#xff0c;和以下标j-1为结尾的字符串t&#xff0c;相同子序列的长度为dp[i][j]。 2.确定递推公…...

编程日记 2023/12/6 9:39:23

【Intel/Altera】 全系列FPGA最新汇总说明，持续更新中

前言 2023年11月14日英特尔 FPGA中国技术日&#xff0c;Intel刚发布了新的FPGA系列&#xff0c;官网信息太多&#xff0c;我这里结合以前的信息&#xff0c;简单汇总更新一下&#xff0c;方便大家快速了解Intel/Altera FPGA家族。 目录 前言 Altera和Intel 型号汇总 1. Agi…...

编程日记 2023/12/6 9:38:23

利用flask将yolov5算法封装成在线推理服务

本脚本主要参考了yolov5工程文件夹下面的detect.py，将yolov5算法封装成了一个在线的推理服务，可以接受app请求，然后推理图片，并将检测结果以json返回，该服务可以供数据标注平台请求。 from flask import * import shutil import json import os import pynvml import pand…...

编程日记 2023/12/6 9:37:22

vue3父子传值实现弹框功能

在Vue3中&#xff0c;我们可以通过 provide 和 inject 来实现父子组件之间的数据传递&#xff0c;这也适用于实现弹框功能。下面是一个简单的例子&#xff1a; 父组件代码&#xff1a; <template><div><button click"showDialog">打开弹框</b…...

编程日记 2023/12/6 9:36:21

C++入门【2-C++ 数据类型】

C 数据类型 使用编程语言进行编程时&#xff0c;需要用到各种变量来存储各种信息。变量保留的是它所存储的值的内存位置。这意味着&#xff0c;当您创建一个变量时&#xff0c;就会在内存中保留一些空间。 您可能需要存储各种数据类型&#xff08;比如字符型、宽字符型、整型…...

编程日记 2023/12/6 9:35:20

按照官网文档 通过useExtendedLib扩展库 引入WeUI，报错 组件未定义 | 解决办法

检查开发者工具版本是否过老 参考博客 不要使用 游客模式&#xff0c;游客模式不支持&#xff0c;请注册Appid 使用。 注意 扩展库方式 和 npm 方式不能同时使用&#xff0c;会有相应报错...

编程日记 2023/12/6 9:34:19

Chat-GPT原理

Chat-GPT原理核心:基于Transformer 架构 ​ 以下是参考文献的部分截图原文说明&#xff1a; ​ Transformers are based on the “attention mechanism,” which allows the model to pay more attention to some inputs than others, regardless of where they show up in t…...

编程日记 2023/12/6 9:33:18

GODOC命令无效，原因是需要手动安装

在看《GO程序设计语言》这本书&#xff0c;按照其中的内容&#xff0c;想看下GO自带的包的文档。 书中讲&#xff0c;可以直接输入GoDOC命令来打开一个服务器&#xff0c;从而可以用浏览器访问文档库。输入命令后&#xff0c;系统提示找不到该命令。 查了资料后才发现&#xff…...

编程日记 2023/12/6 9:30:16

忽略python运行出现的大量警告

添加以下代码即可 import warnings warnings.filterwarnings(ignore)...

编程日记 2023/12/6 9:25:12

【Polar靶场WEB签到】

题目&#xff1a; <?phperror_reporting(0);$file $_GET[file];if(!isset($file))$file 1;$file str_replace(../, , $file);include_once($file.".php");highlight_file(__FILE__); ?>解答&#xff1a;1、进入index页面&#xff0c;说让你加弟弟&#x…...

编程日记 2023/12/6 9:23:10

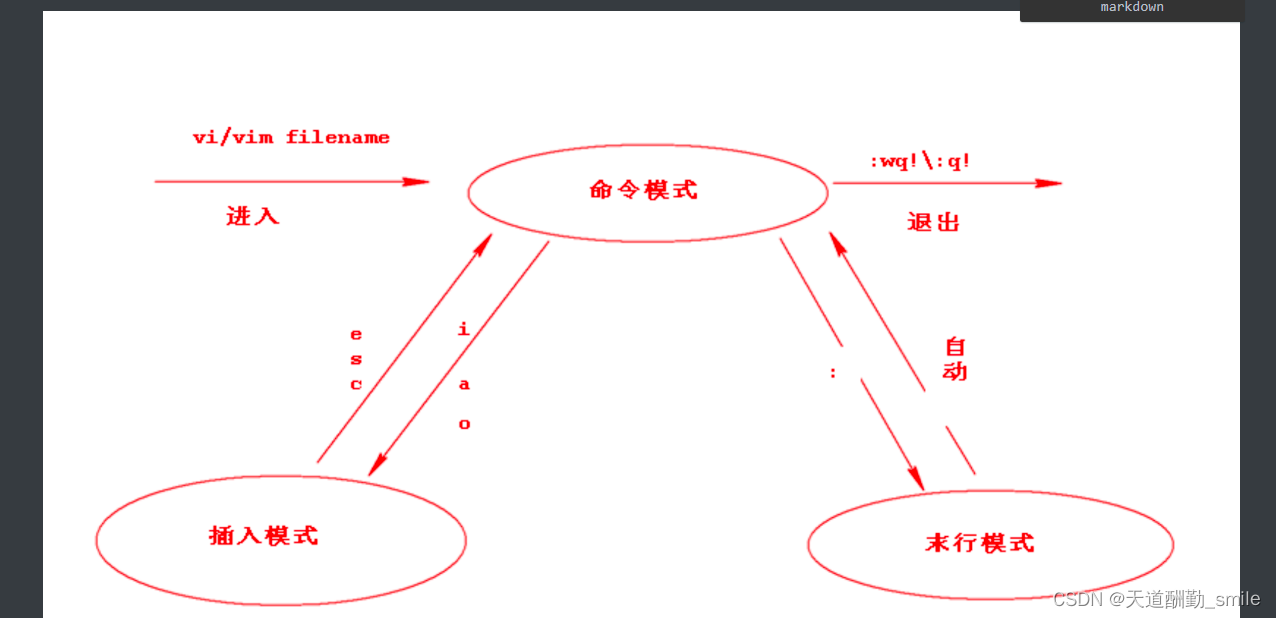
Linux详解——常用命令(二)

目录 一、常用命令 1.进程相关命令 2.vi命令 3.软件相关命令 RPM命令 YUM命令 4.用户和组相关命令 5.权限相关命令 一、常用命令 1.进程相关命令 # 1.ps 询在当前控制台上运行的进程 ps -aux 说明:查询系统中所有运行的进程&#xff0c;包括后台进程&#xff0c;其…...

编程日记 2023/12/6 9:15:04

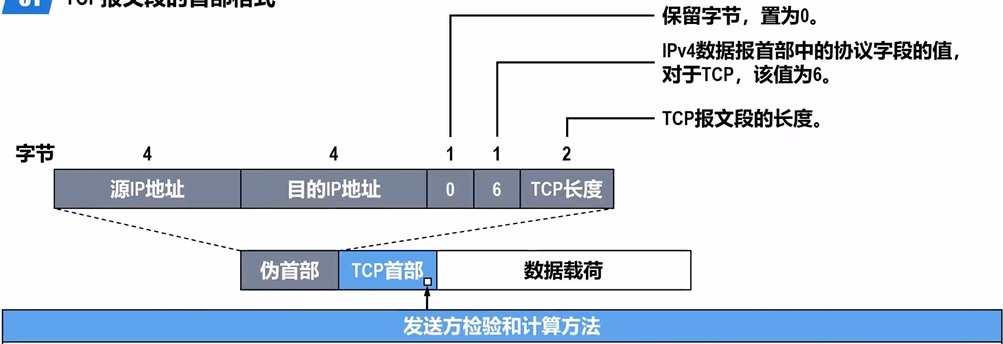
TCP首部格式_基本知识

TCP首部格式 表格索引: 源端口目的端口 序号 确认号 数据偏移保留 ACK等 窗口检验和紧急指针 TCP报文段首部格式图 源端口与目的端口: 各占16位 序号:占32比特&#xff0c;取值范围0~232-1。当序号增加到最后一个时&#xff0c;下一个序号又回到0。用来指出本TCP报文段数据载…...

编程日记 2023/12/6 9:13:03

MIT线性代数笔记-第23讲-微分方程，exp(At)

目录 23.微分方程&#xff0c; e x p ( A t ) exp(At) exp(At)用矩阵求解微分方程矩阵指数二阶常微分方程 打赏 23.微分方程&#xff0c; e x p ( A t ) exp(At) exp(At) 用矩阵求解微分方程 例&#xff1a; { d u 1 d t − u 1 2 u 2 d u 2 d t u 1 − 2 u 2 \left \{ \b…...

编程日记 2023/12/6 9:12:02

windows下安装配置kafka

一、安装zookeeper 在使用Kafka之前&#xff0c;通常需要先安装和配置ZooKeeper。ZooKeeper是Kafka的依赖项之一&#xff0c;它用于协调和管理Kafka集群的状态。 ZooKeeper是一个开源的分布式协调服务&#xff0c;它提供了可靠的数据存储和协调机制&#xff0c;用于协调分布式…...

编程日记 2023/12/6 9:10:00

TV遥控器模拟鼠标键

需求 &#xff1a; tv上部分app不支持光标选中&#xff0c;如亚马逊&#xff0c;插上鼠标不方便&#xff0c;即可以用遥控器模拟鼠标滚动和点击 1.拦截上下左右键 在WMS::PhoneWindowManager::interceptKeyBeforeQueueing中监听上下左右左右键&#xff0c;进行拦截。 Overrid…...

编程日记 2023/12/6 9:07:58

检测判断IP合法性API接口

检测判断IP合法性API接口 一、检测判断IP合法性API接口二、使用步骤1、接口2、请求参数3、请求参数示例4、接口 返回示例 三、 如何获取appKey和uid1、申请appKey:2、获取appKey和uid 四、重要说明 一、检测判断IP合法性API接口 一款免费的帮助你检测判断IP合法性API接口 二、…...

编程日记 2023/12/6 9:06:56

Linux swatch命令教程：如何监控系统活动(附案例详解和注意事项)

Linux swatch命令介绍 Swatch&#xff0c;全称为Simple Watcher&#xff0c;是一个简单的监视器&#xff0c;设计用于监控系统活动。为了使Swatch有用&#xff0c;它需要一个配置文件&#xff0c;该文件包含要查找的模式和在找到每个模式时要执行的操作。 Linux swatch命令适…...

编程日记 2023/12/6 9:05:55

加州大学伯克利分校研究人员推出Starling-7B：一款通过人工智能反馈强化学习（RLAIF）训练的开源大型语言模型（LLM）

每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗&#xff1f;订阅我们的简报&#xff0c;深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同&#xff0c;从行业内部的深度分析和实用指南中受益。不要错过这个机会&#xff0c;成为AI领…...

编程日记 2023/12/6 9:03:53

观成科技：隐蔽隧道工具Ligolo-ng加密流量分析

1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具&#xff0c;该工具基于TUN接口实现其功能&#xff0c;利用反向TCP/TLS连接建立一条隐蔽的通信信道&#xff0c;支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式&#xff0c;适应复杂网…...

编程新知 2025/12/14 9:57:46

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2025/8/4 18:55:37

在rocky linux 9.5上在线安装 docker

前面是指南&#xff0c;后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

编程新知 2025/7/27 10:03:12

python/java环境配置

环境变量放一起 python&#xff1a; 1.首先下载Python Python下载地址&#xff1a;Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个&#xff0c;然后自定义&#xff0c;全选 可以把前4个选上 3.环境配置 1&#xff09;搜高级系统设置 2…...

编程新知 2025/12/15 13:15:32

ssc377d修改flash分区大小

1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

编程新知 2025/8/4 2:45:15

java 实现excel文件转pdf | 无水印 | 无限制

文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具，自己手写的难度，恐怕高级程序员花费一年的事件，也…...

编程新知 2025/11/5 4:10:42

家政维修平台实战20：权限设计

目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系&#xff0c;主要是分成几个表&#xff0c;用户表我们是记录用户的基础信息&#xff0c;包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题&#xff0c;不同的角色&#xf…...

编程新知 2025/12/14 1:11:38

BCS 2025｜百度副总裁陈洋：智能体在安全领域的应用实践

6月5日&#xff0c;2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席&#xff0c;并作《智能体在安全领域的应用实践》主题演讲&#xff0c;分享了在智能体在安全领域的突破性实践。他指出&#xff0c;百度通过将安全能力…...

编程新知 2025/12/15 13:24:52

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/11/12 7:08:59

第 86 场周赛：矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词

Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵&#xff0c;其中每行&#xff0c;每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid&#xff0c;其中有多少个 3 3 的 “幻方” 子矩阵&am…...

编程新知 2025/12/13 5:55:42