数据结构 | 二叉树的各种遍历
数据结构 | 二叉树的各种遍历
文章目录
- 数据结构 | 二叉树的各种遍历
- 创建节点 && 创建树
- 二叉树的前中后序遍历
- 二叉树节点个数
- 二叉树叶子节点个数
- 二叉树第k层节点个数
- 二叉树查找值为x的节点
- 二叉树求树的高度
- 二叉树的层序遍历
- 判断二叉树是否是完全二叉树
我们本章来实现二叉树的这些功能
Tree.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;//创建节点
BTNode* BuyTreeNode(int x);
//创建树
BTNode* CreateTree();
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
// 求树的高度
int TreeHeight(BTNode* root);
- 我们先来几个简单的
创建节点 && 创建树
- 直接手动个创建即可,很简单~~
//创建节点
BTNode* BuyTreeNode(int x)
{BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail\n");exit(-1);}root->data = x;root->left = NULL;root->right = NULL;return root;
}
//创建树
BTNode* CreateTree()
{BTNode* node1 = BuyTreeNode(1);BTNode* node2 = BuyTreeNode(2);BTNode* node3 = BuyTreeNode(3);BTNode* node4 = BuyTreeNode(4);BTNode* node5 = BuyTreeNode(5);BTNode* node6 = BuyTreeNode(6);BTNode* node7 = BuyTreeNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node5->right = node7;return node1;
}
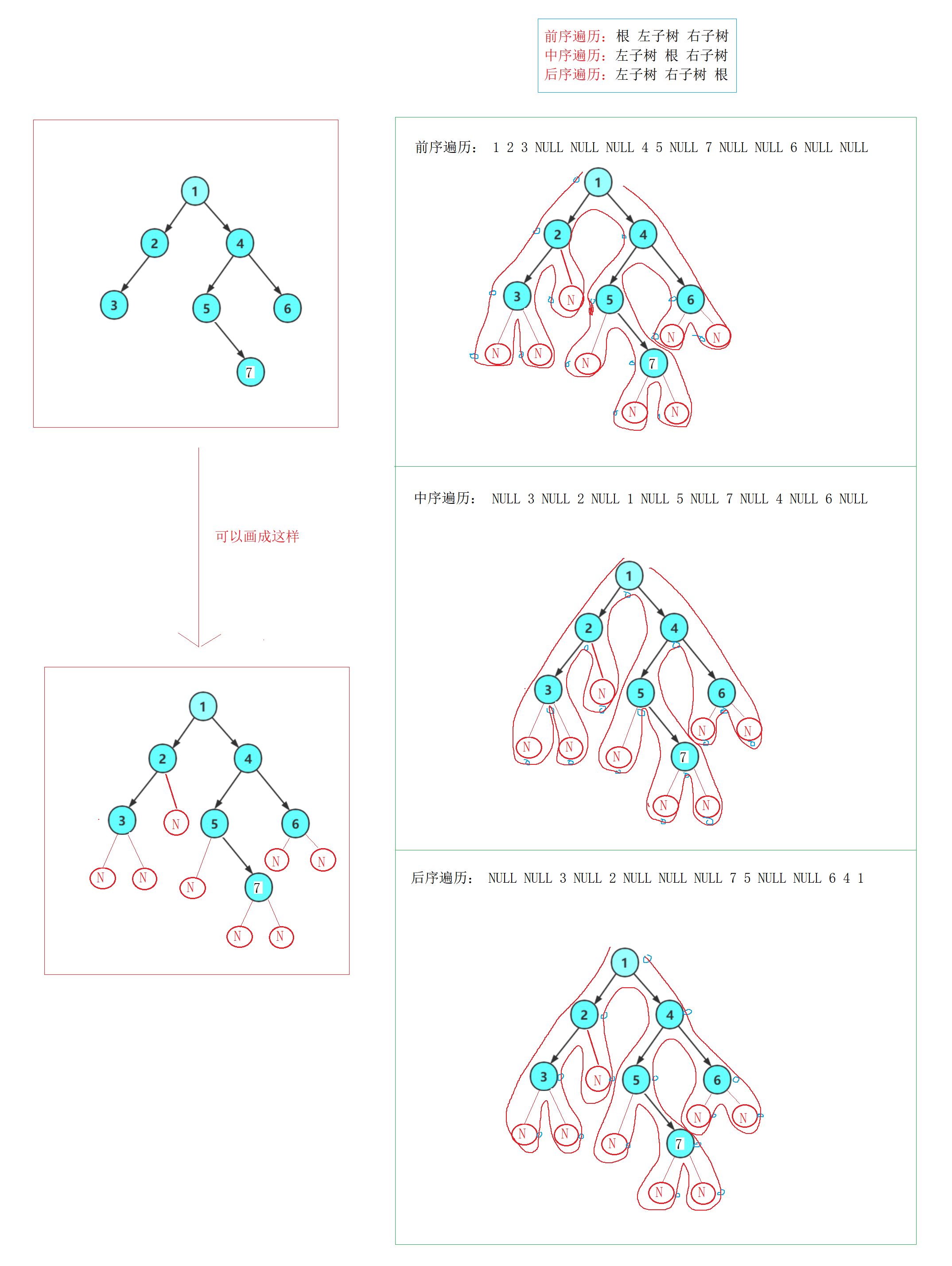
二叉树的前中后序遍历
- 这里也是很简单,也可以看做下图这样遍历,或者画一下递归展开图
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreeInOrder(root->left);printf("%d ", root->data);BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
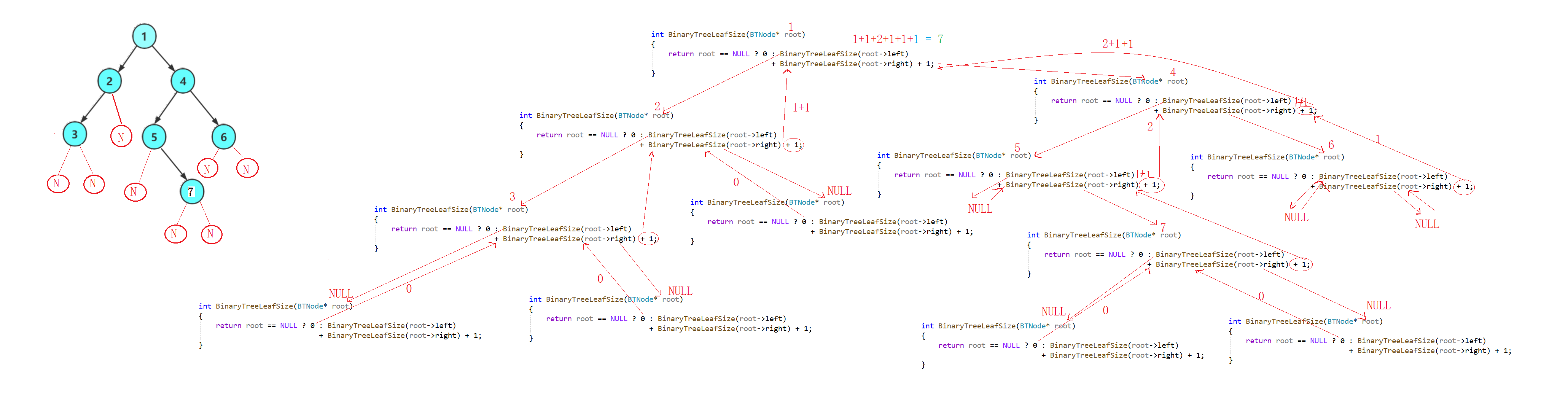
二叉树节点个数
- 我们这里看一下递归展开图
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->left)+ BinaryTreeSize(root->right);
}
二叉树叶子节点个数
- 为空就返回0
- 不是空,是叶子,返回1
- 不是空,也不是叶子,就递归左子树和右子树
int BinaryTreeLeafSize(BTNode* root)
{// 为空返回0if (root == NULL)return 0;//不是空,是叶子 返回1if (root->left == NULL && root->right == NULL)return 1;// 不是空 也不是叶子 分治=左右子树叶子之和return BinaryTreeLeafSize(root->left)+ BinaryTreeLeafSize(root->right);
}
二叉树第k层节点个数
- k是1的时候就是一层,就返回1
- 递归左子树加右子树,每次递归k-1
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL)return NULL;if (k == 1)return 1;//递归左子树加右子树,每次递归k-1return BinaryTreeLevelKSize(root->left, k - 1)+ BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
- 先看根节点是不是要找的
- 然后递归左子树和右子树
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;//根if (root->data == x)return root;//左子树BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;//右子树BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}
二叉树求树的高度
- 遍历左子树和右子树(每次遍历都要保存值)
- 返回最高的那个子树然后加1(根)
int TreeHeight(BTNode* root)
{if (root == NULL)return NULL;//遍历左子树和右子树int left = TreeHeight(root->left);int right = TreeHeight(root->right);//返回最高的那个子树然后加1(根)return left > right ? left + 1 : right + 1;
}
二叉树的层序遍历
- 这里的这个层序遍历就需要用到我们之前学过的队列了~~
- 这里用法是入根(root),然后带孩子节点
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);//打印数据printf("%d ", front->data);//将左子树和右子树代入进队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestroy(&q);
}
- 那如果要一层一层的打印,代码改怎么改呢?
- 一层一层的带,一层一层的出
// 层序遍历(一层一层的打印)
void _BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);int leveSize = 1;while (!QueueEmpty(&q)){while (leveSize--){//取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");leveSize = QueueSize(&q);}QueueDestroy(&q);
}
判断二叉树是否是完全二叉树
- 和上面的代码基本一样,取数据如果遇到空就跳出
- 如果前面遇到空以后,后面还有非空就不是完全二叉树
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);//先入根if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){// 取队头的数据BTNode* front = QueueFront(&q);QueuePop(&q);//等于空了就跳出,然后检查后面还有节点没有if (front == NULL)break;// 将左子树和右子树代入进队列QueuePush(&q, front->left);QueuePush(&q, front->right);}// 前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 如果是不是空就 return false;if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
相关文章:

数据结构 | 二叉树的各种遍历
数据结构 | 二叉树的各种遍历 文章目录 数据结构 | 二叉树的各种遍历创建节点 && 创建树二叉树的前中后序遍历二叉树节点个数二叉树叶子节点个数二叉树第k层节点个数二叉树查找值为x的节点二叉树求树的高度二叉树的层序遍历判断二叉树是否是完全二叉树 我们本章来实现二…...

Python-赋值运算符(详解)
表示赋值 左侧为变量,右边为值 a b 10#先把10赋值给b,再把b赋值给a 相当于a 10 b 10 链式赋值,但是不推荐,一般一行一个语句,提高可读性,良好的代码风格 多元赋值: a , b 10,20 #python语…...

算法工程师面试八股(搜广推方向)
文章目录 机器学习线性和逻辑回归模型逻辑回归二分类和多分类的损失函数二分类为什么用交叉熵损失而不用MSE损失?偏差与方差Layer Normalization 和 Batch NormalizationSVM数据不均衡特征选择排序模型树模型进行特征工程的原因GBDTLR和GBDTRF和GBDTXGBoost二阶泰勒…...
)
学习TypeScrip4(数组类型)
数组的类型 1.定义方法:类型[ ] //类型加中括号 let arr:number[] [123] //这样会报错定义了数字类型出现字符串是不允许的 let arr:number[] [1,2,3,1] //操作方法添加也是不允许的 let arr:number[] [1,2,3,] arr.unshift(1)var arr: number[] [1, 2, 3]; /…...
Python文件打包成exe可执行文件
我们平常用python写些脚本可以方便我们的学习办公,但限制就是需要有python环境才能运行。 那能不能直接在没有python环境的电脑上运行我们的脚本呢? 当然可以,那就是直接把python脚本打包成exe可执行程序(注针对win系统…...
Android : SQLite 增删改查—简单应用
示例图: 学生实体类 Student.java package com.example.mysqlite.dto;public class Student {public Long id;public String name;public String sex;public int age;public String clazz;public String creatDate;//头像public byte[] logoHead;Overridepublic St…...

【蓝桥杯】马的遍历
马的遍历 题目描述 有一个 n m n \times m nm 的棋盘,在某个点 ( x , y ) (x, y) (x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。 输入格式 输入只有一行四个整数,分别为 n , m , x , y n, m, x, y n,m,x,y。 …...

导入JSON到xmind
写在前面 这只是一个思路,解决大量树状数据,创建xmind低效问题。 函数可以根据你的实际情况优化 1. 转换json格式 function formatToXimd(atd, str) {if (atd) {for (let index 0; index < atd.length; index) {console.log(str - atd[index].…...
DataGrip 2023.2.3(IDE数据库开发)
DataGrip是一款数据库集成开发环境(IDE),用于数据库管理和开发。 DataGrip提供了许多强大的功能,如SQL语句编辑、数据库连接管理、数据导入和导出、数据库比较和同步等等。它支持多种数据库,如MySQL、PostgreSQL、Ora…...

身为 Go 程序员,我为啥更喜欢用 Zig?
Zig 是一种比较新的编程语言,于 2016 年首次推出。Zig 社区将其描述为“一种用于维护稳固的、可优化和可重用软件的通用编程语言”。 看似一句简单的描述,却隐藏着远大的抱负。Zig被看作是可与C语言一较高下的编程语言。此外,Zig 也是一个编…...
Amazon CodeWhisperer 使用体验
文章作者:STRIVE Amazon CodeWhisperer 是最新的代码生成工具,支持多种编程语言,如 java,js,Python 等,能减少开发人员手敲代码时间,提升工作效率。PS:本人是一名 CodeWhisperer 业余爱好者 亚马逊云科技开发者社区为开…...
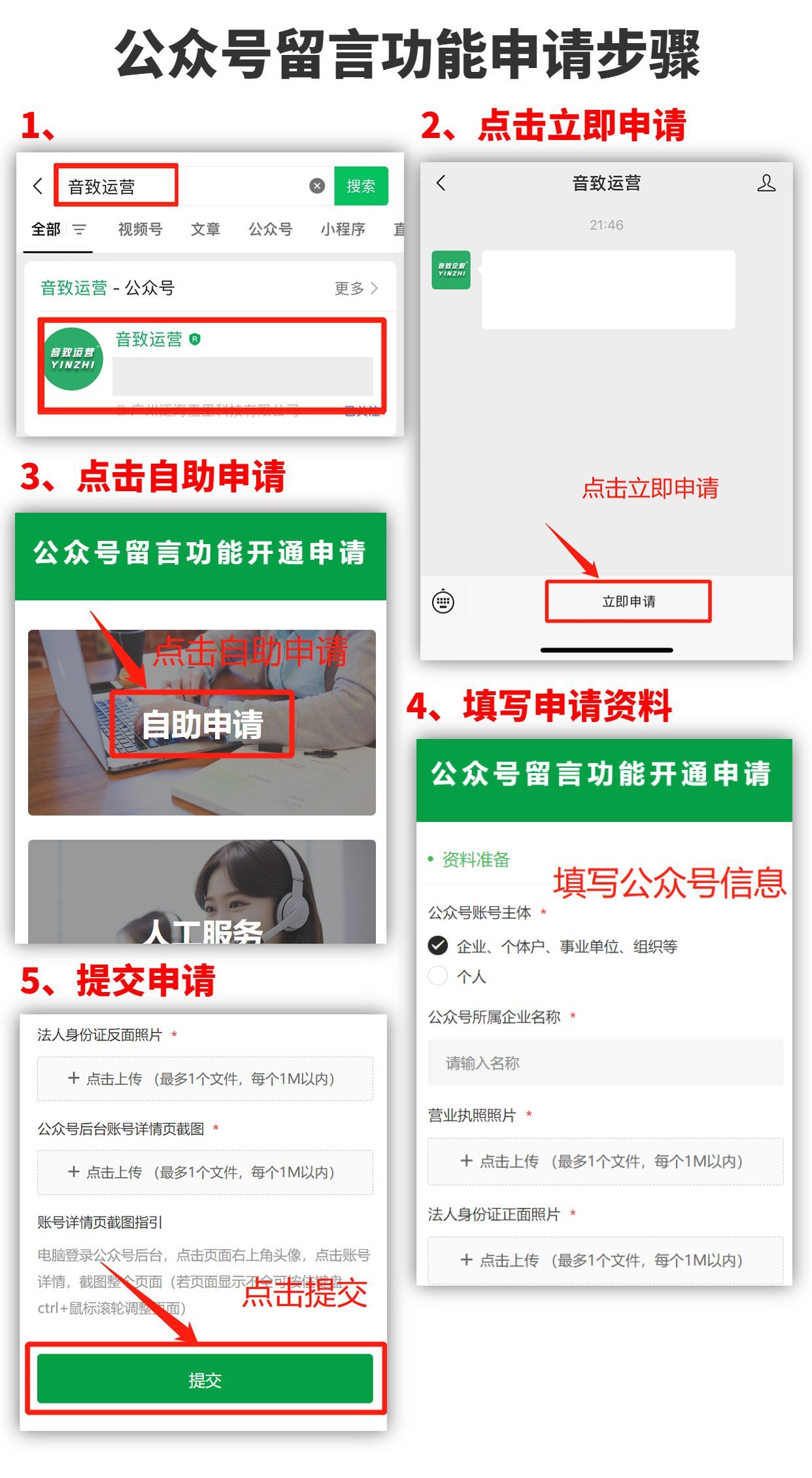
公众号留言功能怎么申请?
为什么公众号没有留言功能?2018年2月12日,TX新规出台:根据相关规定和平台规则要求,我们暂时调整留言功能开放规则,后续新注册帐号无留言功能。这就意味着2018年2月12日号之后注册的公众号不论个人主体还是组织主体&…...
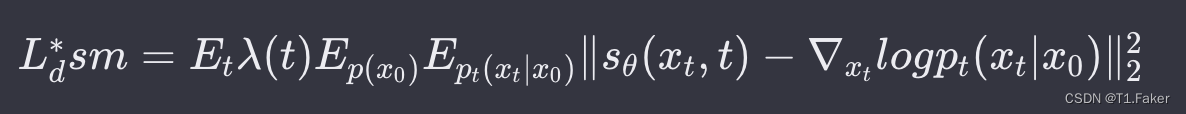
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion
探索三种生成模型:基于DDPMs、NCSNs和SDEs方法的Diffusion 去噪扩散概率模型(DDPMs)正向过程反向过程 噪声条件得分网络(NCSNs)正向过程初始化训练 NCSNs生成样本 反向过程 随机微分方程(SDEs)原…...
)
Linux随记(七)
一、欧拉bclinux 21.10安装zabbix-5.0.37.tar.gz (zbx-客户端) #系统环境: BigCloud Enterprise Linux For Euler 21.10 LTS #软件信息: zabbix-5.0.37.tar.gz , pcre-devel-8.44-2.oe1.x86_64.rpm , inst…...

RESTful API,以及如何使用它构建 web 应用程序。
RESTful API是一种基于REST(Representational State Transfer)架构风格的API(Application Programming Interface),它采用HTTP协议中的GET、POST、PUT、DELETE等方法,对资源进行操作。RESTful API的核心思想…...
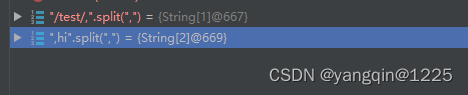
【华为OD题库-075】拼接URL-Java
题目 题目描述: 给定一个url前缀和url后缀,通过,分割。需要将其连接为一个完整的url。 如果前缀结尾和后缀开头都没有/,需要自动补上/连接符 如果前缀结尾和后缀开头都为/,需要自动去重 约束:不用考虑前后缀URL不合法情况 输入描述: url前缀(一个长度小于…...
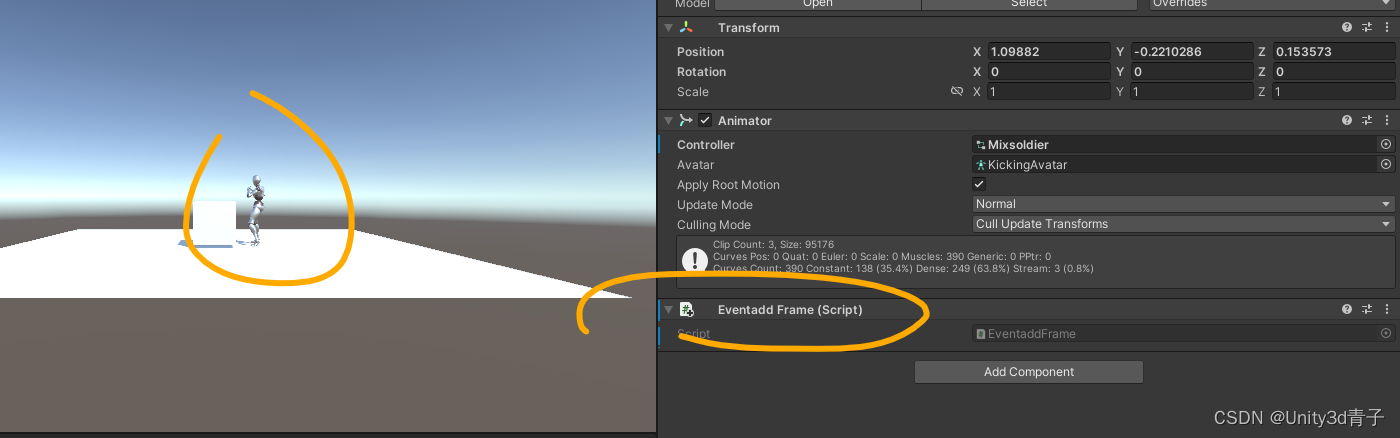
【Unity动画】为一个动画片段添加事件Events
动画不管播放到那一帧,我们都可以在这里“埋伏”一个事件(调用一个函数并且给函数传递一个参数,参数在外部设置,甚至传递一个物体)! 嗨,亲爱的Unity小伙伴们!你是否曾想过为你的动画…...
CoDeF视频处理——视频风格转化部署使用与源码解析
一、算法简介与功能 CoDef是作为一种新型的视频表示形式,它包括一个规范内容场,聚合整个视频中的静态内容,以及一个时间变形场,记录了从规范图像(即从规范内容场渲染而成)到每个单独帧的变换过程。针对目标…...

ubuntu server 20.04 备份和恢复 系统 LTS
ubuntu server 20.04 备份和恢复 系统 LTS tar命令系统备份与恢复(还原or新装) 备份系统 cd / su root tar cvpzf backup.tgz --exclude/tmp --exclude/run --exclude/dev --exclude/snap --exclude/proc --exclude/lostfound --exclude/backup.tgz …...

NFC对物联网开发的影响及用途
当谈到NFC对物联网的影响时,不得不提它的几个重要的优势,可能在未来几年影响着物联网的发展方向。 全球智能手机的普及是其中一个重要因素:市面上已有数十亿部支持NFC的智能手机,专家们相信这个数字还会大幅增长。智能手机用户已…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
