变分推断 (Variational Inference) 解析
前言
如果你对这篇文章可感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。
变分推断
在贝叶斯方法中,针对含有隐变量的学习和推理,通常有两类方式,其一是马尔可夫链蒙特卡罗法 (MCMC),其通过采样来近似估计后验概率分布;其二是变分推断,通过解析的方法近似计算后验概率分布。
假设联合概率分布 p(x,z)p(x,z)p(x,z),其中 xxx 是观测变量,即数据,zzz 是隐变量,目标是学习后验概率分布 p(z∣x)p(z\mid x)p(z∣x)。
由于 p(z∣x)p(z\mid x)p(z∣x) 通常非常复杂,难以直接求解,因此变分推断使用分布 q(z)q(z)q(z) 来近似 p(z∣x)p(z\mid x)p(z∣x),并通过限制 q(z)q(z)q(z) 形式,得到一种局部最优、但具有确定解的近似后验分布。其中 q(z)q(z)q(z) 即为变分分布 (variational distribution),q(z)q(z)q(z) 与 p(z∣x)p(z\mid x)p(z∣x) 之间的相似度通过 KL\text{KL}KL 散度衡量。
如下图所示,我们希望在集合 Q\mathcal{Q}Q 中找到 q∗(z)q^*(z)q∗(z) 使其与 p(z∣x)p(z\mid x)p(z∣x) 之间的 KL\text{KL}KL 散度尽可能小。
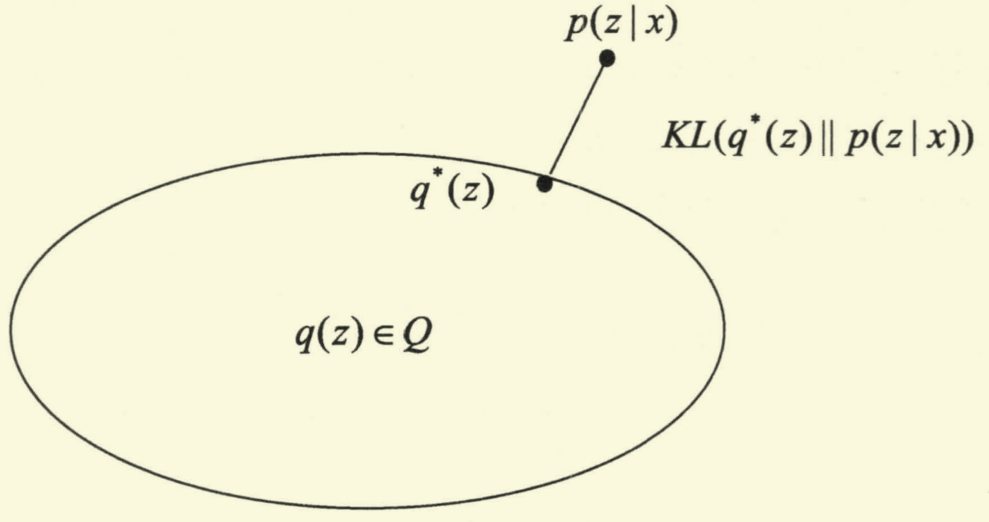
基于上述想法,对 KL(q(z)∥p(z∣x))\text{KL}(q(z)\|p(z\mid x))KL(q(z)∥p(z∣x)) 进行拆解:
KL(q(z)∥p(z∣x))=∫q(z)logq(z)dz−∫q(z)logp(z∣x)dz=logp(x)−{∫q(z)logp(x,z)dz−∫q(z)logq(z)dz}=logp(x)−Eq[logp(x,z)−logq(z)].\begin{aligned} \text{KL}(q(z)\| p(z\mid x)) &= \int q(z) \log q(z) \text{d} z - \int q(z) \log p(z\mid x) \text{d} z \\ &= \log p(x) - \left\{\int q(z) \log p(x,z) \text{d} z - \int q(z) \log q(z) \text{d} z\right\} \\ &= \log p(x) - \mathbb{E}_q\left[\log p(x,z)-\log q(z)\right]. \end{aligned} KL(q(z)∥p(z∣x))=∫q(z)logq(z)dz−∫q(z)logp(z∣x)dz=logp(x)−{∫q(z)logp(x,z)dz−∫q(z)logq(z)dz}=logp(x)−Eq[logp(x,z)−logq(z)].
由于 KL\text{KL}KL 散度非负,因此:
logp(x)≥Eq[logp(x,z)−logq(z)].\log p(x) \geq \mathbb{E}_q\left[\log p(x,z)-\log q(z)\right]. logp(x)≥Eq[logp(x,z)−logq(z)].
不等式左端为证据 (Evidence),右端则为证据下界 (Evidence Lower Bound, ELBO\text{ELBO}ELBO),记作 L(q)L(q)L(q)(ELBO 经常出现于各类与贝叶斯有关的文章中)。
我们的目的是求解 q(z)q(z)q(z) 来最小化 KL(q(z)∥p(z∣x))\text{KL}(q(z)\| p(z\mid x))KL(q(z)∥p(z∣x)),由于 logp(x)\log p(x)logp(x) 是常量,问题转化为最大化 ELBO\text{ELBO}ELBO L(q)L(q)L(q).
若 q(z)q(z)q(z) 形式过于复杂,最大化 ELBO\text{ELBO}ELBO 依然难以求解,因此通常会对 q(z)q(z)q(z) 形式进行约束,一种常见的方式是假设 zzz 服从分布
q(z)=∏iqi(zi),q(z)=\prod_{i} q_i(z_i), q(z)=i∏qi(zi),
即 zzz 可拆解为一系列相互独立的 ziz_izi,此时的变分分布称为平均场 (Mean Filed).
总结一下,变分推断常见步骤如下:
- 定义变分分布 q(z)q(z)q(z);
- 推导证据下界 ELBO\text{ELBO}ELBO 表达式;
- 最大化 ELBO\text{ELBO}ELBO,得到 q∗(z)q^*(z)q∗(z),作为后验概率分布 p(z∣x)p(z\mid x)p(z∣x) 的近似。
广义 EM
上述变分推断过程可以与「广义 EM」联系起来,由于 logp(x)≥ELBO\log p(x)\geq \text{ELBO}logp(x)≥ELBO 恒成立,若将模型参数 θ\thetaθ 引入其中,即可得到:
logp(x∣θ)≥Eq[logp(x,z∣θ)−logq(z)],\log p(x\mid \theta) \geq \mathbb{E}_q\left[\log p(x,z\mid \theta)-\log q(z)\right], logp(x∣θ)≥Eq[logp(x,z∣θ)−logq(z)],
此时有两种理解:
- 用分布 q(z)q(z)q(z) 近似联合概率分布 p(x,z∣θ)p(x,z\mid \theta)p(x,z∣θ),最小化分布距离 KL(q∥p)\text{KL}(q\|p)KL(q∥p);
- 采用极大似然估计的思想,最大化对数似然函数 logp(x∣θ)\log p(x\mid \theta)logp(x∣θ)(也可以理解为最大化证据)。
虽然两种视角不同,但结论一致,即最大化 ELBO\text{ELBO}ELBO,记作 L(q,θ)L(q,\theta)L(q,θ)。对应于广义 EM 算法,即采用迭代的方式,循环执行 E 步和 M 步,直至收敛:
- 【E 步】固定 θ\thetaθ,求 L(q,θ)L(q,\theta)L(q,θ) 对 qqq 的最大化;
- 【M 步】固定 qqq,求 L(q,θ)L(q,\theta)L(q,θ) 对 θ\thetaθ 的最大化。
上述迭代可以保证 logp(x∣θ(t))\log p(x\mid \theta^{(t)})logp(x∣θ(t)) 不降,即一定会收敛,但可能会收敛到局部最优:
logp(x∣θ(t−1))=L(q(t),θ(t−1))≤L(q(t),θ(t))≤logp(x∣θ(t))\log p(x \mid \theta^{(t-1)})=L(q^{(t)}, \theta^{(t-1)}) \leq L(q^{(t)}, \theta^{(t)}) \leq \log p(x \mid \theta^{(t)}) logp(x∣θ(t−1))=L(q(t),θ(t−1))≤L(q(t),θ(t))≤logp(x∣θ(t))
其中「左边第一个等号」由变分推断原理 + E 步得到,「左边第一个不等号」由 M 步得到,「左边第二个不等号」由变分推断原理得到。
参考资料
- 周志华. (2016). 机器学习. 清华大学出版社, 北京.
- 李航. (2019). 统计学习方法. 清华大学出版社, 第 2 版, 北京.
相关文章:

变分推断 (Variational Inference) 解析
前言 如果你对这篇文章可感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。 变分推断 在贝叶斯方法中,针对含有隐变量的学习和推理,通常有两类方式,其一是马尔可…...

27. 移除元素
题目链接:https://leetcode.cn/problems/remove-element/给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输…...

hive临时目录清理
hive运行失败会导致临时目录无法自动清理,因此需要自己写脚本去进行清理 实际发现hive临时目录有两个: /tmp/hive/{user}/* /warehouse/tablespace//hive/**/.hive-staging_hive 分别由配置hive.exec.scratchdir和hive.exec.stagingdir决定: 要注意的…...

如何创建发布新品上市新闻稿
推出新产品对任何企业来说都是一个激动人心的时刻,但向潜在客户宣传并围绕您的新产品引起轰动也可能是一个挑战。最有效的方法之一就是通过发布新品上市新闻稿。精心制作的新闻稿可以帮助我们通过媒体报道、吸引并在目标受众中引起关注。下面,我们将讲述…...

关于.bashrc和setup.bash的理解
在创建了ROS的workspace后,需要将workspace中的setup.bash文件写入~/.bashrc 文件中,让其启动: source /opt/ros/melodic/setup.bash这句话的目的就是在开新的terminal的时候,运行这个setup.bash,而这个setup.bash的作…...
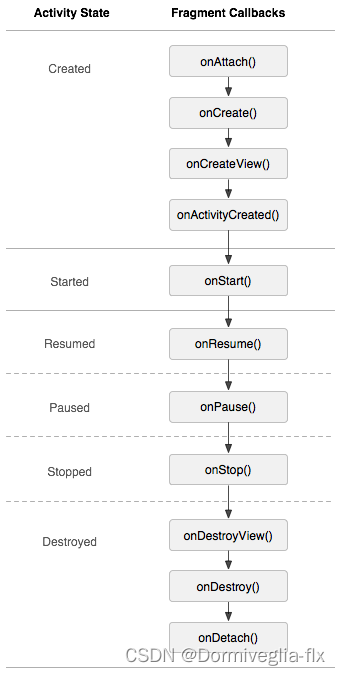
03 Android基础--fragment
03 Android基础--fragment什么是fragment?fragment生命周期?动态的fragment与静态的fragmentfragment常用的两个类与APIFragment与Activity通信什么是fragment? 碎片,一个activity中可以使用多个fragment,可以把activi…...
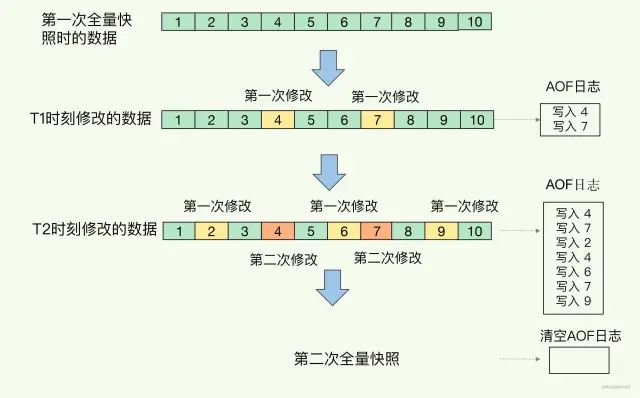
Redis使用,AOF、RDB
前言 如果有人问你:"你会把 Redis 用在什么业务场景下?" 我想你大概率会说:"我会把它当作缓存使用,因为它把后端数据库中的数据存储在内存中,然后直接从内存中读取数据,响应速度会非常快。…...
SOLIDWORKS Premium 2023 SP1.0 三维设计绘图软件
SOLIDWORKS 中文完美正式版提供广泛工具来处理最复杂的问题,并提供深层技术完成关键细节工作。新功能可助您改善产品开发流程,以更快地将创新产品投入生产。Solidworks 是达索公司最新推出的三维CAD系统,它可让设计师大大缩短产品的设计时间,让产品得以快速、高效地投向市场…...

PyQGIS开发--自动化地图布局案例
前言创建地图布局是 GIS 作业结束时的一项常见任务。 它用于呈现最终结果的输出,作为与用户交流的一种方式,以便从地图中获取信息、知识或见解。 在包括 QGIS 在内的任何 GIS 软件中制作地图布局都非常容易。 但另一方面,当我们必须生成如此大…...

严格模式和非严格模式下的this指向问题
一、全局环境 1.函数调用 非严格模式:this指向是Window // 普通函数 function fn () { console.log(this, this); } fn() // 自执行函数 (function fn () { console.log(this, this); })() 严格模式:this指向是undefined //…...

vue2、vue3组件传值,引用类型,对象数组如何处理
vue2、vue3组件传值,引用类型,对象数组如何处理 Excerpt 所有的 prop 都使得其父子 prop 之间形成了一个单向下行绑定:父级 prop 的更新会向下流动到子组件中,但是反过来则不行。这样会防止从子组件意外变更父… 下述组件传值指引…...

165. 小猫爬山
Powered by:NEFU AB-IN Link 文章目录165. 小猫爬山题意思路代码165. 小猫爬山 题意 翰翰和达达饲养了 N只小猫,这天,小猫们要去爬山。 经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了(呜咕…...

ECharts教程(详细)
ECharts教程(详细) 非常全面的ECharts教程,非常全面的ECharts教程,目前线条/节点颜色、线条粗细、线条样式、线条阴影、线条平滑、线条节点大小、线条节点阴影、线条节点边框、线条节点边框阴影、工具提醒、工具提醒样式、工具自定义提醒、工具提醒背景…...

pinia
目录一、介绍二、快速上手1.安装2.基本使用与state3.actions的使用4.getters的使用5.storeToRefs的使用6.pinia模块化三、数据持久化1.安装2.使用插件3.模块开启持久化4.按需缓存模块的数据一、介绍 pinia从使用角度和之前Vuex几乎是一样的,比Vuex更简单了。 在Vu…...

mysql中insert语句的五种用法
文章目录前言一、values参数后单行插入二、values参数后多行插入三、搭配select插入数据四、复制旧表的信息到新表五、搭配set插入数据总结前言 insert语句是标准sql中的语法,是插入数据的意思。在实际应用中,它也演变了很多种用法来实现特殊的功能&…...

YOLOV7模型调试记录
先前的YOLOv7模型是pytorch重构的,并非官方提供的源码,而在博主使用自己的数据集进行实验时发现效果并不理想,因此生怕是由于源码重构导致该问题,此外还需进行对比实验,因此便从官网上下载了源码,进行调试运…...
)
模拟光伏不确定性——拉丁超立方抽样生成及缩减场景(Matlab全代码)
光伏出力的不确定性主要源于预测误差,而研究表明预测误差(e)服从正态分布且大概为预测出力的10%。本代码采用拉丁超立方抽样实现场景生成[1,2]、基于概率距离的快速前代消除法实现场景缩减[3],以此模拟了光伏出力的不确定性。与风电不确定性模拟不同之处在于——光伏存在0出…...

Elasticsearch聚合查询速览
Es 数据分析工具 - Elasticsearch Aggregations (聚合查询) 官方文档 Aggregations | Elasticsearch Guide [7.15] | Elastic 1. Bucket aggregations 桶聚合 that group documents into buckets, also called bins, based on field values, ranges, o…...

CEC2017:鱼鹰优化算法(Osprey optimization algorithm,OOA)求解cec2017(提供MATLAB代码)
一、鱼鹰优化算法简介 鱼鹰优化算法(Osprey optimization algorithm,OOA)由Mohammad Dehghani 和 Pavel Trojovsk于2023年提出,其模拟鱼鹰的捕食行为。 鱼鹰是鹰形目、鹗科、鹗属的仅有的一种中型猛禽。雌雄相似。体长51-64厘米…...
Vue3 企业级项目实战:通关 Vue3 企业级项目开发,升职加薪快人一步
Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.juejin.cn/ds/S2RkR9F/ 课程介绍 很高兴为大家介绍这个…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
