R语言gWQS包在加权分位数和回归模型的应用
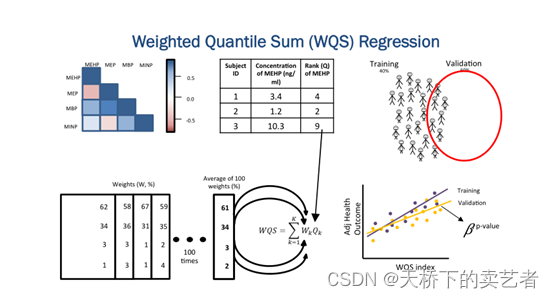
在流行病学研究中,相较于单一因素的暴露,多因素同时暴露的情况更为常见。传统模型在评价多因素联合暴露时存在数据维度高、多重共线性等问题. WQS 回归模型的基本原理是通过分位数间距及加权的方法,将多种研究因素的效应综合成为一个指数,再进行回归分析。不同因素赋予的权重反映了其对结局的影响程度。使用该模型时应满足各研究因素
对结局影响的方向相同这一基本假设.
模型的一般形式为:
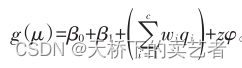
式中:c 表示污染物种类;β 0 表示截距;β 1 表示回归系数,用于限制联合效应对结局影响的方向;w i 表示第 i 种因素的未知权重,取值范围[0,1],且 ∑wi = 1,q i 表示对因素 i 进行 q 分位(如三、四分位等);

上公式表示c 种研究因素的综合权重指数;z 为协变量矩阵,φ为该矩阵的回归系数;g ( )为连接函数,μ 为均数。

下面咱们来进行演示一下,先导入R包和数据,数据使用的是gWQS自带的数据
library(gWQS)
library(ggplot2)
library(reshape2)
data(wqs_data)
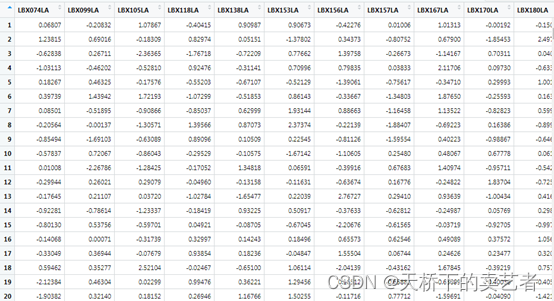
数据挺大的,上图只是数据的一部分,这些数据反映了参与NHANES研究(2001-2002)的受试者中34种多氯联苯暴露和25种邻苯二甲酸酯生物标志物的分布模拟的59种暴露浓度,概括来说就是一些指标的浓度,结局有连续变量和分类变量,还有性别作为协变量。
WQS 回归模型的思想就是把指标打包成一个指数,第一步先要确定咱们研究哪些指标,假设咱们研究的是前面34种指标
PCBs <- names(wqs_data)[1:34]
PCBs

然后就可以生成模型了, 通过 y ~ wqs+sex 将 y 与 34种 PCBs 的联合效应,建立回归方程并调整性别(sex)。其中wqs 是固定参数(即:必须包含项), mix_name=mix 表示指定联合暴露污染物,data =wqs_data 表示输入的数据集为 wqs_data;q=10表示将联合效应进行10分位,在实际运用过程中研究者可设置不同的分位数;validation=0.6 表示随机抽取数据集中的 60% 作为验证集,余下的 40% 作为训练集;b表示 bootstrap 随机抽样次数,该参数至少为 100;b1_pos=TRUE 表示设定联合效应的权重为正 (若为
负则设置为 FALSE);b1_constr=FALSE 表示使用优化算法对权重进行估计时不进行限制(若进行限制则设置为 TURE);family="gaussian"表示采用高斯分布进行拟合,也可根据研究对象的数据类型采用二项分布、多项式或泊松分布等进行拟合;由于涉及 boot⁃strap 随机抽样过程,将随机种子数 (seed) 设置为2021。
results2i <-gwqs (y ~ wqs+sex, mix_name=PCBs, data=wqs_data,q=10, validation=0.6, b=100, b1_pos=TRUE,b1_constr=FALSE, family="gaussian", seed=2021)
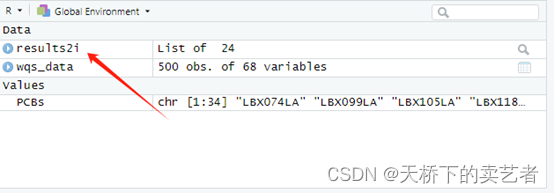
解析结果,可以看到这个联合指数是和结局相关的
summary(results2i)
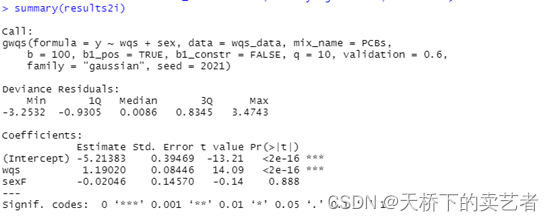
也可以使用gwqs解析函数,生成标准化表格
gwqs_summary_tab(results2i)
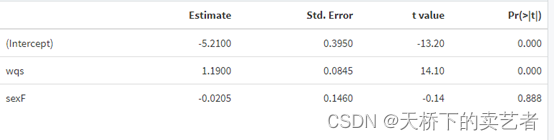
这样也可以查看系数和可信区间
summary(results2i)[["coefficients"]]
confint(results2i)
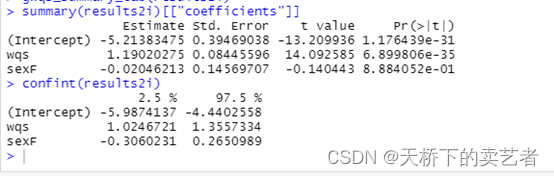
接下来咱们
咱们查看污染物权重构成比
gwqs_weights_tab(results2i)
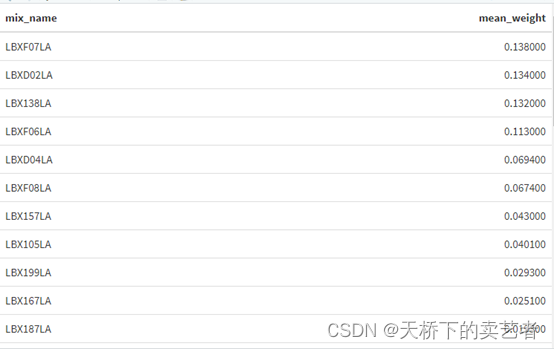
这样也可以的
results2i$final_weights
可以进一步可视化,画个条形图,咱们可以看到,前4个指标对结局影响最大
gwqs_barplot(results2i)
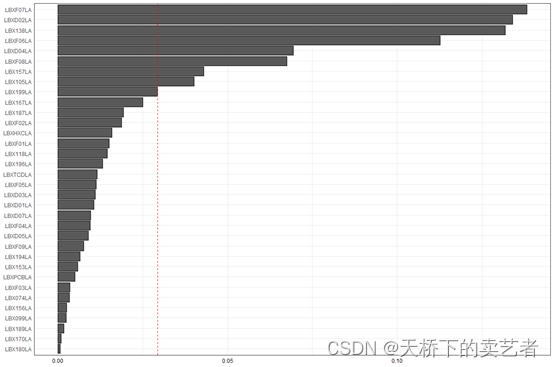
咱们也可以把数据提取出来使用ggplot来话,这样更加美观
w_ord <- order(results2i$final_weights$mean_weight)
mean_weight <- results2i$final_weights$mean_weight[w_ord]mix_name <- factor(results2i$final_weights$mix_name[w_ord],levels = results2i$final_weights$mix_name[w_ord])
dataplot <- data.frame(mean_weight, mix_name)ggplot(dataplot, aes(x = mix_name, y = mean_weight, fill = mix_name)) +geom_bar(stat = "identity", color = "black") + theme_bw() +theme(axis.ticks = element_blank(),axis.title = element_blank(),axis.text.x = element_text(color='black'),legend.position = "none") + coord_flip()
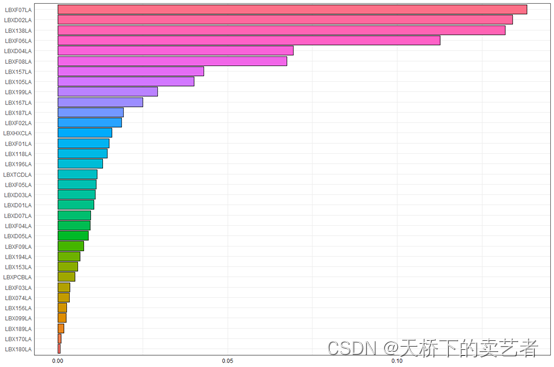
画个相关曲线图,可以看到是正相关
gwqs_scatterplot(results2i)
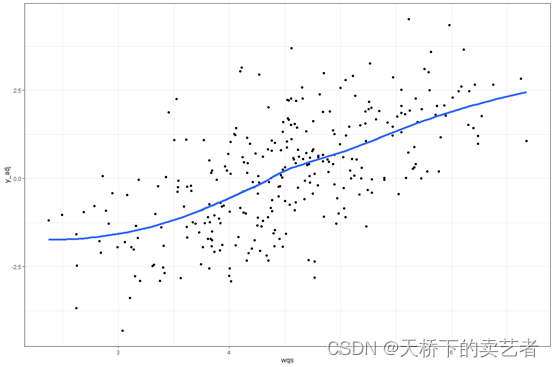
绘制残差图,可以检查它们是否随机分布在0附近或是否有趋势
gwqs_fitted_vs_resid(results2i)
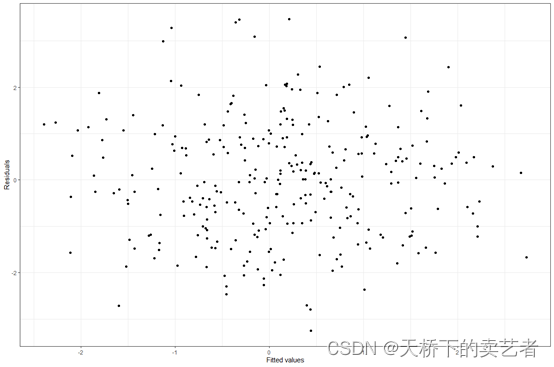
咱们还可以进行箱线图绘制,但是绘制箱线图需要使用gwqsrh函数生成下结果
results3i <-gwqsrh (y ~ wqs+sex, mix_name=PCBs, data=wqs_data,q=10, validation=0.6, b=5, b1_pos=TRUE,seed=2021,b1_constr=FALSE, family="gaussian", future.seed=TRUE)
生成结果后绘图
gWQS::gwqsrh_boxplot(results3i)
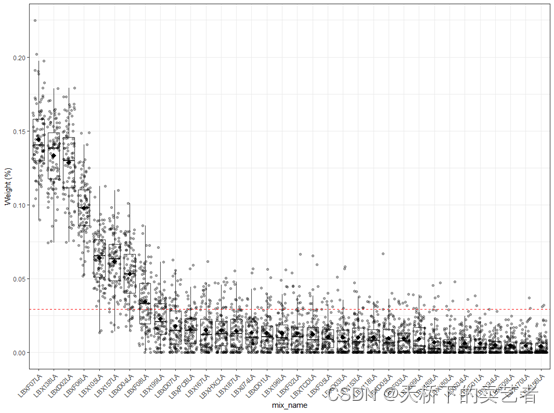
也可以使用ggplot提取数据绘图
wboxplot <- melt(results3i$wmat, varnames = c("rh", "mix_name"))wboxplot$mix_name <- factor(wboxplot$mix_name, levels = results3i$final_weights$mix_name)ggplot(wboxplot, aes(x = mix_name, y = value,fill=mix_name))+geom_boxplot()+theme_bw()+theme(axis.text.x = element_text(angle = 45, hjust = 1))
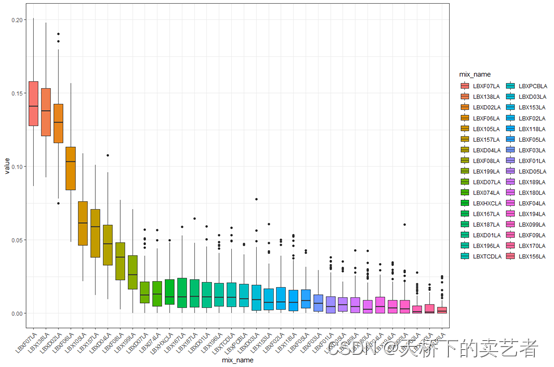
还可以调整一下
ggplot(wboxplot, aes(x = mix_name, y = value,fill=mix_name))+geom_boxplot()+theme_bw()+theme(axis.text.x = element_text(angle = 45, hjust = 1))+ylab("Weight (%)") + stat_summary(fun.y = mean, geom = "point", shape = 18, size = 3) + geom_jitter(alpha = 0.3)
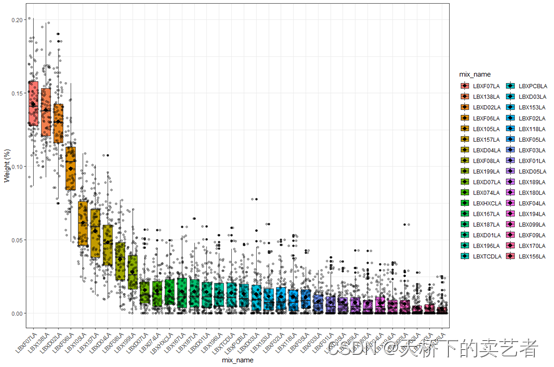
如果结局是二分类指标,咱们还可以绘制roc曲线,咱们从新生成一个结果
results4i <-gwqs (ybin ~ wqs+sex, mix_name=PCBs, data=wqs_data,q=10, validation=0.6, b=100, b1_pos=TRUE,b1_constr=FALSE, family="binomial", seed=2021)gwqs_ROC(results4i,wqs_data)
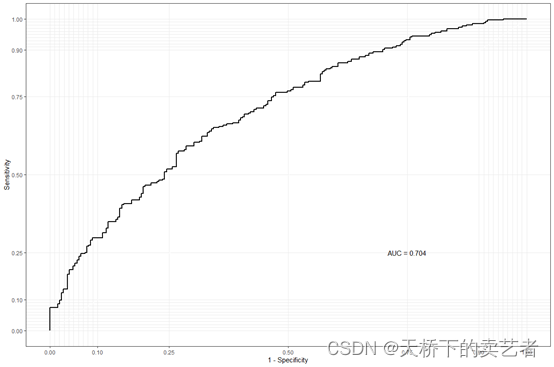
参考文献
- gwqs说明文件
- Carrico C , Gennings C , Wheeler D C ,et al.Characterization of Weighted Quantile Sum Regression for Highly Correlated Data in a Risk Analysis Setting[J].Journal of Agricultural, Biological, and Environmental Statistics, 2014.DOI:10.1007/s13253-014-0180-3.
- 李珽君,黄俊理,陈海建,莫春宝.加权分位数和回归模型的应用及R软件实现[J].预防医学,2023,35(3):275-276.DOI:10.19485/j.cnki.issn2096-5087.2023.03.021.
- https://blog.csdn.net/qq_42458954/article/details/120157806
- https://blog.csdn.net/weixin_42812146/article/details/126192945
相关文章:

R语言gWQS包在加权分位数和回归模型的应用
在流行病学研究中,相较于单一因素的暴露,多因素同时暴露的情况更为常见。传统模型在评价多因素联合暴露时存在数据维度高、多重共线性等问题. WQS 回归模型的基本原理是通过分位数间距及加权的方法,将多种研究因素的效应综合成为一个指数&…...

【Makelist】release无法生成pdb
记录makelist使用中遇到的问题 一、release版无法生成pdb 【解决方法】:需要在最大级的Makelist下的设置编译器选项添加如下标记 #release 链接库生成pdbSET(CMAKE_CXX_FLAGS_RELEASE "${CMAKE_CXX_FLAGS_RELEASE} /Zi")#lib的 release链接库生成pdbSET…...
【Linux】信号的保存和捕捉
文章目录 一、信号的保存——信号的三个表——block表,pending表,handler表sigset_t信号集操作函数——用户层sigprocmask和sigpending——内核层 二、信号的捕捉重谈进程地址空间(第三次)用户态和内核态sigaction可重入函数volat…...

Sourcepawn脚本入门(二)命令与事件监听
🍎Sourcepawn脚本入门(二)命令与事件监听 (控制台)命令是常用的插件形式,eg. noclip …等都是常用的命令,在游戏中使用也很容易,souremod可以注册自己的命令。 事件的监听则需要考虑到不同的起源游戏支持的事件不同&am…...

java-poi操作笔记
row表示行,cell表示row中的第几个cell package sample.Utils;import org.apache.poi.hssf.usermodel.HSSFWorkbook; import org.apache.poi.ss.usermodel.Cell; import org.apache.poi.ss.usermodel.DateUtil; import org.apache.poi.ss.usermodel.Workbook; impor…...

PHP:js中怎么使用PHP变量,php变量为数组时的处理
方法一:使用内嵌 PHP 脚本标记 1、简单的拼接 使用内嵌的 PHP 脚本标记 <?php ?> 将 PHP 变量 $phpVariable 的值嵌入到 JavaScript 代码中。 <?php $phpVariable "Hello, World!"; ?><script> // 将 PHP 变量的值传递给 JavaS…...
网工学习7-配置 GVRP 协议
7.1GARP概述 GARP(Generic Attribute Registration Protocol)是通用属性注册协议的应用,提供 802.1Q 兼容的 VLAN 裁剪 VLAN pruning 功能和在 802.1Q 干线端口 trunk port 上建立动态 VLAN 的功能。 GARP 作为一个属性注册协议的载体,可以用来传播属性…...

python:格式化输出指定内容
python:格式化输出指定内容 当涉及到在Python中格式化输出指定内容时,有几种方法可以让您的输出更加清晰和易读。Python的f-string(格式化字符串)是一种简洁而强大的工具,可以帮助您以所需的格式输出数据。 首先&…...

【C语言】7-35 强迫症 分数 10
7-35 强迫症 分数 10 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 小强在统计一个小区里居民的出生年月,但是发现大家填写的生日格式不统一,例如有的人写 199808,有的人只写 9808。有强迫症的小强请你写个程序,把所有人的…...
如何快速了解一家公司?
在炒股过程中,我们想要了解一家公司是否具有投资价值,需要查看和阅读很多公司的相关资料。股民们自行去查询往往会花费很多的时间精力,所以专业的炒股软件一般都会给股民提供这些现成的资料。 在金斗云智投APP内,进入到个股详情页…...

ZPLPrinter Emulator SDK for .NET 6.0.23.1123 Crack
ZPLPrinter Emulator SDK for .NET 适用于 .NET 的 ZPLPrinter 仿真器 SDK 允许您通过编写 C# 或VB.NET 代码针对任何 .NET Framework、.NET CORE、旧版 ASP.NET MVC 和 CORE、Xamarin、Mono 和通用 Windows 平台 (UWP) 作业。 适用于 .NET 的 ZPLPrinter 仿真器 SDK 允许您将…...

查收查引(通过文献检索开具论文收录或引用的检索证明)
开具论文收录证明的 专业术语为 查收查引,是高校图书馆、情报机构或信息服务机构提供的一项有偿服务。 因检索需要一定的时间,提交委托时请预留足够的检索时间。 一般需要提供:论文题目、作者、期刊名称、发表年代、卷期、页码。 目录 一、查…...

Python一帮一
在当前尚未分组的学生中,将名次最靠前的学生与名次最靠后的异性学生分为一组。 输入格式: 输入第一行给出正偶数N(≤50),即全班学生的人数。此后N行,按照名次从高到低的顺序给出每个学生的性别࿰…...

学员追访 | “IC的标签并不是只有高薪与965”
大家好,我是08期的学员小D 。 很开心能在这里与大家分享我的学习、工作经历,我毕业于一所双非本科院校。现在已经入职五个月了,很满意目前的薪资水平和工作状态。 接下来我把我的学习经历和求职经验给大家做个分享,希望能够帮到…...
LeetCode(39)赎金信【哈希表】【简单】
目录 1.题目2.答案3.提交结果截图 链接: 赎金信 1.题目 给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。 如果可以,返回 true ;否则返回 false 。 magazine 中的每个字…...

输入日期求n天后
题目要求:输入一个日期startdate年月日和days天数(>1),输出自该日期days天后的日期enddate。 要求输出和输出的年份为四位整数,输入时对输入数据的有效性进行检查;同时考虑跨月,跨年和闰年情…...
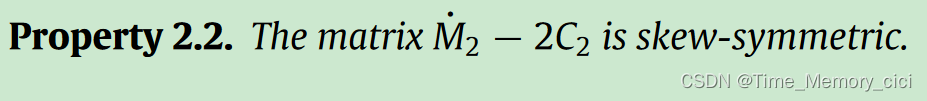
科技论文中的Assumption、Remark、Property、Lemma、Theorem、Proof含义
一、背景 学控制、数学、自动化专业的学生在阅读论文时,经常会看到Assumption、Remark、Property、Lemma、Theorem、Proof等单词,对于初学者可能不太清楚他们之间的区别,因此这里做一下详细的说明。 以机器人领域的论文为例。 论文题目&…...

逆向爬虫进阶实战:突破反爬虫机制,实现数据抓取
文章目录 一、引言二、逆向爬虫进阶技巧三、逆向爬虫进阶实战代码片段四、总结与展望好书推荐内容简介作者简介前言节选 一、引言 随着网络技术的发展,网站为了保护自己的数据和资源,纷纷采用了各种反爬虫机制。然而,逆向爬虫技术的出现&…...

个体民营诊所-如何打破传统发展瓶颈,增客流-提营收?
随着人们对传统医学和自然疗法的需求增加,开办针灸诊所可以满足社会公众对健康的需求,提供更多元化的医疗选择。 针灸作为一种传统的中医疗法,不仅可以帮助调理身体,还能帮助客户缓解疼痛,改善循环等。但针灸诊所&…...

Filament引擎分析--command抽象设备API
1. 前言 Filament中使用了FrameGraph来管理渲染管线,需要准备两点: 设备接口抽象:设备API抽象为Command资源抽象:使用虚拟资源,在实际用到时再创建,方便剔除无用资源 下面就围绕Filament中设备API抽象为…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
