【知识】稀疏矩阵是否比密集矩阵更高效?
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn]
问题提出
有些地方说,稀疏图比密集图的计算效率更高,真的吗?
原因猜想
这里的效率高,应该是有前提的:当使用稀疏矩阵的存储格式(如CSR)时,计算效率更高。如果是普通的完整矩阵格式,实际上效率一样。
稀疏矩阵的存储格式(如 COO、CSR 或 CSC)直接影响乘法的效率, 一些格式在某些类型的运算中更高效,因为它们可以更快地访问和处理非零元素。因此,当使用了稀疏矩阵存储格式时,如果矩阵非常稀疏(即大多数元素为零),那么使用稀疏矩阵进行矩阵乘法通常会更高效,因为可以跳过大量的零元素乘法操作。
代码验证
import numpy as np
from scipy.sparse import csr_matrix
import time
import matplotlib.pyplot as plt
from tqdm import tqdmdef measure_time(matrix_size=1000, density=0.1):# 创建密集矩阵dense_matrix = np.random.rand(matrix_size, matrix_size)# 创建普通的稀疏矩阵sparse_matrix = dense_matrix < densitysparse_matrix = sparse_matrix.astype(np.float64)# 将普通的稀疏矩阵转换为CSR格式csr_matrix_sparse = csr_matrix(sparse_matrix)# warmupfor _ in range(5):np.dot(sparse_matrix, sparse_matrix)# 对普通的稀疏矩阵进行矩阵乘法,并计时start_time = time.time()_ = np.dot(sparse_matrix, sparse_matrix)sparse_time = time.time() - start_time# warmupfor _ in range(5):np.dot(dense_matrix, dense_matrix)# 对密集矩阵进行矩阵乘法,并计时start_time = time.time()_ = np.dot(dense_matrix, dense_matrix)dense_time = time.time() - start_time# warmupfor _ in range(5):csr_matrix_sparse.dot(csr_matrix_sparse)# 对CSR格式的稀疏矩阵进行矩阵乘法,并计时start_time = time.time()_ = csr_matrix_sparse.dot(csr_matrix_sparse)csr_time = time.time() - start_timereturn sparse_time, dense_time, csr_time# 矩阵大小范围
sizes = np.arange(10, 1001, 10)
# 记录每种大小下的耗时
times_sparse = []
times_dense = []
times_csr = []
for size in tqdm(sizes):sparse_time, dense_time, csr_time = measure_time(matrix_size=size)times_sparse.append(sparse_time)times_dense.append(dense_time)times_csr.append(csr_time)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(sizes, times_sparse, label='sparse')
plt.plot(sizes, times_dense, label='dense')
plt.plot(sizes, times_csr, label='csr')
plt.xlabel('matrix size')
plt.ylabel('time (s)')
plt.title('matrix_size vs time')
plt.legend()
plt.show()# 稀疏度范围
density = np.arange(0, 1, 0.01)
# 记录每种大小下的耗时
times_sparse = []
times_dense = []
times_csr = []
for den in tqdm(density):sparse_time, dense_time, csr_time = measure_time(density=den)times_sparse.append(sparse_time)times_dense.append(dense_time)times_csr.append(csr_time)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(density, times_sparse, label='sparse')
plt.plot(density, times_dense, label='dense')
plt.plot(density, times_csr, label='csr')
plt.xlabel('density')
plt.ylabel('time (s)')
plt.title('density vs time')
plt.legend()
plt.show()
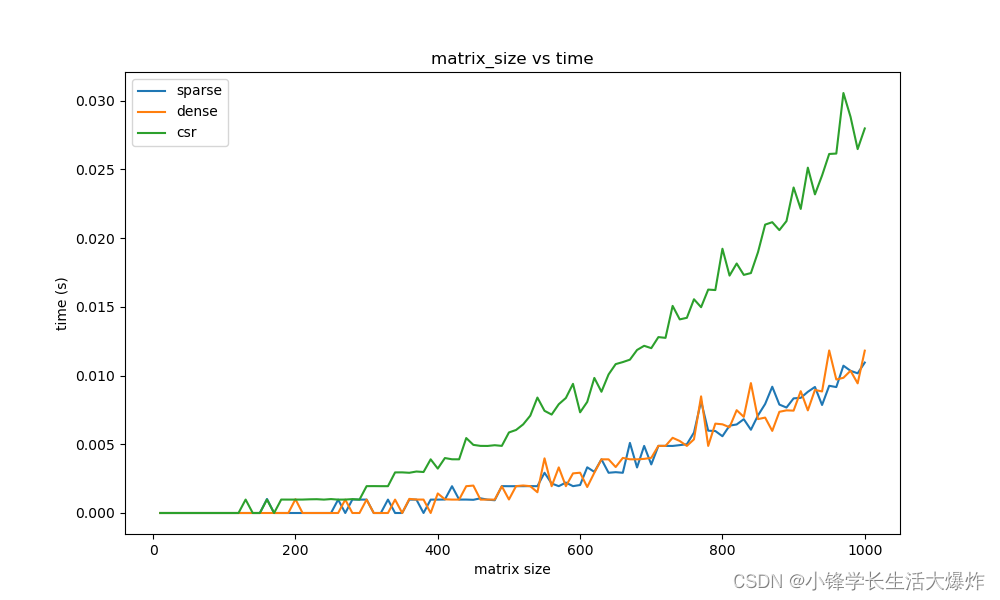
从上图可以看出,随着矩阵大小的增大,三种形式的计算效率都在降低,但两种普通的完整矩阵形式的乘法,其效率的变化趋势是一致的。考虑到时间统计有波动,因此可以看成他俩实际上是一样的时间。
注意,上图中CSR的计算效率低于其他两者,是因为密集度为0.1。当密集度设置为0.01时,CSR的计算效率就会更高了。
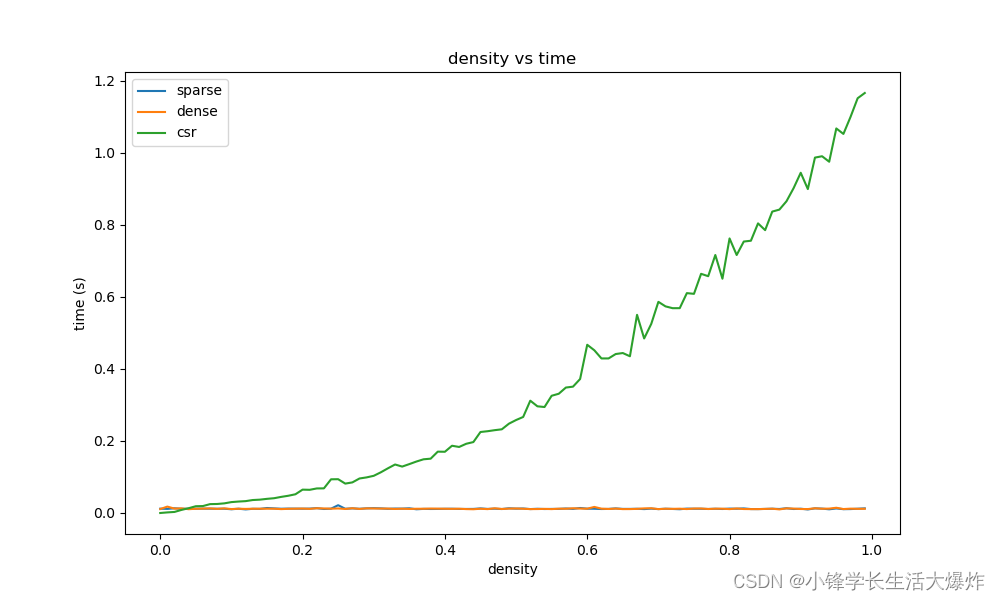
从这个图可以看到,随着密集度的增加,CSR的效率逐渐变低,但普通的完整矩阵形式的乘法,其效率并没有发生变化。
相关文章:

【知识】稀疏矩阵是否比密集矩阵更高效?
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 问题提出 有些地方说,稀疏图比密集图的计算效率更高,真的吗? 原因猜想 这里的效率高,应该是有前提的:当使用稀疏矩阵的存储格式(如CSR)时,计…...

代码随想Day24 | 回溯法模板、77. 组合
理论基础 回溯法和递归不可分割,回溯法是一种穷举的方法,通常需要剪枝来降低复杂度。回溯法有一个选择并退回的过程,可以抽象为树结构,回溯法的模板如下: void backtracking(参数) {if (终止条件) {存放结果;return;}…...

搜索与回溯算法②
求0-9的数字可以组成的所有k 位数。 def backtrack(start, path, k, n, results):"""核心函数。:param start: 下一个添加的数字的起始位置:param path: 当前构建的路径,代表一个组合:param k: 组合中所需的数字个数:param n: 可选数字的最大值:par…...
Centos图形化界面封装OpenStack Ubuntu镜像
目录 背景 环境 搭建kvm环境 安装ubuntu虚机 虚机设置 系统安装 登录虚机 安装cloud-init 安装cloud-utils-growpart 关闭实例 删除细节信息 删除网卡细节 使虚机脱离libvirt纳管 结束与验证 压缩与转移 验证是否能够正常运行 背景 一般的镜像文件在上传OpenSt…...

使用Jmeter进行http接口测试怎么做?
前言: 本文主要针对http接口进行测试,使用Jmeter工具实现。 Jmter工具设计之初是用于做性能测试的,它在实现对各种接口的调用方面已经做的比较成熟,因此,本次直接使用Jmeter工具来完成对Http接口的测试。 一、开发接…...

创建腾讯云存储桶---上传图片--使用cos-sdk完成上传
创建腾讯云存储桶—上传图片 注册腾讯云账号https://cloud.tencent.com/login 登录成功,选择右边的控制台 点击云产品,选择对象存储 创建存储桶 填写名称,选择公有读,私有写一直下一步,到创建 选择安全管理&#…...
12.3_黑马MybatisPlus笔记(上)
目录 02 03 04 05 06 07 编辑 thinking:system.out::println?编辑 thinking:list.of? 08 thinking:RequestParam和 ApiParam注解使用? thinking:RequestParam 和PathVariable的区别? 编辑 编…...

智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于寄生捕食算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.寄生捕食算法4.实验参数设定5.算法结果6.参考…...

全息图着色器插件:Hologram Shaders Pro for URP, HDRP Built-in
8个新的Unity全息图着色器,具有故障效果,扫描线,网格线,和更多其他效果!与所有渲染管线兼容。 软件包添加了一系列的全息图着色器到Unity。从基本的全息图与菲涅耳亮点,先进的全息图与两种故障效应,扫描线,文体点阵和网格线全息图! 特色全息效果 Basic-支持菲涅耳发光照…...

Python Opencv实践 - 简单的AR项目
这个简单的AR项目效果是,通过给定一张静态图片作为要视频中要替换的目标物品,当在视频中检测到图片中的物体时,通过单应矩阵做投影,将视频中的物体替换成一段视频播放。这个项目的所有素材来自自己的手机拍的视频。 静态图片&…...

Java不可变集合
Java不可变集合 不可变集合:也就是不可以被修改的集合 创建不可变集合的应用场景 ●如果某个数据不能被修改,把它防御性地拷贝到不可变集合中是个很好的实践。 ●当集合对象被不可信的库调用时,不可变形式是安全的。 简单理解࿱…...

openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复
文章目录 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复146.1 背景信息146.2 前置条件146.3 操作步骤146.4 示例 openGauss学习笔记-146 openGauss 数据库运维-备份与恢复-配置文件的备份与恢复 146.1 背景信息 在openGauss使用过程中&#x…...

一文读懂中间件
前言:在程序猿的日常工作中, 经常会提到中间件,然而大家对中间件的理解并不一致,导致了一些不必要的分歧和误解。“中间件”一词被用来描述各种各样的软件产品,在不同文献中有着许多不同的中间件定义,包括操…...

【编程基础心法】「设计模式系列」让我们一起来学编程界的“兵法”设计模式(序章)
一起来学编程界的“兵法”设计模式(序章) 设计模式是什么设计模式的概念设计模式的分类创建型模式(5种)结构型模式(7种)行为型模式(11种) 设计模式应用场景工厂模式的实现及应用单例…...

技术阅读周刊第第8️⃣期
技术阅读周刊,每周更新。 历史更新 20231103:第四期20231107:第五期20231117:第六期20231124:第七期 Prometheus vs. VictoriaMetrics (VM) | Last9 URL: https://last9.io/blog/prometheus-vs-victoriametrics/?refd…...

HTML程序大全(2):通用注册模版
一、正常情况效果 二、某项没有填写的效果 三、没有勾选同意项的效果 四、代码 <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>注册</title><style>body {font-family: Arial, sans-serif;background-color…...

【循环结构 for、break、continue高级用法】
在 C++ 中,for 循环是一种常用的循环结构,它用于重复执行代码块直到满足指定的条件。for 循环的基础用法相对简单,而高级用法则涉及更复杂的控制结构和技术。让我们探讨这些用法,并通过一些示例来加深理解。 文章目录 基础用法高级用法实战示例注意事项结合 break 和 conti…...
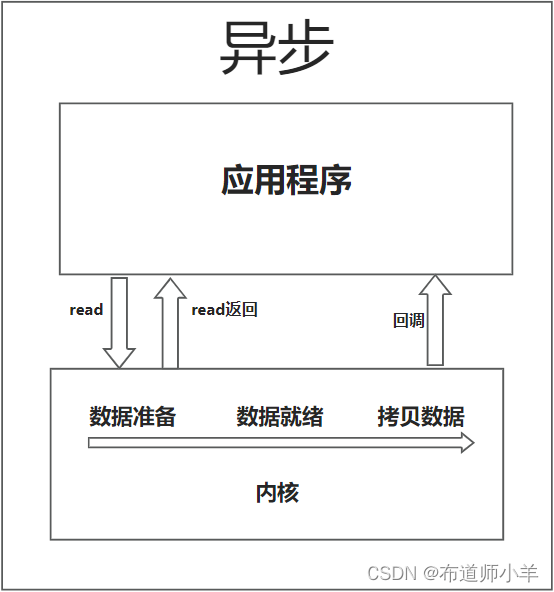
JAVA网络编程——BIO、NIO、AIO深度解析
I/O 一直是很多Java同学难以理解的一个知识点,这篇帖子将会从底层原理上带你理解I/O,让你看清I/O相关问题的本质。 1、I/O的概念 I/O 的全称是Input/Output。虽常谈及I/O,但想必你也一时不能给出一个完整的定义。搜索了谷哥欠,发…...

Linux高级系统编程-3 进程
概念 进程与程序的区别 程序:一个可执行文件, 占磁盘空间,是静态的 进程:一个程序运行的过程, 占内存,动态的。 单道程序和多道程序 单道程序设计: 所有进程一个一个排队执行。若 A 阻塞, B 只能等待࿰…...
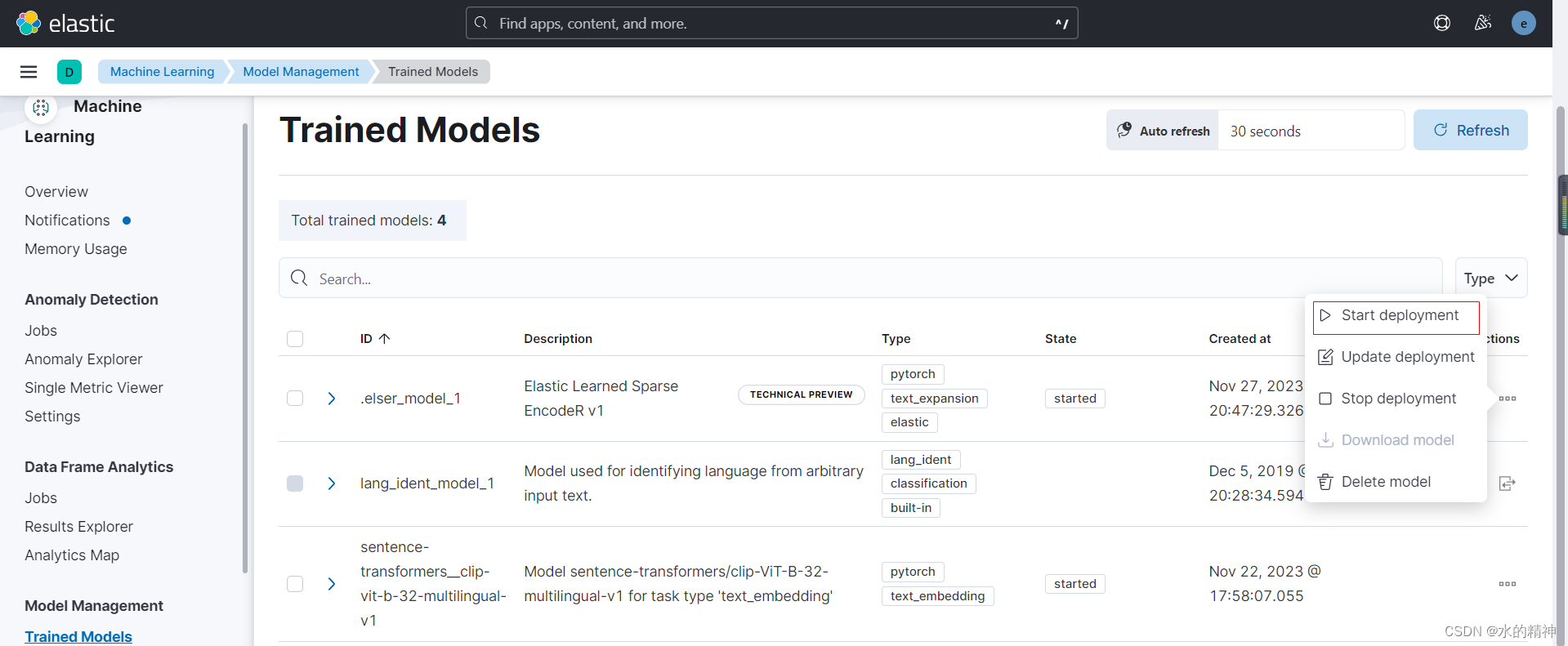
ES-ELSER 如何在内网中离线导入ES官方的稀疏向量模型(国内网络环境下操作方法)
ES官方训练了稀疏向量模型,用来支持语义检索。(目前该模型只支持英文) 最好是以离线的方式安装。在线的方式,在国内下载也麻烦,下载速度也慢。还不如用离线的方式。对于一般的生产环境,基本上也是网络隔离的…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
