大话数据结构-查找-散列表查找(哈希表)
注:本文同步发布于稀土掘金。
8 散列表查找(哈希表)
8.1 定义
散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给定值key的映射f(key),若查找集合中存在这个记录,则必定在f(key)的位置上。
这种对应关系f称为散列函数,又称为哈希(hash)函数。采用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表(Hash table),关键字对应的记录存储位置称为散列地址。
散列技术既是一种存储方法,也是一种查找方法,与线性表、树、图等结构不同,散列技术的记录之间不存在什么逻辑关系,它只与关键字有关联,因此,散列主要是面向查找的存储结构。
散列技术最适合的求解问题是查找与给定值相等的记录。但散列技术不适用于有同样关键字的情况,也不适合于范围查找。
设计一个简单、均匀、存储利用率高的散列函数是散列技术中最关键的问题,而另一个需要解决的问题是冲突——在理想情况下,每一个关键字通过散列函数计算出来的地址都是不一样的,但很多情况下会出现两个关键字key1<>key2,但f(key1)=f(key2)的情况,这种现象称为冲突(collision),key1和key2称为这个散列函数的同义词(synonym)。
8.2 散列函数的构造方法
8.2.1 直接定址法
如果我们现在要对0~100岁的人口数字统计表,那么我们对年龄这个关键字就可以直接用年龄的数字作为地址,此时f(key)=key:

如果我们现在要统计的是80后出生年份的人口数,那么我们对出生年份这个关键字可以用年份减去1980来作为地址,此时f(key)=key-1980:

也就是说,我们可以取关键字的某个线性函数值作为散列地址,即:
f ( k e y ) = a ∗ k e y + b f(key)=a * key + b f(key)=a∗key+b ( a 、 b 为常数) (a、b为常数) (a、b为常数)
这样的散列函数优点就是简单、均匀,也不会产生冲突,但问题是这需要事先知道关键字的分布情况,适合查找表较小且连续的情况。由于这样的限制,在现实应用中,此方法虽然简单,但却并不常用。
8.2.2 数字分析法
如果关键字是位数较多的数字,比如11位手机号“130xxx1234”,其中前三位是接入号,一般对应不同运营商公司的子品牌,如130是联通如意通、136是移动神州行、153是电信等;中间四位是HLR识别号,表示用户号的归属地;后四位才是真正的用户号:

若现在要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是相同的,因此选择后面的四位成为散列地址。
如果这样的抽取工作还是容易出现冲突问题,还可以对抽取出来的数字再进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环位移、甚至前现数与后两数叠加(如1234改成12+34=46)等方法。
抽取方法是使用关键字的一部分来计算散列存储位置的方法,这在散列函数中是常常用到的手段。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布比较均匀,就可以考虑使用数字分析法。
8.2.3 平方取中法
假设关键字是1234,那么它的平方就是1234*1234=1522756,再抽取中间的3位就是227,用做散列地址,而如果关键字是4321,那么它的平方就是18671041,抽取中间的3位就可以是671,也可以是710,用做散列地址。
平方取中法比较适合于不知道关键字的分布,而位数又不是很大的情况。
8.2.4 折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(注意最后一部分位数不够时可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
比如关键字是9876543210,散列表表长为3位,那么它会被分成“987”、“654”、“321”、“0”四部分,然后将它们叠加求和987+654+321+0=1962,然后根据散列表长3位,取后3位即962作为散列地址。
如果还不能够保证分布均匀,则可以对某些被分割成的部分进行反转再相加,例如将“987”反转成“789”,将“321”反转成“123”,再相加789+654+123+0=1566,再取后3位为566。
折叠法事先不需要知道关键字的分布,适合关键字位数较多的情况。
8.2.5 除留余数法
除留余数法是最常用的构造散列函数方法,对于散列表长为m的散列函数公式为:
$f(key) = key \mod p $ ( p < = m ) (p <= m) (p<=m)
例如,对一个有12个记录的数据,我们取p=11,得到如下散列表:

通常情况下,若散列表长度为m,则p一般定义为小于或等于m(最好接近m)的最小质数或不包含小于20质因子的合数。
8.2.6 随机数法
选择一个随机数,取关键字的随机函数值为它的散列地址,即:
f ( k e y ) = r a n d o m ( k e y ) f(key)=random(key) f(key)=random(key)
当关键字的长度不等时,采用随机数法构造散列函数是比较合适的。
8.2.7 总结
上文描述的构造散列函数的方法如下所示:
| 构造方法 | 描述 | 适用场景 |
|---|---|---|
| 直接定址法 | f(key) = a * key + b (a、b为常数) | 事先知道关键字的分布情况,表较小且连续的情况 |
| 数学分析法 | 观察数据,找到数据中不重复或重复度较小的部分,抽取出来直接作为散列函数,或者将抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环位移、甚至前现数与后两数叠加(如1234改成12+34=46)等,形成散列函数,如取电话号码中代表真正用户号的后四位作为散列函数 | 适合事先知道关键字的分布,且关键字的若干位分布比较均匀,且关键字位数比较大的情况 |
| 平方取中法 | 将关键字取平方,然后取中间的散列表长度数量的数字作为散列函数,例如假设关键字是1234,那么它的平方就是1234*1234=1522756,再抽取中间的3位就是227,用做散列地址,而如果关键字是4321,那么它的平方就是18671041,抽取中间的3位就可以是671,也可以是710,用做散列地址 | 适合于不知道关键字的分布,而位数又不是很大的情况 |
| 折叠法 | 将关键字从左到右分割成位数相等的几部分(注意最后一部分位数不够时可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址,比如关键字是9876543210,散列表表长为3位,那么它会被分成“987”、“654”、“321”、“0”四部分,然后将它们叠加求和987+654+321+0=1962,然后根据散列表长3位,取后3位即962作为散列地址 | 事先不需要知道关键字的分布,适合关键字位数较多的情况 |
| 除留余数法 | f(key) = key mod p (p <= m) 若散列表长度为m,则p一般定义为小于或等于m(最好接近m)的最小质数或不包含小于20质因子的合数 | 最常用的构建散列函数的方法 |
| 随机数法 | f(key)=random(key) | 当关键字的长度不等时,采用随机数法构造散列函数是比较合适的 |
8.3 处理散列冲突的方法
8.3.1 开放定址法
所谓开放定址法,就是一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入,公式是:
f i ( k e y ) = ( f ( k e y ) + d i ) m o d m f_i(key) = (f(key) + d_i) \mod m fi(key)=(f(key)+di)modm
( d i = 1 , 2 , 3...... , m − 1 ) (d_i=1,2,3......,m-1) (di=1,2,3......,m−1)
例如,关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},表长为m12,因此公式是f(key) = key mod 12。
对于关键字{12, 67, 56, 16, 25},f(key)都不会冲突,因此直接插入:

计算key=37时,发现f(37)=37%12=1,与25所在的位置冲突,于是应用公式f(37)=(f(37)+ d 1 d_1 d1) mod 12=(1+1)%12=2%12=2,将37插入到地址2:

计算key=22时,发现f(22)=22%12=10,直接插入到地址10:

计算key=29时,f(29)=29%12=5,插入到地址5:

计算key=15时,f(15)=15%12=3,插入到地址3:

计算key=47时,f(47)=47%12=11,直接插入地址11:

计算key=48时,f(48)=48%12=0,与12所在的位置冲突,于是应用公式f(48)=(f(48)+ d 2 d_2 d2) mod 12=(0+2)%12=2%12=2,冲突,应用公式f(48)=(f(48)+ d 3 d_3 d3) mod 12=(2+3)%12=5%12=5,冲突,应用公式f(48)=(f(48)+ d 4 d_4 d4) mod 12=(5+4)%12=8%12=9,将48插入到地址9:

计算key=34时,f(34)=34%12=10,冲突,应用公式f(34)=(f(34)+ d 5 d_5 d5) mod 12=(10+5)%12=15%12=3,冲突,应用公式f(34)=(f(34)+ d 6 d_6 d6) mod 12=(3+6)%12=9%12=9,冲突,应用公式f(34)=(f(34)+ d 7 d_7 d7) mod 12=(9+7)%12=16%12=3,冲突,应用公式f(34)=(f(34)+ d 8 d_8 d8) mod 12=(3+8)%12=11%12=11,冲突,应用公式f(34)=(f(34)+ d 9 d_9 d9) mod 12=(11+9)%12=20%12=8,冲突,应用公式f(34)=(f(34)+ d 1 0 d_10 d10) mod 12=(8+10)%12=18%12=6,插入到地址6:

散列表插入结束。
代码实现比较简单:
/*** generate open addressing hash table** @param array to insert array* @return inserted array* @author Korbin* @date 2023-12-06 09:10:53**/
public int[] openAddressing(int[] array) {if (null == array || array.length <= 1) {return array;}int length = array.length;int[] result = new int[length];Set<Integer> usedAddressSet = new HashSet<>();int data = 1;for (int a : array) {int mod = a % length;if (usedAddressSet.contains(mod)) {mod = (mod + data++) % length;while (usedAddressSet.contains(mod)) {mod = (mod + data++) % length;}}usedAddressSet.add(mod);result[mod] = a;}return result;
}
8.3.2 再散列函数法
事先准备好除留余数法、直接定址法、数学分析法、平方取中法、折叠法等等,在出现冲突时,随机选择一个函数重新计算地址的方式,称为再散列函数法。
8.3.3 链地址法
链地址法的实现是,存储地址存储的是单链表,当出现冲突时,把冲突的关键字存储到链表中即可,将所有关键字为同义词的记录存储在一个单链表中的表称为同义词表。
仍以关键字集合{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34}为例。
对于关键字{12, 67, 56, 16, 25},f(key)都不会冲突,因此直接插入:
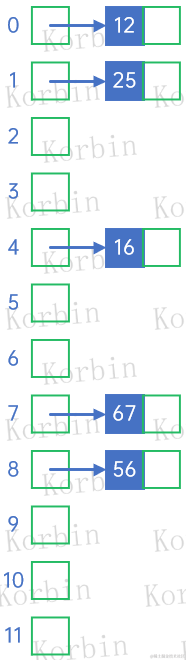
对于关键字37,f(37)=37%12=1,与25所在的地址冲突,因此将它作为25的后继结点:

对于关键字22、29、15、47,由于没有冲突,直接插入:
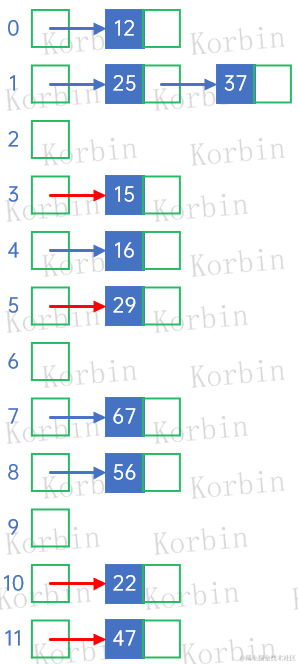
对于关键字48,f(48)=48%12=0,与12所在的地址冲突,因此将它作为12的后继结点:
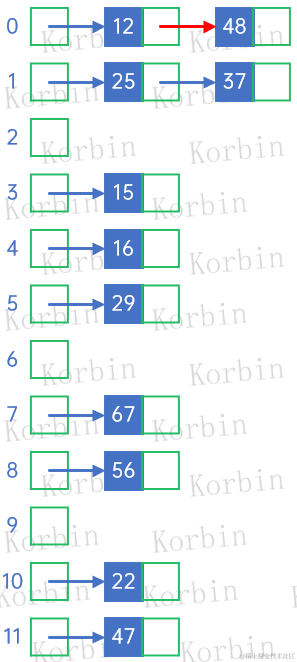
对于关键字34,f(34)=34%12=10,与22所在的地址冲突,因此将它作为22的后继结点:

插入结束。
单链表的结点定义,在大话数据结构-线性表中已有描述,链地址法的实现逻辑如下所示:
/*** generate link list addressing hash table** @param array to insert array* @return inserted array* @author Korbin* @date 2023-12-06 09:51:33**/
@SuppressWarnings("unchecked")
public LinkListNode<Integer>[] linkAddressing(int[] array) {if (null == array || array.length == 1) {return null;}int length = array.length;LinkListNode<Integer> firstNode = new LinkListNode<>(array[0]);LinkListNode<Integer>[] result = (LinkListNode<Integer>[]) Array.newInstance(firstNode.getClass(), length);for (int a : array) {int mod = a % length;if (null != result[mod]) {result[mod].setNext(new LinkListNode<>(a));} else {result[mod] = new LinkListNode<>(a);}}return result;
}8.3.4 公共溢出区法
公共溢出区法即定义多个地址表,当出现冲突时,将冲突的关键字存储到溢出表中,如下所示:
可见,公共溢出区法较适用于冲突较少的关键字存储,若冲突较多,则需要定义多个溢出表,导致大量的存储浪费。
8.4 散列表查找实现
我们只针对开放定址法和链地址法两种散列表进行查找。
对于链地址法,由于关键字存储在单链表中,因此直接使用f(key)=key%m,在查找到的单链表中查询关键字是否存在即可,若存在则返回f(key),否则返回-1表示未查找到。
对于开放定址法,仍然先使用f(key)=key%m进行定位,若该地址上的关键字与要查询的关键字不同,则令f(key)=(f(key)+1)%m,继续进行查找,但也不能无限查找下去,因此使用count计数,当整个地址表被查找过一次后,停止查找。
/*** find address of key** @param addresses addresses* @param key key to find address* @return address of key* @author Korbin* @date 2023-12-06 10:24:18**/
public int findAddress(LinkListNode<Integer>[] addresses, int key) {if (null == addresses || addresses.length == 0) {return -1;}int length = addresses.length;int mod = key % length;LinkListNode<Integer> address = addresses[mod];while (null != address) {if (address.getData() == key) {return mod;}address = address.getNext();}return -1;
}/*** find address of key** @param addresses addresses* @param key key to find address* @return address of key* @author Korbin* @date 2023-12-06 10:18:19**/
public int findAddress(int[] addresses, int key) {if (null == addresses || addresses.length == 0) {return -1;}int length = addresses.length;int mod = key % length;int count = 0;while (count < 2) {if (addresses[mod] == key) {return mod;}mod = (mod + 1) % length;if (mod == 0) {// iterate from mod to mod - 1count++;}}return -1;
}
相关文章:

大话数据结构-查找-散列表查找(哈希表)
注:本文同步发布于稀土掘金。 8 散列表查找(哈希表) 8.1 定义 散列技术是在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使得每个关键字key对应一个存储位置f(key)。查找时,根据这个确定的对应关系找到给…...

持续集成交付CICD:Sonarqube自动更新项目质量配置
目录 一、实验 1.Sonarqube手动自定义质量规则并指定项目 2.Sonarqube自动更新项目质量配置 一、实验 1.Sonarqube手动自定义质量规则并指定项目 (1)自定义质量规则 ①新配置 ②更多激活规则③根据需求激活相应规则④已新增配置 ⑤ 查看 &#x…...

Linux设置Docker自动创建Nginx容器脚本
文章目录 前言一、本地新建脚本二、复制本地脚本到服务器三、执行服务器脚本总结如有启发,可点赞收藏哟~ 前言 一、本地新建脚本 在本地新建nginx-generator.sh脚本文件,并保存以下内容 主要动态定义两个变量(容器名称/服务器本地文件名、端…...
技术博客:Vue中各种混淆用法汇总
技术博客:Vue中各种混淆用法汇总 摘要 本文主要介绍了在Vue中使用的一些常见混淆用法,包括new Vue()、export default {}、createApp()、Vue.component、Vue3注册全局组件、Vue.use()等,以及如何使用混淆器对代码进行加固,保护应…...

【python】Python生成GIF动图,多张图片转动态图,pillow
pip install pillow 示例代码: from PIL import Image, ImageSequence# 图片文件名列表 image_files [car.png, detected_map.png, base64_image_out.png]# 打开图片 images [Image.open(filename) for filename in image_files]# 设置输出 GIF 文件名 output_g…...

python/matlab图像去雾/去雨综述
图像去雾和去雨是计算机视觉领域的两个重要任务,旨在提高图像质量和可视化效果。本文将综述图像去雾和去雨的算法、理论以及相关项目代码示例。 一、图像去雾算法 基于暗通道先验的方法: 这是广泛应用于图像去雾的经典算法之一。该方法基于一个观察&…...
Docker+jenkins+gitlab实现持续集成
1.安装环境 服务器ip虚拟机版本192.168.5.132centos7.6192.168.5.152centos7.6 2. 安装docker 安装必要的一些系统工具 yum install -y yum-utils device-mapper-persistent-data lvm2添加软件源信息,要确保centos7能上外网 yum-config-manager --add-repo http:…...

Web前端JS如何获取 Video/Audio 视音频声道(左右声道|多声道)、视音频轨道、音频流数据
写在前面: 根据Web项目开发需求,需要在H5页面中,通过点击视频列表页中的任意视频进入视频详情页,然后根据视频的链接地址,主要是 .mp4 文件格式,在进行播放时实时的显示该视频的音频轨道情况,并…...
MySQL生成UUID并去除-
uuid()函数 uuid() 函数可以使mysql生成uuid,但是uuid中存在-,如下图: 去除uuid的- 默认生成的uuid含有-,我们可以使用replace函数替换掉-,SQL如下 select replace(uuid(),"-","") as uuid;Insert语句中使用UUID 如果…...

包与字符串
包是分类管理的需要,建立包用:package,包中类的引用import 学习使用javaAPI中的字符串类String,学会其成员方法的使用 (必看)eclipse包的分层等级结构设置 因为eclipse的包的结构默认是平行等级的,所以要手…...
【Gradle】mac环境安装Gradle及配置
官网安装说明:Gradle | Installation 由于Gradle运行依赖jvm,所以事先需要安装jdk,并确认你的jdk版本和gradle版本要求的对应关系,这个官网上有说明,但是我试了一下不太准确,供参考,链接如下&a…...

使用C语言操作kafka ---- librdkafka
1 安装librdkafka git clone https://github.com/edenhill/librdkafka.git cd librdkafka git checkout v1.7.0 ./configure make sudo make install sudo ldconfig 在librdkafka的examples目录下会有示例程序。比如consumer的启动需要下列参数 ./consumer <broker> &…...
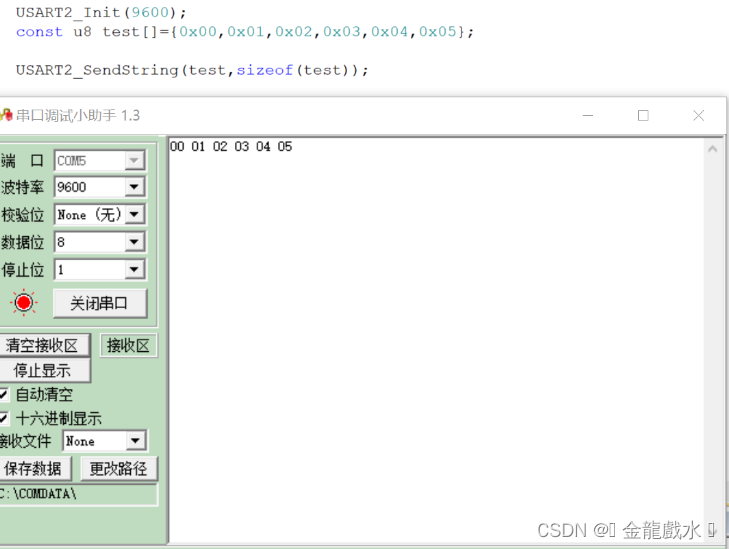
误用STM32串口发送标志位 “USART_FLAG_TXE” “USART_FLAG_TC”造成的BUG
当你使用串口发送数据时是否出现过这样的情况: 1.发送时第一个字节丢失。 2.发送时出现莫名的字节丢失。 3.各种情况字节丢失。 1.先了解一下串口发送的流程图(手动描绘): 可以假想USART_FLAG_TXE是用于检测"弹仓"&…...

指针(三)
函数指针 定义:整型指针是指向整形的指针,数组指针式指向数组的指针,其实函数指针就是指向函数的指针。 函数指针基础: ()优先级要高于*;一个变量除去了变量名,便是它的变量类型;一个指针变量…...

labelimg遇到的标签修改问题:修改一张图像的标签时,保存后导致classes.txt改变
问题描述:修改一张图像的标签时候, classes.txt 会同步更新,导致重新生成了 classes.txt 但是这个 classes.txt 只有你现在写的那个类别名,以前的没有了。 解决:设置一个 predefined_classes.txt,内容和模…...

Spring Cloud Gateway使用和配置
Spring Cloud Gateway是Spring官方基于Spring 5.0,Spring Boot 2.0和Project Reactor等技术开发的网关,Spring Cloud Gateway旨在为微服务架构提供一种简单而有效的统一的API路由管理方式。Spring Cloud Gateway作为Spring Cloud生态系中的网关ÿ…...

RT-Thread 时钟管理
时钟管理 时钟是非常重要的概念,和朋友出去游玩需要约定时间,完成任务也需要花费时间,生活离不开时间。 操作系统也一样,需要通过时间来规范其任务的执行,操作系统中最小的时间单位是时钟节拍(OS Tick&…...
User: zhangflink is not allowed to impersonate zhangflink
使用hive2连接进行添加数据是报错: [08S01][1] Error while processing statement: FAILED: Execution Error, return code 1 from org.apache.hadoop.hive.ql.exec.mr.MapRedTask. User: zhangflink is not allowed to impersonate zhangflink 有些文章说需要修…...

深入理解Sentinel系列-1.初识Sentinel
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理、分布式技术原理🔥如果感觉博主的文章还不错的话ÿ…...

vue中字典的使用
1.引入字典 dicts: [order_status,product_type],2.表单中使用 select下拉 <el-form-item label"订单状态" prop"orderStatus"><el-select v-model"form.orderStatus" clearable placeholder"请输入订单状态" :disabled"…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
