利用 Python进行数据分析实验(一)
一、实验目的
使用Python解决简单问题
二、实验要求
自主编写并运行代码,按照模板要求撰写实验报告
三、实验步骤
本次实验共有5题:
- 有四个数字:1、2、3、4,能组成多少个互不相同且无重复数字的三位数?各是多少?四个数字是2、3、7、9呢?
- 判断1000-2000之间有多少个素数,并输出所有素数.
- 打印出所有的"四叶玫瑰数",所谓"四叶玫瑰数"是指一个四位数,其各位数字四次方和等于该数本身。
- 输入一行字符,分别统计出其中英文字母、空格、数字和其它字符输出的数并分别统计每一种类型的个数。
- 打印九九乘法表。
四、实验结果
T1
T1-1
import itertoolscount = 0
for arr in itertools.permutations('1234', 3):# print(arr)print(int(arr[0]) * 100 + int(arr[1]) * 10 + int(arr[2]))count = count + 1print('共有' + str(count) + '个组合')
T1-2
import itertoolscount = 0
for arr in itertools.permutations('2379', 3):# print(arr)print(int(arr[0]) * 100 + int(arr[1]) * 10 + int(arr[2]))count = count + 1print('共有' + str(count) + '个组合')
T2
import mathcount = 0
res = []def check(x):if x <= 1:return Falsefor flag in range(2, int(math.sqrt(x) + 1)):if x % flag == 0:return Falsereturn Truefor i in range(1000, 2001):if check(i):res.append(i)count = count + 1for i in range(0, len(res)):print(res[i], end=' ')if ((i + 1) % 10) == 0:print('\n')print('\n1000~2000有素数' + str(count) + '个')
T3
def func(x):arr = str(x)if res(arr) == x:return Trueelse:return Falsedef res(arr):return pow(int(arr[0]), 4) + pow(int(arr[1]), 4) + pow(int(arr[2]), 4) + pow(int(arr[3]), 4)for i in range(1000, 10000):if func(i):print(i)T4
import recount_n = 0
count_s = 0
count_l = 0
count_o = 0'''
string = 'Some people, when confronted with a problem, ' \'think “I know, I’ll use regular expressions.” ' \'Now they have two problems.'
'''
string = input()number = re.finditer(r'\d+', string)
for match in number:count_n = count_n + 1
print('数字的数量是' + str(count_n))space = re.finditer(r'\s+', string)
for match in space:count_s = count_s + 1
print('空白的数据是' + str(count_s))letter = re.finditer(r'[a-zA-Z]', string)
for match in letter:count_l = count_l + 1
print('字符的数量是' + str(count_l))print('其他字符的数量是' + str(len(string) - count_s - count_l - count_n))
T5
import numpy as np
import itertoolscount = 0form = np.empty([81, 2], int)
for arr in itertools.product('123456789', repeat=2):form[count][0] = arr[0]form[count][1] = arr[1]count = count + 1print('打印99乘法表:')
left = 0
count = 1for i in range(0, 9):for j in range(left, left + count):string = str(form[j][0]) + '*' + str(form[j][1]) + '=' + str(int(form[j][0]) * int(form[j][1]))print('%-8s' % string, end='')print("\n")left = left + 9count = count + 1
五、实验体会
Python标准库和第三库众多,功能强大。充分利用库函数来简化和加速代码、不重复造轮子能够显著简化代码提高编码效率
相关文章:
)
利用 Python进行数据分析实验(一)
一、实验目的 使用Python解决简单问题 二、实验要求 自主编写并运行代码,按照模板要求撰写实验报告 三、实验步骤 本次实验共有5题: 有四个数字:1、2、3、4,能组成多少个互不相同且无重复数字的三位数?各是多少&…...

Jupyter Notebook工具
Jupyter Notebook 是一个交互式的笔记本环境,允许用户以网页形式编写和分享代码、文本、图像以及其它多媒体内容。它支持超过 40 种编程语言,最常用的是 Python。 以下是 Jupyter Notebook 工具的一些特点和用法: 1. 特点: 交互式…...
)
c语言上机小练(有点难)
1.题目 用指向数组的指针编程实现:输入一个字符串,内有数字和非数字符号,如:a123x456(此处一个空格)17960?302tab5876。将其中连续的数字作为一个十进制整数,依次存放到一个数组a中。例如&…...
<JavaEE> 什么是线程安全?产生线程不安全的原因和处理方式
目录 一、线程安全的概念 二、线程不安全经典示例 三、线程不安全的原因和处理方式 3.1 线程的随机调度和抢占式执行 3.2 修改共享数据 3.3 关键代码或指令不是“原子”的 3.4 内存可见性和指令重排序 四、Java标准库自带的线程安全类 一、线程安全的概念 线程安全是指…...

Kotlin 中的 also 和 run:选择正确的作用域函数
在 Kotlin 中,also 和 run 是两个十分有用的作用域函数。 虽然它们在功能上相似,但各自有独特的用途和适用场景。 一、分析: also:在对象的上下文中执行给定的代码块,并返回对象本身。它的参数是一个接收对象并返回…...
: MinRoot Example)
ZKP Understanding Nova (1): MinRoot Example
Understanding Nova Kothapalli, Abhiram, Srinath Setty, and Ioanna Tzialla. “Nova: Recursive zero-knowledge arguments from folding schemes.” Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2022. Nova: Paper Code 1. Unders…...
0基础学java-day14
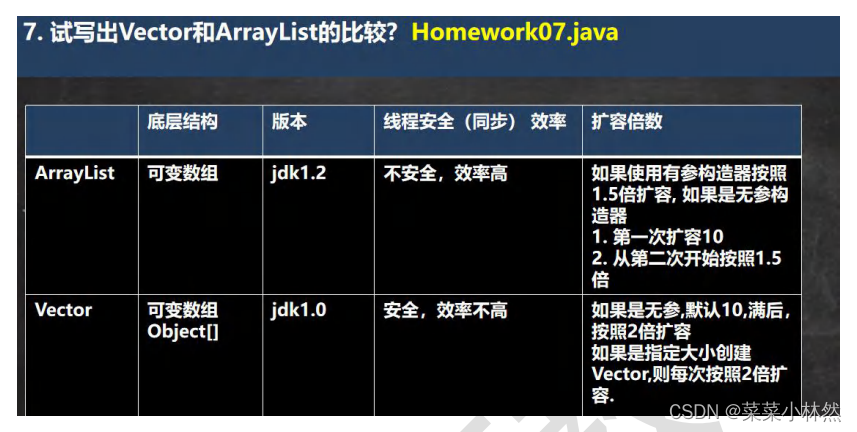
一、集合 前面我们保存多个数据使用的是数组,那么数组有不足的地方,我们分析一下 1.数组 2 集合 数据类型也可以不一样 3.集合的框架体系 Java 的集合类很多,主要分为两大类,如图 :[背下来] package com.hspedu.c…...

创建conan包-工具链
创建conan包-工具链 1 Toolchains 本文是基于对conan官方文档Toolchains翻译而来, 更详细的信息可以去查阅conan官方文档。 1 Toolchains Toolchains are the new way to integrate with build systems in Conan. Recipes can define a generate() method that wi…...
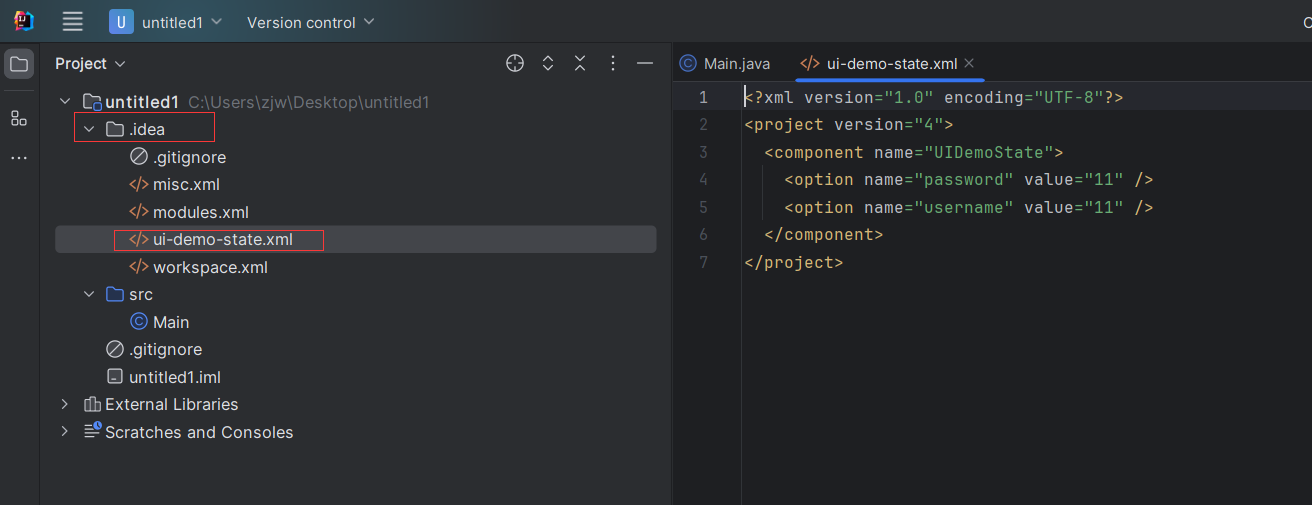
IntelliJ IDE 插件开发 | (二)UI 界面与数据持久化
系列文章 IntelliJ IDE 插件开发 |(一)快速入门 前言 在上一篇文章中介绍了在IDEA下开发、运行和安装插件的基本步骤,因此创建项目等基础步骤不再赘述,本文则开始介绍如何进行 UI 界面的开发以及相关数据的持久化存储ÿ…...

使用vue UI安装路由插件
1.使用vue创建项目 vue create vue-appvue ui 2.使用vue ui界面创建管理项目 终端页面输入:vue ui 创建项目 安装完成。可以直接在ui界面运行,也可以在编辑器中使用命令运行 安装路由,安装状态 选择插件 - 添加vue-router、添加vuex 安装…...
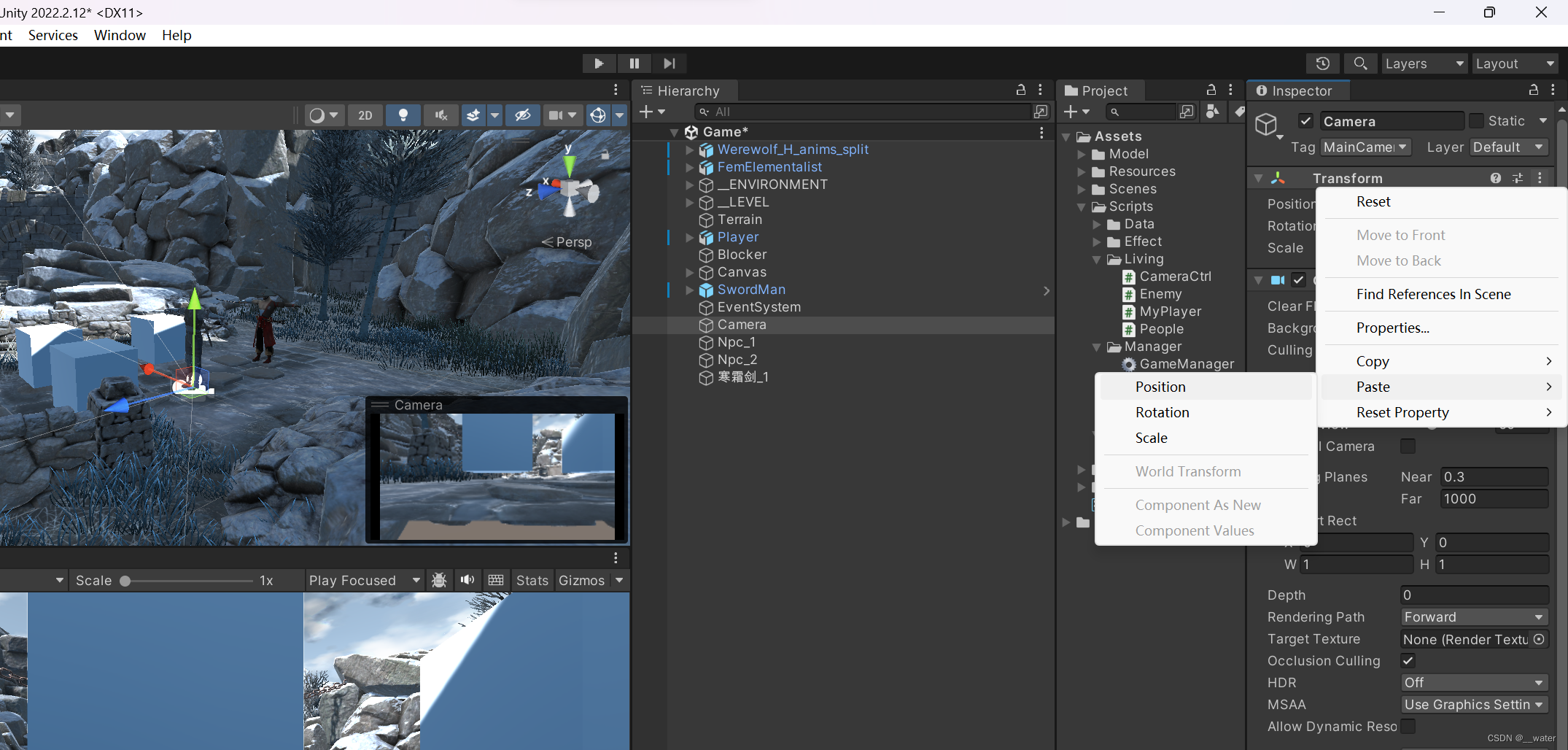
RPG项目01_脚本代码
基于“RPG项目01_场景及人物动画管理器”,我们创建一个XML文档 在资源文件夹下创建一个文件夹, 命名为Xml 将Xnl文档拖拽至文件夹中, 再在文件夹的Manager下新建脚本LoadManager 写代码: using System.Collections; using System…...

目标检测YOLO实战应用案例100讲-交通目标数据集构建及高性能检测算法研究与应用
目录 前言 国内外研究现状 目标检测研究现状 目标检测数据集研究现状...

浅谈Vue.js的计算属性computed
什么是computed属性 computed 属性用于声明计算属性,这些属性的值是基于其他响应式属性计算而来的,当依赖的响应式属性发生变化时,计算属性会自动重新计算。 与Vue.js 2相比,Vue.js 3的 computed 属性语法稍有变化,不…...

Linux常用指令详解
目录 前言: Linux的目录结构 Linux常用指令简介 whoami指令 ls指令 pwd指令 cd指令 tree指令 touch指令 mkdir指令 rmdir指令与rm指令 man指令 cp(copy)指令 mv(move)指令 cat指令 重定向及重定向的类型…...
)
Nginx(性能优化)
到这里文章的篇幅较长了,最后再来聊一下关于Nginx的性能优化,主要就简单说说收益最高的几个优化项,在这块就不再展开叙述了,毕竟影响性能都有多方面原因导致的,比如网络、服务器硬件、操作系统、后端服务、程序自身、数…...

机器学习笔记 - 如何在Python中对网格和点云进行体素化?
一、简述 本文主要是为了了解如何生成体素表示,体素之于3D就像像素之于2D。体素本质上是 3D 像素,但它们不是正方形,而是完美的立方体。 理论上,体素是复制现实的完美建模技术。 这里我们要了解四个广泛流行的 Python 库(Open3D、Trimesh、PyVista、pyntcloud )生成点云…...

冒个泡!OceanBase亮相 2023 新加坡金融科技节
近日,OceanBase 亮相 Singapore Fintech Festival 2023(2023 新加坡金融科技节)!本届新加坡金融科技节于 2023 年 11 月 15 日至 17 日在新加坡博览展览中心举行,展会期间,OceanBase 得到了众多金融科技机构…...
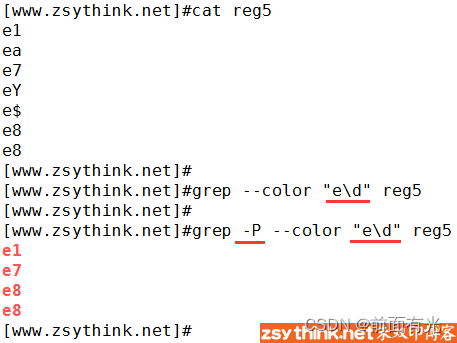
正则表达式(5):常用符号
正则表达式(5):常用符号 小结 本博文转载自 在本博客中,”正则表达式”为一系列文章,如果你想要从头学习怎样在Linux中使用正则,可以参考此系列文章,直达链接如下: 在Linux中使用正…...

Web安全漏洞分析-XSS(下)
随着互联网的迅猛发展,Web应用的普及程度也愈发广泛。然而,随之而来的是各种安全威胁的不断涌现,其中最为常见而危险的之一就是跨站脚本攻击(Cross-Site Scripting,简称XSS)。XSS攻击一直以来都是Web安全领…...
金南瓜SECS/GEM C# SDK 快速使用指南
本文对如何使用金南瓜SECS/GEM C# SDK 快速创建一个满足SECS/GEM通信要求的应用程序,只需简单3步完成。 第一步:创建C# .NET程序 示例使用Visual Studio 2010,使用者可以选择更高级版本 Visual Studio 第二步:添加DLL库引用&am…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

自然语言处理——文本分类
文本分类 传统机器学习方法文本表示向量空间模型 特征选择文档频率互信息信息增益(IG) 分类器设计贝叶斯理论:线性判别函数 文本分类性能评估P-R曲线ROC曲线 将文本文档或句子分类为预定义的类或类别, 有单标签多类别文本分类和多…...

13.10 LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析
LangGraph多轮对话系统实战:Ollama私有部署+情感识别优化全解析 LanguageMentor 对话式训练系统架构与实现 关键词:多轮对话系统设计、场景化提示工程、情感识别优化、LangGraph 状态管理、Ollama 私有化部署 1. 对话训练系统技术架构 采用四层架构实现高扩展性的对话训练…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...
