有限元中三角形的一些积分公式
文章目录
- 有限元中三角形的相关积分公式
有限元中三角形的相关积分公式
在 xyxyxy 平面中, 通过三个点 (xi,yi),(xj,yj),(xm,ym)(x_i, y_i), (x_j, y_j), (x_m, y_m)(xi,yi),(xj,yj),(xm,ym) 定义一个三角形, 令坐标原点位于其中心(或者重心),即
xi+xj+xm3=yi+yj+ym3=0\frac{x_i + x_j + x_m}{3} = \frac{y_i + y_j + y_m}{3} = 03xi+xj+xm=3yi+yj+ym=0
针对整个三角形区域的一些重要积分公式有:
∫dxdy=12∣1xiyi1xjyj1xmym∣=Δ=三角形面积\int dxdy = \frac{1}{2} \begin{vmatrix} 1 & x_i & y_i \\ 1 & x_j & y_j \\ 1 & x_m & y_m \end{vmatrix} = \Delta = 三角形面积∫dxdy=21111xixjxmyiyjym=Δ=三角形面积
∫xdxdy=∫ydxdy=0\int x dxdy = \int y dxdy = 0∫xdxdy=∫ydxdy=0
∫x2dxdy=Δ12(xi2+xj2+xm2)\int x^2 dxdy = \frac{\Delta}{12}(x_i^2 + x_j^2 + x_m^2)∫x2dxdy=12Δ(xi2+xj2+xm2)
∫y2dxdy=Δ12(yi2+yj2+ym2)\int y^2 dxdy = \frac{\Delta}{12}(y_i^2 + y_j^2 + y_m^2)∫y2dxdy=12Δ(yi2+yj2+ym2)
∫xydxdy=Δ12(xiyi+xjyj+xmym)\int xy dxdy = \frac{\Delta}{12}(x_iy_i + x_jy_j + x_my_m)∫xydxdy=12Δ(xiyi+xjyj+xmym)
相关文章:

有限元中三角形的一些积分公式
文章目录有限元中三角形的相关积分公式有限元中三角形的相关积分公式 在 xyxyxy 平面中, 通过三个点 (xi,yi),(xj,yj),(xm,ym)(x_i, y_i), (x_j, y_j), (x_m, y_m)(xi,yi),(xj,yj),(xm,ym) 定义一个三角形, 令坐标原点位于其中心(或者重心)…...

【docker-compose】安装mongodb
1. 安装方式 压缩包容器安装docker(推荐,一分钟安装) 2. 环境 linux服务器已安装好 docker docker-compose (不了解的客官,请点击进入) 3. 步骤: Step 1: linux下建立如下目录…...

【ClickHouse源码】物化视图的写入过程
本文对 ClickHouse 物化视图的写入流程源码做个详细说明,基于 v22.8.14.53-lts 版本。 StorageMaterializedView 首先来看物化视图的构造函数: StorageMaterializedView::StorageMaterializedView(const StorageID & table_id_,ContextPtr local_…...
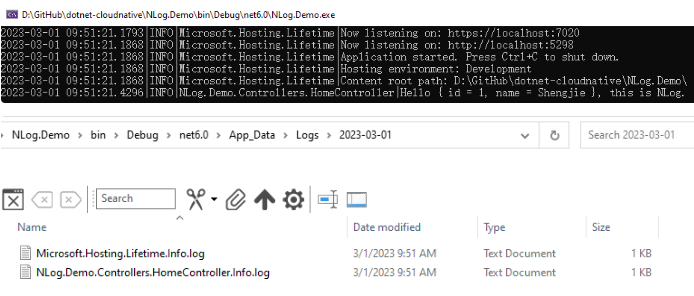
.NET 使用NLog增强日志输出
引言 不管你是开发单体应用还是微服务应用,在实际的软件的开发、测试和运行阶段,开发者都需要借助日志来定位问题。因此一款好的日志组件将至关重要,在.NET 的开源生态中,目前主要有Serilog、Log4Net和NLog三款优秀的日志组件&…...
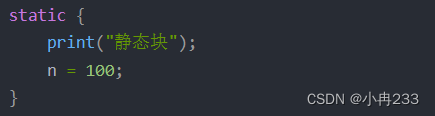
一道阿里类的初始化顺序笔试题
问题很简单,就是下面的代码打印出什么? public class InitializeDemo {private static int k 1;private static InitializeDemo t1 new InitializeDemo("t1" );private static InitializeDemo t2 new InitializeDemo("t2");priv…...

cuda找不到路径报错
编译C文件时出现:error: [Errno 2] No such file or directory: :/usr/local/cuda:/usr/local/cuda/bin/nvcc 在终端输入: export CUDA_HOME/usr/local/cuda...
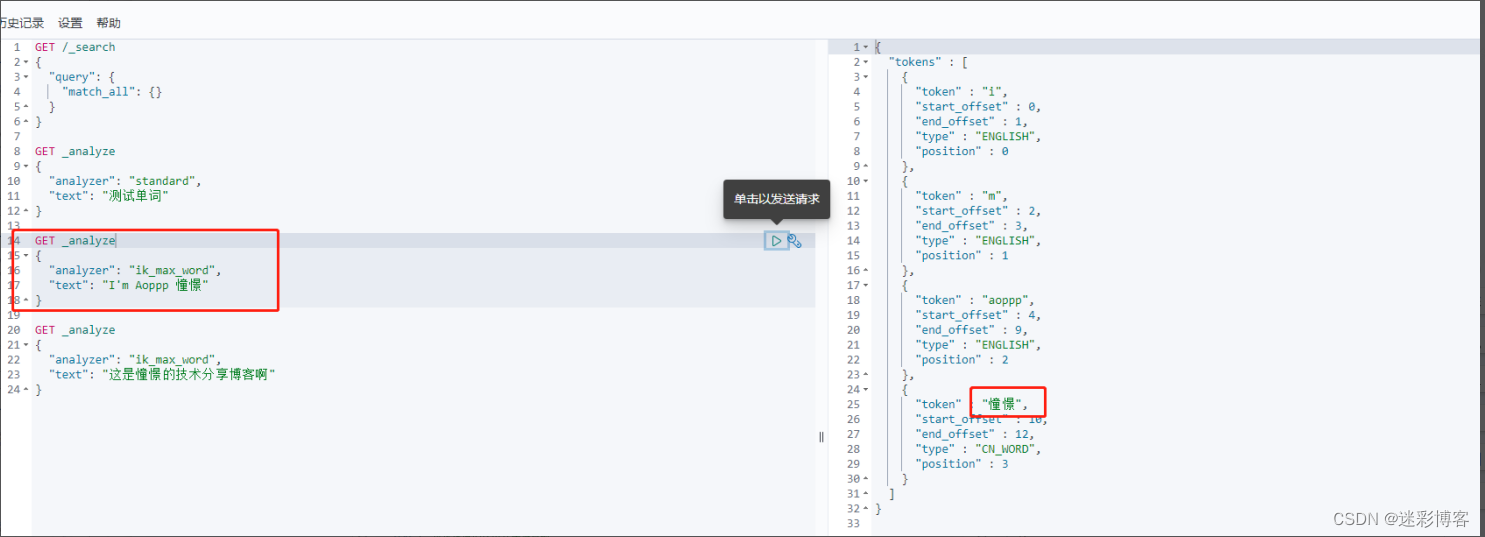
Elasticsearch进阶之(核心概念、系统架构、路由计算、倒排索引、分词、Kibana)
Elasticsearch进阶之(核心概念、系统架构、路由计算、倒排索引、分词、Kibana) 1、核心概念: 1.1、索引(Index) 一个索引就是一个拥有几分相似特征的文档的集合。比如说,你可以有一个客户数据的索引&…...

Android包体积缩减
关于减小包体积的方案: 一、所有的图片压缩,采用webp 格式。 (当然有些图片采用webp格式反而变大了,可以仍采用png格式) 二、语音资源过滤 只保留中文 resConfigs "zh-rCN", "zh” 可以减少resourc…...
)
【华为OD机试】 网上商城优惠活动(C++ Java Javascript Python)
文章目录 题目描述输入描述输出描述备注用例题目解析C++JavaScriptJavaPython题目描述 某网上商场举办优惠活动,发布了满减、打折、无门槛3种优惠券,分别为: 每满100元优惠10元,无使用数限制,如100199元可以使用1张减10元,200299可使用2张减20元,以此类推;92折券,1次…...
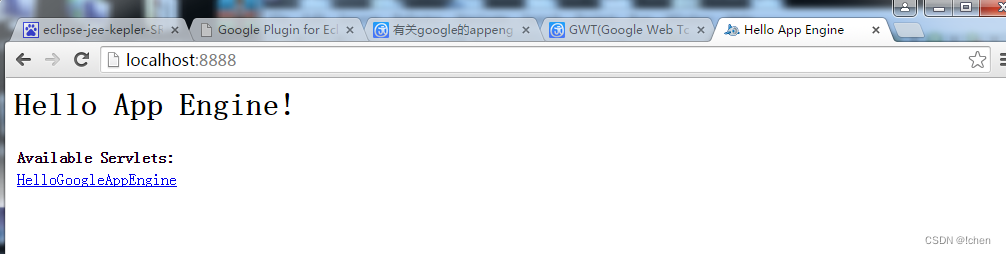
GWT安装过程
1:安装前准备 (可以问我要) appengine-java-sdk-1.9.8 com.google.gdt.eclipse.suite.4.3.update.site_3.8.0 gwt-2.5.1 eclipse-jee-kepler-SR2-win32-x86_64.zip 2:安装环境上 打开eclipse Help –Install New Software… 选择Add –…...
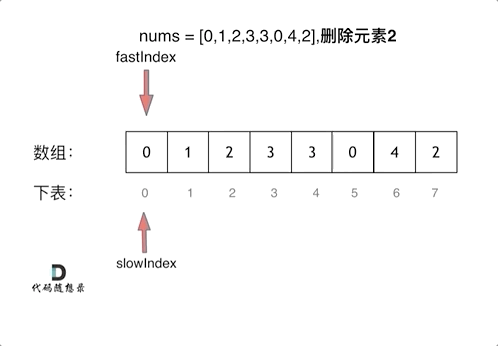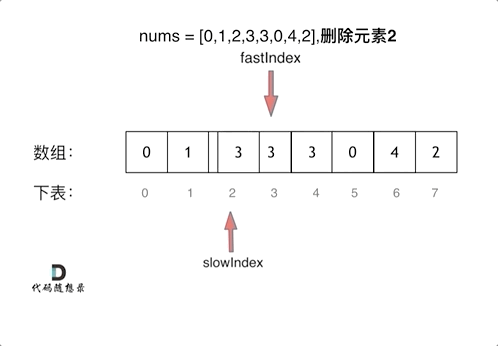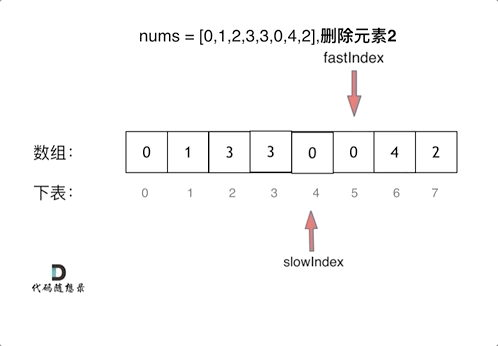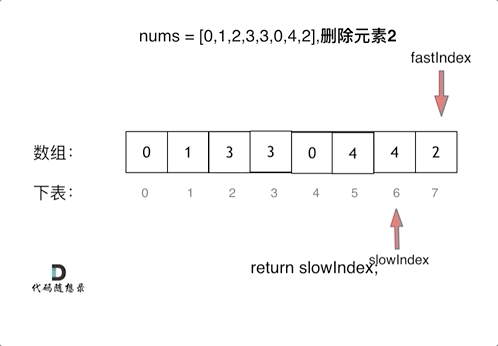
代码随想录算法训练营第一天| 704. 二分查找、27. 移除元素
Leetcode 704 二分查找题目链接:704二分查找介绍给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。思路先看看一个…...

office@word@ppt启用mathtype组件方法整理
文章目录将mathtype添加到word中ref查看office安装路径文件操作法Note附PPT中使用mathtype将mathtype添加到word中 先安装office,再安装mathtype,那么这个过程是自动的如果是先安装mathtype,再安装office,那么有以下选择: 重新安装一遍mathtype(比较简单,不需要说明)执行文件操…...
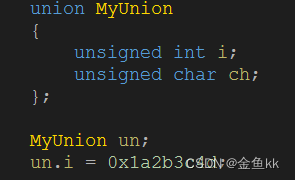
计算机大小端
我们先假定内存结构为上下型的,上代表内存高地址,下代表内存低地址。 电脑读取内存数据时,是从低位地址到高位地址进行读取(从下到上)。 1、何为大小端 大端:数据的高位字节存放在低地址,数据…...
)
Matplotlib绘图从零入门到实践(含各类用法详解)
一、引入 Matplotlib 是一个Python的综合库,用于在 Python 中创建静态、动画和交互式可视化。 本教程包含笔者在使用Matplotlib库过程中遇到的各类完整实例与用法还有遇到的库理论问题,可以根据自己的需要在目录中查询对应的用法、实例以及第四部分关于…...
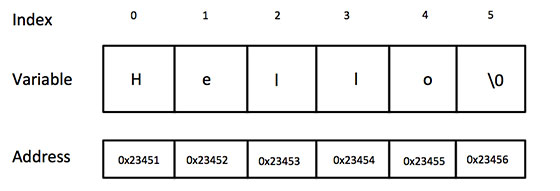
C语言 入门教程||C语言 指针||C语言 字符串
C语言 指针 学习 C 语言的指针既简单又有趣。通过指针,可以简化一些 C 编程任务的执行,还有一些任务,如动态内存分配,没有指针是无法执行的。所以,想要成为一名优秀的 C 程序员,学习指针是很有必要的。 …...

Nacos2.x+Nginx集群配置
一、配置 nacos 集群 注意:需要先配置好 nacos 连接本地数据库 1、拷贝三份 nacos 2、修改配置文件(cluster.conf) 修改启动端口: nacos1:8818 nacos2:8828 nacos3:8838 当nacos客户端升级为…...
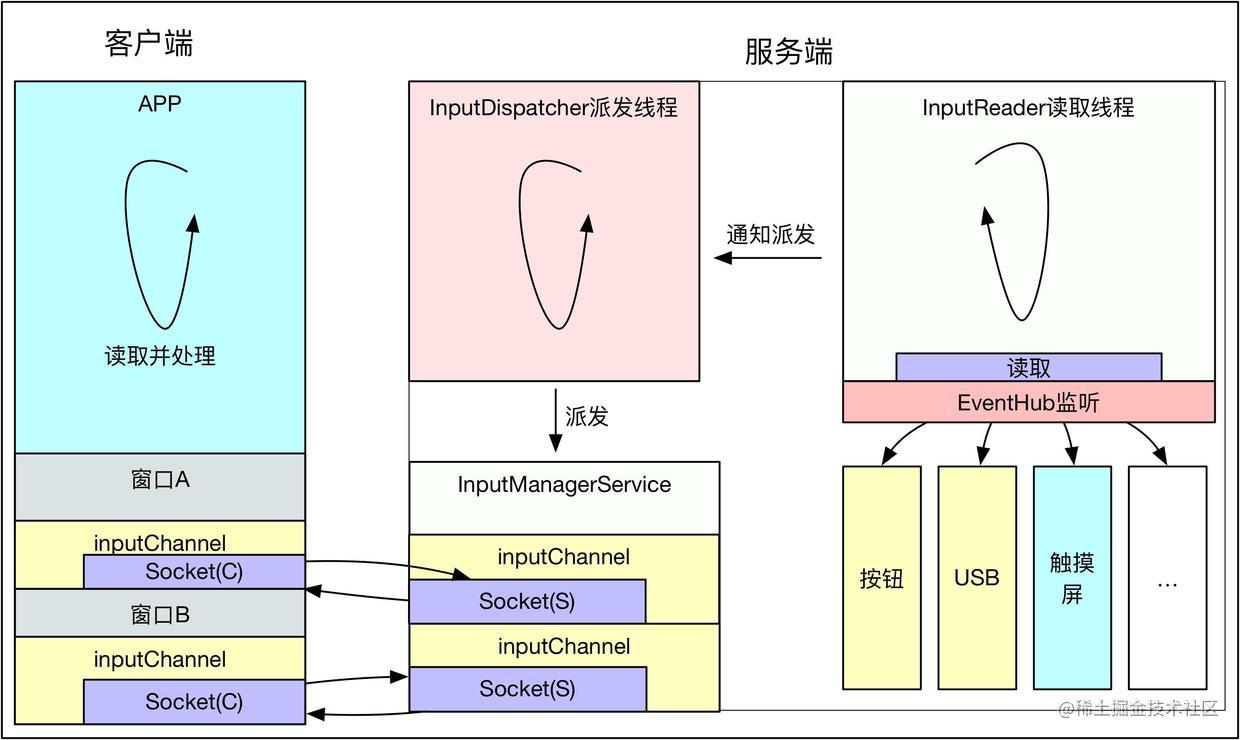
Android源码分析 - InputManagerService与触摸事件
0. 前言 有人问到:“通过TouchEvent,你可以获得到当前的触点,它更新的频率和屏幕刷新的频率一样吗?”。听到这个问题的时候我感到很诧异,我们知道Android是事件驱动机制的设计,可以从多种服务中通过IPC通信…...

python库--urllib
目录 一.urllib导入 二.urllib爬取网页 三.Headers属性 1.使用build_opener()修改报头 2.使用add_header()添加报头 四.超时设置 五.get和post请求 1.get请求 2.post请求 urllib库和request库作用差不多,但比较起来request库更加容易上手,但该了…...

美团前端二面常考react面试题及答案
什么原因会促使你脱离 create-react-app 的依赖 当你想去配置 webpack 或 babel presets。 React 16中新生命周期有哪些 关于 React16 开始应用的新生命周期: 可以看出,React16 自上而下地对生命周期做了另一种维度的解读: Render 阶段&a…...

环境搭建04-Ubuntu16.04更改conda,pip的镜像源
我常用的pipy国内镜像源: https://pypi.tuna.tsinghua.edu.cn/simple # 清华 http://mirrors.aliyun.com/pypi/simple/ # 阿里云 https://pypi.mirrors.ustc.edu.cn/simple/ #中国科技大学1、将conda的镜像源修改为国内的镜像源 先查看conda安装的信息…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
