剑指 Offer 34. 二叉树中和为某一值的路径
剑指 Offer 34. 二叉树中和为某一值的路径
难度:middle\color{orange}{middle}middle
题目描述
给你二叉树的根节点 rootrootroot 和一个整数目标和 targetSumtargetSumtargetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
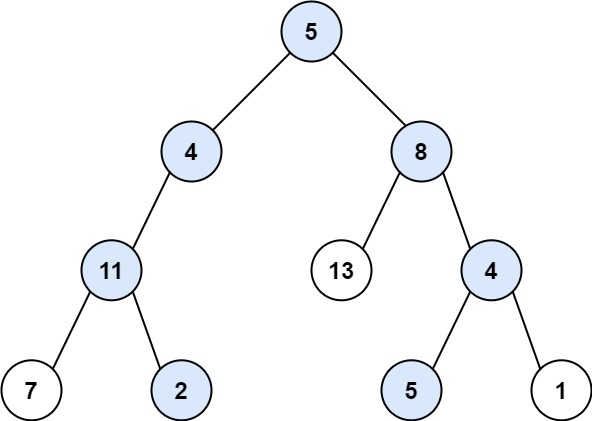
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
复制示例输入
示例 2:
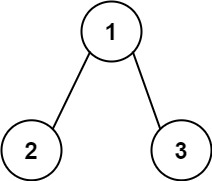
输入:root = [1,2,3], targetSum = 5
输出:[]
复制示例输入
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
复制示例输入
提示:
- 树中节点总数在范围 [0,5000][0, 5000][0,5000] 内
- −1000<=Node.val<=1000-1000 <= Node.val <= 1000−1000<=Node.val<=1000
- −1000<=targetSum<=1000-1000 <= targetSum <= 1000−1000<=targetSum<=1000
注意:本题与主站 113 题相同:https://leetcode-cn.com/problems/path-sum-ii/
算法
(递归)
- 先序遍历: 按照 “根、左、右” 的顺序,遍历树的所有节点。
- 路径记录: 在先序遍历中,记录从根节点到当前节点的路径。当路径为 ① 根节点到叶节点形成的路径 且 ② 各节点值的和等于目标值
sum时,将此路径加入结果列表。
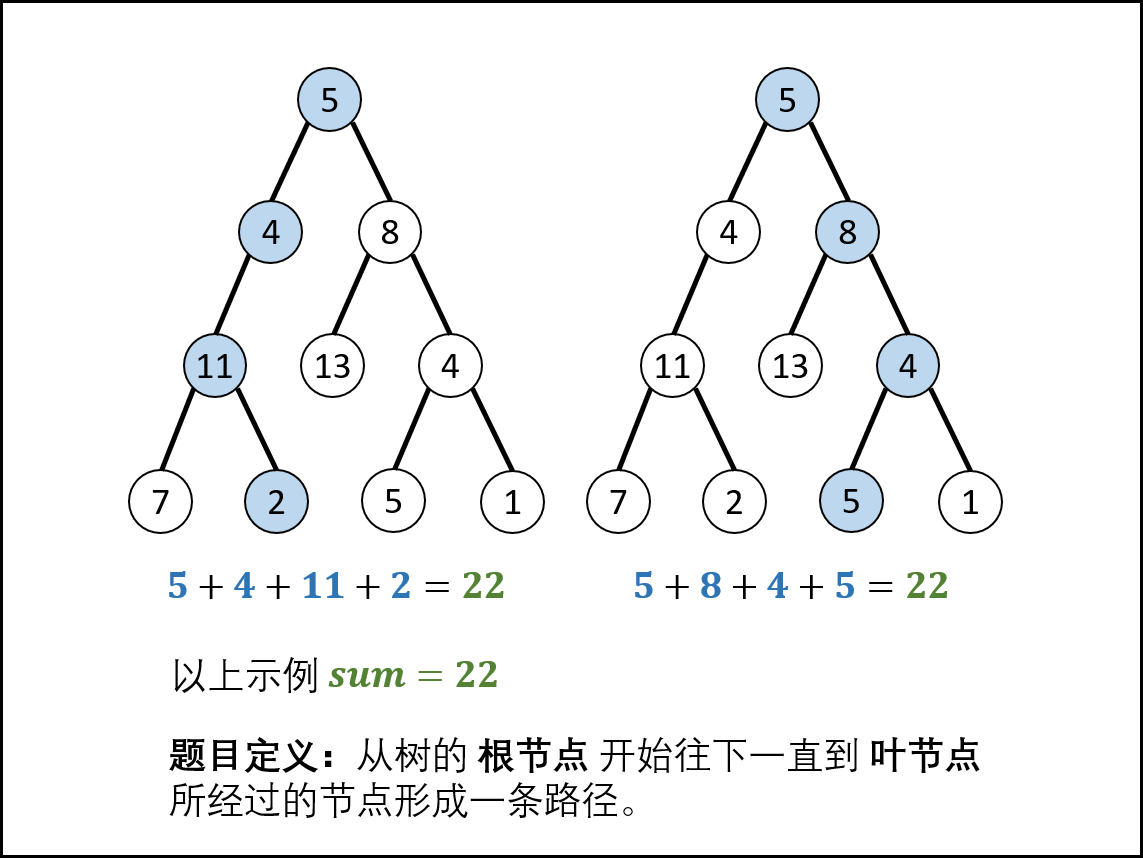
采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
复杂度分析
-
时间复杂度:O(n)O(n)O(n),其中 nnn 是二叉树的节点数。
-
空间复杂度 : O(n)O(n)O(n)
C++ 代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> path;vector<vector<int>> pathSum(TreeNode* root, int target) {dfs(root, 0, target);return res;}void dfs(TreeNode* root, int sum, int target) {if (!root) return;path.push_back(root->val);sum += root->val;if (!root->left && !root->right) {if (sum == target) res.push_back(path);} else {if (root->left) dfs(root->left, sum, target);if (root->right) dfs(root->right, sum, target);}path.pop_back();}
};
相关文章:

剑指 Offer 34. 二叉树中和为某一值的路径
剑指 Offer 34. 二叉树中和为某一值的路径 难度:middle\color{orange}{middle}middle 题目描述 给你二叉树的根节点 rootrootroot 和一个整数目标和 targetSumtargetSumtargetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 叶子节…...
2023前端vue面试题(边面边更)
Vue中key的作用 vue 中 key 值的作用可以分为两种情况来考虑: 第一种情况是 v-if 中使用 key。由于 Vue 会尽可能高效地渲染元素,通常会复用已有元素而不是从头开始渲染。因此当使用 v-if 来实现元素切换的时候,如果切换前后含有相同类型的…...

webpack配置完全指南
前言 对于入门选手来讲,webpack 配置项很多很重,如何快速配置一个可用于线上环境的 webpack 就是一件值得思考的事情。其实熟悉 webpack 之后会发现很简单,基础的配置可以分为以下几个方面: entry 、 output 、 mode 、 resolve …...
)
juju创建lxd容器时如何使用本地镜像(by quqi99)
作者:张华 发表于:2023-03-01 版权声明:可以任意转载,转载时请务必以超链接形式标明文章原始出处和作者信息及本版权声明 问题 没有外网,所以配置了一个local custom镜像库,也使用了container-image-meta…...

后端程序员学习前端开发之第一步环境搭建
一、安装 Node.js Node.js 是一个开源的、跨平台的 JavaScript 运行时环境。Node.js官网 二、安装 npm 镜像 因为 npm 是国外的,所以使用起来速度比较慢。我们这里使用了淘宝的 cnpm 镜像安装 vue。使用淘宝的 cnpm 命令管理工具代替默认的 npm 管理工具。 进入c…...

【记录问题】RuntimeError:working outside of application context. Flask使用SQLAlchemy数据库
前提:Flask使用SQLAlchemy数据库 本质:依赖包版本不匹配 问题1:报错RuntimeError:working outside of application context. 运行程序报错,如下错误: 原因:flask-sqlalchemy 版本过高导致&am…...
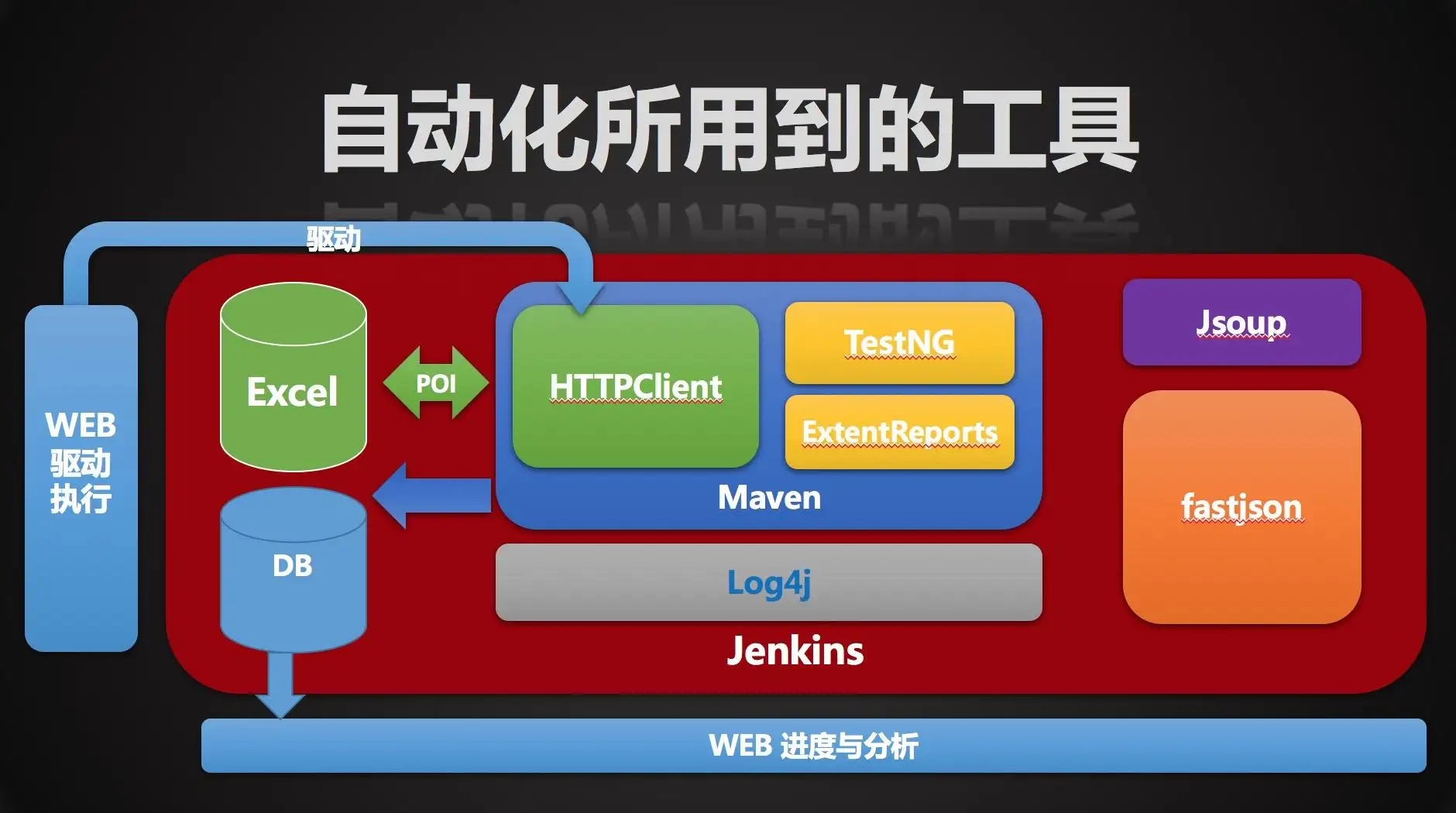
自动化测试难点案例分析,其实自动化你用错方向还不如不用
随着国内企业软件开发及测试水平的提升,许多企业开始尝试开展自动化测试的应用,以提高测试效率和测试质量。虽然在国外自动化测试工具应用已经很普遍,但国内许多企业对于软件自动化测试的理解还停留在表面上,没有深入的理解到企业…...
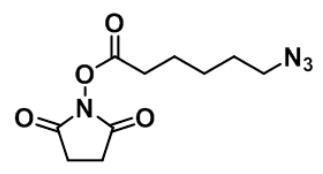
866363-70-4,N3-C5-NHS ester,叠氮-C5-NHS 主要物理性质分享
●外观以及性质:Azido-Aca-NHS淡黄色或无色油状,叠氮化物可以与炔烃、DBCO和BCN进行铜催化的点击化学反应。NHS酯可以与胺基反应,形成稳定的酰胺键。●中文名:叠氮-C5-NHS ester,6-叠氮己酸活性酯●英文名:…...
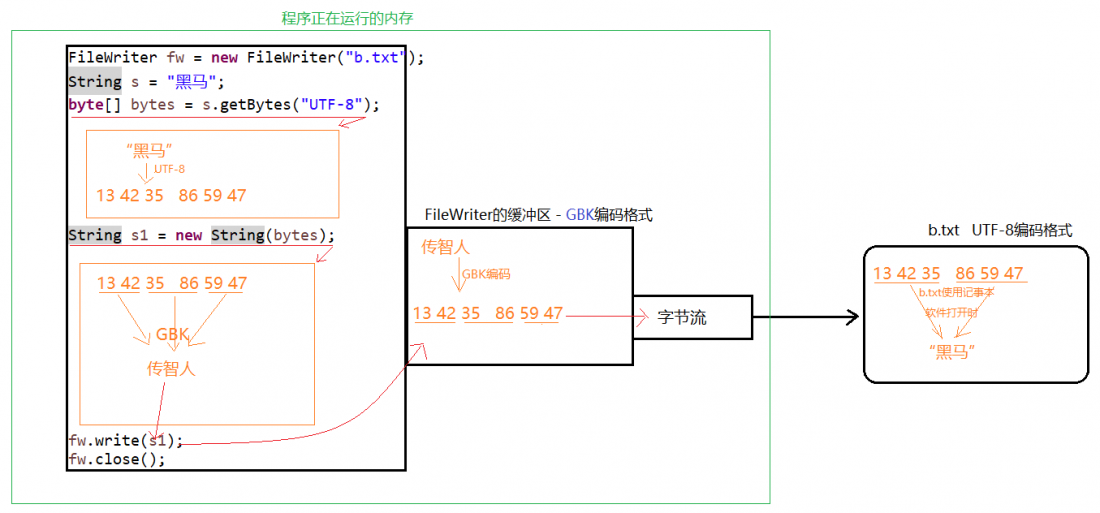
字符流定义及如何深入理解字符流的编码
IputSrem类和OupuSrem类在读写文件时操作的都是字节,如果希望在程序中操作字符,使用这两个类就不太方便,为此JDK提供了字符流。同字节流样,字符流也有两个抽象的顶级父类,分别是Reader和Writer其中,Reader是…...
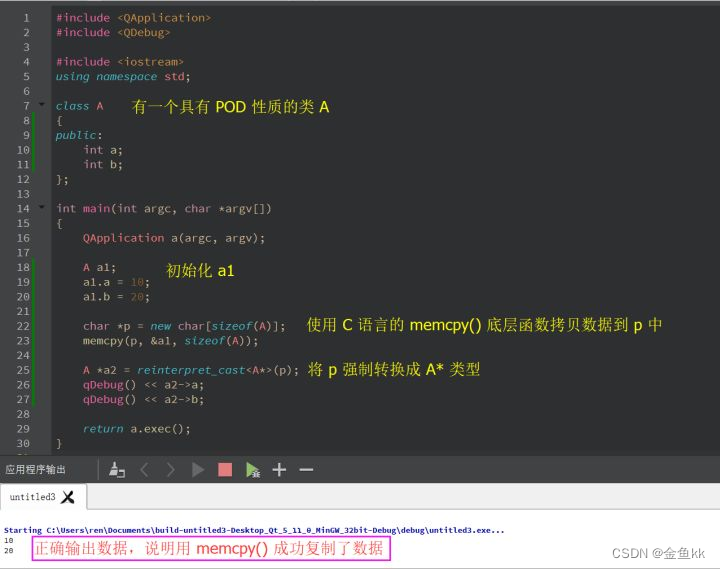
什么是pod类型
很久很久以前,C 语言统一了江湖。几乎所有的系统底层都是用 C 写的,当时定义的基本数据类型有 int、char、float 等整数类型、浮点类型、枚举、void、指针、数组、结构等等。然后只要碰到一串01010110010 之类的数据,编译器都可以正确的把它解…...
2023年中小企业实施智能制造的建议
智能制造的载体是制造系统,制造系统从微观到宏观有不同的层次,主要包括制造装备、制造单元、制造车间(工厂)、制造企业和企业生态等。随着智能制造的深入推进,未来智能制造将向以下五个方向发展。 (一&…...

【LeetCode】剑指 Offer 19. 正则表达式匹配 p124 -- Java Version
题目链接:https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/ 1. 题目介绍(19. 正则表达式匹配) 请实现一个函数用来匹配包含. 和*的正则表达式。模式中的字符.表示任意一个字符,而’*表示它前面的字符可以出现任意…...
linux和windows中安装emqx消息服务器
大家好,我是雄雄,欢迎关注微信公众号雄雄的小课堂 现在是:2023年3月1日21:53:55 前言 最近几天看了下mqtt,通过不断的搜索资料,也将mqtt集成到项目中,跑了个demo运行,和预想中的差不多&#x…...
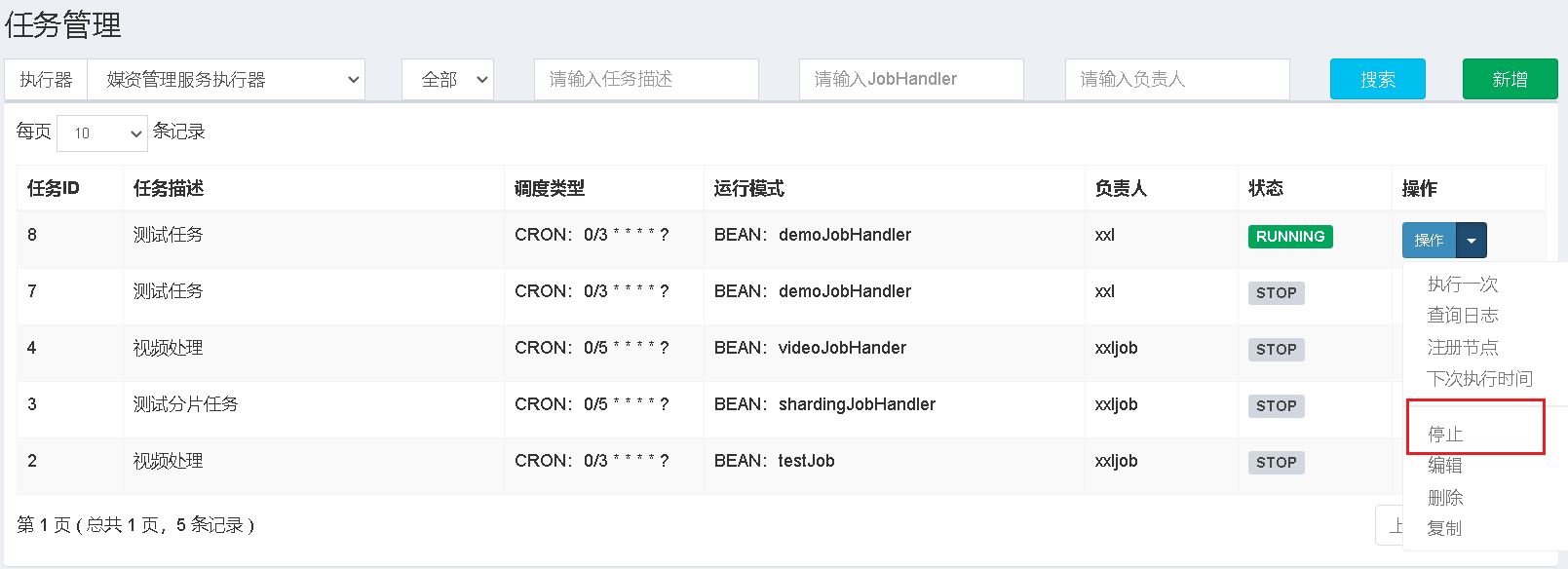
【XXL-JOB】XXL-JOB的搭建和使用
【XXL-JOB】XXL-JOB的搭建和使用 文章目录【XXL-JOB】XXL-JOB的搭建和使用1. 任务调度1.1 实现任务调度1.1.1 多线程实现1.1.2 Timer实现1.1.3 ScheduledExecutor实现2. 分布式任务调度2.1 采用分布式的原因3. XXL-JOB3.1 XXL-JOB介绍3.2 执行流程4. 搭建XXL-JOB4.1 创建数据库…...

HCIP-5OSPF基本原理及基本配置学习笔记
1、OSPF基本原理 开放式最短路径优先OSPF(Open Shortest Path First)协议是IETF定义的一种基于链路状态的内部网关路由协议。 RIP是一种基于距离矢量算法的路由协议,存在着收敛慢、易产生路由环路、可扩展性差等问题,目前已逐渐被…...

Migrate your data into databend with DataX
现在互联网应用越来越复杂,每个公司都会有多种多样的数据库。通常是用最好的硬件来跑 OLTP,甚至还在 OLTP 中进行分库分表来满足业务,这样对于一些分析,聚合,排序操作非常麻烦。这也有了异构数据库的数据同步需求&…...
)
ssh: Permission denied (publickey,gssapi-keyex,gssapi-with-mic,password)
【ansible 设置host为localhost,执行ping命令报错】 [eniq-slocalhost ansible]$ ansible all -m ping -i inventory localhost | UNREACHABLE! > { "changed": false, "msg": "Failed to connect to the host via ssh: Perm…...

有限元中三角形的一些积分公式
文章目录有限元中三角形的相关积分公式有限元中三角形的相关积分公式 在 xyxyxy 平面中, 通过三个点 (xi,yi),(xj,yj),(xm,ym)(x_i, y_i), (x_j, y_j), (x_m, y_m)(xi,yi),(xj,yj),(xm,ym) 定义一个三角形, 令坐标原点位于其中心(或者重心)…...

【docker-compose】安装mongodb
1. 安装方式 压缩包容器安装docker(推荐,一分钟安装) 2. 环境 linux服务器已安装好 docker docker-compose (不了解的客官,请点击进入) 3. 步骤: Step 1: linux下建立如下目录…...

【ClickHouse源码】物化视图的写入过程
本文对 ClickHouse 物化视图的写入流程源码做个详细说明,基于 v22.8.14.53-lts 版本。 StorageMaterializedView 首先来看物化视图的构造函数: StorageMaterializedView::StorageMaterializedView(const StorageID & table_id_,ContextPtr local_…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...
