递归-极其优雅的问题解决方法(Java)
递归的定义
大名鼎鼎的递归,相信你即使没接触过也或多或少听过,例如汉诺塔问题就是运用了递归的思想,对于一些学过c语言的同学来说,它可能就是噩梦,因为我当时就是这么认为的(不接受反驳doge)
递归到底是什么捏,递归是一种解决问题的思想它将复杂的问题转换为无数嵌套的小规模同逻辑问题,可以简化代码,使问题易于理解,要理解递归一定要先理解递归函数

递归函数
一个直接或间接调用自己的函数,就是递归函数
递归函数一定包括递归条件和基线条件,递归条件就是调用自己的条件,基线条件则是结束递归的条件
⭐太抽象了,直接通过代码理解把
递归实现阶乘
public class recurrence {public static void main(String[] args) {//递归函数调用 factorial(4);//执行步骤://递归中的 递// 1. 求factorial(4)// return 4 * factorial(3) 由于factorial(3)未知,故该问题需先求解factorial(3)// 2. 求factorial(3)// return 3 * factorial(2) 同上由于factorial(2)未知,问题又转换为求factorial(2)// 3. 求factorial(2)// return 2 * factorial(1) 同上由于factorial(1)未知,问题又转换为求factorial(1)// 4. 求factorial(1) // factorial(1)满足n = 1(满足基线条件,递归的 递 结束,开始进行 归 ) ,故factorial(1) = 1// 5. 由于factorial(1)=1得解,故factorial(2)继续执行,return 2,即factorial(2)=2// 6. factorial(2)=2,故factorial(3)=6可解// 7. factorial(3)=6,故factorial(4)=24可解// 8. 递归的 归 结束,函数结束}public static int factorial(int n){//基线条件if(n==1){return 1;}else{ //递归条件return n*factorial(n-1); }}
}
细品应该不难理解,知识输入完毕,开始输出知识,下面进入递归的应用吧
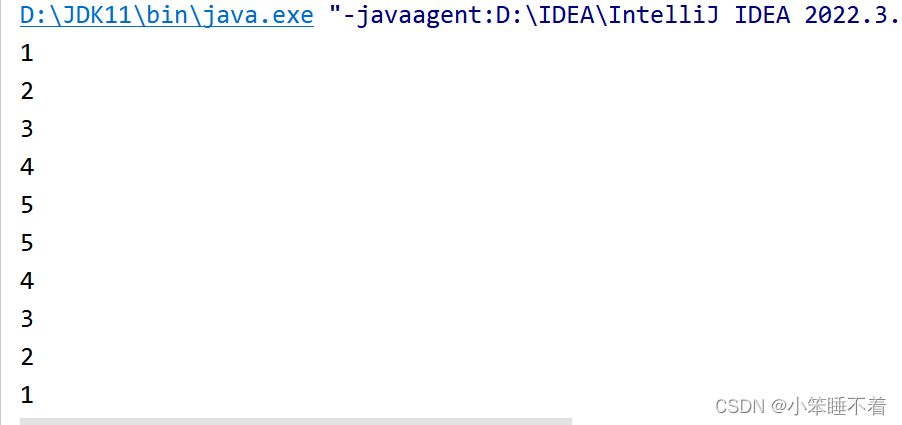
数组的正反遍历
public static void ergodic(int[] arr ,int index){//正向遍历 由递遍历System.out.println(arr[index]);//递归 if(index < arr.length-1 && 0 <= index) { //递归条件ergodic(arr , index+1);}//反向遍历 由归遍历System.out.println(arr[index]);}
使用
ergodic(new int[]{1,2,3,4,5},0);
结果
二分查找
不熟悉二分查找的可以看详解二分查找(Java)
public static int binarySearch(int[] arr, int target ,int l ,int r){if(l > r){return -1;}int mid=(l + r)>>>1; //右移运算效果为 /2if(arr[mid]<target){return binarySearch(arr,target,mid+1,r);}else if(target < arr[mid]){return binarySearch(arr,target,l,mid-1);}else{return mid;}
}
冒泡排序(优化版)
public static void bubbloSort(int[] arr , int arrSize){int greatLeft=arrSize-1;for (int i = 0; i < arrSize-1; i++) {if(arr[i] > arr[i+1]){int temp;temp=arr[i];arr[i]=arr[i+1];arr[i+1]=temp;greatLeft=i; //最后置换的位置可视为未排序的尾结点,因为后面没有置换说明后面是有序的不需要再冒泡了}}if(greatLeft!=arrSize-1){bubbloSort(arr , arrSize);}
}
插入排序
public static void insertSort(int[] arr ,int low){if(low==arr.length){return ;}for (int i = low; 0 < i; i--) {if(arr[i-1]>arr[i]){int temp=arr[i];arr[i]=arr[i-1];arr[i-1]=temp;}else {break;}}insertSort(arr,low+1);
}
多路递归
实现斐波那契数列
//斐波那契数列public static int fibonacci(int n){if(n == 0){return 0;}else if(n == 1){return 1;}return fibonacci(n-1)+fibonacci(n-2);}优化斐波那契
//(优化记忆)斐波那契数列public static int fibonacci(int n ){int[] arr =new int[n+1];Arrays.fill(arr,-1);arr[0]=0;arr[1]=1;return f(n ,arr);}private static int f(int n , int[] arr){if(arr[n]!=-1){return arr[n];}int value=f(n-1,arr)+f(n-2,arr);arr[n]=value;return value;}
尾递归
尾递归就是最后语句是函数调用语句的递归函数,尾递归可以使部分编程语言(Scala , C++)编译器对爆栈递归的进行优化,可由递归调用变为平级调用提前释放栈内存
Java不可实现,故应避免较深的递归调用而使用循环替代
分析递归的时间复杂度
主定理
其中 a为子问题数 1/b为问题规模是原来的多少倍 f(n)为其他项时间复杂度

相关文章:

递归-极其优雅的问题解决方法(Java)
递归的定义 大名鼎鼎的递归,相信你即使没接触过也或多或少听过,例如汉诺塔问题就是运用了递归的思想,对于一些学过c语言的同学来说,它可能就是噩梦,因为我当时就是这么认为的(不接受反驳doge) …...

VSCode搭建STM32开发环境
1、下载安装文件 链接:https://pan.baidu.com/s/1WnpDTgYBobiZaXh80pn5FQ 2、安装VSCodeUserSetup-x64-1.78.2.exe软件 3、 在VSCode中安装必要的插件 3、配置Keil Assistant插件 4、在环境变量中部署mingw64编译环境...
解决CentOS下PHP system命令unoconv转PDF提示“Unable to connect or start own listener“
centos系统下,用php的system命令unoconv把word转pdf时提示Unable to connect or start own listene的解决办法 unoconv -o /foo/bar/public_html/upload/ -f pdf /foo/bar/public_html/upload/test.docx 2>&1 上面这个命令在shell 终端能执行成功,…...

软件测试外包干了2个月,技术进步2年。。。
先说一下自己的情况,本科生,18年通过校招进入北京某软件公司,干了接近2年的功能测试,今年国庆,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了2年的功能测试&…...

Linux-网络服务和端口
域名:便于人们记忆和使用的标识符 www.baidu.com域名解析:将域名转换为与之对应的 IP 地址的过程 nameserver 8.8.8.8ip地址:网络设备的唯一数字标识符 域名ip地址localhost127.0.0.1 网络服务和端口 网络服务端口ftp21ssh22http80https…...
读书笔记 目录)
Kubernetes权威指南:从Docker到Kubernetes实践全接触(第5版)读书笔记 目录
完结状态:未完结 文章目录 前言第1章 Kubernetes入门 11.1 了解Kubernetes 2 附录A Kubernetes核心服务配置详解 915总结 前言 提示:这里可以添加本文要记录的大概内容: Kubernetes权威指南:从Docker到Kubernetes实践全接触&…...
阿里云Arthas使用——通过watch命令查看类的返回值 捞数据出来
前言 Arthas 是一款线上监控诊断产品,通过全局视角实时查看应用 load、内存、gc、线程的状态信息,并能在不修改应用代码的情况下,对业务问题进行诊断,包括查看方法调用的出入参、异常,监测方法执行耗时,类…...

Redis中持久化策略RDB与AOF优缺点对比
Redis持久化策略对比 RDBAOF持久化方式定时对整个内存做快照记录每一次执行的命令数据完整性不完整,两次备份之间存在丢失相对完整,取决于刷盘策略文件大小会有压缩,文件体积小记录命令,文件体积较大宕机恢复速度很快慢数据恢复优先级低,数据完整性不如AOF高,记录了执行命令数据…...
通用plantuml 时序图(Sequence Diagram)模板头
通用plantuml文件 startuml participant Admin order 0 #87CEFA // 参与者、顺序、颜色 participant Student order 1 #87CEFA participant Teacher order 2 #87CEFA participant TestPlayer order 3 #87CEFA participant Class order 4 #87CEFA participant Subject order …...

Domino多Web站点托管
大家好,才是真的好。 看到一篇文档,大概讲述的是他在家里架了一台Domino服务器,上面跑了好几个Internet的Web网站(使用Internet站点)。再租了一台云服务器,上面安装Nginx做了反向代理,代理访问…...
防火墙补充NAT
目录 1.iptables保存规则 2.自定义链 3.NAT NAT的实现分为下面类型: SNAT实验操作 DNAT实验操作 1.iptables保存规则 永久保存方法一: iptables -save > /data/iptables_rule //输出重定向备份 iptables -restore < /data/iptables_r…...

配置和管理VLAN
VLAN技术是交换技术的重要组成部分,也是交换机配置的基础。用于把物理上直接相连的网络从逻辑上划分为多个子网。 每一个VLAN 对应一个广播域,处于不同VLAN 上的主机不能通信。 不同VLAN 之间通信需要引入三层交换技术。 对性能局域网的配置和管理主要…...
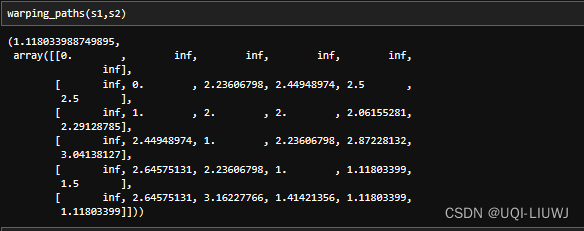
dtaidistance笔记:dtw_ndim (高维时间序列之间的DTW)
1 数据 第一个维度是sequence的index,每一行是多个元素(表示这一时刻的record) from dtaidistance.dtw_ndim import *s1 np.array([[0, 0],[0, 1],[2, 1],[0, 1],[0, 0]], dtypenp.double) s2 np.array([[0, 0],[2, 1],[0, 1],[0, .5],[0…...
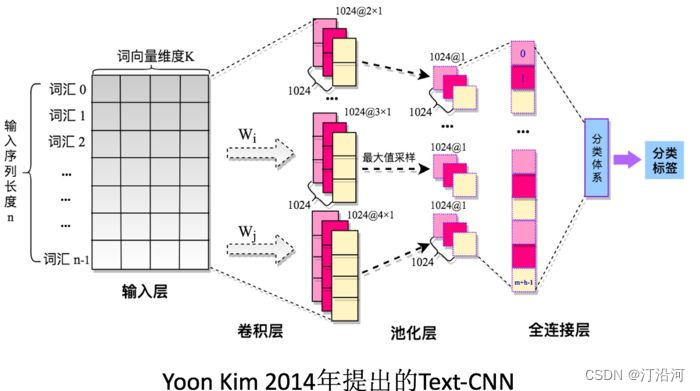
2 文本分类入门:TextCNN
论文链接:https://arxiv.org/pdf/1408.5882.pdf TextCNN 是一种用于文本分类的卷积神经网络模型。它在卷积神经网络的基础上进行了一些修改,以适应文本数据的特点。 TextCNN 的主要思想是使用一维卷积层来提取文本中的局部特征,并通过池化操…...

算法初阶双指针+C语言期末考试之编程题加强训练
双指针 常⻅的双指针有两种形式,⼀种是对撞指针,⼀种是左右指针。 对撞指针:⼀般⽤于顺序结构中,也称左右指针。 • 对撞指针从两端向中间移动。⼀个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼…...

【Spark基础】-- 宽窄依赖
目录 1、前言 2、宽窄依赖 2.1 窄依赖 2.2 宽依赖 3、宽窄转换的算子 1、前言 要理解宽窄依赖,首先我们需要了解 Transform...
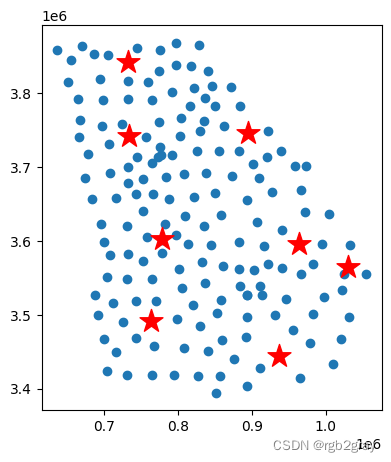
Spatial Data Analysis(六):空间优化问题
Spatial Data Analysis(六):空间优化问题 使用pulp库解决空间优化问题: pulp是一个用于优化问题的Python库。它包含了多种优化算法和工具,可以用于线性规划、混合整数线性规划、非线性规划等问题。Pulp提供了一个简单…...

PHP短信接口防刷防轰炸多重解决方案三(可正式使用)
短信接口盗刷轰炸:指的是黑客利用非法手段获取短信接口的访问权限,然后使用该接口发送大量垃圾短信给目标用户 短信验证码轰炸解决方案一(验证码类解决)-CSDN博客 短信验证码轰炸解决方案二(防止海外ip、限制ip、限制手机号次数解决)-CSDN博客 PHP短信…...
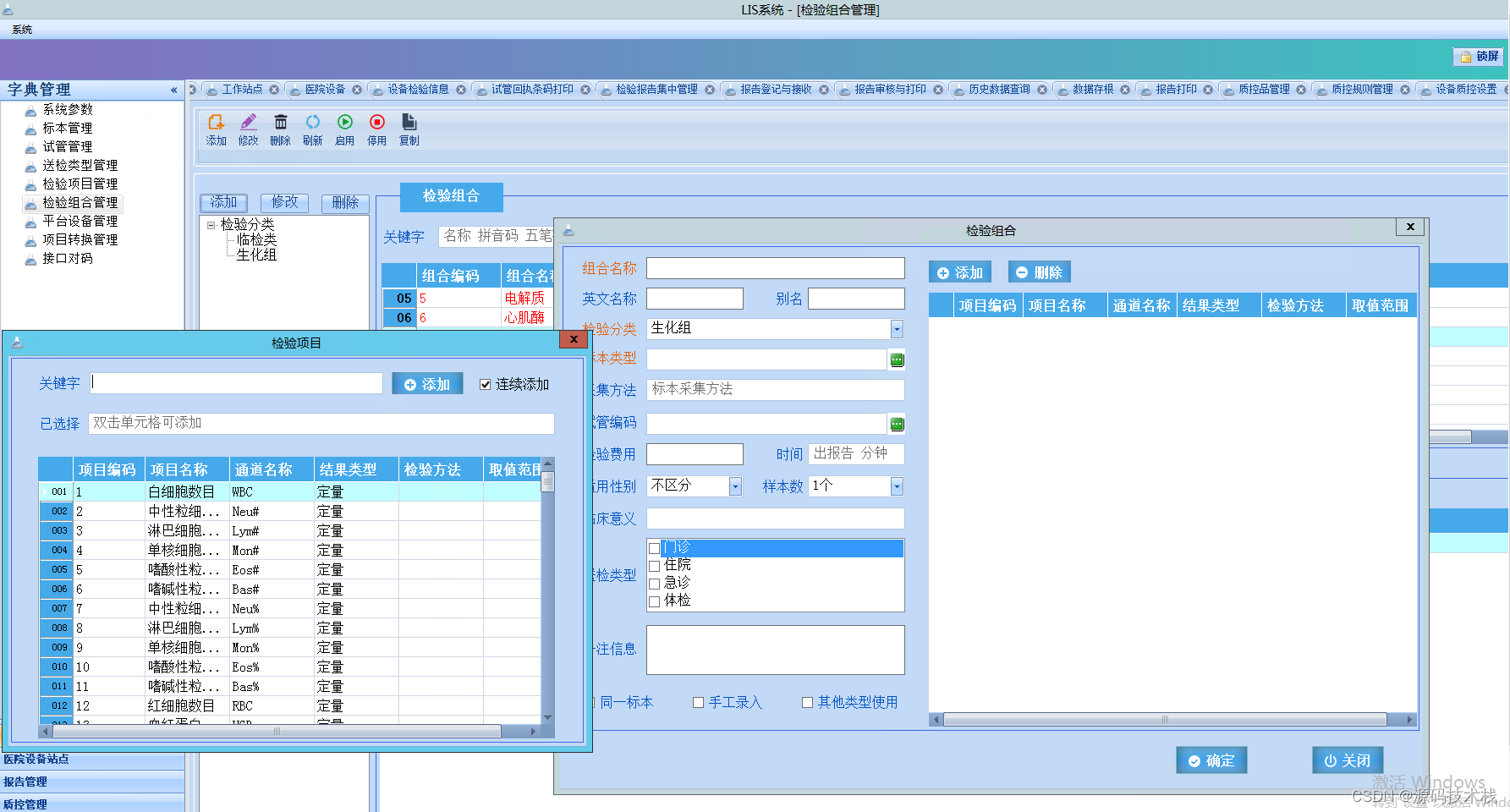
C#大型LIS检验信息系统项目源码
LIS系统,一套医院检验科信息系统。它是以数据库为核心,将实验仪器与电脑连接成网,基础功能包括病人样本登录、实验数据存取、报告审核、打印分发等。除基础功能外,实验数据统计分析、质量控制管理、人员权限管理、试剂出入库等功能…...
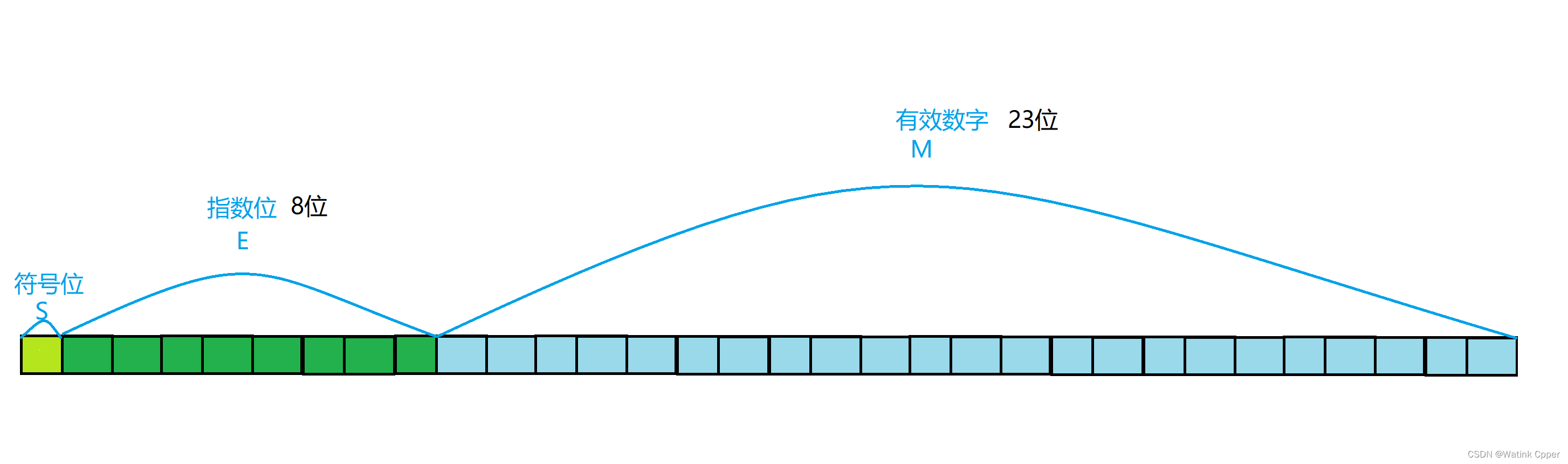
【C语言】数据在内存中的存储
目录 练笔 整型数据的存储: char 型数据——最简单的整型 整型提升: 推广到其他整形: 大小端: 浮点型数据的存储: 存储格式: 本篇详细介绍 整型数据,浮点型数据 在计算机中是如何储存的。…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...
可视化预警系统:如何实现生产风险的实时监控?
在生产环境中,风险无处不在,而传统的监控方式往往只能事后补救,难以做到提前预警。但如今,可视化预警系统正在改变这一切!它能够实时收集和分析生产数据,通过直观的图表和警报,让管理者第一时间…...
