详解线段树
前段时间写过一篇关于树状数组的博客树状数组,今天我们要介绍的是线段树,线段树比树状数组中的应用场景更加的广泛。这些问题也是在leetcode 11月的每日一题频繁遇到的问题,实际上线段树就和红黑树 、堆一样是一类模板,但是标准库里面并没有(所以题目的代码量会比较大)。如果我们深刻了解了其中的原理,刷到的时候默写出来问题也不是很大。
文章目录
- 问题引入
- 线段树的引入
- 树节点数据结构
- 建立一个线段树
- 线段树的查询
- 线段树的区间修改
- 小结
- Lazy标记
- 区间修改
- 向下传递
- 代码
- 动态开点
- 完整模板
- 总结
- 例题:
如果没有看过线段树博客的先去看那个,再来看这个问题
问题引入
在树状数组中我们的问题是:
给你一个数组 nums ,请你完成两类查询。
其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 ,其中 left <= right
实现 NumArray 类:
NumArray(int[] nums)用整数数组 nums 初始化对象void update(int index, int val)将 nums[index] 的值 更新 为 valint sumRange(int left, int right)返回数组 nums 中索引 left 和索引 right 之间( 包含 )的nums元素的 和 (即,nums[left] + nums[left + 1], …, nums[right])
在这个问题中我们对区间的修改始终是单点修改,如果我们想修改一个区间的值(指给这个区间的所有值都加、减一个数),这时候树状数组只能遍历这个区间,然后对区间每一个数做单点修改,这样修改的时间复杂度就是M*logN,M为区间长度,N为整个区间的大小。
但是如果用线段树来解决,每次区间修改的时间复杂度可以降到logN
线段树的引入
线段树不像前面介绍的树状数组一样,树状数组逻辑结构是树,但是物理结构是一个数组。而线段树是一个真正的树型结构。
假设我们有一个长度为10 的数组。如果我们要构建一个线段树一定是下面这个结构:

我们观察可以发现:
- 每个节点都是维护的一个区间的统计值(可以是区间和 区间的最大值 、最小值)
- 所有的叶子节点的区间长度均为1,也就是数组的一个单点元素的值
- 如果一个节点有子节点,且区间为
[left,right],那么子节点的区间分别为[left,mid]、[mid+1,right]其中mid=(left+right)/2
树节点数据结构
根据上图我们很轻松的就可以定义出树节点的数据结构。
struct STNode {STNode* left; // 左节点STNode* right; // 右节点int val; // 维护的区间的值(可能是区间和、区间的最值)int add; //这个是lazy标记,我们后面会介绍,这里我们可以先忽略
};
建立一个线段树
实际上这个建立树的过程,后面会讲到线段树的动态开点,否则leetcode的内存会爆掉。
假设我们给定一个数组,要求你根据这个数组构建一个线段树,这个线段树的每一个区间维护的都是这个区间的区间和。
class SegmentTree {
public:void PushUp(STNode *cur) {cur->val = cur->left->val + cur->right->val;}void BuildTree(const vector<int>& v) {N = v.size(); // 用于记录线段树查询区间的大小function<void(int,int,STNode*&)> dfs = [&](int l,int r,STNode*& cur) {if (l == r) {cur=new STNode{ nullptr,nullptr,v[l],0};return;}int mid = (r - l) / 2 + l;cur=new STNode{ nullptr,nullptr,0,0 };dfs(l, mid, cur->left);dfs(mid + 1, r, cur->right);PushUp(cur);};dfs(0, v.size() - 1, root);}
private:STNode* root = nullptr; // 根节点int N; // 用于记录线段树查询区间的大小
};
注意这个递归建立线段树,一定要选对遍历的方式——后续遍历,因为只要一个节点有子节点,那么他的值一定是在两个子节点已经遍历完了之后才能确定,这符合后续遍历的定义:先遍历完左子树和右子树,最后两个子树的信息汇总到根节点。
这样一颗完整的线段树便可以确定。注意这里的PushUp函数就是遍历完左右子树后的更新根节点,由于后面的查询和区间修改都需要这个操作所以这里需要重点理解一下!
线段树的查询
线段树查询的思路是:
假设被查询的区间是[left,right] ,当前节点的区间为 [start , end]
- 如果查询的区间正好包括了节点所代表的区间,即
left <=start && right>=end则返回区间的值 - 如果查询的区间不包含节点的区间,那么我们可以通过
mid = (start +end)/2求出其两个子节点的区间,然后将判断查询区间和哪个子节点相交,继续向子节点向下递归,直到找到第一种情况为止
对于区间查询,比方说我们需要查询[2,6]这个区间的区间和,红色的是查询的路径,蓝色是最终组成这个[2,6]区间的节点,也是查询的结束的地方。
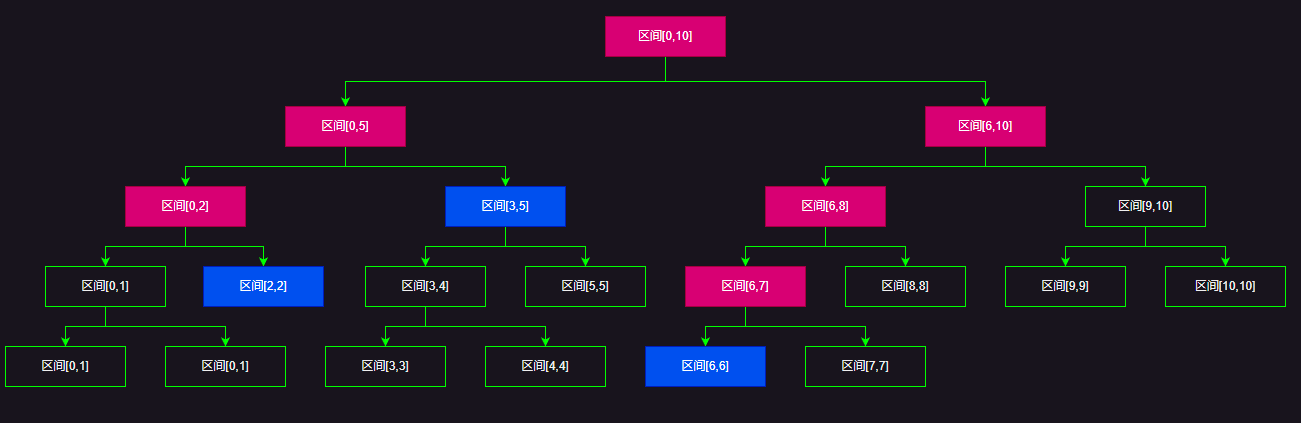
很简单,我们顺着上面的逻辑很快就能写出查询某个区间的代码,这里就不做过多的解释了
class SegmentTree {
public:void PushUp(STNode *cur) {cur->val = cur->left->val + cur->right->val;}// 区间查询int Query(int left,int right) {// left right 为要查询的区间 start end 为当前节点所维护的区间function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right,int start ,int end, STNode* cur) {if (left <= start && right >= end) {return cur->val;}int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {ansl = dfs(left, right, mid + 1, end, cur->right);}else if (right <=mid) {ansr = dfs(left, right, start, mid, cur->left);}else {ansl = dfs(left, right, mid + 1, end, cur->right);ansr = dfs(left, right, start, mid, cur->left);}//PushUp(cur); // 向上更新return ansl + ansr;};return dfs(left, right, 0, N, root);}
private:STNode* root = nullptr; // 根节点int N; // 用于记录线段树查询区间的大小
};
线段树的区间修改
这里我们讨论的区间修改只的是让区间[left,right] 都加上或减去一个val
到这里我们来分析一下如何进行区间修改,这里我们和区间查询的思路一致:
假设被查询的区间是[left,right] ,当前节点的区间为 [start , end]
- 如果查询的区间正好包括了节点所代表的区间,即
left <=start && right>=end则更新区间的值,但是这里注意,我们更新了大区间的值,下面他的所有小区间都需要更新 ,下面的代码PushDown函数就是处理这个问题的。 - 如果查询的区间不包含节点的区间,那么我们可以通过
mid = (start +end)/2求出其两个子节点的区间,然后将判断查询区间和哪个子节点相交,继续向子节点向下递归,直到找到第一种情况为止
class SegmentTree {
public:void PushUp(STNode *cur) {cur->val = cur->left->val + cur->right->val;}void PushDown(int l,int r,STNode* cur,int val) {if (cur == nullptr) {return;}cur->val += (r - l+1) * val;int mid = (r - l) / 2 + l;PushDown(l, mid, cur->left, val);PushDown(mid + 1, r, cur->right, val);}void Update(int left, int right,int val) {// left right 为要查询的区间 start end 为当前节点所维护的区间 val为区间修改的值function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {if (left <= start && right >= end) {PushDown(start, end, cur, val); // 将cur区间所有子节点全部更新了return;}int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {dfs(left, right, mid + 1, end, val, cur->right);}else if (right <= mid) {dfs(left, right, start, mid, val, cur->left);}else {dfs(left, right, mid + 1, val, end, cur->right);dfs(left, right, start, mid, val, cur->left);}PushUp(cur); // 向上更新 值,因为修改了子区间 其所有父区间都会被修改!};dfs(left, right, 0, N,val, root);}
private:STNode* root = nullptr; // 根节点int N; // 用于记录线段树查询区间的大小
};
小结
代码写到这里,线段树的功能已经被我们全部实现了,但是我们回国头来看一下线段树的实现思路,看看是否还有优化的地方。
我们主要把目光放在 线段树的修改上面,我们上面线段树的修改的思路实际上和树状数组的遍历区间的单点修改是没有什么区别的,并没有什么优势,时间复杂度都是:时间复杂度就是M*logN,M为区间长度,N为整个区间的大小。
所以我们接下来要介绍一下优化方案——Lazy标记
Lazy标记
区间修改
我们的区间修改 的优化方案 主要集中在PushDown这个函数上,我们当前的区间修改,对于节点的区间被查询区间包含的情况,是修改当前节点,并将修改传递给当前节点的每一个子节点。而我们的Lazy标记实际上就是优化这一步。
实际上我们发现我们修改完当前的节点时候(对于节点的区间被查询区间包含的情况),实际上并不需要将子节点修改,或者换一种说法:不需要立刻修改所有的子节点,我们可以设置一个Lazy标记。
这个Lazy标记的定义是:
记录所有子节点的区间应当被修改,但是未被修改的值。(这些值先由父节点记录,等到后面如果要访问到下面的节点的时候,顺路把标记带下去)
这些懒标记,我们可以在后面查询的时候,比方说访问到懒标记所在节点的子节点的时候,在去把Lazy标记下放,也就是把Lazy标记传递到子节点。
假设我有一个全0的长度位10 的数组,需要更新区间[0,6]
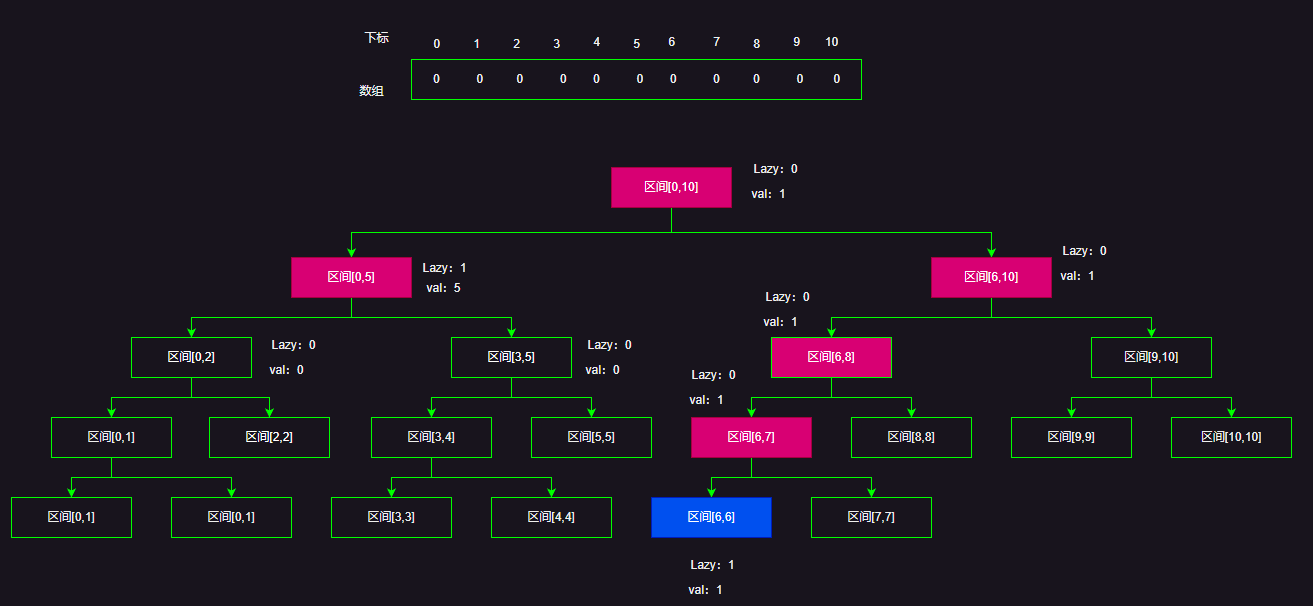
这时候按照 Lazy标记的 定义,我们遍历到区间包含节点区间的时候,就不必向下更新了,而是直接修改节点的Lazy标记,
这样
我们回过头来看,树节点的设计中我们一直都留着一个add,这个就是每个树节点的Lazy标记
struct STNode {STNode* left;STNode* right;int val;int add; // Lazy标记
};
我们更新[0,6]这个区间,递归结束的节点始终满足节点区间被查询区间所包含,注意更新的值为:区间长度*val
但是别忘了最后的回溯更新,所以这次区间更新的最终结果是,黄色的线代表回溯更新的路线
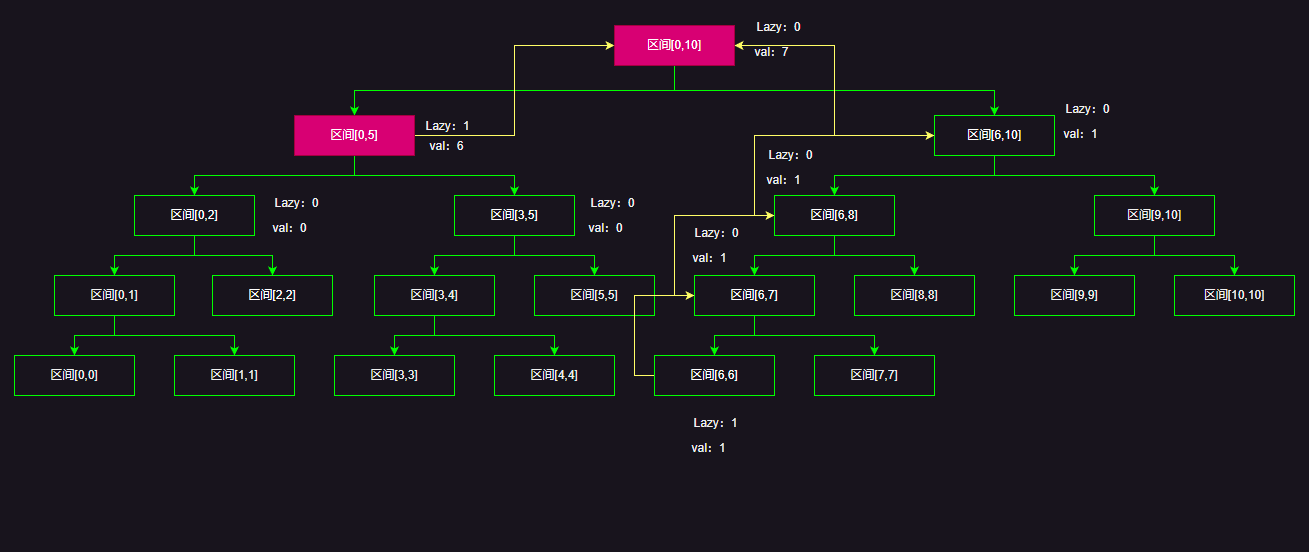
向下传递
假设我们这时候需要查询或者更新[0,2]
我们这里以更新区间[0,2],让区间里面的每一个元素加1为例:
当我们遍历到区间[0,2]的时候,这时候就需要下放Lazy标记到他的子节点,注意这里下放的Lazy标记代表节点区间[0,2]和节点区间[3,5]理论上应该区间每一个元素+1,所以每个节点的val需要+3,然后两个子节点lazy标记需要加上父节点的Lazy标记(注意不是直接赋值),因为这两个子节点的子节点并没有更新Lazy标记。最后记得把父节点区间[0,5]的lazy标记置0!
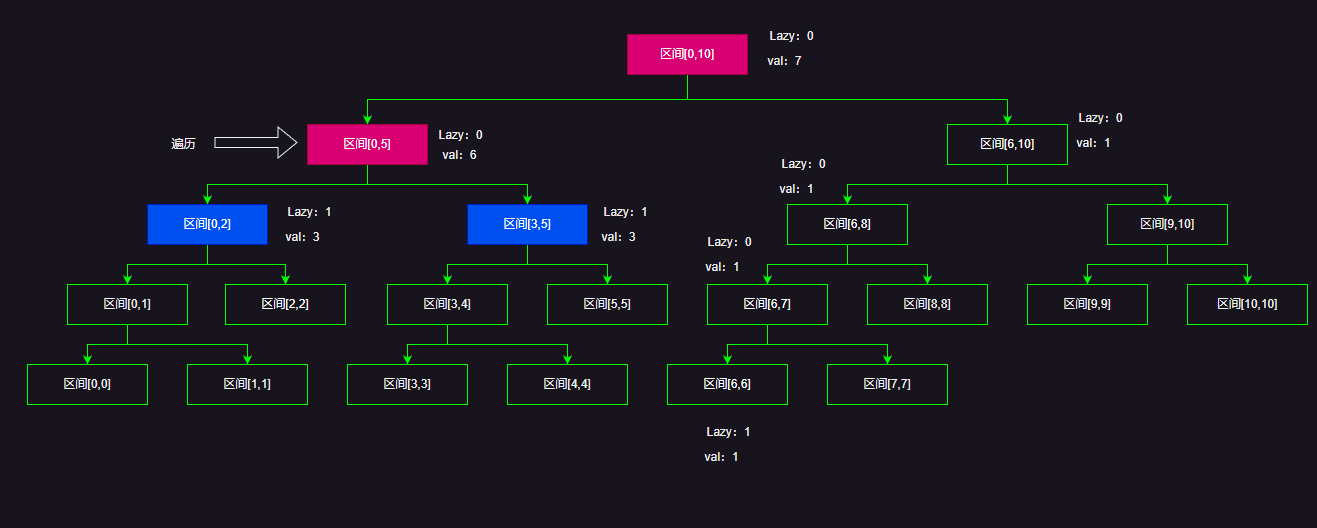
然后由于我们还需要更新[0,2]节点的值,所以我们直接更新节点区间[0,2]lazy标记,让Lazy标记+=1(因为要更新区间[0,2]让区间每一个元素加1)
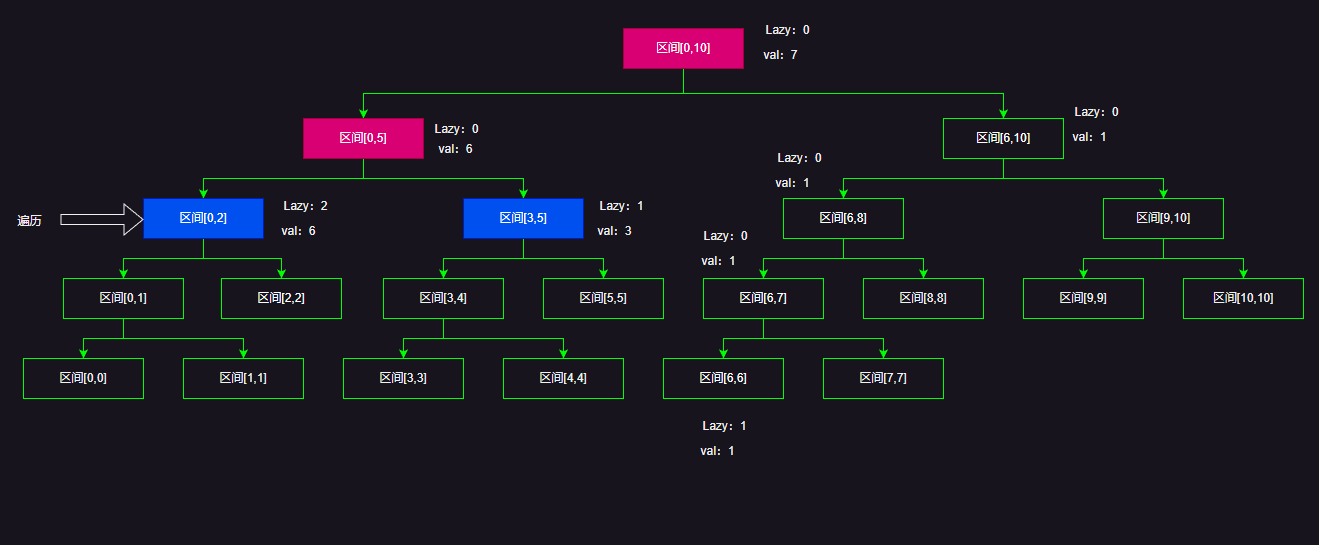
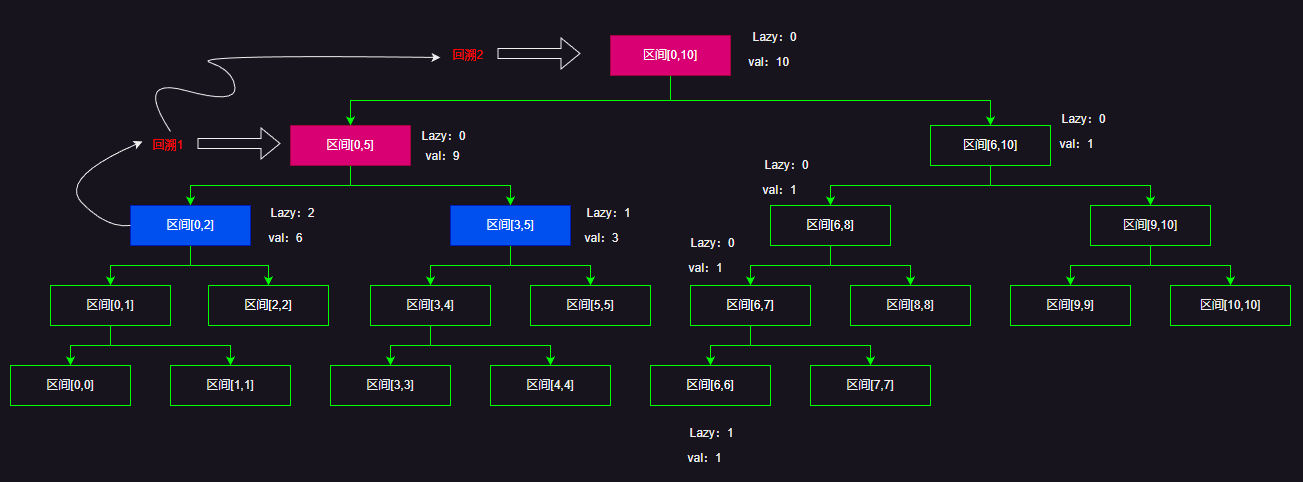
最后别忘了回溯的时候更新父节点的val!
代码
从上面的流程我们可以看出,Lazy标记实际上是一种向下传递,所以我们只需要修改PushDown函数的逻辑既可,那我们就要思考一个问题:何时需要向下传递?
答案很简单:当查询区间不包含当前节点区间的时候,这时候查询的区间一定在当前区间的子节点中,所以需要向下递归,所以在向下递归之前我们需要下传Lazy标记!
这句话需要好好理解一下。
void PushDown(int l, int r, STNode* cur) {if (cur->add == 0) // 如果当前节点没有Lazy标记,则不需要下传直接返回return;int mid = (r - l) / 2 + l;// 将父节点的 Lazy 标记下传到cur->left->add += cur->add;cur->right->add += cur->add;cur->left->val += (mid - l + 1) * cur->add;cur->right->val += (r - mid) * cur->add;cur->add = 0;}
然后相应的Query和Update函数都要做出相应的修改
void Update(int left, int right, int val) {// left right 为要查询的区间 start end 为当前节点所维护的区间 val为区间修改的值function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {if (left <= start && right >= end) {cur->val += (end - start + 1) * val;cur->add += val;return;}// 走到这里代表要查询的区间[left,right]一定在cur节点的子节点中! 一定要理解!!!!!PushDown(start, end, cur);int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {dfs(left, right, mid + 1, end, val, cur->right);}else if (right <= mid) {dfs(left, right, start, mid, val, cur->left);}else {dfs(left, right, mid + 1, end, val, cur->right);dfs(left, right, start, mid, val, cur->left);}PushUp(cur); // 向上更新父节点};dfs(left, right, 0, N, val, root);}int Query(int left, int right) {// left right 为要查询的区间 start end 为当前节点所维护的区间function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, STNode* cur) {if (left <= start && right >= end) {return cur->val;}// 走到这里代表要查询的区间[left,right]一定在cur节点的子节点中! 一定要理解!!!!!PushDown(start, end, cur);int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {ansl = dfs(left, right, mid + 1, end, cur->right);}else if (right <= mid) {ansr = dfs(left, right, start, mid, cur->left);}else {ansl = dfs(left, right, mid + 1, end, cur->right);ansr = dfs(left, right, start, mid, cur->left);}PushUp(cur);return ansl + ansr;};return dfs(left, right, 0, N, root);}
动态开点
到这里实际上线段树就已经结束了,但是做题的时候如果这样搞理论上应该是无法通过的,因为题目的区间都是很大的,一般题目给的区间都是[1,1000000000],如果我们按照上面的构建线段树的方法,内存应该无法通过。与是这里我们又有了一种新的方法——动态开点
我们设想如果我们要查询的区间落在[1,1000000000]上,如果我们上来就开辟1000000000个节点构成线段树,设想下面这种情况,我们的区间查询和更新都集中在[0,5000000000] 上,而区间[500000001,1000000000]只被查询过一次,那么区间[500000001,1000000000]下面500000000个节点实际上是不用开辟的!
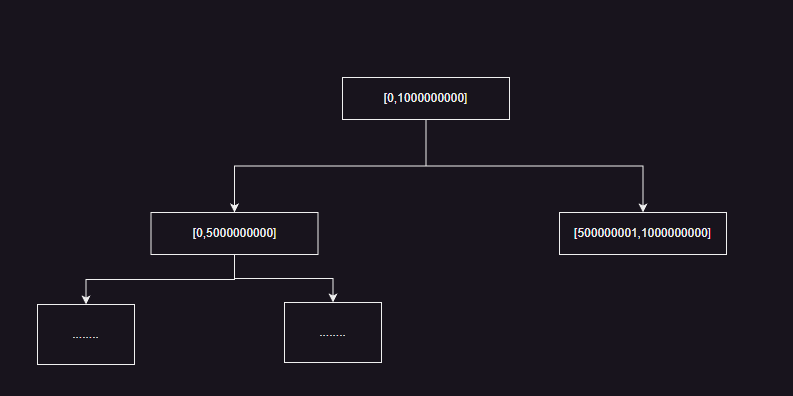
空间上是极大的浪费,我们这里的处理的方法和Lazy标记一样:就是当我们用到该节点的时候,我们再去创建该节点。
而我们何时知道需要访问到子节点?
也就是查询区间不包含当前节点区间的时候,意味着目标节点肯定在子节点中,这时候我们再去开辟子节点
我们把这部分逻辑放在PushDown函数里面去实现。
void PushDown(int l, int r, STNode* cur) {// 创建子节点 如果没有的话if (cur->left == nullptr) cur->left = new STNode{ nullptr,nullptr,0,0 };if (cur->right == nullptr) cur->right = new STNode{ nullptr,nullptr,0,0 };if (cur->add == 0)return;int mid = (r - l) / 2 + l;cur->left->add += cur->add;cur->right->add += cur->add;cur->left->val += (mid - l + 1) * cur->add;cur->right->val += (r - mid) * cur->add;cur->add = 0;}
完整模板
到这里线段树的模板就已经写完了😎
struct STNode {STNode* left;STNode* right;int val = 0;int add;
};class SegmentTree {
public:void PushUp(STNode* cur) {cur->val = cur->left->val + cur->right->val;}SegmentTree() {N = 1000000000;root = new STNode{ nullptr,nullptr,0,0 };}void PushDown(int l, int r, STNode* cur) {if (cur->left == nullptr) cur->left = new STNode{ nullptr,nullptr,0,0 };if (cur->right == nullptr) cur->right = new STNode{ nullptr,nullptr,0,0 };if (cur->add == 0)return;int mid = (r - l) / 2 + l;cur->left->add += cur->add;cur->right->add += cur->add;cur->left->val += (mid - l + 1) * cur->add;cur->right->val += (r - mid) * cur->add;cur->add = 0;}void Update(int left, int right, int val) {// left right 为要查询的区间 start end 为当前节点所维护的区间 val为区间修改的值function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {if (left <= start && right >= end) {cur->val += (end - start + 1) * val;cur->add += val;return;}PushDown(start, end, cur);int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {dfs(left, right, mid + 1, end, val, cur->right);}else if (right <= mid) {dfs(left, right, start, mid, val, cur->left);}else {dfs(left, right, mid + 1, end, val, cur->right);dfs(left, right, start, mid, val, cur->left);}PushUp(cur);};dfs(left, right, 0, N, val, root);}int Query(int left, int right) {// left right 为要查询的区间 start end 为当前节点所维护的区间function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, STNode* cur) {if (left <= start && right >= end) {return cur->val;}PushDown(start, end, cur);int mid = (end - start) / 2 + start;int ansl = 0, ansr = 0;if (left > mid) {ansl = dfs(left, right, mid + 1, end, cur->right);}else if (right <= mid) {ansr = dfs(left, right, start, mid, cur->left);}else {ansl = dfs(left, right, mid + 1, end, cur->right);ansr = dfs(left, right, start, mid, cur->left);}PushUp(cur);return ansl + ansr;};return dfs(left, right, 0, N, root);}private:STNode* root = nullptr; // 根节点int N; // 用于记录线段树查询区间的大小
};
总结
但是在做题的时候还是会对模板进行修改,修改的点主要在区间val的意义上,我们这里模板里面val代表的是区间和,但后面题目里面可能是 区间最大值 、区间最小值…,但是万变不离其宗,线段树的结构是不会变的。
例题:
我的日程安排表 1
我的日程安排表 II
我的日程安排表 III
715. Range 模块
相关文章:

详解线段树
前段时间写过一篇关于树状数组的博客树状数组,今天我们要介绍的是线段树,线段树比树状数组中的应用场景更加的广泛。这些问题也是在leetcode 11月的每日一题频繁遇到的问题,实际上线段树就和红黑树 、堆一样是一类模板,但是标准库…...

C语言——指针的运算
1、指针 - 整数 #include<stdio.h> #define N_VALUES 5 int main() {flout values[N_VALUES];flout *vp;for(vp&values[0];vp<&values[N_VALUES];) //指针的关系运算{*vp0; //指针整数} } 2、指针 - 指针 #include<stdio.h> int main() …...
Apache Hive(部署+SQL+FineBI构建展示)
Hive架构 Hive部署 VMware虚拟机部署 一、在node1节点安装mysql数据库 二、配置Hadoop 三、下载 解压Hive 四、提供mysql Driver驱动 五、配置Hive 六、初始化元数据库 七、启动Hive(Hadoop用户) chown -R hadoop:hadoop apache-hive-3.1.3-bin hive 阿里云部…...

python入门级简易教程
Python是一种高级编程语言,由Guido van Rossum于1991年创建。它是一种通用的、解释型的、高级的、动态的、面向对象的编程语言。 Python的编程哲学是简洁明了,强调代码的可读性和简洁性,使开发人员能够快速开发出正确的代码。Python被广泛用…...

模拟一个集合 里面是设备号和每日的日期
问题: 需要模拟一个集合 里面是设备号和每日的日期 代码如下: static void Main(string[] args){string equipmentCodePar "";DateTime time DateTime.Now; // 获取当前时间DateTime startDate time.AddDays(1 - time.Day);//获取当前月第一…...
antdesign前端一直加载不出来
antdesign前端一直加载不出来 报错:Module “./querystring” does not exist in container. while loading “./querystring” from webpack/container/reference/mf at mf-va_remoteEntry.js:751:11 解决方案:Error: Module “xxx“ does not exist …...
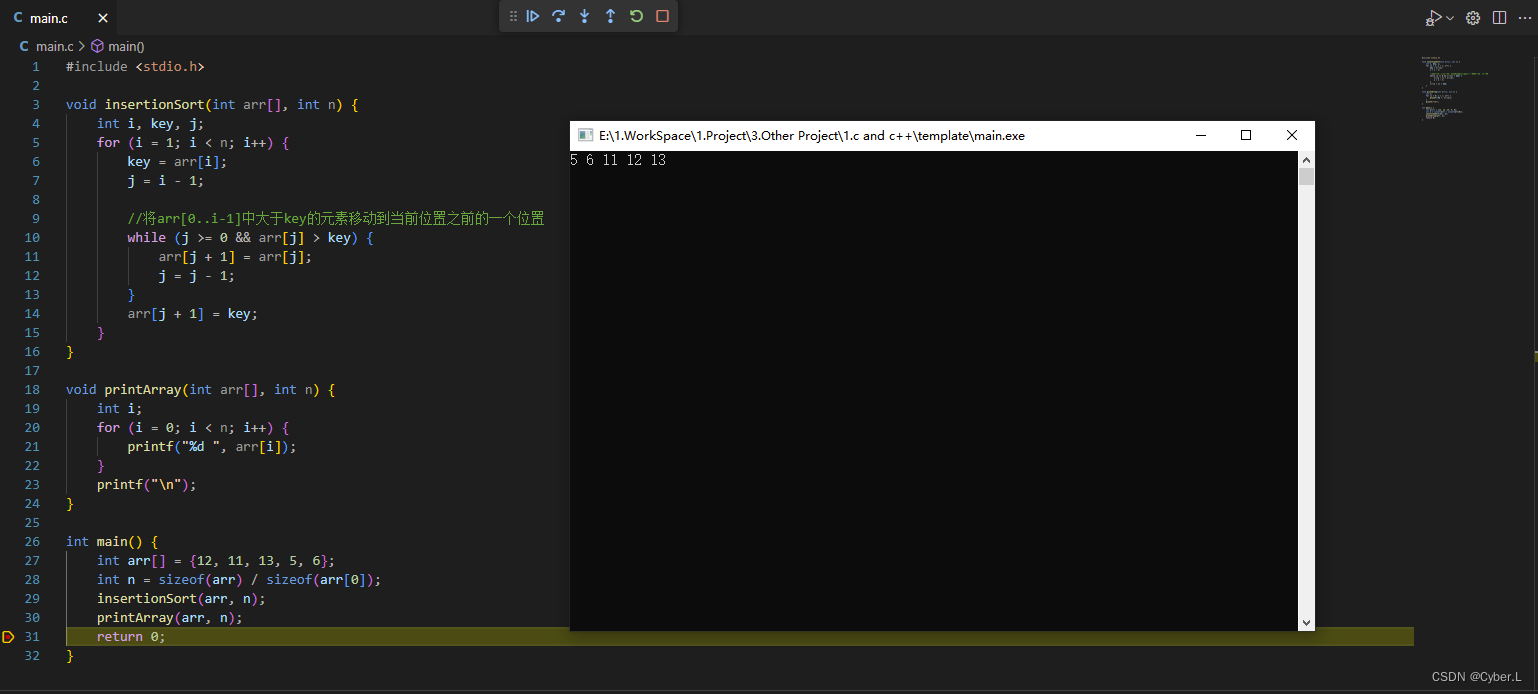
排序算法介绍(一)插入排序
0. 简介 插入排序(Insertion Sort) 是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常…...

2023新优化应用:RIME-CNN-LSTM-Attention超前24步多变量回归预测算法
程序平台:适用于MATLAB 2023版及以上版本。 霜冰优化算法是2023年发表于SCI、中科院二区Top期刊《Neurocomputing》上的新优化算法,现如今还未有RIME优化算法应用文献哦。RIME主要对霜冰的形成过程进行模拟,将其巧妙地应用于算法搜索领域。 …...
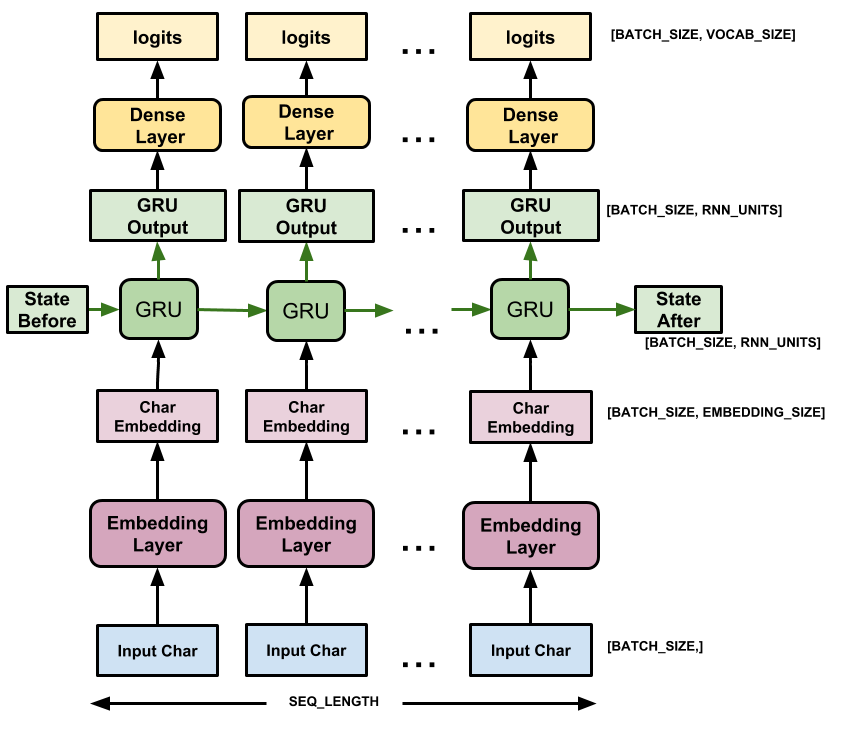
RNN:文本生成
文章目录 一、完整代码二、过程实现2.1 导包2.2 数据准备2.3 字符分词2.4 构建数据集2.5 定义模型2.6 模型训练2.7 模型推理 三、整体总结 采用RNN和unicode分词进行文本生成 一、完整代码 这里我们使用tensorflow实现,代码如下: # 完整代码在这里 imp…...

Rust UI开发(五):iced中如何进行页面布局(pick_list的使用)?(串口调试助手)
注:此文适合于对rust有一些了解的朋友 iced是一个跨平台的GUI库,用于为rust语言程序构建UI界面。 这是一个系列博文,本文是第五篇,前四篇链接: 1、Rust UI开发(一):使用iced构建UI时…...
Linux学习笔记2
web服务器部署: 1.装包: [rootlocalhost ~]# yum -y install httpd 2.配置一个首页: [rootlocalhost ~]# echo i love yy > /var/www/html/index.html 启动服务:[rootlocalhost ~]# systemctl start httpd Ctrl W以空格为界…...

数据结构算法-插入排序算法
引言 玩纸牌 的时候。往往 需要将牌从乱序排列变成有序排列 这就是插入排序 插入排序算法思想 先看图 首先第一个元素 我默认已有序 那我们从第二个元素开始,依次插入到前面已有序的部分中。具体来说,我们将第二个元素与第一个元素比较,…...
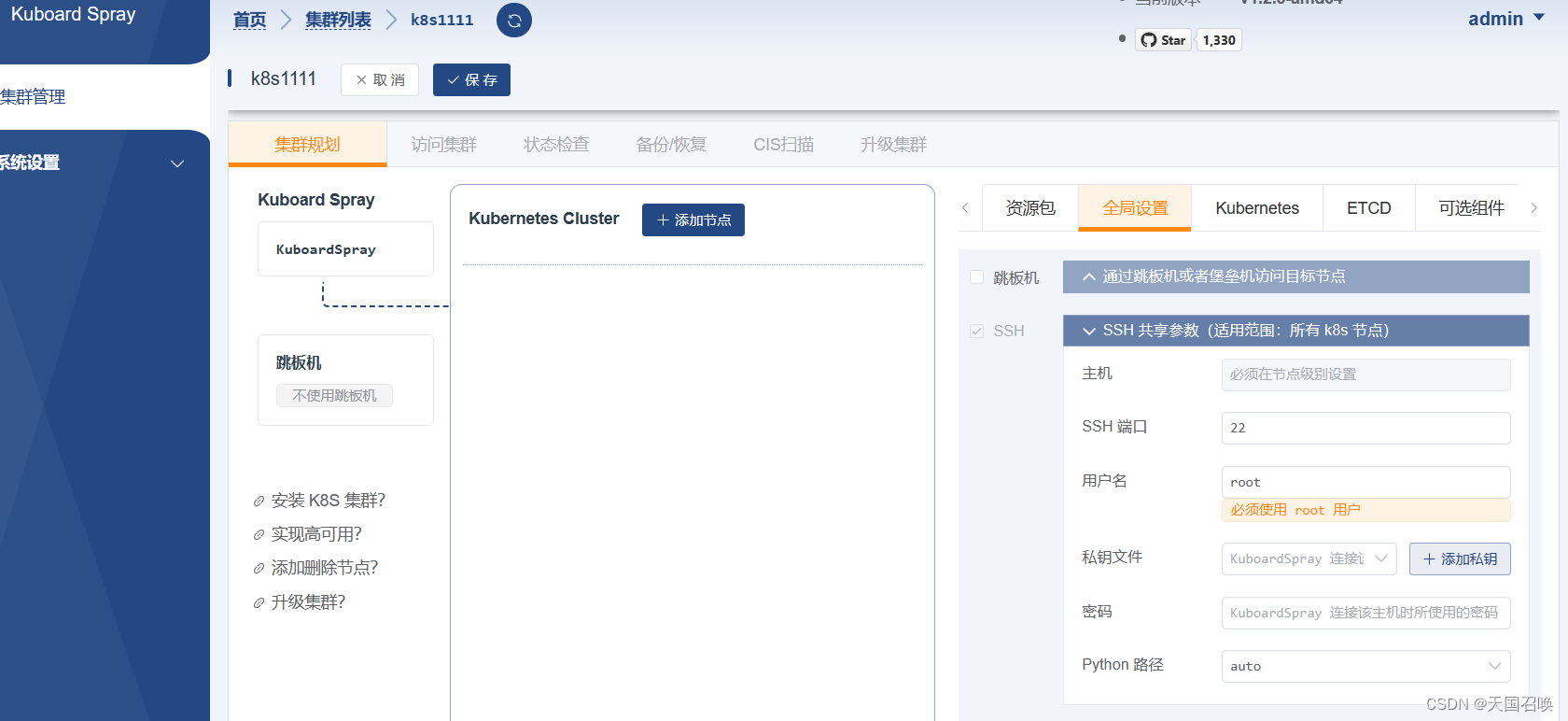
安装Kuboard管理K8S集群
目录 第一章.安装Kuboard管理K8S集群 1.安装kuboard 2.绑定K8S集群,完成信息设定 3.内网安装 第二章.kuboard-spray安装K8S 2.1.先拉镜像下来 2.2.之后打开后,先熟悉功能,注意版本 2.3.打开资源包管理,选择符合自己服务器…...

网络安全行业大模型调研总结
随着人工智能技术的发展,安全行业大模型SecLLM(security Large Language Model)应运而生,可应用于代码漏洞挖掘、安全智能问答、多源情报整合、勒索情报挖掘、安全评估、安全事件研判等场景。 参考: 1、安全行业大模…...
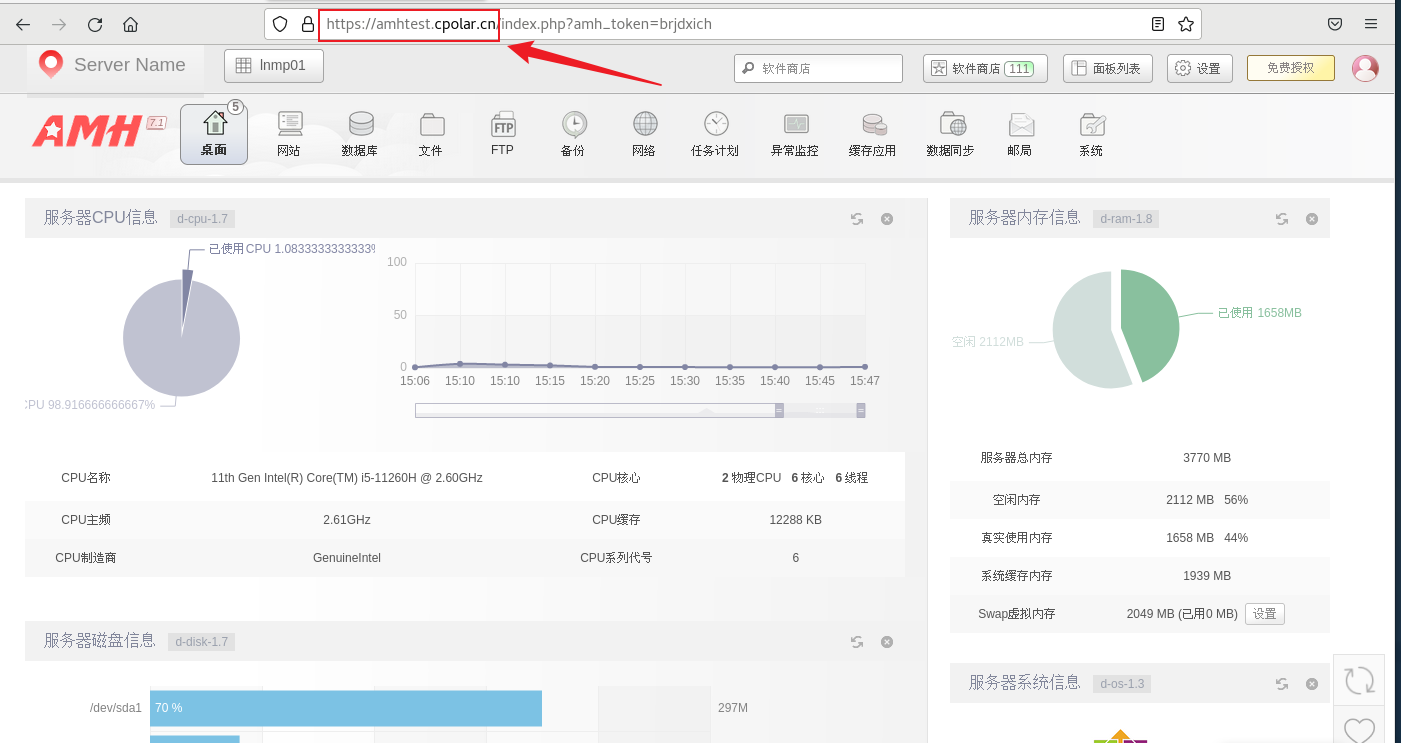
Linux AMH服务器管理面板本地安装与远程访问
最近,我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念,而且内容风趣幽默。我觉得它对大家可能会有所帮助,所以我在此分享。点击这里跳转到网站。 文章目录 1. Linux 安装AMH 面板2. 本地访问AMH 面板3. Linux安装…...

Sharding-Jdbc(3):Sharding-Jdbc分表
1 分表分库 LogicTable 数据分片的逻辑表,对于水平拆分的数据库(表),同一类表的总称。 订单信息表拆分为2张表,分别是t_order_0、t_order_1,他们的逻辑表名为t_order。 ActualTable 在分片的数据库中真实存在的物理表。即上个示例中的t_…...
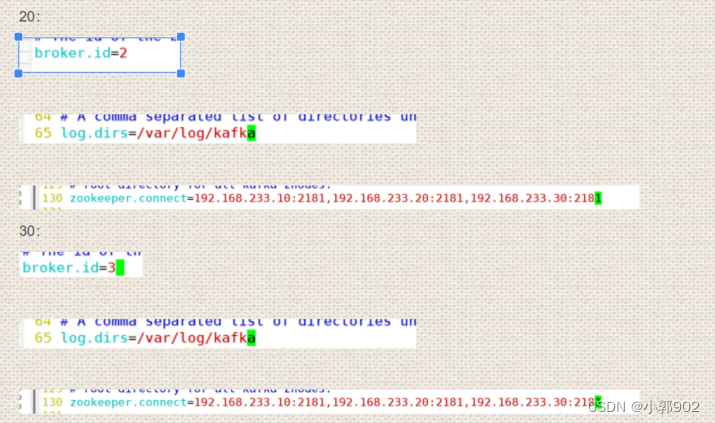
zookeeper集群 +kafka集群
1.zookeeper kafka3.0之前依赖于zookeeper zookeeper是一个开源,分布式的架构,提供协调服务(Apache项目) 基于观察者模式涉及的分布式服务管理架构 存储和管理数据,分布式节点上的服务接受观察者的注册,…...

2022年全国大学生数据分析大赛医药电商销售数据分析求解全过程论文及程序
2022年全国大学生数据分析大赛 医药电商销售数据分析 原题再现: 问题背景 20 世纪 90 年代是电子数据交换时代,中国电子商务开始起步并初见雏形,随后 Web 技术爆炸式成长使电子商务处于蓬勃发展阶段,目前互联网信息碎片化以…...
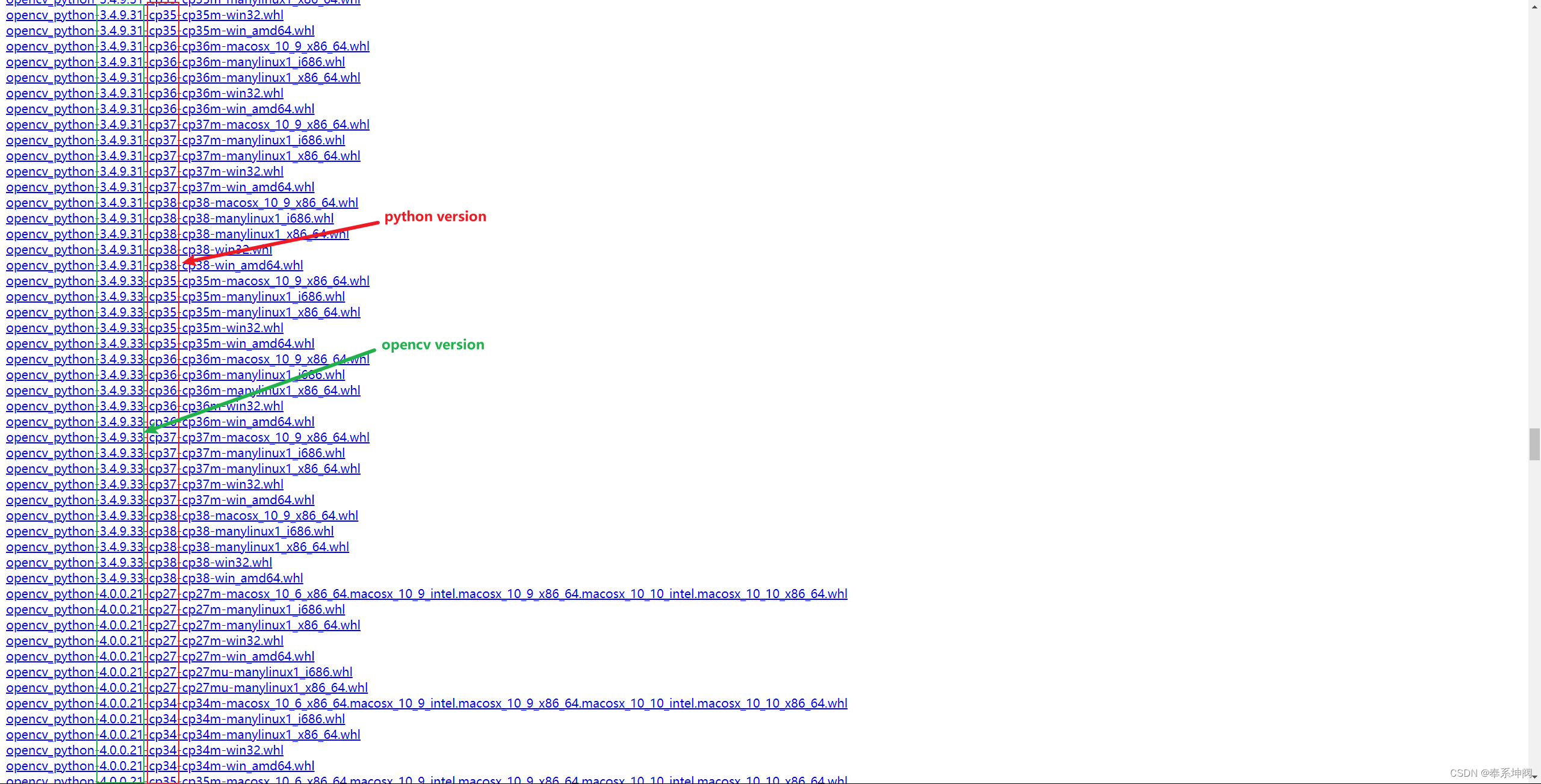
Python版本与opencv版本的对应关系
python版本要和opencv版本相对应,否则安装的时候会报错。 可以到Links for opencv-python上面查看python版本和opencv版本的对应关系,如图,红框内是python版本,绿框内是opencv版本。 查看自己的python版本后,使用下面…...

【开源视频联动物联网平台】LiteFlow
LiteFlow是一个轻量且强大的国产规则引擎框架,可用于复杂的组件化业务的编排领域。它基于规则文件来编排流程,支持xml、json、yml三种规则文件写法方式,再复杂的逻辑过程都能轻易实现。LiteFlow于2020年正式开源,2021年获得开源中…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
