WMMSE方法的使用笔记
标题很帅
- 原论文的描述
- WMMSE的简单应用
无线蜂窝通信系统的预编码设计问题中,经常提到用WMMSE方法设计多用户和速率最大化的预编码,其中最为关键的一步是将原和速率最大化问题转化为均方误差最小化问题,从而将问题由非凸变为关于三个新变量的凸的子问题,交替优化三个子问题即可求解。
对于一般的问题形式,该如何从原和速率最大化问题转化到均方误差最小化问题呢?
原论文的描述
An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel
等待有时间补充
WMMSE的简单应用
原beamforming优化问题
基于上述模型,我们研究了近场多用户通信,考虑当不同用户共享相似方向但距基站距离不同时实现可靠通信的可能性。这里的目的是设计传输波束图案以最大化可实现的总速率,反映每个通道使用可以可靠地传送的总比特数。基于不同的天线架构,对于给定的发射功率约束 P m a x > 0 P_{max} > 0 Pmax>0,感兴趣的任务可以写为:
max { w ~ m } ∑ m = 1 M R m ( { w ~ j } j ∈ M ) s.t. ∑ m = 1 M ∥ w ~ m ∥ 2 ≤ P max , { w ~ m } ∈ W , (14) \begin{array}{l} \max _{\left\{\tilde{\mathbf{w}}_{m}\right\}} \sum_{m=1}^{M} R_{m}\left(\left\{\tilde{\mathbf{w}}_{j}\right\}_{j \in \mathcal{M}}\right) \\ \text { s.t. } \sum_{m=1}^{M}\left\|\tilde{\mathbf{w}}_{m}\right\|^{2} \leq P_{\max }, \quad\left\{\tilde{\mathbf{w}}_{m}\right\} \in \mathcal{W}, \end{array} \tag{14} max{w~m}∑m=1MRm({w~j}j∈M) s.t. ∑m=1M∥w~m∥2≤Pmax,{w~m}∈W,(14)
其中:
R m ( { w ~ j } j ∈ M ) = log 2 ( 1 + ∣ a m H w ~ m ∣ 2 ∑ j ≠ m a m H w ~ j ∣ 2 + σ 2 ) R_{m}\left(\left\{\tilde{\mathbf{w}}_{j}\right\}_{j \in \mathcal{M}}\right)=\log _{2}\left(1+\frac{\left|\mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{m}\right|^{2}}{\left.\sum_{j \neq m} \mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+\sigma^{2}}\right) Rm({w~j}j∈M)=log2 1+∑j=mamHw~j 2+σ2 amHw~m 2
优化问题求解
对于全数字波束聚焦设计,可行的预编码集 W F D \mathcal{W}_{FD} WFD是无约束的,并且包括 C N \mathbb{C}^N CN中 M M M个向量的所有组合。对于单用户情况,即 M = 1 M = 1 M=1,通过设置 w ~ 1 = P max a 1 ∣ a 1 ∣ \tilde{\mathbf{w}}_{1}= \sqrt{P_{\max }} \frac{\mathbf{a}_{1}}{\left|\mathbf{a}_{1}\right|} w~1=Pmax∣a1∣a1来最大化 (14) 中的速率。 。然而,对于 M > 1 M>1 M>1的一般情况,问题(14)是非凸的,因此很难找到最优解。然而,由于(14)与远场操作的干扰广播信道的相应和速率最大化之间的相似性,人们可以利用针对远场系统导出的工具。一种候选策略是使用加权和均方误差(W(S)MMSE)最小化方法[35]来处理问题(14),这保证了收敛到驻点。
通过利用总速率最大化和 MSE 最小化之间的关系 [WMMSE 35,Thm 1],我们有以下引理。
引理 1: W = W F D \mathcal{W} = \mathcal{W}_{FD} W=WFD 的问题 (14) 等价于以下问题(在具有相同全局最优的意义上)
max { w ~ m , u m , v m } ∑ m = 1 M log 2 ( v m ) − v m e m ( u m , { w ~ m } ) s.t. ∑ m = 1 M ∥ w ~ m ∥ 2 ≤ P max , v m ≥ 0 , m ∈ M , (17) \begin{aligned} \max _{\left\{\tilde{\mathbf{w}}_{m}, u_{m}, v_{m}\right\}} & \sum_{m=1}^{M} \log _{2}\left(v_{m}\right)-v_{m} e_{m}\left(u_{m},\left\{\tilde{\mathbf{w}}_{m}\right\}\right) \\ \text { s.t. } & \sum_{m=1}^{M}\left\|\tilde{\mathbf{w}}_{m}\right\|^{2} \leq P_{\max }, \quad v_{m} \geq 0, m \in \mathcal{M}, \end{aligned} \tag{17} {w~m,um,vm}max s.t. m=1∑Mlog2(vm)−vmem(um,{w~m})m=1∑M∥w~m∥2≤Pmax,vm≥0,m∈M,(17)
where u m u_{m} um and v m v_{m} vm are auxiliary variables, and e m ( u m , { w ~ m } ) e_{m}\left(u_{m}\right. , \left.\left\{\tilde{\mathbf{w}}_{m}\right\}\right) em(um,{w~m}) is given by e m ( u m , { w ~ m } ) = ∣ 1 − u m a m H w ~ m ∣ 2 + ∑ j ≠ m ∣ u m a m H w ~ j ∣ 2 + σ 2 ∣ u m ∣ 2 e_{m}\left(u_{m},\left\{\tilde{\mathbf{w}}_{m}\right\}\right)=\left|1-u_{m} \mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{m}\right|^{2}+ \sum_{j \neq m}\left|u_{m} \mathbf{a}_{m}^{H} \tilde{\mathbf{w}}_{j}\right|^{2}+\sigma^{2}\left|u_{m}\right|^{2} em(um,{w~m})= 1−umamHw~m 2+∑j=m umamHw~j 2+σ2∣um∣2 .
虽然问题(17)比问题(14)涉及更多的优化变量,但当其余两组固定时,每组优化变量都是凹的。因此,可以应用块坐标下降法来求解(17),得到总结为算法1的过程,该过程基于[35,Sec.3]中提出的方法。

算法1中,步骤4中的参数λp是与基站发射功率约束相关的拉格朗日乘数。 λp 的选择可以通过超参数优化方案来设置,例如使用二分法[27]、[35]。算法 1 忽略了通信发生在近场的事实,因为该属性仅封装在等效信道向量 {am} 中。尽管如此,正如我们在第四节中以数字方式展示的,这种优化方法以总速率为目标,并没有明确考虑最终的波束图案,它产生聚焦波束,允许多个用户在居住时以最小的交叉干扰共存。相同的角度方向。
相关文章:

WMMSE方法的使用笔记
标题很帅 原论文的描述WMMSE的简单应用 无线蜂窝通信系统的预编码设计问题中,经常提到用WMMSE方法设计多用户和速率最大化的预编码,其中最为关键的一步是将原和速率最大化问题转化为均方误差最小化问题,从而将问题由非凸变为关于三个新变量的…...

MySQL核心知识点整理大全1-笔记
目录 MySQL 一、MySQL的基本概念 1.数据库 2.表 3.列 4.行 5.主键 6.索引 二、MySQL的安装与配置 1.下载MySQL安装包 2.安装MySQL 3.启动MySQL 4.配置MySQL a.设置监听端口和IP地址 b.设置数据存储路径 c.设置字符集和排序规则 5.测试MySQL 三、MySQL的基本操…...
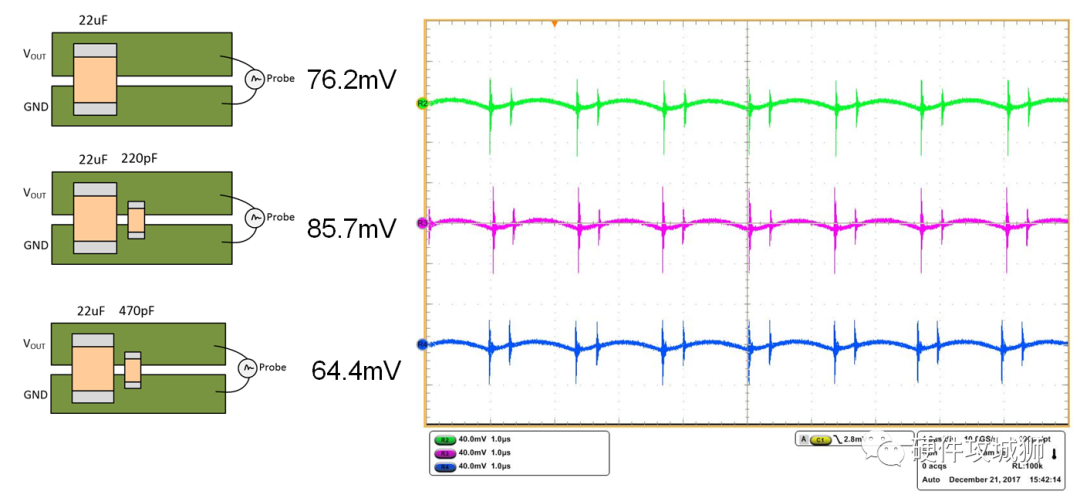
理解输出电压纹波和噪声:来源与抑制
医疗设备、测试测量仪器等很多应用对电源的纹波和噪声极其敏感。理解输出电压纹波和噪声的产生机制以及测量技术是优化改进电路性能的基础。 1:输出电压纹波 以Buck电路为例,由于寄生参数的影响,实际Buck电路的输出电压并非是稳定干净的直流…...
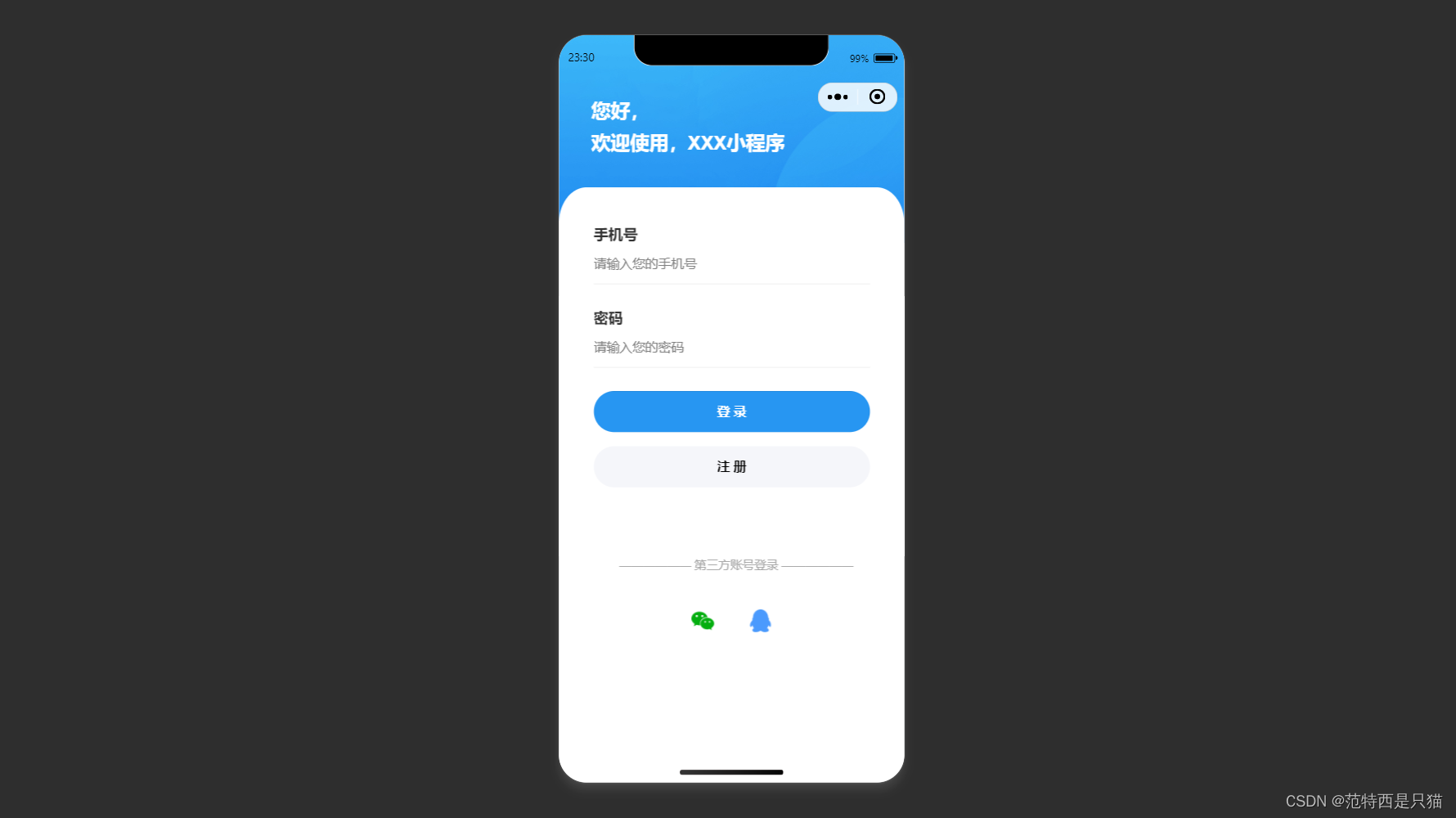
uni-app 微信小程序之好看的ui登录页面(二)
文章目录 1. 页面效果2. 页面样式代码 更多登录ui页面 uni-app 微信小程序之好看的ui登录页面(一) uni-app 微信小程序之好看的ui登录页面(二) uni-app 微信小程序之好看的ui登录页面(三) uni-app 微信小程…...
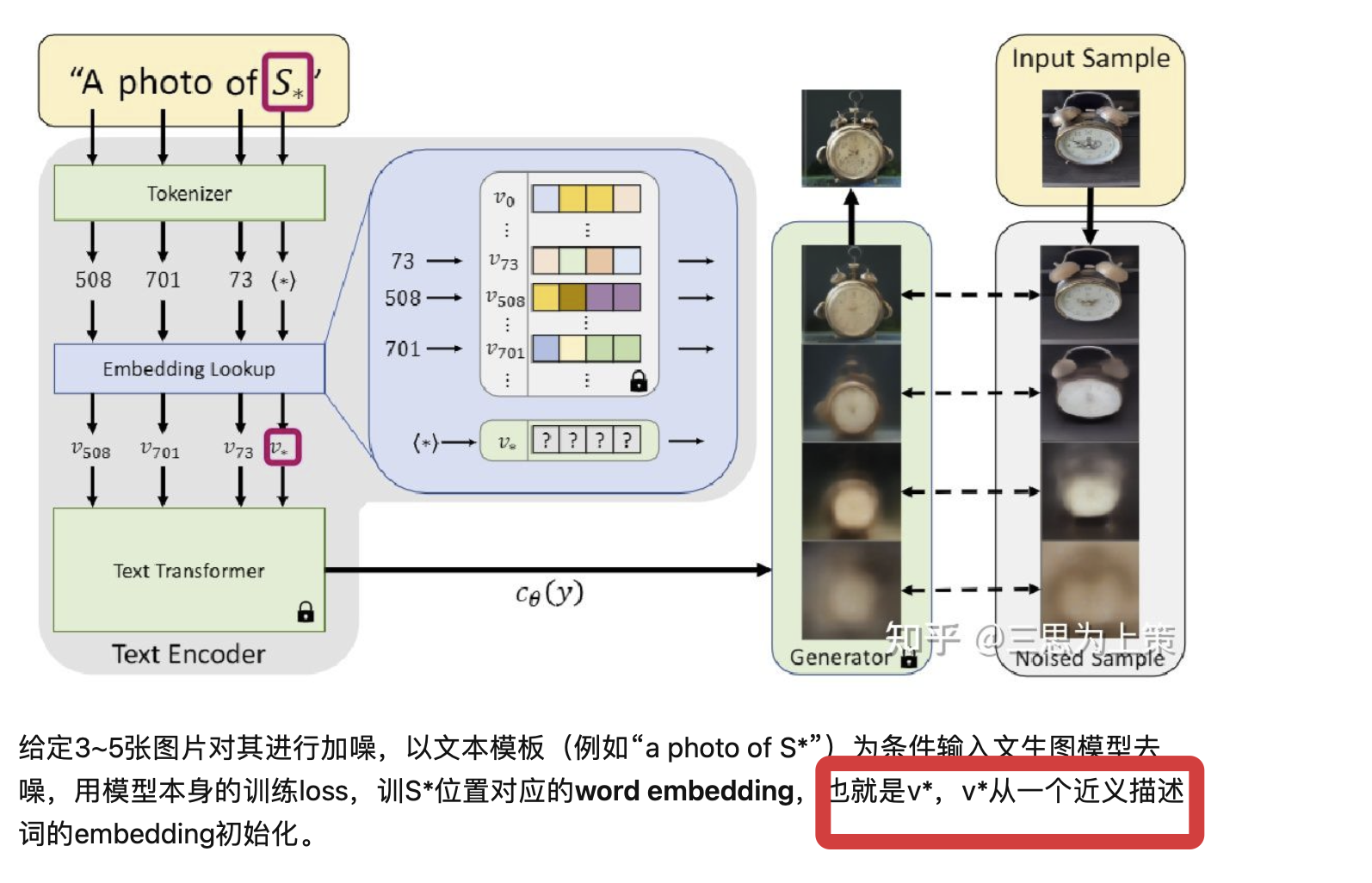
Textual Inversion
参考博客1:https://www.bilibili.com/read/cv25430752/...
)
笙默考试管理系统-MyExamTest----codemirror(47)
笙默考试管理系统-MyExamTest----codemirror(44) 目录 笙默考试管理系统-MyExamTest----codemirror(44) 一、 笙默考试管理系统-MyExamTest----codemirror 二、 笙默考试管理系统-MyExamTest----codemirror 三、 笙默考试…...

JVM中 Minor GC 和 Full GC 的区别
Java中的垃圾回收(Garbage Collection, GC)是自动内存管理的一部分,其主要职责是识别并清除程序中不再使用的对象来释放内存。Java虚拟机(JVM)在运行时进行垃圾回收,主要分为两种类型:Minor GC和…...
二十一章(网络通信)
计算机网络实现了多台计算机间的互联,使得它们彼此之间能够进行数据交流。网络应用程序就是在已连接的不同计算机上运行的程序,这些程序借助于网络协议,相互之间可以交换数据。编写网络应用程序前,首先必须明确所要使用的网络协议…...
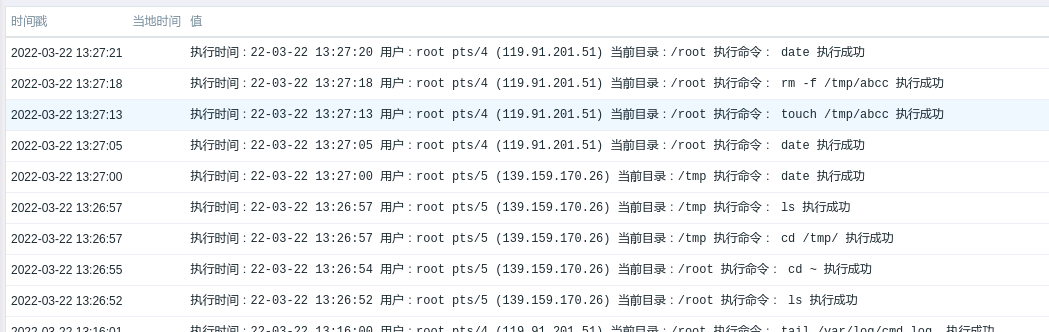
[linux运维] 利用zabbix监控linux高危命令并发送告警(基于Zabbix 6)
之前写过一篇是基于zabbix 5.4的实现文章,但是不太详细,最近已经有两个小伙伴在zabbix 6上操作,发现触发器没有str函数,所以更新一下本文,基于zabbix 6 0x01 来看看效果 高危指令出发问题告警: 发出邮件告…...
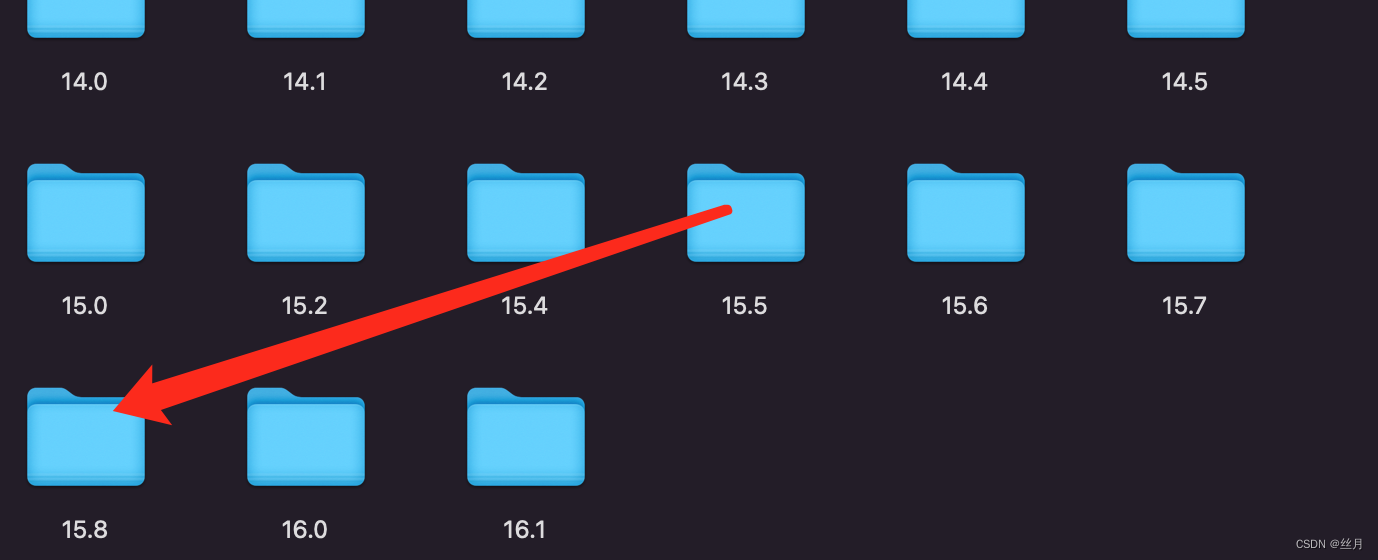
手机升级到iOS15.8后无法在xcode(14.2)上真机调试
之前手机是iOS14.2的系统,在xcode上进行真机测试运行良好,因为想要使用Xcode的Instruments功能,今天将系统更新到了iOS15.8 ,结果崩了 说是Xcode和手机系统不兼容不能进行真机测试。在网上查了好些方法,靠谱的就是下载相关版本的…...

安装TensorFlow2.12.0
文章目录 一、安装Anaconda步骤 1: 下载Anaconda步骤 2: 运行安装程序步骤 3: 选择安装路径步骤 4: 完成安装步骤 5: 启动Anaconda Navigator步骤 6: 创建和管理环境二、安装TensorFlow(一)Anaconda修改国内镜像源(二)安装CPU版TensorFlow2.12.0(三)查看TensorFlow版本…...

elasticsearch 索引数据多了怎么办,如何调优,部署?
当Elasticsearch索引的数据量不断增加时,可以考虑以下调优和部署措施: 增加索引规模:Elasticsearch支持动态增加索引,可以根据数据量的增长情况逐步增加新的索引。同时,也可以考虑使用分片技术,将数据分散…...

人工智能企业引入S-SDLC,推动安全能力大跃升,保障AI技术体系深化落地
某人工智能公司是国际知名的上市企业,核心技术处于世界前沿水平。多年来,该企业在智慧教育、智慧医疗、智慧城市、智慧司法、金融科技、智能汽车、运营商、消费者等领域进行深度技术赋能,深入推进各个行业的智能化、数字化转型建设。 人工智能…...
Docker的数据卷
数据卷 1.数据卷概述 数据卷:容器与宿主机之间数据共享。 数据卷是一个供容器使用的特殊目录,位于容器中。 可将宿主机的目录挂载到数据卷上,对数据卷的修改操作立刻可见,并且更新数据不会影响镜像,从而实现数据在宿…...
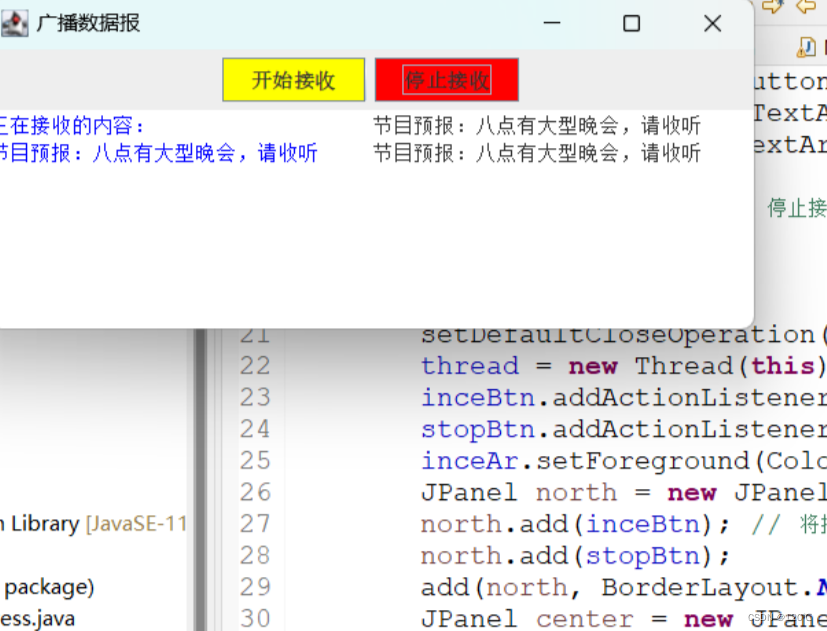
第二十一章总结博客
网络程序设计基础 局域网与互联网 为了实现两台计算机的通信,必须用一个网络线路连接两台计算机。如下图所示 网络协议 1.IP协议 IP是Internet Protocol的简称,是一种网络协议。Internet 网络采用的协议是TCP/IP协议,其全称是Transmission …...
学习php中使用composer下载安装firebase/php-jwt 以及调用方法
学习php中使用composer下载安装firebase/php-jwt 以及调用方法 1、安装firebase/php-jwt2、封装jwt类 1、安装firebase/php-jwt composer require firebase/php-jwt安装好以后出现以下文件: 2、封装jwt类 根据所使用的php框架,在指定目录创建 Token.php <?ph…...

『TypeScript』深入理解变量声明、函数定义、类与接口及泛型
📣读完这篇文章里你能收获到 了解TypeScript变量声明与类型注解掌握TypeScript函数与方法的使用掌握TypeScript类与接口的使用掌握TypeScript泛型的应用 文章目录 一、变量声明与类型注解1. 变量声明2. 类型注解3. 类型推断 二、函数与方法定义1. 函数定义2. 方法定…...
如何优雅使用 vue-html2pdf 插件生成pdf报表
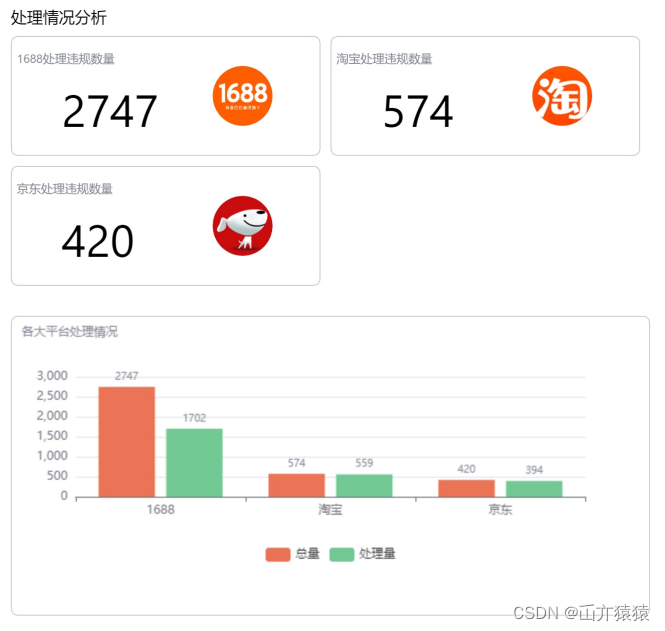
使用 vue-html2pdf 插件 业务背景,老板想要一份能征服客户的pdf报表,传统的pdf要手撕,企业中确实有点耗费时间,于是github上面看到开源的这个插件就…废话不多说,直接上教程 1.使用下面命令安装 vue-html2pdf npm i…...
C语言第十六集(前)
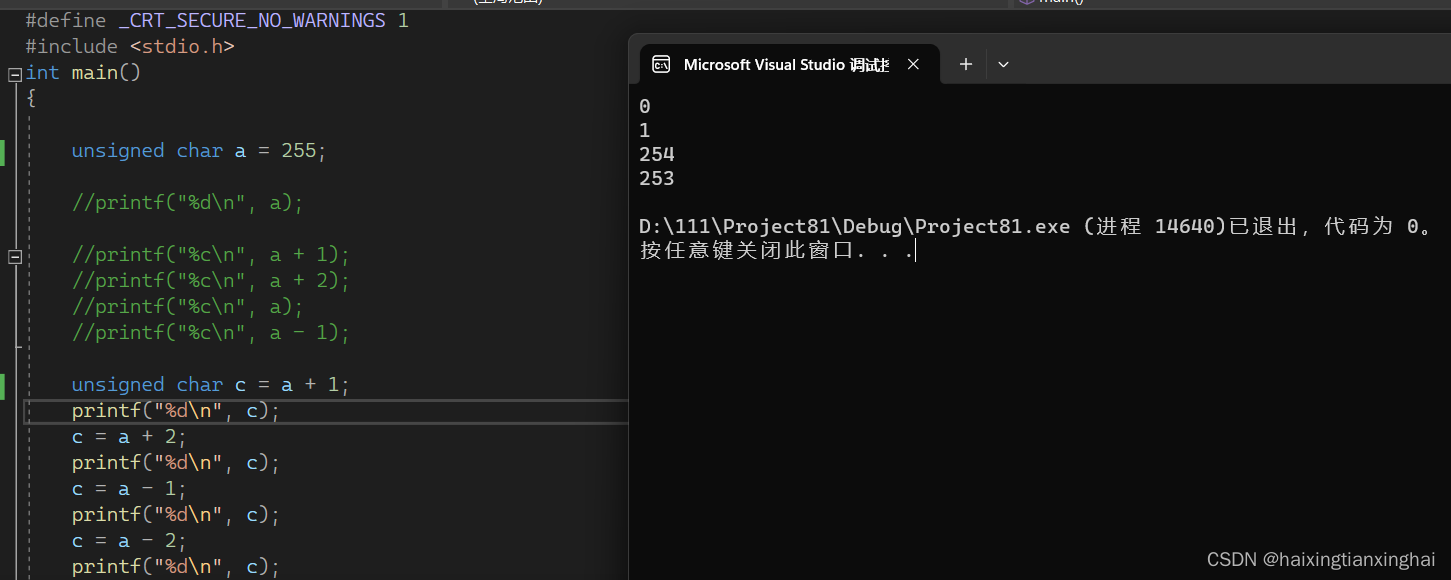
1.关于那个整形存储入char的 是先取好补码,再截断 例: 2.%u是以十进制的形式打印无符号整数 3.注意(背):存储的char类型变量的补码为10000000的直接解析为-128 4.signed char 类型的变量取值范围是-128~127 5.unsigned char 类型的变量取值范围是0~255 6.有符号类型的变量…...
Makefile语法
一、Makefile规则格式 Makefile 里面是由一系列的规则组成的,这些规则格式如下: 目标…... : 依赖文件集合…… 命令 1 命令 2 ……参考上一节gcc编译器与Makefile入门参考这条规则 1 main: main.o input.o calcu.o2 gcc -o main main.o input.o c…...

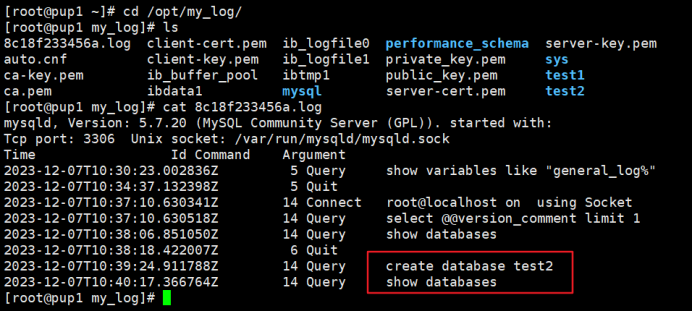
在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...
