第二证券:十字星买入法?
首要,让我们了解一下什么是十字星。十字星是指股票图表上出现的一种形状,它位于较长的蜡烛线的中心,上下为两个小蜡烛线。这种形状通常被解释为股票价格或许会反转的信号,由于它表明晰股价在一段时间内处于相对稳定的水平。当股价上涨并构成一个十字星时,它或许预示着进一步的上涨。相反,当股价跌落并构成一个十字星时,它或许意味着股市会持续跌落。
尽管股票图表剖析是出资抉择方案的一种重要东西,可是,它的猜测才能仍有限。股票商场是极点杂乱和不稳定的,它由各种因素影响,例如公司基本面、经济事情、政治动乱、自然灾害以及商场心情等。股价不坚定的原因不尽相同,因而把十字星形状作为不必考虑和判别的独立战略是不合适的。假如这种形状真的很牢靠,那么股票商场定价办法根本不会存在科技进步、自然灾害、公司财报发布等事情的不坚定。
其次,十字星买入法被广泛推广和误导。在互联网上,你可以找到数不清的有关十字星买入法的文章、视频和博客,它们宣称这种战略十分成功,可以协助你获得很多收益。这些文章很少提示你,乃至完全忽略了商场风险以及股票价格涨跌的无法猜测性。更严峻的是,它们或许触及诈骗行为,让你购买贵重的炒股训练课程或交易平台。
最终,股票商场需求出资者做出理性的、基于全面信息的抉择方案。股票商场不是大家学过的数学标题,而是这个世界上最杂乱的范畴之一。它需求出资者对金融、会计和管理知识有深入的了解,需求出资者耐性和恒心的投入。假如你是新手,不要盲目寻求捷径。首要应该向专业人士咨询,学习怎样剖析公司的基本面、了解股票商场的运作规则。
总之,以十字星形状作为买卖股票的信号,或许有其价值和使用场景,但绝不是一个牢靠的、简单的买入战略。要更好地出资股票,我们需求更多地学习和考虑,理性地抉择方案。
相关文章:

第二证券:十字星买入法?
首要,让我们了解一下什么是十字星。十字星是指股票图表上出现的一种形状,它位于较长的蜡烛线的中心,上下为两个小蜡烛线。这种形状通常被解释为股票价格或许会反转的信号,由于它表明晰股价在一段时间内处于相对稳定的水平。当股价…...
【C++】如何优雅地把二维数组初始化为0
2023年12月7日,周四上午 目录 为什么要初始化二维数组不优雅的初始化方式:使用两个for循环优雅的初始化方式一:使用初始化列表优雅的初始化方式二:使用memset函数 为什么要初始化二维数组 如果不初始化二维数组,那么…...

8 个顶级的 PDF 转 Word 转换器
PDF 是跨不同平台分发信息而不影响内容格式的好方法。但这种安全级别确实有其缺点。没有直接的方法来编辑 PDF 上的文本或内容。编辑 PDF 文档的唯一方法是将其转换为 Word 文档或其他可以编辑的文件类型。将 PDF 转换为 Word 是根据需要编辑 PDF 内容的最快方法。有许多免费的…...

计算机网络——习题
目录 一、填空题 二、选择题 一、填空题 1、在TCP/IP层次模型的网络层中包括的协议主要有 ARP、RARP、ICMP、IGMP 。 2、传输层的传输服务有两大类: 面向连接(TCP)和 无连接服务(UDP)。 3、Internet所提供的三项…...
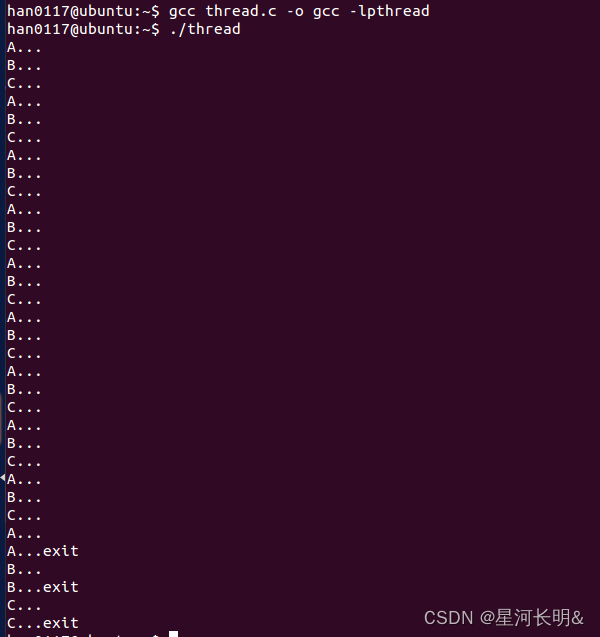
Linux 线程——信号量
题目:编写代码实现编写一个程序,开启三个线程,这三个线程的ID分别是A,B,C,每个线程将自己的ID在屏幕上打印10遍,要求输出必须按照ABC的顺序显示,如:ABCABCABC... 思路:创建三个ID分别为ABC的线程…...

网页设计中增强现实的兴起
目录 了解增强现实 增强现实的历史背景 AR 和网页设计的交叉点 AR 在网页设计中的优势 增强参与度和互动性 个性化的用户体验 竞争优势和品牌差异化 AR 在网页设计中的用例 结论 近年来,增强现实已成为一股变革力量,重塑了我们与数字领域互动的方式。它被…...

Android7.0新特性
OverView模式 多窗口模式,大屏幕设备可以打开两个应用程序窗口 Data Saver 流量保护机制。启用该模式,系统将拦截后台数据使用,在适当的情况下减少前台应用使用的数据量,通过配置厂商白名单可以让应用免受该模式的影响。谷歌也…...

visual studio 2022中使用vcpkg包管理器
安装步骤 1、拷贝vcpkg $ git clone https://hub.njuu.cf/microsoft/vcpkg.git $ .\vcpkg\bootstrap-vcpkg.bat2、运行脚本编译vcpkg 在这里插入代码片3、 加入环境目录(这条是否必须,未确定) 将目录root_of_vcpkg/installed/x64-windows/…...

C语言-链表_基础
链表-基础 1. 数组 1.1 静态数组 例子:int nums[5] {0};struct person ps[5]; 缺点:1,无法修改地址2,无法动态定义长度3,占用内存过大或过小4,增删速度慢 优点数组的内存是连续开辟的,所以读取速度快1.2 动态数组 例子:int *nums (int *) calloc(5,sizeof(int));struct p…...

Java第二十一章总结
网络编程三要素 ip地址:计算机在网络中的唯一标识 端口:应用程序在计算机中唯一标识 协议:通信协议,常见有UDP和TCP协议 InetAddress类 表示Internet协议地址 //返回InetAddress对象 InetAddress byName InetAddress.…...

【keil备忘录】2. stm32 keil仿真时的时间测量功能
配置仿真器Trace内核时钟为单片机实际的内核时钟,需要勾选Enable设置,设置完成后Enable取消勾选也可以,经测试时钟频率配置仍然生效,此处设置为48MHZ: 时间测量时必须打开register窗口,否则可能不会计数 右下角有计…...

图的存储(邻接矩阵,边集数组,邻接表,链式前向星)
目录 🌼图的存储 (1)邻接矩阵 (2)边集数组 (3)邻接表 (4)链式前向星 😀刷题 🐍最大节点 🐍有向图 D 和 E 🐍奶牛…...
)
Linux 基础知识整理(二)
Linux系统目录结构 Linux采用的是树型结构。最上层是根目录,其他的所有目录都是从根目录出发而生成的。微软的DOS和windows也是采用树型结构,但是在DOS和 windows中这样的树型结构的根是磁盘分区的盘符,有几个分区就有几个树型结构ÿ…...

2024年值得关注的8个未来数据库
2024年值得关注的8个未来数据库 关系型数据库管理系统在数据库技术领域占据主导地位已经多年了。当SQL在1970年代首次出现时,关系型数据库管理系统的使用和受欢迎程度迅速提升。很快,MySQL成为了大多数公司和团队首选的数据库。 然而,2023年…...
C++新经典模板与泛型编程:将trait类模板用作模板参数
将trait类模板用作模板参数 template<typename T> struct SumFixedTraits;template<> struct SumFixedTraits<char> {using sumT int;static sumT initValue() {return 0;} };template<> struct SumFixedTraits<int> {using sumT __int64;sta…...

BUUCTF-[GYCTF2020]FlaskApp flask爆破pin
这道题不需要爆破也可以getshell ssti都给你了 {{((lipsum.__globals__.__builtins__[__import__](so[::-1])[popen]("\x63\x61\x74\x20\x2f\x74\x68\x69\x73\x5f\x69\x73\x5f\x74\x68\x65\x5f\x66\x6c\x61\x67\x2e\x74\x78\x74")).read())}} 但是学习记录一下pin…...

web前端实现LED功能、液晶显示时间、数字
MENU 效果演示html部分JavaScript部分css部分 效果演示 html部分 <div id"app"><!-- 页面 --><div class"time-box"><!-- 时 --><div class"house-box"><bit-component :num"houseTem"></bit…...

YOLOv8改进 | 2023 | DiverseBranchBlock多元分支模块(有效涨点)
一、本文介绍 本文带来的改进机制是YOLOv8模型与多元分支模块(Diverse Branch Block)的结合,Diverse Branch Block (DBB) 是一种用于增强卷积神经网络性能的结构重新参数化技术。这种技术的核心在于结合多样化的分支,这些分支具有…...
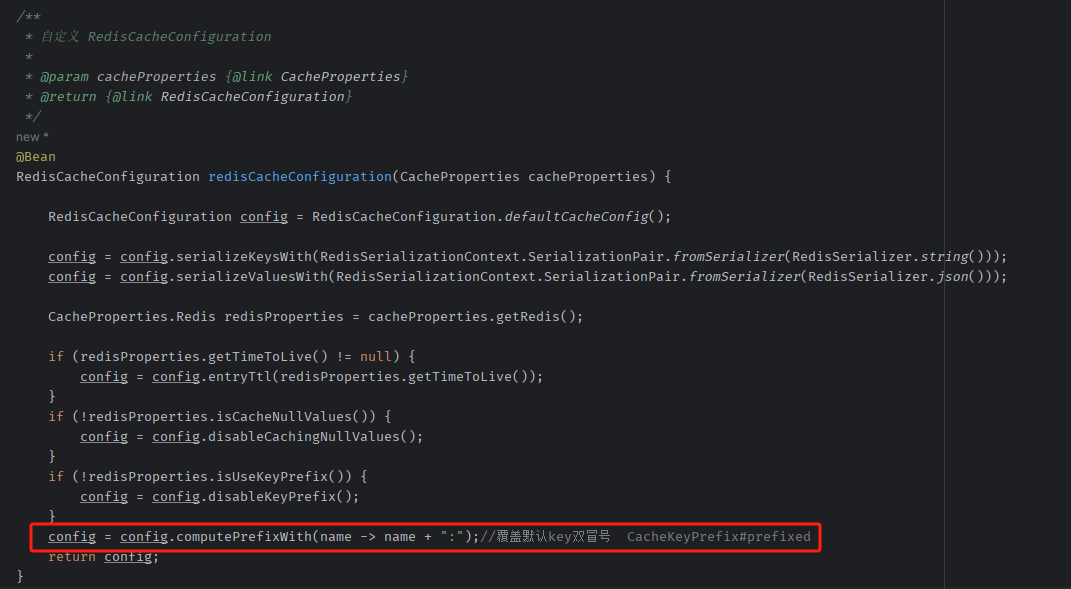
Spring Boot 3 整合 Spring Cache 与 Redis 缓存实战
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

kubeadm 安装k8s1.28.x 底层走containerd 容器
1. k8s1.28.x 的概述 1.1 k8s 1.28.x 更新 Kubernetes v1.28 是 2023 年的第二个大版本更新,包含了 46 项主要的更新。 而今年发布的第一个版本 v1.27 有近 60 项,所以可以看出来,在发布节奏调整后, 每个 Kubernetes 版本中都会包…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
