AcWing算法提高课-3.1.3香甜的黄油
宣传一下算法提高课整理 <—
CSDN个人主页:更好的阅读体验 <—

题目传送门点这里
题目描述
农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖。
把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。
当然,他将付出额外的费用在奶牛上。
农夫John很狡猾,就像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。
他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。
给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
数据保证至少存在一个牧场和所有牛所在的牧场连通。
输入格式
第一行: 三个数:奶牛数 N,牧场数 P,牧场间道路数 C。
第二行到第 N+1 行: 1 到 N 头奶牛所在的牧场号。
第 N+2 行到第 N+C+1 行:每行有三个数:相连的牧场A、B,两牧场间距 D,当然,连接是双向的。
输出格式
共一行,输出奶牛必须行走的最小的距离和。
数据范围
1≤N≤500,1≤N≤500,1≤N≤500,
2≤P≤800,2≤P≤800,2≤P≤800,
1≤C≤1450,1≤C≤1450,1≤C≤1450,
1≤D≤2551≤D≤2551≤D≤255
样例输入
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5
样例输出
8
思路
本题可以先枚举黄油的位置,再用 spfa 求出每个牧场到当前位置的最短路。
-
这道题不是每个牧场一个奶牛,一个牧场可能有好几个奶牛
-
于是,我们用 cntcntcnt 数组来存第 iii 个仓库有几个奶牛
-
第 iii 个牧场的奶牛路程就是 di×cntid_i×cnt_idi×cnti
····························································································
-
题目中说:数据保证至少存在一个牧场和所有牛所在的牧场连通
-
但是,没有奶牛的牧场虽然有可能贡献答案,也有可能不与有奶牛的牧场连通
-
所以枚举起点时要注意牧场之间的连通性
算法时间复杂度
复杂度为 O(nm)O(nm)O(nm),可以过
本题使用STL中的queue时间上会慢一点,不过不影响AC
这里贴上提交记录:
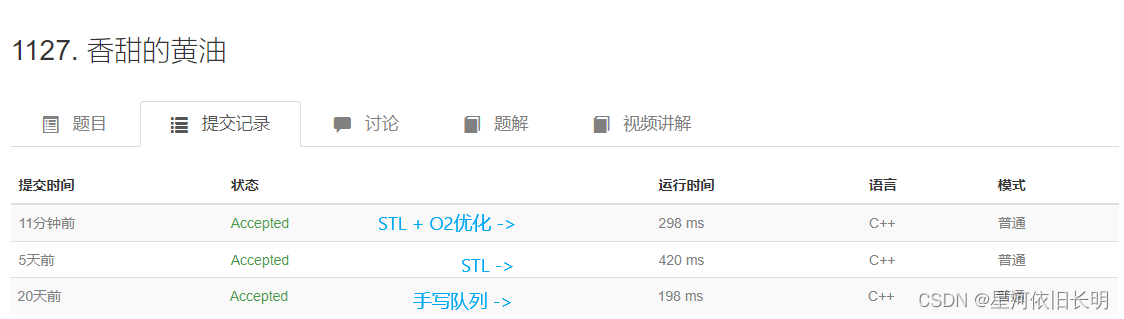
可以看到,queue即使加了O2,效率也比不上手写队列。
所以考试能手写就别用STL,除非你的时间限制很充裕。
AC Code
C++C++C++
#include <iostream>
#include <cstring>using namespace std;typedef pair<int, int> PII;const int N = 810, M = 3010;
const int INF = 0x3f3f3f3f;int n, m, p;
int id[N];
int h[N], e[M], w[M], ne[M], idx;
int q[N], dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}int spfa(int S)
{memset(dist, 0x3f, sizeof(dist));dist[S] = 0;int hh = 0, tt = 1;q[0] = S, st[S] = 1;while (hh != tt){int t = q[hh ++ ];if (hh == N) hh = 0;st[t] = 0;for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];if (!st[j]){q[tt ++ ] = j;if (tt == N) tt = 0;st[j] = 1;}}}}int res = 0;for (int i = 0; i < n; i ++ ){int j = id[i];if (dist[j] == INF) return INF;res += dist[j];}return res;
}int main()
{memset(h, -1, sizeof h);scanf("%d%d%d", &n, &p, &m);for (int i = 0; i < n; i ++ )scanf("%d", &id[i]);for (int i = 0; i < m; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);}int res = INF;for (int i = 1; i <= p; i ++ )res = min(res, spfa(i));printf("%d\n", res);return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-3.1.3香甜的黄油
宣传一下算法提高课整理 <— CSDN个人主页:更好的阅读体验 <— 题目传送门点这里 题目描述 农夫John发现了做出全威斯康辛州最甜的黄油的方法:糖。 把糖放在一片牧场上,他知道 N 只奶牛会过来舔它,这样就能做出能卖好价…...

私库搭建1:Nexus 安装 Docker 版
本文内容以语雀为准 文档 https://hub.docker.com/r/sonatype/nexus3Docker 安装:https://www.yuque.com/xuxiaowei-com-cn/gitlab-k8s/docker-install 安装 创建文件夹 由于 Nexus 的数据可能会很大,比如:作为 Docker、Maven 私库时&…...

LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】
LeetCode-面试题 05.02. 二进制数转字符串【数学,字符串,位运算】题目描述:解题思路一:简单暴力。小数点后面的二进制,now首先从0.5开始之和每次除以2。然后依次判断当前数是否大于now,是则答案加1。若等于…...
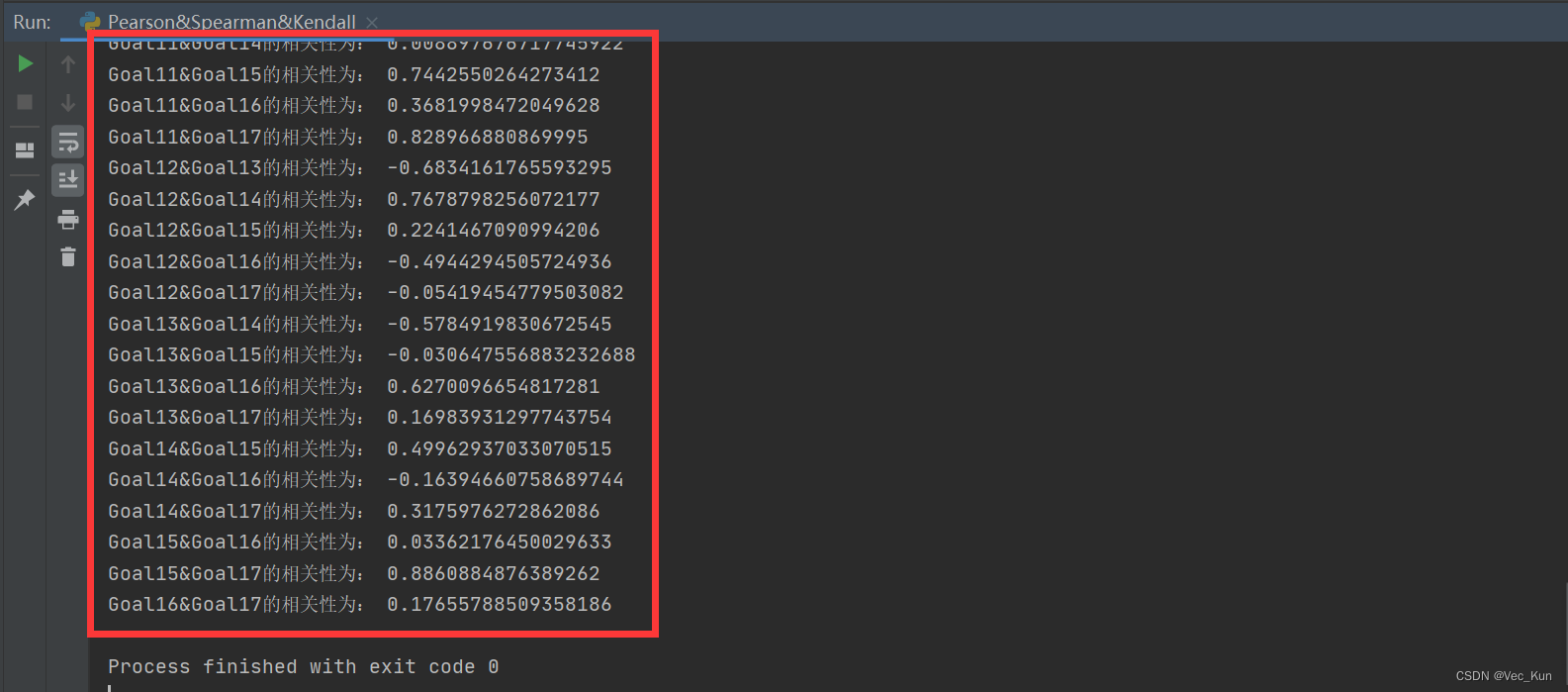
pandas: 三种算法实现递归分析Excel中各列相关性
目录 前言 目的 思路 代码实现 1. 循环遍历整个SDGs列,两两拿到数据 2. 调用pandas库函数直接进行分析 完整源码 运行效果 总结 前言 博主之前刚刚被学弟邀请参与了2023美赛,这也是第一次正式接触数学建模竞赛,现在已经提交等待结果…...

【Python百日进阶-Web开发-Vue3】Day543 - Vue3 商城后台 03:登录页面初建
文章目录 一、创建登录页面 login.vue二、登录页面响应式处理,以适应不同大小的屏幕2.1 element-plus 的layout布局中关于响应式的说明2.2 修改login.vue文件2.2.1 :lg=16 大于1200px 横排 2:12.2.2 :md=12 大于992小于1200px 横排 1:12.2.3 小于992 竖排三、引入Element-plus…...
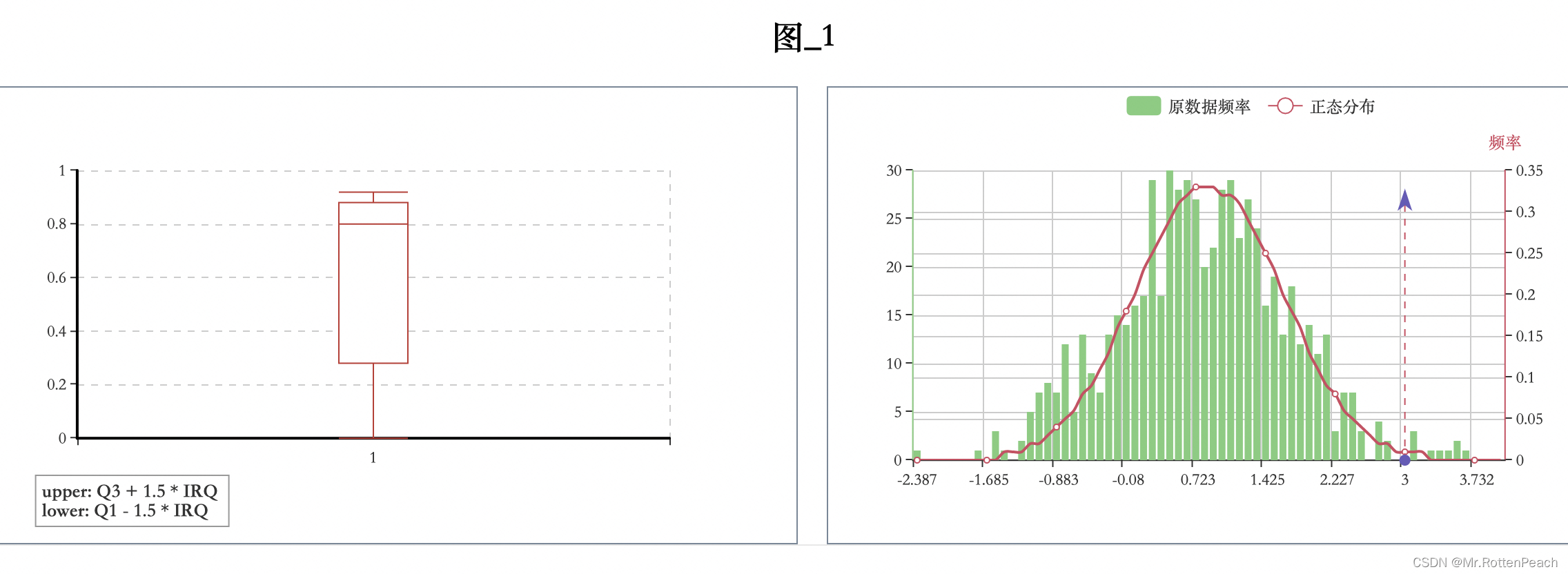
python画直方图,刻画数据分布
先展示效果 准备一维数据 n 个数据元素计算最大值,最小值、均值、标准差、以及直方图分组 import numpy as np data list() for i in range(640):data.append(np.random.normal(1)) print(data)z np.histogram(data, bins64) print(list(z[0])) ### 对应 x 轴数据…...
【学数学关键是要学会在什么情况下,知道使用什么工具。】)
几何学小课堂:非欧几何(广义相对论采用黎曼几何作为数学工具)【学数学关键是要学会在什么情况下,知道使用什么工具。】
文章目录 引言I 非欧几何1.1 黎曼几何1.2 共形几何1.3 罗氏几何II 黎曼几何的应用2.1 广义相对论2.2 超弦III 理解不同的几何体系的共存3.1 更扎实的欧氏几何3.2 殊途同归引言 公理有错会得到两种情况: 如果某一条自己设定的新公理和现有的公理相矛盾,那么相应的知识体系就建…...

Ubuntu配置静态IP的方法
Ubuntu配置静态IP的方法前言一、查看虚机分配的网卡IP二、查看网卡的网关IP三、配置静态IP1.配置IPv4地址2.执行netplan apply使改动生效3.配置的网卡未生效,修改50-cloud-init.yaml文件解决4.测试vlan网络通信总结前言 Ubuntu18.04 欧拉环境 vlan网络支持ipv6场景…...

90%的人都不算会爬虫,这才是真正的技术,从0到高手的进阶
很多人以为学会了urlib模块和xpath等几个解析库,学了Selenium就会算精通爬虫了,但到外面想靠爬虫技术接点私活,才发现寸步难行。 龙叔我做了近20年的程序员,今天就告诉你,真正的爬虫高手应该学哪些东西,就…...

排序之损失函数List-wise loss(系列3)
排序系列篇: 排序之指标集锦(系列1)原创 排序之损失函数pair-wise loss(系列2)排序之损失函数List-wise loss(系列3) 最早的关于list-wise的文章发表在Learning to Rank: From Pairwise Approach to Listwise Approach中,后面陆陆续续出了各种变形&#…...

js对象和原型、原型链的关系
JS的原型、原型链一直是比较难理解的内容,不少初学者甚至有一定经验的老鸟都不一定能完全说清楚,更多的"很可能"是一知半解,而这部分内容又是JS的核心内容,想要技术进阶的话肯定不能对这个概念一知半解,碰到…...
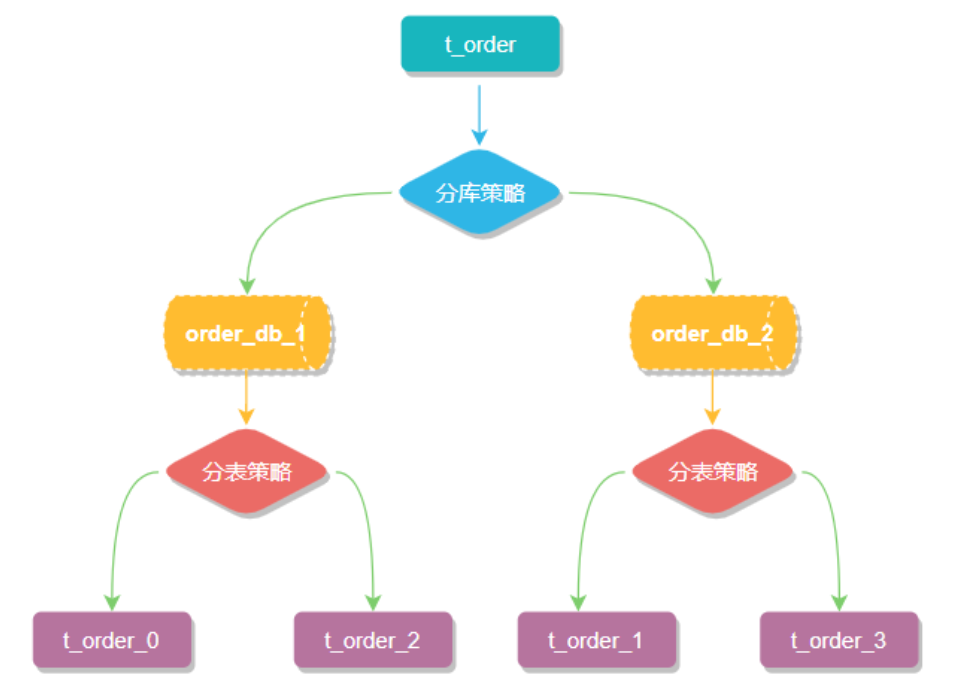
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表
【SpringBoot高级篇】SpringBoot集成Sharding-JDBC分库分表Apache ShardingSphere分库分表分库分表的方式垂直切分垂直分表垂直分库水平切分水平分库水平分表分库分表带来的问题分库分表中间件Sharding-JDBCsharding-jdbc实现水平分表sharding-jdbc实现水平分库sharding-jdbc实…...

Shell特殊字符
shell语言,一些字符是有特殊意义的。 根据作用分为几种特殊符号 一、空白 shell调用函数,不像c语言那样用把参数放到括号里,用逗号分隔。而是用空格作为参数之间,参数与函数名之间的分隔符。 换行符也是特殊字符。换行符用作一条命…...

【计算机二级python】综合题目
计算机二级python真题 文章目录计算机二级python真题一、德国工业战略规划二、德国工业战略规划 第一问三、德国工业战略规划 第二问一、德国工业战略规划 描述:在右侧答题模板中修改代码,删除代码中的横线,填写代码,完成考试答案。…...

字节直播leader面
设计评论系统(缓存怎么做) mysql是否有主从延迟,如何解决 mysql有主从延迟 主从延迟主要因为mysql主从同步的机制,mysql有三种同步机制 同步复制:事务线程等待所有从库复制成功响应异步复制:事务不等待…...

PIC 单片机的时钟
注意:本文的内容无法保证绝对精确,后续可能会做改动,只是自己的笔记。这里的资料均源自数据手册本身。PIC18系列单片机的参考时钟可以选择三个基础时钟源:Primary Clock, OSC1 or OSC2,Secondary Clock,Inner clock.时钟源分为两个…...
【数据结构】关于二叉树你所应该知道的数学秘密
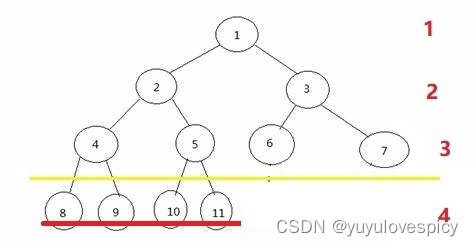
目录 1.什么是二叉树(可以跳过 目录跳转) 2.特殊的二叉树(满二叉树/完全二叉树) 2.1 基础知识 2.2 满二叉树 2.3 完全二叉树 3.二叉树的数学奥秘(主体) 3.1 高度与节点个数 3.2* 度 4.运用二叉树的…...

哈希表题目:猜数字游戏
文章目录题目标题和出处难度题目描述要求示例数据范围解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析题目 标题和出处 标题:猜数字游戏 出处:299. 猜数字游戏 难度 4 级 题目描述 要求 你在和朋友一起玩猜数字(Bulls…...
项目请求地址自动加上了本地ip的解决方式
一般情况下来说都是一些粗心大意的问题导致的 场景一:少加了/ 场景二:前后多加了空格 场景三:拼接地址错误
Vue3 企业级项目实战:项目须知与课程约定
本节内容很重要,希望大家能够耐心看完。 Vue3 企业级项目实战 - 程序员十三 - 掘金小册Vue3 Element Plus Spring Boot 企业级项目开发,升职加薪,快人一步。。「Vue3 企业级项目实战」由程序员十三撰写,2744人购买https://s.ju…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
