11.28~11.29基本二叉树的性质、定义、复习;排序算法;堆
完全二叉树(Complete Binary Tree)是一种特殊的二叉树结构,它具有以下特点:
- 所有的叶子节点都集中在树的最后两层;
- 最后一层的叶子节点都靠左排列;
- 除了最后一层,其他层的节点数都达到最大值。
满二叉树(Full Binary Tree),又称为真二叉树,是一种特殊的完全二叉树结构,它具有以下特点:
- 所有的叶子节点都在同一层;
- 每个非叶子节点都有两个子节点;
- 所有节点的子节点数都为0或2。
满二叉树是完全二叉树的一种特殊情况,每个非叶子节点都有两个子节点,而完全二叉树可以有一个或没有一个子节点。
树的定义,遍历,输入构建,一些递归复习(求叶子节点,数的高度)
ABC##DE#G##F###
5
第二次实验——二叉树中序遍历
ABD##FE###CG#H##I##
DBEFAGHCI
第十一周,后序+中序确定二叉树
树的性质
第二次实验的思考题

一棵非空二叉树,若后序遍历与中序遍历的序列相同,则该二叉树所有结点均无右孩子。
非空的二叉树一定满足:某结点若有左孩子,则其中序前驱一定没有右孩子。
二分查找法
二叉搜索树复习
寻找公共祖先
排序算法
第二次实验——快速排序的过程
5
4 5 3 2 1
输出
2 1 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
插入排序还是归并排序
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Insertion Sort
1 2 3 5 7 8 9 4 6 0
10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6
Merge Sort
1 2 3 8 4 5 7 9 0 6
插入排序,冒泡排序,选择排序,堆排序,归并排序
第八周习题——冒泡排序
第九周习题——二路归并排序
归并排序,逆序对
第七周——插入排序
结构体排序
第九周习题——成绩排名
第八周习题——小球装箱
排序算法性质
合并排序算法是稳定的排序方法。


直接插入排序在最好的情况下时间复杂度为O(n)

直接插入排序是稳定的
逆序对,倍数对
堆的调整,构建
调整
void shiftup(int child) {//在末尾插入一个孩子,然后就这个孩子一直往上调整,这样的话调整路径都满足堆的性质int parent = (child - 1) / 2;while (child > 0) {if (arr[parent] > arr[child]) {break;}else {swap(arr[parent], arr[child]);child = parent;//往上调整一步parent = (child - 1) / 2;//这里是先调整了孩子指针,所以这时候的父母就是父母的父母}}
}
void shiftup(int child) {int parent = (child - 1) / 2;while (child > 0) {if (arr[parent] > arr[child]) { break; }//大顶堆,上面大,就不调整了else {swap(arr[parent], arr[child]);child = parent;parent = (child - 1) / 2;}}
}
//向上调整的话就是找到最后一个孩子,然后找到它的父母节点,孩子对应的父母节点是唯一的,所以可以直接比较
//直接比较完后直接交换,直到到底
//向下调整的话就是先找到堆顶元素,然后由于堆是完全二叉树,所以对应两个孩子,找到最小的孩子,然后调整
//调整后,使被调整的孩子作为父母节点,找到其左孩子节点
//即,向上调整只需要找到一个节点信息,即当下节点信息,就可以确定父母节点,单向比较即可
//而向下调整需要两个节点信息,一个是当下节点信息(父母节点),还要直到它是否有孩子,默认为左孩子,然后判断一下有没有右孩子
//由此向下递归进行需要两个信息,一个父母节点,一个孩子节点,递归时默认孩子节点为左孩子,2*cur+1,然后尝试找右孩子
//如果在下次递归时,左孩子越界,那就说明此时父母节点已是叶子节点,到底了,无法继续调整。
void shiftdown(int[]arr, int size, int parent) {int child = parent * 2 + 1;while (child < size) {if (child + 1 < size && arr[child + 1] > arr[child]) {child += 1;}if (arr[parent] < arr[child]) {swap(arr, parent, child);parent = child;//由此,完成向下移动,child = parent * 2 + 1;//孩子与父母指针都向下移动}else {return;}}
}void shiftdown(int[]arr, int parent) {//父母直接,指向要交换的元素int child = 2 * parent + 1;//孩子指针,指向要交换的元素int size = arr.length();while (child < size) {//只要有这一步,就说明当下节点至少存在左孩子if (child + 1 < size && arr[child + 1] < arr[child]) {child += 1;//如果向右一个单位存在,就说明当下节点有右孩子,找最小的}//确定较小的孩子if (arr[parent] <= arr[child]) {break;}else {int t = arr[parent];parr[parent] = arr[child];arr[child] = t;parent = child;child = parent * 2 + 1;}}
}如果左孩子存在,则child<size,不断进行操作,直到左孩子不存在
检测右孩子是否存在,找左右孩子中最小的孩子
堆的创建
这个就是先输入,输入一个数组,输入完后再开始调整,从最后一个非叶子结点开始,然后不断往上往回走,进行向下调整
public static void createHeap(int[] array) {// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整for(int root = (array.length-2)/2; root >= 0; root--){shiftDown(array, array.length, root);}
}插入,边插边保持堆
int arr[100];
int siz = 0;
void shiftup(int child) {int parent = (child - 1) / 2;while (child > 0) {if (arr[parent] >= arr[child]) {break;}else {swap(arr[parent], arr[child]);child = parent;parent = (child - 1) / 2;}}
}
void insert(int num) {arr[siz++] = num;shiftup(siz - 1);
}二叉树指针关系
对于二叉树的孩子双亲指针指引,如果是从1开始记录的,那么
左孩子结点索引 = 2 * i 右孩子结点索引 = 2 * i + 1
其中,i表示当前结点的索引位置。
当索引从1开始记录时,根节点的索引为1,其左孩子结点的索引为2,而右孩子结点的索引为3。对于任意结点i,其左孩子结点的索引位置为2 * i,右孩子结点的索引位置为2 * i + 1。
如果是从0开始记录的,
二叉树以数组形式存储时,一般约定根节点的索引位置为0,其左孩子结点的索引位置为1,右孩子结点的索引位置为2。对于任意结点i,其左孩子结点的索引位置为2 * i + 1,右孩子结点的索引位置为2 * i + 2。
堆的一些性质
下标从0开始计数的堆,大小为size时,其最后一个非叶子结点是(size-2)/2;
最后一个叶子结点的下标为size-1.
由于是下标从0,所以对结点i而言,其双亲结点下标为(i-1)/2
(如果下标从1开始,那么整体往右偏移一位)
所以对于下标为size-1的结点,它的双亲结点为(size-1-1)/2;
最大堆(大顶堆、max-heap)从根结点到其它任一结点的路径上的所有结点值是从大到小排列的。

第十二周堆的操作,堆的建立
找第k小
相关文章:

11.28~11.29基本二叉树的性质、定义、复习;排序算法;堆
完全二叉树(Complete Binary Tree)是一种特殊的二叉树结构,它具有以下特点: 所有的叶子节点都集中在树的最后两层;最后一层的叶子节点都靠左排列;除了最后一层,其他层的节点数都达到最大值。 …...

轮播插件Slick.js使用方法详解
相比于Swiper而选择使用Slick.js的原因主要是因为其兼容不错并且在手机端的滑动效果更顺畅 参数: 1.基本使用:一般使用只需前十个属性 $(.box ul).slick({autoplay: true, //是否自动播放pauseOnHover: false, //鼠标悬停暂停自动播放speed: 1500, //…...

postgresql pg_hba.conf 配置详解
配置文件之pg_hba.conf介绍 该文件用于控制访问安全性,管理客户端对于PostgreSQL服务器的访问权限,内容包括:允许哪些用户连接到哪个数据库,允许哪些IP或者哪个网段的IP连接到本服务器,以及指定连接时使用的身份验证模…...
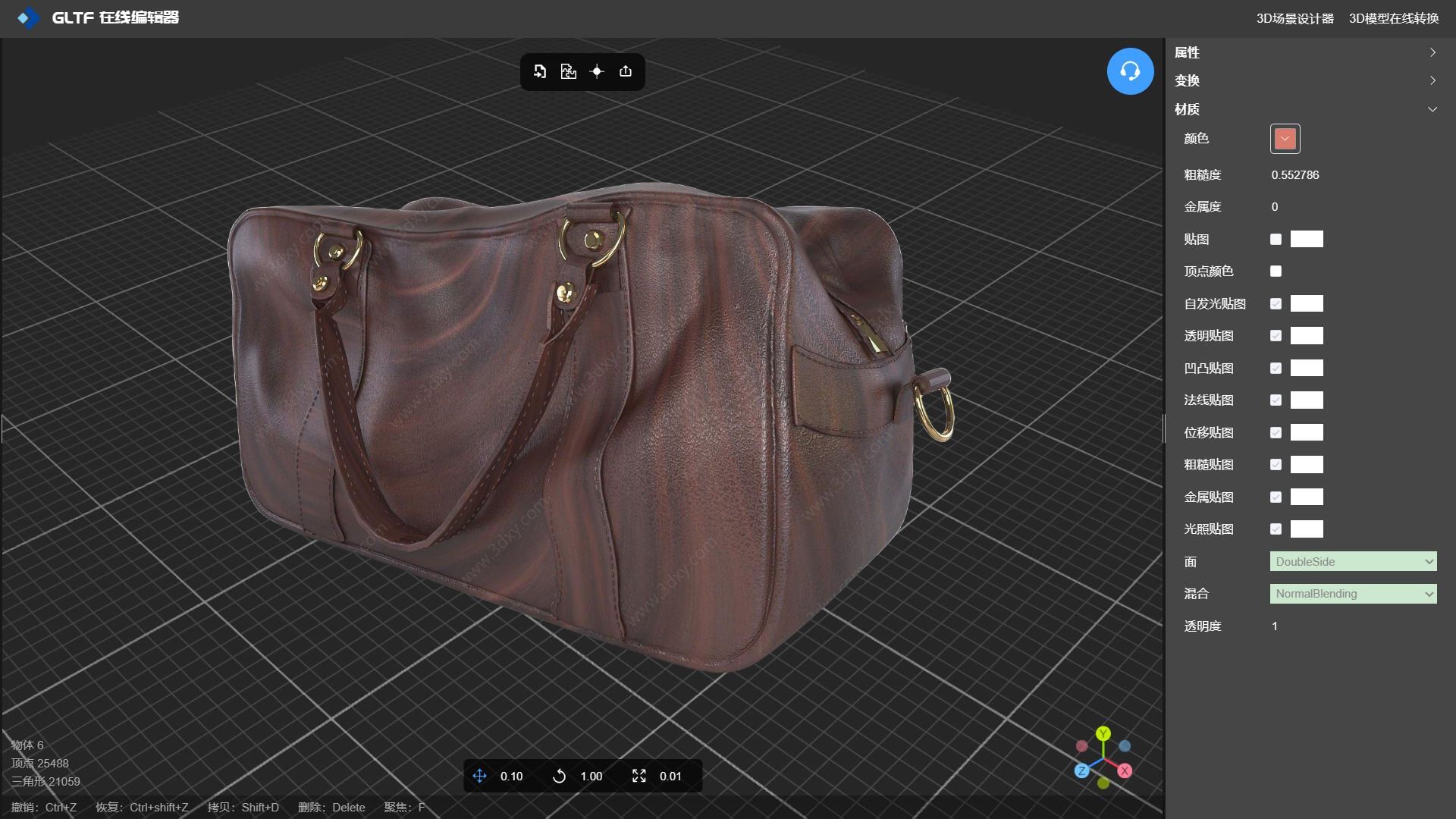
使用粗糙贴图制作粗纹皮革手提包3D模型
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理编辑器 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 当谈到游戏角色的3D模型风格时,有几种不同的风格…...
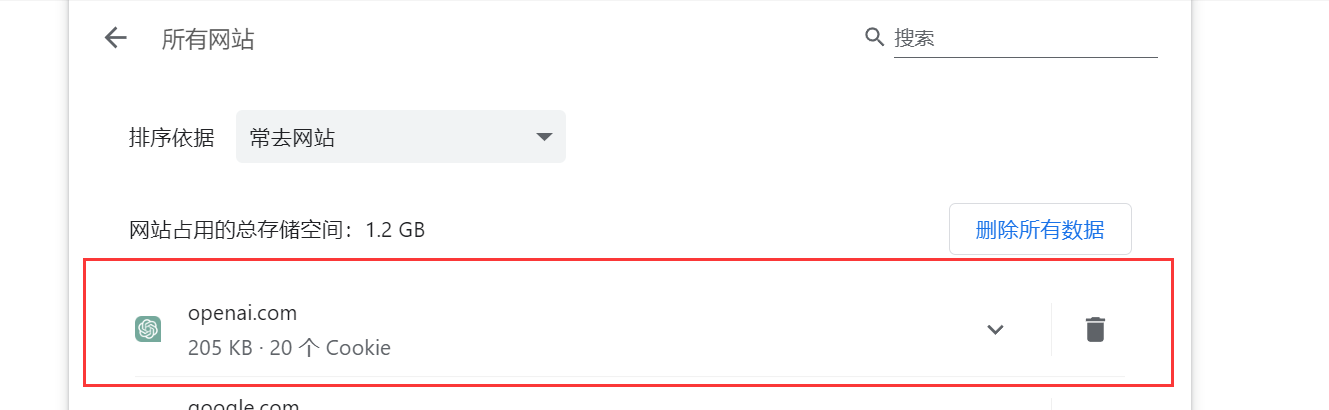
Chrome清除特定网站的Cookie,从而让网址能正常运行(例如GPT)
Chrome在使用某些网址的时候,例如GPT的时候,可能会出现无法访问这个网址的情况,就是点不动啥的 只需要把你需要重置的网址删除就好了...

history路由解决刷新出现404的问题
本文具体重点介绍怎么解决浏览器路由(history模式)解决404的问题。 在项目打包上线时,如果采用的是哈希模式,不会出现404,原因是 url 中 # 号后面的内容不会发给后端当作资源路径请求服务器。 具体流程(哈…...
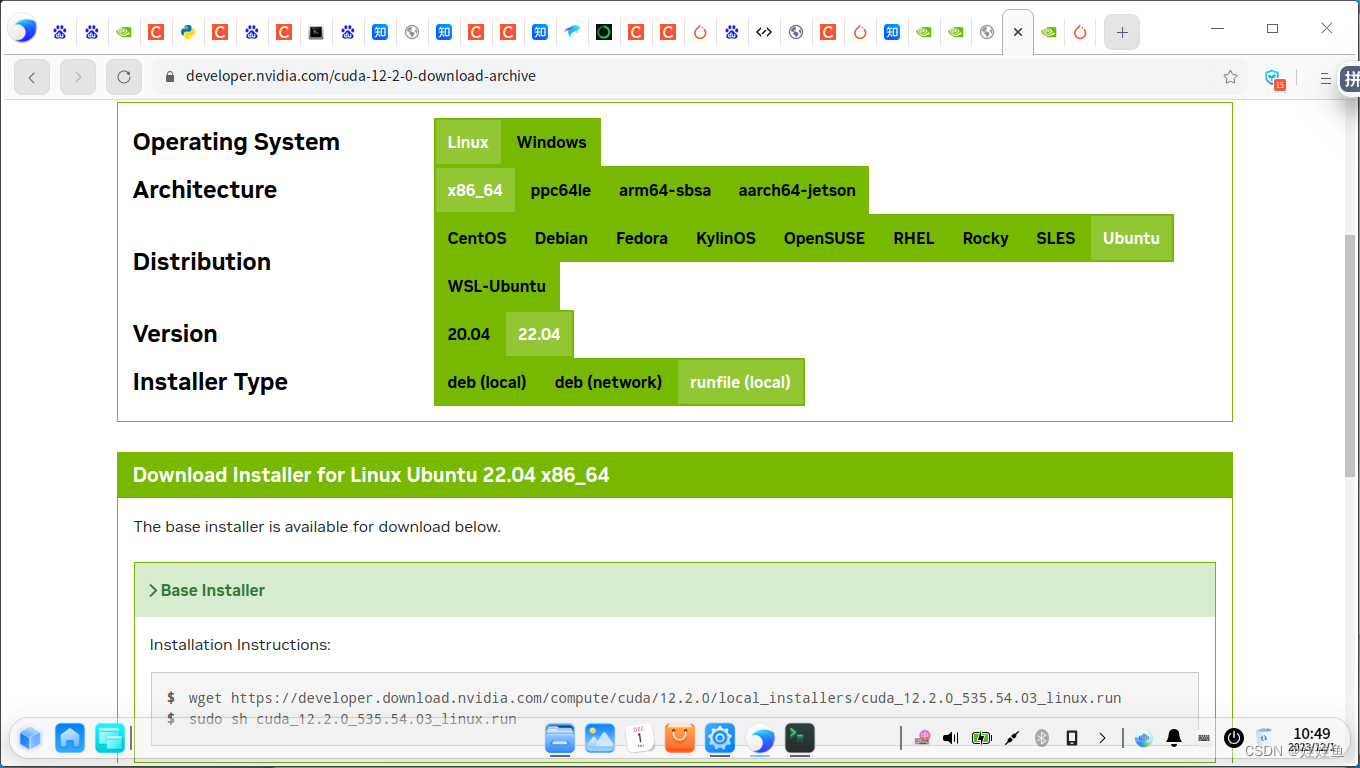
ubuntu22下使用nvidia 2080T显卡部署pytorch
1.直接到NVIDA官网下载相应的驱动,然后安装官方驱动 | NVIDIA 2.下载相应版本cuda,并安装,安装时不安装驱动 3.conda install pytorch2.1.0 torchvision0.16.0 torchaudio2.1.0 pytorch-cuda12.1 -c pytorch -c nvidia 安装pytorch。 安装…...

【Spark基础】-- 理解 Spark shuffle
目录 前言 1、什么是 Spark shuffle? 2、Spark 的三种 shuffle 实现 3、参考 前言 以前,Spark 有3种不同类型的 shuffle 实现。每种实现方式都有他们自己的优缺点。在我们理解 Spark shuffle 之前,需要先熟悉 Spark 的 execution model 和一些基础概念,如:MapReduce、…...
软件测试入门:静态测试
什么是静态测试 顾名思义,这里的静态是指程序的状态,即在不执行代码的情况下检查软件应用程序中的缺陷。进行静态测试是为了仅早在开发的早期阶段发现程序缺陷,因为这样可以更快速地识别缺陷并低成本解决缺陷,它还有助于查找动态测…...

力扣labuladong一刷day30天二叉树
力扣labuladong一刷day30天二叉树 文章目录 力扣labuladong一刷day30天二叉树一、654. 最大二叉树二、105. 从前序与中序遍历序列构造二叉树三、106. 从中序与后序遍历序列构造二叉树四、889. 根据前序和后序遍历构造二叉树 一、654. 最大二叉树 题目链接:https://…...

【云原生-K8s】检查yaml文件安全配置kubesec部署及使用
基础介绍基础描述特点 部署在线下载百度网盘下载安装 使用官网样例yamlHTTP远程调用安全建议 总结 基础介绍 基础描述 Kubesec 是一个开源项目,旨在为 Kubernetes 提供安全特性。它提供了一组工具和插件,用于保护和管理在 Kubernetes 集群中的工作负载和…...

LeetCode力扣每日一题(Java):20、有效的括号
一、题目 二、解题思路 1、我的思路 我看到题目之后,想着这可能是力扣里唯一一道我能秒杀的题目了 于是一波操作猛如虎写出了如下代码 public boolean isValid(String s) {char[] c s.toCharArray();for(int i0;i<c.length;i){switch (c[i]){case (:if(c[i]…...
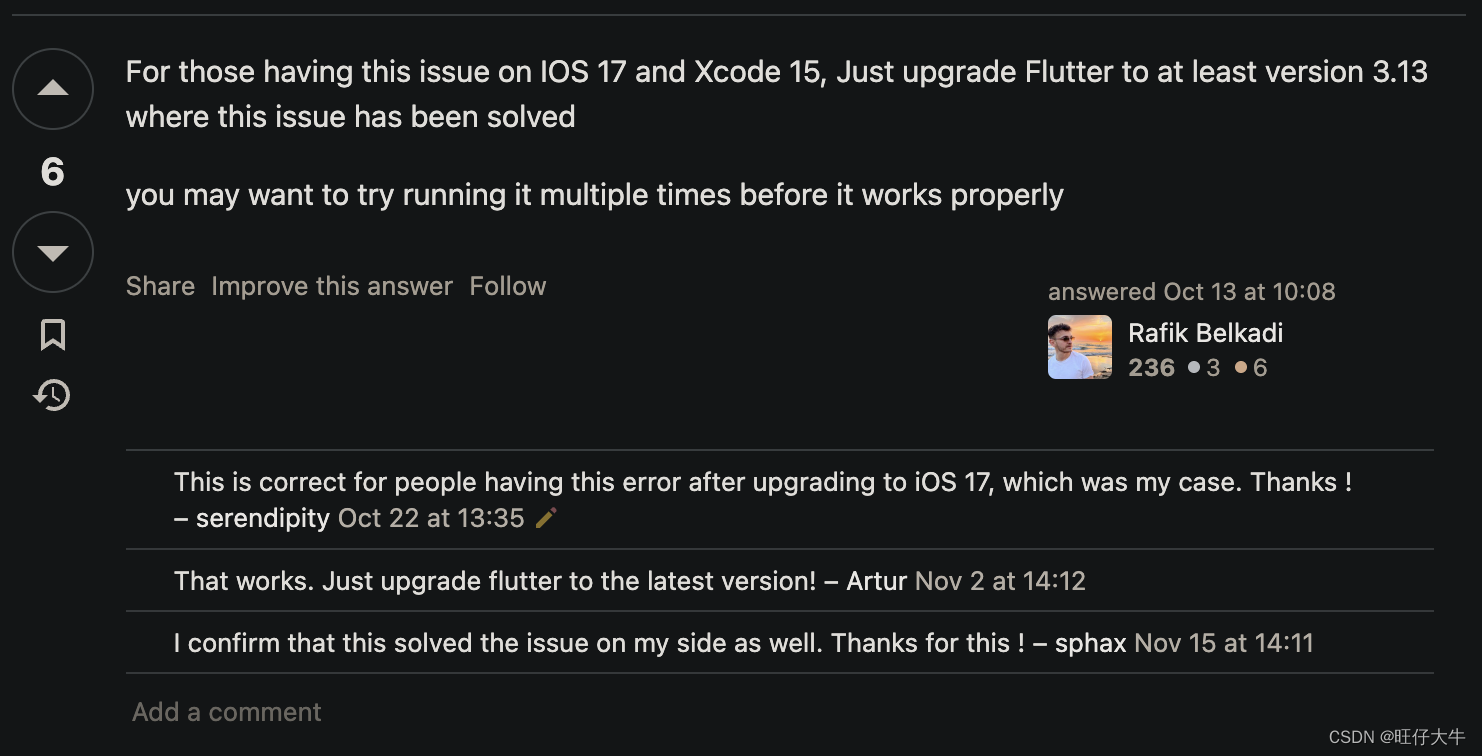
解决Flutter运行报错Could not run build/ios/iphoneos/Runner.app
错误场景 更新了IOS的系统版本为最新的17.0, 运行报以下错误 Launching lib/main.dart on iPhone in debug mode... Automatically signing iOS for device deployment using specified development team in Xcode project: GN3DCAF71C Running Xcode build... Xcode build d…...
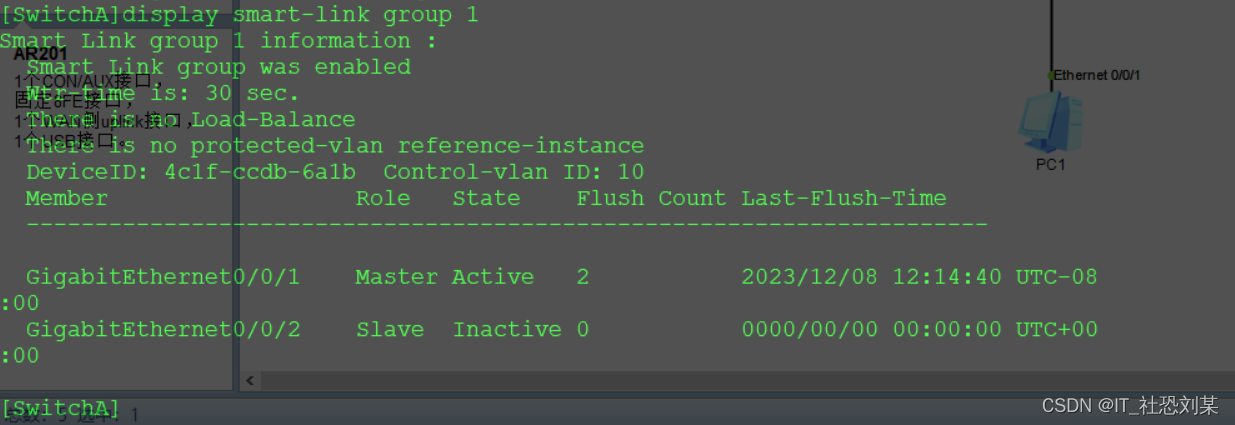
配置Smart Link主备备份示例
目录 实验拓扑 组网需求 配置思路 配置步骤 1.配置VLAN信息 2.在SwitchA上创建Smart Link备份组,并指定端口角色 3.使能回切功能并设置回切时间 4.使能发送Flush报文功能 5.使能接受Flush报文功能 验证配置结果 实验拓扑 组网需求 如上图所示,…...

03-微服务架构构建之微服务拆分
文章目录 前言一、微服务拆分的原则二、微服务拆分的时机三、微服务拆分的方法总结 前言 微服务架构是将一个单体应用程序拆分为一个个独立且保持松耦合的服务的一种架构方式,每个服务有着独立的数据库并且能独立运行部署。微服务架构的构建过程中,第一…...

Linus:我休假的时候也会带着电脑,否则会感觉很无聊
目录 Linux 内核最新版本动态 关于成为内核维护者 代码好写,人际关系难处理 内核维护者老龄化 内核中 Rust 的使用 关于 AI 的看法 参考 12.5-12.6 日,Linux 基金会组织的开源峰会(OSS,Open Source Summit)在日…...

快速排序的新用法
普通快排 简介 快速排序是一种高效的排序算法,利用分治的思想进行排序。它的基本原理是在待排序的n个数据中任取一个数据为分区标准,把所有小于该排序码的数据移到左边,把所有大于该排序码的数据移到右边,中间放所选记录&#x…...
利用乔拓云SAAS系统,快速、高效搭建小程序
a-service,软件即服务)系统来搭建他们的微信小程序。SAAS系统作为一种创新的软件应用模式,将软件作为一种服务提供给用户,为用户提供了更高效、更便捷的解决方案。本文将探讨为什么越来越多的商家选择使用乔拓云这种SAAS系统搭建小…...
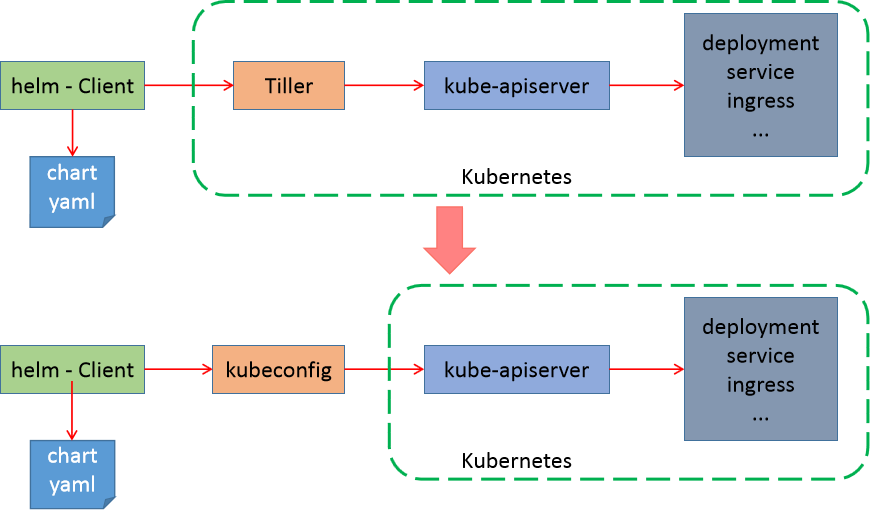
Kubernetes(K8s 1.27.x) 快速上手+实践,无废话纯享版
文章目录 1 基础知识1.1 K8s 有用么?1.2 K8s 是什么?1.3 k8s 部署方式1.4 k8s 环境解析 2 环境部署2.1 基础环境配置2.2 容器环境操作2.3 cri环境操作2.4 harbor仓库操作2.5 k8s集群初始化2.6 k8s环境收尾操作 3 应用部署3.1 应用管理解读3.2 应用部署实…...

非常抱歉的通知
非常感谢有这么多的同志向我提问一些问题,也非常感谢很多的同志可以看我的学习文章,这次大概有四五个月没有上csdn,看到了许多同志的疑问和慰问,我也很感动,但是由于我自己以及其他的原因,我现在打算以考编…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
